(完整word)线面平行垂直知识点,推荐文档
- 格式:doc
- 大小:130.35 KB
- 文档页数:8
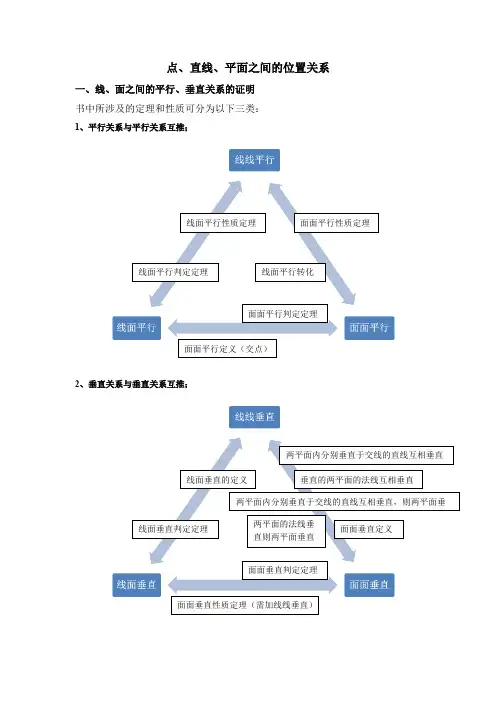
点、直线、平面之间的位置关系一、线、面之间的平行、垂直关系的证明书中所涉及的定理和性质可分为以下三类:1、平行关系与平行关系互推;2、垂直关系与垂直关系互推;线面垂直判定定理线面垂直的定义两平面的法线垂直则两平面垂直面面垂直判定定理线面平行判定定理线面平行性质定理线面平行转化面面平行判定定理面面平行性质定理3、平行关系与垂直关系互推。
以线或面为元素,互推的本质是以某一元素为中介,通过另外两元素与中介元素的垂直或平行关系,推导出该两元素的关系,总共有21种情况,能得出结论的有以下9种情况。
线线平行传递性:;b c c a b a //////⇒⎭⎬⎫面面平行传递性:;γαβγβα//////⇒⎭⎬⎫线面垂直、线面垂直线面平行:;⇒ααββα//a a a ⇒⎪⎭⎪⎬⎫⊄⊥⊥线面垂直线线平行(线面垂直性质定理):;⇒b a b a //⇒⎭⎬⎫⊥⊥αα线面垂直面面平行:;⇒βαβα//⇒⎭⎬⎫⊥⊥a a 线面垂直、面面平行线面垂直:;⇒βαβα⊥⇒⎭⎬⎫⊥a a //线线平行、线面垂直线面垂直:;⇒αα⊥⇒⎭⎬⎫⊥b a b a //线面垂直、线面平行面面垂直:。
⇒βααβ⊥⇒⎭⎬⎫⊥a a //备注:另外证明平行关系时可以从最基本的定义交点入手,证明垂直关系时可以从最基本的定义角度入手。
符号化语言一览表①线面平行;;;ααα////a a b b a ⇒⎪⎭⎪⎬⎫⊄⊂αββα////a a ⇒⎭⎬⎫⊂ααββα//a a a ⇒⎪⎭⎪⎬⎫⊄⊥⊥②线线平行:;;;;////a a a b b αβαβ⎫⎪⊂⇒⎬⎪=⎭ b a b a //⇒⎭⎬⎫⊥⊥αα////a a b b αβαγβγ⎫⎪=⇒⎬⎪=⎭b c c a b a //////⇒⎭⎬⎫③面面平行:;;;,////,//a b a b O a b αααβββ⊂⊂⎫⎪=⇒⎬⎪⎭βαβα//⇒⎭⎬⎫⊥⊥a a γαβγβα//////⇒⎭⎬⎫④线线垂直:;b a b a ⊥⇒⎭⎬⎫⊂⊥αα⑤线面垂直:;;,,a b a b O l l a l b ααα⊂⊂⎫⎪=⇒⊥⎬⎪⊥⊥⎭,l a a a l αβαββα⊥⎫⎪=⇒⊥⎬⎪⊂⊥⎭ ;;βαβα⊥⇒⎭⎬⎫⊥a a //αα⊥⇒⎭⎬⎫⊥b a b a //⑥面面垂直:二面角900; ;;βααβ⊥⇒⎭⎬⎫⊥⊂a a βααβ⊥⇒⎭⎬⎫⊥a a //二、立体几何中的重要方法1、求角:(步骤-------Ⅰ找或作角;Ⅱ求角)⑴异面直线所成角的求法:①平移法:平移直线,构造三角形;②补形法:补成正方体、平行六面体、长方体等,发现两条异面直线间的关系.注:还可用向量法,转化为两直线方向向量的夹角.⑵直线与平面所成的角:①直接法(利用线面角定义);②先求斜线上的点到平面距离h ,与斜线段长度作比,得sin ;③三线三角公式.θ12cos cos cos θθθ=注:还可用向量法,转化为直线的方向向量与平面法向量的夹角.⑶二面角的求法:①定义法:在二面角的棱上取一点(特殊点),作出平面角,再求解;②垂面法:作面与二面角的棱垂直; ③投影法(三垂线定理);④面积摄影法.注:对于没有给出棱的二面角,应先作出棱,然后再选用上述方法;还可用向量法,转化为两个班平面法向量的夹角.2、求距离:(步骤-------Ⅰ找或作垂线段;Ⅱ求距离)⑴两异面直线间的距离:一般先作出公垂线段,再进行计算;或转化为线面距离、点面距离;⑵点到直线的距离:一般用三垂线定理作出垂线段,再求解;⑶点到平面的距离:①垂面法:借助面面垂直的性质作垂线段(确定已知面的垂面是关键),再求解;②等体积法;还可用向量法:.||n d =3、证明平行、垂直的理论途径:①证明直线与直线的平行的思考途径:(1)转化为判定共面二直线无交点(定义);(2)转化为两直线同与第三条直线平行;(3)转化为线面平行;(4)转化为线面垂直;(5)转化为面面平行.②证明直线与平面的平行的思考途径:(1)转化为直线与平面无公共点(定义);(2)转化为线线平行;(3)转化为面面平行.③证明平面与平面平行的思考途径:(1)转化为判定两平面无公共点(定义);(2)转化为线面平行;(3)转化为线面垂直.④证明直线与直线的垂直的思考途径:(1)转化为相交垂直;(2)转化为线面垂直.⑤证明直线与平面垂直的思考途径:(1)转化为该直线与平面内任一直线垂直(定义);(2)转化为该直线与平面内相交的两条直线垂直;(3)转化为该直线与平面的一条垂线平行;(4)转化为该直线垂直于另一个平行平面;(5)转化为该直线与两个垂直平面交线垂直.⑥证明平面与平面的垂直的思考途径:(1)转化为判断二面角是直二面角;(2)转化为线面垂直.。

2.3.1 直线与平面垂直的判定2.3.2 平面与平面垂直的判定学习目标:1、 掌握直线与平面垂直的定义及判定定理;2、 掌握直线、平面垂直的文字,符号,图形语言之间的相互转化;3、 掌握平面与平面垂直的定义,理解二面角,二面角的平面角的定义;4、 掌握平面与平面垂直的判定预习导引:1、要点扫描:1、直线与平面垂直(1)定义:如果直线l 与平面α内的_______直线都________。
我们就说直线l 与平面α垂直,记作________。
直线l 叫做平面α的_________。
平面α叫做直线l 的_______。
直线与平面垂直时,它们唯一的公共点P 叫做_________。
(2)画法:通常把直线画成与表示平面的平行四边形的一边垂直。
(3)判定定理文字表述:一条直线与一个平面内的_______都垂直,则该直线与此平面垂直。
符号表述:,l a l b ⊥⊥,_______,__________⇒l α⊥.2、直线与平面所成的角(1)定义:平面的一条射线和它在平面上的______所成的______,叫做这条直线和这个二平面所成的角。
(2)当直线与平面垂直时,它们所成的角是_______。
(3)当直线与平面平行或者在平面内时,它们所成的角是_______。
(4)线面角的取值范围:_________。
3、(1)二面角:从一条直线出发的两个半平面所成的________叫做二面角。
这条直线叫做二面角的_________,这两个半平面叫做二面角的____________。
(2)、二面角的平面角: 定义:如图,二面角D-AB-F 。
若有H___AB ,HI___面ABCD ,HG___面ABFE ,HG___AB,HI____AB ,则角GHI 就叫做二面角D-AB-F 的平面角。
范围:00[0,180]当二面角的两个半平面重合时所成角为00当两个半平面组成一个平面时,所成角为0180(3)、平面与平面的垂直 定义:一般地,如果两个平面相交,且他们所成的二面角是_______,就说这两个平面互相垂直。

线面、面面平行和垂直的八大定理一、线面平行。
1、判断定理:平面外一条直线与平面内一条直线平行,那么这条直线与这个平ab a //面平行。
切合表示: a // b2、性质定理:假如一条直线与平面平行,经过这条直线的平面和这个平面订交,那么这条直线和交线平行。
符号表示:aa //a // bab二、面面平行。
1、判断定理:假如一个平面内有两条订交直线分别平行于另一个平面内的两条订交直线,那么这两个平面平行。
n // bm // aa b M//m n N符号表示:2、性质定理:假如两个平面平行同时与第三个平面订交,那它们的交线平行。
//符号表示:l l // d (更为适用的性质:一个平d面内的任向来线平行另一平面)三、线面垂直。
1、判断定理:假如一条直线与一个平面内的两条订交直线都垂直,那么这条直a c线垂直这个平面。
a b符号表示:ab c M$:三垂线定理:(常常考到这类逻辑)在平面内的一条直线,假如它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
符号表示:aoAa PApoa oA A2、性质定理:垂直同一平面的两条直线相互平行。
(更为适用的性质是:一个平面的垂线垂直于该平面内任向来线。
)四、面面垂直。
1、判断定理:经过一个平面的垂线的平面与该平面垂直。
a, a2、性质定理:已知两个平面垂直,在一个平面内垂直于交线的直线垂直于另一个平面。
,b, a, a b a。

线面平行知识点总结一、线面平行的定义1. 线面平行是指在三维空间中,两条直线或者一个直线与一个平面的关系。
如果两条直线在同一个平面上且不相交,则它们是线面平行的;如果一条直线与一个平面平行,则它们是线面平行的。
2. 线面平行的判断方法:- 根据定义,两条直线在同一个平面上且不相交即为线线平行,可以通过观察二维平面投影来进行判断;- 通过向量的性质来判断,如果两条直线在同一个平面上且它们的方向向量平行,则它们是线线平行的;- 对于线面平行,直线的方向向量与平面的法向量平行。
3. 线面平行的特点:- 对于线线平行,它们在同一个平面上且不相交;- 对于线面平行,直线的方向向量与平面的法向量平行。
二、线面平行的应用1. 几何形状的判断- 在空间几何中,线面平行的概念常常用于判断几何形状的性质。
例如,在判断一个立方体的对角线是否在同一个平面上时,就可以利用线面平行的性质来进行推理。
2. 建模与设计- 在工程建模和设计中,线面平行的概念也有着重要的应用。
例如在建筑设计中,为了保证构件的安装与连接,需要考虑构件之间的线面平行关系,以确保各构件之间的准确配合。
三、线面平行的相关定理1. 平行线性质定理- 定理1:两条直线在同一个平面上且平行,则它们的方向向量成比例;- 定理2:如果一条直线与一个平面平行,则直线上的任意一点到平面的距离等于这个点到平面的法向量的点积的绝对值。
2. 平面平行性质定理- 定理1:如果两个平行的平面被交叉一条直线所截,则它们的法向量成比例;- 定理2:如果两个平面平行,那么它们的法向量成比例,且它们之间的距离是相等的。
3. 线面平行的性质定理- 定理1:如果一条直线与一个平面平行,则直线上的任意一点到平面的距离等于这个点到平面的法向量的点积的绝对值;- 定理2:如果一条直线与一个平面平行,并且与这个平面内的直线相交,则这两条直线的夹角等于直线的方向向量与平面的法向量的夹角。
四、线面平行的相关问题1. 直线在平面内的投影问题- 给定一个直线和一个平面,在平面上求直线的投影。

线面平行垂直知识点一、线面平行的定义和性质1.定义:线面平行是指一条直线与一个平面内的所有直线都不相交。
2.性质:a.对于一个平面内的一条直线和平面外的任意一条直线,它们都不能同时与该平面平行。
b.平行线与同一平面内的另一条直线的关系:如果两条直线都与同一个平面平行,则这两条直线要么相交,要么重合。
c.平行线与不同平面内的直线的关系:如果两条直线分别与两个不相交平面平行,则这两条直线不相交。
二、线面垂直的定义和性质1.定义:线面垂直是指一条直线与一个平面内的所有直线都垂直相交。
2.性质:a.如果一条直线与一个平面垂直,则这条直线与平面内的任意一条直线都垂直。
b.平行于同一个平面内的两条直线不存在垂直关系。
c.如果两个平面垂直,则其法线向量互相垂直。
三、线面平行和垂直的判定方法1.平行判定:线面平行的判定可以通过向量的方法、斜率的方法和直线与平面的交点判定方法等。
例如,若两个平面的法线向量相等或平行,则这两个平面是平行的。
2.垂直判定:线面垂直的判定可以通过两条直线的方向向量相互垂直、用点法式判断直线与平面之间的关系等方法。
例如,若一条直线与一个平面垂直,则这条直线的方向向量与该平面的法线向量垂直。
四、线面平行和垂直的应用1.线面平行和垂直的知识可以用于建筑设计中,例如判断条墙与地面是否平行或垂直,从而影响建筑的结构布局。
2.在工程测量中,线面平行和垂直关系的知识可以用于量测一些平面的倾斜度和水平度等参数。
3.在图形的投影与透视等绘图问题中,线面平行和垂直关系的知识可以帮助我们正确地绘制出图形的形状和位置。
综上所述,线面平行和垂直是几何学中非常重要的概念,其涉及到线与面之间的相互关系。
了解线面平行和垂直的定义、性质以及判定方法,可以帮助我们更好地理解空间几何中的问题,并应用于实际生活和工作中。

期末复习直线、平面垂直的判定和性质班级:姓名:一.知识点梳理考点一直线与平面平行的判定定理和性质定理考点二平面与平面平行的判定定理和性质定理(1)垂直于同一条直线的两个平面平行,即若a⊥α,a⊥β,则α⊥β.(2)垂直于同一个平面的两条直线平行,即若a⊥α,b⊥α,则a⊥b.(3)夹在两个平行平面之间的平行线段长度相等.(4)经过平面外一点有且只有一个平面与已知平面平行.(5)两条直线被三个平行平面所截,截得的对应线段成比例.(6)如果两个平面分别平行于第三个平面,那么这两个平面互相平行.(7)如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,那么这两个平面平行.二.常见题型题型一线面平行的判定与性质【题型要点】判断或证明线面平行的常用方法(1)利用线面平行的定义(无公共点).(2)利用线面平行的判定定理(a⊥α,b⊥α,a⊥b⊥a⊥α).(3)利用面面平行的性质定理(α⊥β,a⊥α⊥a⊥β).(4)利用面面平行的性质(α⊥β,a⊥α,a⊥β,a⊥α⊥a⊥β).类型一直线与平面平行的判定典例1 如图所示,斜三棱柱ABCA1B1C1中,点D,D1分别为AC,A1C1的中点.(1)证明:AD1⊥平面BDC1;(2)证明:BD⊥平面AB1D1.【证明】(1)因为D1,D分别为A1C1,AC的中点,四边形ACC1A1为平行四边形,所以C1D1綊DA,所以四边形ADC1D1为平行四边形,所以AD1⊥C1D,又AD1⊥平面BDC1,C1D⊥平面BDC1,所以AD1⊥平面BDC1.(2)连接D1D,因为BB1⊥平面ACC1A1,BB1⊥平面BB1D1D,平面ACC1A1∩平面BB1D1D=D1D,所以BB1⊥D1D,又因为D 1,D分别为A1C1,AC的中点,所以DD1綊AA1,所以BB1=AA1=DD1,故四边形BDD1B1为平行四边形,所以BD⊥B1D1,又BD⊥平面AB1D1,B1D1⊥平面AB1D1,所以BD⊥平面AB1D1.类型二直线与平面平行的性质典例2 如图,四棱锥PABCD的底面是边长为8的正方形,四条侧棱长均为217,点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC⊥平面GEFH.(1)证明:GH⊥EF;(2)若EB=2,求四边形GEFH的面积.(1)证明:因为BC⊥平面GEFH,BC⊥平面PBC,且平面PBC∩平面GEFH=GH,所以GH⊥BC.同理可证EF⊥BC,因此GH ⊥EF .(2)连接AC ,BD 交于点O ,BD 交EF 于点K ,连接OP ,GK .因为P A =PC ,O 是AC 的中点,所以PO ⊥AC ,同理可得PO ⊥BD .又BD ∩AC =O ,且AC ,BD 都在底面ABCD 内,所以PO ⊥底面ABCD .又因为平面GEFH ⊥平面ABCD ,且PO ⊥平面GEFH ,所以PO ⊥平面GEFH .因为平面PBD ∩平面GEFH =GK ,所以PO ⊥GK ,所以GK ⊥底面ABCD ,从而GK ⊥EF .所以GK 是梯形GEFH 的高.由AB =8,EB =2得EB ⊥AB =KB ⊥DB =1⊥4,从而KB =14DB =12OB ,即K 为OB 的中点. 再由PO ⊥GK 得GK =12PO ,且G 是PB 的中点,所以GH =12BC =4. 由已知可得OB =42,PO =PB 2-OB 2=68-32=6,所以GK =3.易得EF =BC =8,故四边形GEFH 的面积S =GH +EF 2·GK =4+82×3=18. 典例3 (1)(福建省龙岩一中2019届期末)若直线l 不平行于平面α,且l ⊄α,则( )A.α内的所有直线与l 异面B.α内不存在与l 平行的直线C.α与直线l 至少有两个公共点D.α内的直线与l 都相交【答案】B【解析】因为l ⊄α,直线l 不平行于平面α,所以直线l 只能与平面α相交,于是直线l 与平面α只有一个公共点,所以平面α内不存在与l 平行的直线.(2).(云南省曲靖一中2019届期末)如图所示的三棱柱ABC -A 1B 1C 1中,过A 1B 1的平面与平面ABC 交于DE ,则DE 与AB 的位置关系是( )A.异面B.平行C.相交D.以上均有可能【答案】B【解析】在三棱柱ABC -A 1B 1C 1中,AB ∥A 1B 1,∵AB ⊂平面ABC ,A 1B 1⊄平面ABC ,∴A 1B 1∥平面ABC ,∵过A 1B 1的平面与平面ABC 交于DE .∴DE ∥A 1B 1,∴DE ∥AB . 题型二 面面平行的判定与性质【题型要点】证明面面平行的常用方法(1)利用面面平行的定义.(2)利用面面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(3)利用“垂直于同一条直线的两个平面平行”.(4)利用“如果两个平面同时平行于第三个平面,那么这两个平面平行”.(5)利用“线线平行”“线面平行”“面面平行”的相互转化.典例4 如图所示,在三棱柱ABCA1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:(1)B,C,H,G四点共面;(2)平面EF A1⊥平面BCHG.【证明】(1)⊥G,H分别是A1B1,A1C1的中点,⊥GH是⊥A1B1C1的中位线,GH⊥B1C1.又⊥B1C1⊥BC,⊥GH⊥BC,⊥B,C,H,G四点共面.(2)在⊥ABC中,E,F分别为AB,AC的中点,⊥EF⊥B C.⊥EF⊥平面BCHG,BC⊥平面BCHG,⊥EF⊥平面BCHG.⊥A1G綊EB,⊥四边形A1EBG是平行四边形,则A1E⊥G B.⊥A1E⊥平面BCHG,GB⊥平面BCHG,⊥A1E⊥平面BCHG.⊥A1E∩EF=E,⊥平面EF A1⊥平面BCHG.典例5 如图,在正方体ABCDA1B1C1D1中,S是B1D1的中点,E,F,G分别是BC,DC,SC的中点,求证:(1)直线EG⊥平面BDD1B1;(2)平面EFG⊥平面BDD1B1.【证明】:(1)如图,连接SB,因为E,G分别是BC,SC的中点,所以EG⊥SB.又因为SB⊥平面BDD1B1,EG⊥平面BDD1B1,所以直线EG⊥平面BDD1B1.(2)连接SD,因为F,G分别是DC,SC的中点,所以FG⊥SD.又因为SD ⊥平面BDD 1B 1,FG ⊥平面BDD 1B 1,所以FG ⊥平面BDD 1B 1,又EG ⊥平面EFG ,FG ⊥平面EFG ,EG ∩FG =G ,所以平面EFG ⊥平面BDD 1B 1.题型三 平行关系中的探索性问题【题型要点】解决探索性问题的方法(1)根据探索性问题的设问,假设其存在并探索出结论,然后在这个假设下进行推理论证,若得到合乎情理的结论就肯定假设,若得到矛盾就否定假设.(2)按类似于分析法的格式书写步骤:从结论出发“要使……成立”“只需使……成立”.典例6 如图,四棱锥E ABCD ,平面ABCD ⊥平面ABE ,四边形ABCD 为矩形,AD =6,AB =5,BE =3,F 为CE 上的点,且BF ⊥平面ACE .(1)求证:AE ⊥BE ;(2)设M 在线段DE 上,且满足EM =2MD ,试在线段AB 上确定一点N ,使得MN ⊥平面BCE ,并求MN 的长.(1)证明:因为四边形ABCD 为矩形,所以BC ⊥AB .因为平面ABCD ⊥平面ABE ,平面ABCD ∩平面ABE =AB ,且BC ⊥平面ABCD ,所以BC ⊥平面ABE . 又AE ⊥平面ABE ,所以BC ⊥AE .因为BF ⊥平面ACE ,AE ⊥平面ACE ,所以BF ⊥AE .又因为BC ∩BF =B ,BC ⊥平面BCE ,BF ⊥平面BCE ,所以AE ⊥平面BCE ,因为BE ⊥平面BCE ,所以AE ⊥BE .(2)法一:如图,在⊥ADE 中过M 点作MG ⊥AD 交AE 于G 点,在⊥ABE 中过G 点作GN ⊥BE 交AB 于N 点,连接MN ,因为NG ⊥BE ,NG ⊥平面BCE ,BE ⊥平面BCE ,所以NG ⊥平面BCE .同理可证,GM ⊥平面BCE .因为MG ∩GN =G ,所以平面MGN ⊥平面BCE ,又因为MN ⊥平面MGN ,所以MN ⊥平面BCE ,因为N 点为线段AB 上靠近A 点的一个三等分点,AD =6,AB =5,BE =3,所以MG =23AD =4,NG =13BE =1,所以MN =MG 2+NG 2=42+12=17.法二:如图,过M 点作MG ⊥CD 交CE 于G 点,连接BG ,在AB 上取N 点,使得BN =MG ,连接MN , 因为MG ⊥CD ,EM =2MD ,所以MG =23CD , 因为AB ⊥CD ,BN =MG ,所以四边形MGBN 是平行四边形,所以MN ⊥BG ,又因为MN ⊥平面BCE ,BG ⊥平面BCE ,所以MN ⊥平面BCE ,又MG =23CD ,MG =BN ,所以BN =23AB , 所以N 点为线段AB 上靠近A 点的一个三等分点.在⊥CBG 中,因为BC =AD =6,CG =13CE =1362+32=5,cos⊥BCG =255, 所以BG 2=36+5-2×6×5×255=17, 所以MN =BG =17.典例7 如图,已知斜三棱柱ABC A 1B 1C 1中,点D ,D 1分别为AC ,A 1C 1上的点.(1)当A 1D 1D 1C 1等于何值时,BC 1⊥平面AB 1D 1? (2)若平面BC 1D ⊥平面AB 1D 1,求AD DC的值. 【答案】见解析【解析】(1)如图,取D 1为线段A 1C 1的中点,此时A 1D 1D 1C 1=1, 连接A 1B 交AB 1于点O ,连接OD 1.由棱柱的性质,知四边形A 1ABB 1为平行四边形,所以点O 为A 1B 的中点.在⊥A 1BC 1中,点O ,D 1分别为A 1B ,A 1C 1的中点,所以OD 1⊥BC 1.又因为OD 1⊥平面AB 1D 1,BC 1⊥平面AB 1D 1,所以BC 1⊥平面AB 1D 1.所以当A 1D 1D 1C 1=1时,BC 1⊥平面AB 1D 1. (2)由已知,平面BC 1D ⊥平面AB 1D 1,且平面A 1BC 1∩平面BDC 1=BC 1,平面A 1BC 1∩平面AB 1D 1=D 1O .因此BC 1⊥D 1O ,同理AD 1⊥DC 1.因为A 1D 1D 1C 1=A 1O OB ,A 1D 1D 1C 1=DC AD. 又因为A 1O OB =1,所以DC AD =1,即AD DC=1.。
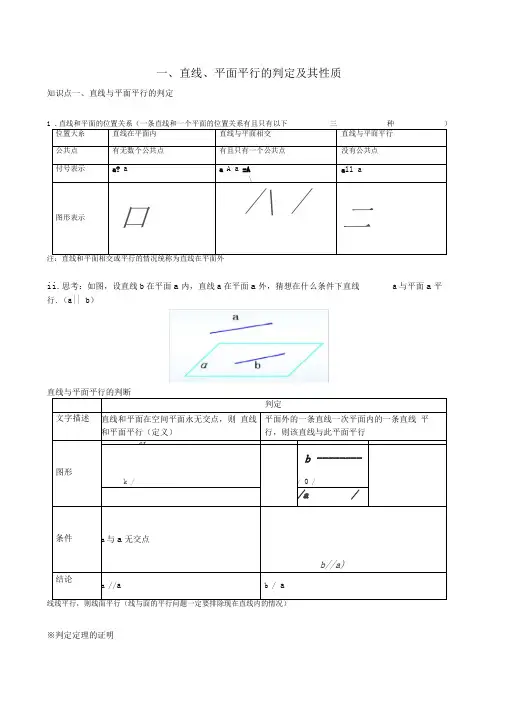
一、直线、平面平行的判定及其性质
知识点一、直线与平面平行的判定
ii.思考:如图,设直线b在平面a内,直线a在平面a外,猜想在什么条件下直线a与平面a平行.(a|| b)
直线与平面平行的判断
※判定定理的证明
特别提示
证明直线和平面的平行通常采用如下两种方法:①利用直线和平面平行的判定定理,通过“线线”平行,证得“线面”平行;②利用两平面平行的性质定理,通过“面面”平行,证得“线面”平行
、直线、平面垂直的判定及其性质知识点一、直线和平面垂直的定义与判定
要点诠释:定义中“平面
条直线”不同(线线垂直内的任意一条直线”就是
指“平面内的所有直线”,这与“无数
线面垂直)
知识点二、二面角
I.二面角::从一条直线出发的两个半平面所组成的图形叫二面角( dihedral angle ).这条直线叫做
二面角的棱,这两个半平面叫做二面角的面.记作二面角一AB —.(简记P — AB —Q)
.面角的平面角的三个特征:i .点在棱上
ii .线在面内
iii . 与棱垂直
n .二面角的平面角:在二面角一丨一的棱|上任取一点0,以点0为垂足,在半平面,内分别作垂直于棱I的射线0A和0B,则射线0A和0B构成的A0B叫做二面角的平面角.
作用:衡量二面角的大小;范围:0°180°.。

数学线面垂直的知识点总结归纳数学是一座高山,哪怕是高考数学这样的小山丘,也让无数学子望其背而心戚戚,更有人混淆知识点。
下面是小编为大家整理的关于数学线面垂直的知识点,希望对您有所帮助!数学直线与平面平行、垂直知识点直线与平面垂直的判定定理一:如果一条直线和一个平面内的两条相交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直,线面垂直”)直线与平面垂直的判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面.推论:如果两条直线同垂直于一个平面,那么这两条直线平行.注:①垂直于同一平面的两个平面平行.(×)(可能相交,垂直于同一条直线的两个平面平行)②垂直于同一直线的两个平面平行.(√)(一条直线垂直于平行的一个平面,必垂直于另一个平面)③垂直于同一平面的两条直线平行.(√)5. ⑴垂线段和斜线段长定理:从平面外一点向这个平面所引的垂线段和斜线段中,①射影相等的两条斜线段相等,射影较长的斜线段较长;②相等的斜线段的射影相等,较长的斜线段射影较长;③垂线段比任何一条斜线段短.注:垂线在平面的射影为一个点. [一条直线在平面内的射影是一条直线.(×)]⑵射影定理推论:如果一个角所在平面外一点到角的两边的距离相等,那么这点在平面内的射影在这个角的平分线上高中数学线面垂直知识点1)直线垂直于平面内两条非平行的线,则直线垂直于该平面2)直线的两条不平行的垂线与平面平行,则直线垂直于该平面3)有A、B两个面都与C平面垂直,则A、B两个面的交线也垂直于C平面4)直线垂直于与A平面平行的B平面,则直线垂直于A平面5)直线任意点在平面上的投影都重合,则直线垂直于该平面6)直线上任意点到平面的距离,都等于这一点到线面交点的距离,则直线垂直于该平面线面垂直性质定理1:如果一条直线垂直于一个平面,那么该直线垂直于平面内的所有直线。
2:经过空间内一点,有且只有一条直线垂直已知平面。


【精品文档】直线与平面平行、垂直有关知识点-精选word文档本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!== 本文为word格式,下载后可方便编辑和修改! ==直线与平面平行、垂直有关知识点直线与平面平行、直线与平面垂直.1. 空间直线与平面位置分三种:相交、平行、在平面内.2. 直线与平面平行判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行,线面平行”)[注]:①直线与平面内一条直线平行,则∥ . (×)(平面外一条直线)②直线与平面内一条直线相交,则与平面相交. (×)(平面外一条直线)③若直线与平面平行,则内必存在无数条直线与平行. (√)(不是任意一条直线,可利用平行的传递性证之)④两条平行线中一条平行于一个平面,那么另一条也平行于这个平面. (×)(可能在此平面内)⑤平行于同一直线的两个平面平行.(×)(两个平面可能相交)⑥平行于同一个平面的两直线平行.(×)(两直线可能相交或者异面)⑦直线与平面、所成角相等,则∥ .(×)(、可能相交)3. 直线和平面平行性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.(“线面平行,线线平行”)4. 直线与平面垂直是指直线与平面任何一条直线垂直,过一点有且只有一条直线和一个平面垂直,过一点有且只有一个平面和一条直线垂直.若⊥ ,⊥ ,得⊥ (三垂线定理),得不出⊥ . 因为⊥ ,但不垂直OA.三垂线定理的逆定理亦成立.直线与平面垂直的判定定理一:如果一条直线和一个平面内的两条相交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直,线面垂直”)直线与平面垂直的判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面.推论:如果两条直线同垂直于一个平面,那么这两条直线平行.[注]:①垂直于同一平面的两个平面平行.(×)(可能相交,垂直于同一条直线的两个平面平行)②垂直于同一直线的两个平面平行.(√)(一条直线垂直于平行的一个平面,必垂直于另一个平面)③垂直于同一平面的两条直线平行.(√)5. ⑴ 垂线段和斜线段长定理:从平面外一点向这个平面所引的垂线段和斜线段中,①射影相等的两条斜线段相等,射影较长的斜线段较长;②相等的斜线段的射影相等,较长的斜线段射影较长;③垂线段比任何一条斜线段短.。
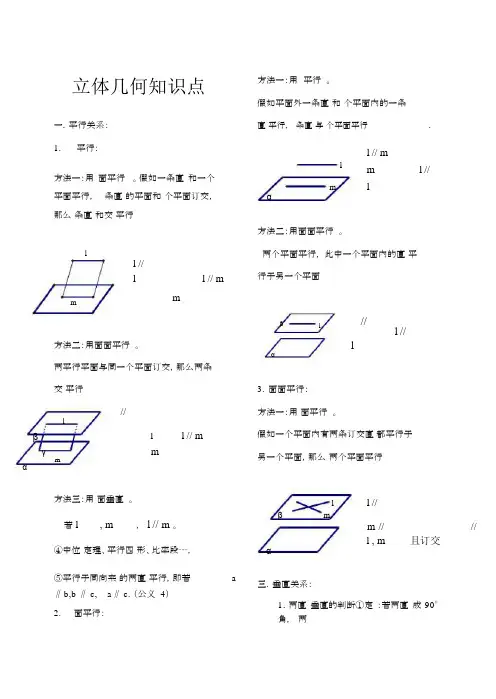
立体几何知识点一.平行关系:1.平行:方法一:用面平行。
假如一条直和一个平面平行,条直的平面和个平面订交,那么条直和交平行ll //l l // m 方法一:用平行。
假如平面外一条直和个平面内的一条直平行,条直与个平面平行.l // ml m l //m lα方法二:用面面平行。
两个平面平行,此中一个平面内的直平行于另一个平面mm方法二:用面面平行。
两平行平面与同一个平面订交,那么两条交平行//lβl l // mγmmα方法三:用面垂直。
若 l, m,l // m。
④中位定理、平行四形、比率段⋯⋯,⑤平行于同向来的两直平行,即若a∥b,b ∥ c, a∥ c. (公义 4)2.面平行:βl//l //lα3.面面平行:方法一:用面平行。
假如一个平面内有两条订交直都平行于另一个平面,那么两个平面平行l l //βm//m //l , m且订交α三.垂直关系:1.两直垂直的判断①定:若两直成 90°角,两直线相互垂直.方法一:用线面垂直实现。
一条直线垂直于一个平面,则垂直于这个平面内的随意一条直线 .l ll m mmα②一条直线与两条平行直线中的一条垂直,也必与另一条垂直 . 即若 b∥ c,a ⊥ b, 则 a⊥ c③假如一条直线与一个平面平行,那么这条直线与这个平面的垂线垂直 . 即若 a∥α ,b ⊥α , 则 a⊥ b.2.线面垂直:方法一:用线线垂直实现。
假如一条直线和一个平面内的两条订交直线都垂直,那么这条直线垂直于这个平面.lC l AC l ABAAC lαBAB AAC,AB方法二:用面面垂直实现。
假如两个平面相互垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面βlmlm l m,lα2.面面垂直:方法一:用线面垂直实现。
假如一个平面经过另一个平面的一条垂线,那么这两个平面相互垂直βl llα方法二:计算所成二面角为直角。
二.夹角问题。
( 一 )异面直线所成的角:(1)范围: (0 ,90 ](2)求法:方法一:定义法。
点线面的位置关系一(线面平行和面面平行)线面平行:1、判定定理:(1)平面外的一条直线与平面内的一条直线平行,则该直线与此平面平行(线线平行,则线面平行);方法:平行四边形法则+中位线法则(2)直线所在的一个平面与此平面平行,则该直线与此平面平行(面面平行,则线面平行);2、性质定理一条直线与一个平面平行,则过这条直线的任一平面和此平面的交线与该直线平行(线面平行,则线线平行);面面平行:1、判定定理:一个平面内的两条相交直线都与另一个平面平行,则这两个平面平行(线面平行,则面面平行);2、性质定理(1)两个平面平行,其中一个平面内的任何一条直线都与另一个平面平行;(2)两个平面平行,同时与第三个平面相交,则交线平行。
例题选讲:1、如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF,∠BCF=∠CEF=90°(1)求证:AE∥平面DCF;3、(全国卷)如图,直三棱柱111C B A ABC 中,E D ,分别是1,BB AB 的中点。
(1)证明:1BC //平面CD A 13.如图,在侧棱垂直底面的四棱柱ABCD -A 1B 1C 1D 1中,AD ∥BC ,E 是DD 1的中点,F 是平面B 1C 1E 与直线AA 1的交点.(1)证明:①EF ∥A 1D 1;线面垂直:3、判定定理:(3)一条直线与一个平面内的两条直交直线垂直,则这条直线垂直于这个面(线线垂直,则线面垂直);(4)两平面垂直,在其中一个平面内,垂直于交线的直线,则垂直于另一个平面(面面垂直,则线面垂直);方法:主动垂直+被动垂直4、性质定理(1)直线垂直于平面,则垂直于平面内的任意一条直线;(2)垂直于同一平面的两条直线平行;面面垂直:4、判定定理:如果一个平面过另一个平面的垂线,则这两个平面垂直(线面垂直,则面面垂直);5、性质定理若二平面垂直,那么在一个平面内垂直于它们的交线的直线垂直于另一个平面。
例题选讲:1、如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面P AD⊥平面ABCD,P A⊥AD.E 和F分别是CD和PC的中点.求证:(1)P A⊥底面ABCD;(2)BE∥平面P AD;(3)平面BEF⊥平面PCD.2、(全国卷)如图,三棱柱111C B A ABC -中,侧棱垂直底面ο90=∠ACB ,121AA BC AC ==,D 是侧棱1AA 的中点。
直线和平面垂直的定义:如果一条直线a 和一个平面 内的任意一条直线都垂直,我们就说直线a 和平面 互相垂直.直线a 叫做平面 的垂线,平面 叫做直线a 的垂面。
直线与平面垂直的判定定理(线线垂直→线面垂直):如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面。
基础例题:1、求证在正方体ABCD-A 1B 1C 1D 1中,体对角线AC 1垂直于面对角线BD2、AB 是圆O 的直径,C 是异于A 、B 的圆周上的任意一点,PA 垂直于圆O 所在的平面,证明:PAC BC 平面直线与平面垂直的性质定理(线面垂直→线线垂直):如果一条直线垂直于一个平面,那么他就和平面内的任意一条直线垂直。
基础例题1.已知:在空间四边形ABCD 中,AC =AD ,BC =BD ,中点为CD E ,求证:AB ⊥CD推论1(线线平行→线面垂直)如果在两条平行线中,有一条垂直于平面,那么另一条也垂直于这个平面。
CC1推论2(线面垂直→线线平行)如果两条直线同垂直于一个平面,那么这两条直线平行。
正方体AC 1中,EF 与异面直线AC,A 1D 都 垂直相交,交点分别为E,F , 求证:EF//BD 12、直线和平面平行的定义:如果一条直线和一个平面没有公共点,那么我们就说这条直线和这个平面平行。
直线和平面平行的判定定理(线线平行→线面平行):如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
基本例题:1已知:空间四边形ABCD 中,F E ,分别是AD AB ,的中点求证:BCD EF 平面//2、已知,空间四边形ABCD 中,H G F E ,,,分别是边DA CD BC AB ,,,的中点求证:EFG AC 平面//直线和平面平行的性质定理(线面平行→线线平行):如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
基础例题:如图,E 、H 分别是空间四边形ABCD 的边AB 、AD 的中点,平面α过EH 分别交BC 、CD 于F 、G.求证:EH ∥FG .四、两个平面的位置关系:(1)两个平面互相平行的定义:空间两平面没有公共点 (2)两个平面的位置关系:两个平面平行-----没有公共点; 两个平面相交-----有一条公共直线。
9.2 线面平行、面面平行一、明确复习目标1.掌握空间直线和平面、平面和平面的位置关系;2.掌握直线与平面、平面与平面平行的定义、判定和性质,并能运用这些知识进行论证或解题.3.能灵活进行“线线平行,线面平行,面面平行”之间的相互转化.二.建构知识网络1.直线和平面的位置关系有:(1)直线在平面内;(2)直线和平面相交;(3)直线和平面平行:定义——.2.线面平行的判定方法:①a∩α=ф⇒a∥α(定义法)②判定定理;③b⊥a, b⊥α, a⊄α⇒a∥α;④α∥β,a⊂α⇒a∥β⑤空间向量证线面平行.3线面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.4.判定平面平行的方法:(1)根据定义——证明两平面没有公共点;(2)判定定理——证明一个平面内的两条相交直线都平行于另一个平面;(3)证明两平面同垂直于一条直线.5.平行平面的主要性质:⑴由定义知:“两平行平面没有公共点”.⑵由定义推得:“两个平面平行,其中一个平面内的直线必平行于另一个平面。
⑶两个平面平行的性质定理:“如果两个平行平面同时和第三个平面相交,那么它们的交线平行”.⑷一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面.⑸夹在两个平行平面间的平行线段相等.⑹经过平面外一点只有一个平面和已知平面平行.三、双基题目练练手(2006重庆)对于任意的直线l与平面α,在平面α内必有直线m,使m与l()1.A.平行B.相交C.垂直D.互为异面直线2.一条直线同时平行于两个相交平面,那么这条直线与这两个平面的交线的位置关系是 ( ) A 异面 B 平行 C 相交 D 不能确定 3.(2005广东)给出下列关于互不相同的直线m 、l 、n 和平面α、β的四个命题: ①若,,m l A A m αα⊂⋂=∉点,则l 与m 不共面;②若m 、l 是异面直线,//,//,l m αα且,n l ⊥且,,n l n m n α⊥⊥⊥则;③若m l m l //,//,//,//则βαβα;④若,,l m αα⊂⊂l ∩m =点A ,l //β,//,//m βαβ则其中为假命题的是 ( )A .①B .②C .③D .④4.如果//αβ,AB 和CD 是夹在平面α、β之间的两条线段,AB ⊥CD ,且AB =2,直线AB 与平面α成300角,那么线段CD 的取值范围是 ( )A .⎪⎪⎭⎫ ⎝⎛334,332B .[)+∞,1C .⎥⎦⎤⎢⎣⎡332,1 D .⎪⎪⎭⎫⎢⎣⎡+∞,332 5.设D 是线段BC 上的点,BC ∥平面α,从平面α外一定点A (A 与BC 分居平面两侧)作AB 、AD 、AC 分别交平面α于E 、F 、G 三点,BC =a ,AD =b ,DF =c ,则EG =_____________.6.在四面体ABCD 中,M 、N 分别是面△ACD 、△BCD 的重心,则四面体的四个面中与MN 平行的是________.◆答案提示:1-4.CBCD ; 5.bac ab -; 6. 平面ABC 、平面ABD 四、经典例题做一做【例1】:如图,设a ,b 是异面直线,AB 是a ,b 的公垂线,过AB 的中点O 作平面α与a ,b 分别平行,M ,N 分别是a ,b 上的任意两点,MN 与α交于点P ,求证P 是MN 的中点.证明:连接AN ,交平面α与点Q ,连PQ ,∵b ∥α,b ⊂平面ABN ,平面ABN ∩α=OQ ,∴b ∥OQ ,又O 为AB 的中点,∴Q 为AN 的中点.∵a ∥α,a ⊂平面AMN 且平面AMN ∩α=PQ∴a ∥PQ . ∴P 为MN 的中点.【例2】如图,四面体A —BCD 被一平面所截,截面EFGH 是一个矩形.(1)求证:CD ∥平面EFGH .(2)求异面直线AB 、CD 所成的角.(3)若AB =a ,CD =b ,求截面EFGH 面积的最大值. (1)证明:∵截面EFGH 是一个矩形,∴EF ∥GH , 又GH ⊂平面BCD .∴EF ∥面BCD ,而EF ⊂面ACD ,面ACD ∩面BCD =CD .∴EF ∥CD ,∴CD ∥平面EFGH .(2)解:由(1)知CD ∥EF ,同理AB ∥FG ,由异面直线所成角的定义知∠EFG 即为所求的角.易得∠EFG =90︒. (3)答案:ab /4◆思悟提炼:灵活进行:“线线平行 线面平行”.【例3】 已知正四棱锥P —ABCD 的底面边长及侧棱长均为13,M 、N 分别是P A 、BD 上的点,且PM ∶MA =BN ∶ND =5∶8.(1)求证:直线MN ∥平面PBC ;(2)求直线MN 与平面ABCD 所成的角证明(1):∵P —ABCD 是正四棱锥,∴ABCD 是正方形.连结AN 并延长交BC 于点E ,连结PE .∵AD ∥BC ,∴EN ∶AN =BN ∶ND .又∵BN ∶ND =PM ∶MA ,_ C _B ABEH F GD∴EN ∶AN =PM ∶MA .∴MN ∥PE .又∵PE 在平面PBC 内,∴MN ∥平面PBC .解(2):由(1)知MN ∥PE ,∴求MN 与平面ABCD 所成的角即可.作PO ⊥面ABCD 于O ,连结OE ,则∠PEO 为PE 与平面ABCD 所成的角. 由正棱锥的性质知PO =22OB PB =2213. 由(1)知,BE ∶AD =BN ∶ND =5∶8,∴BE =865. 在△PEB 中,∠PBE =60°,PB =13,BE =865, 根据余弦定理,得PE =891. 在Rt △POE 中,PO =2213,PE =891, ∴sin ∠PEO =PEPO =724. 故MN 与平面ABCD 所成的角为arcsin 724. ◆思悟提炼:证线面平行,一般是转化为证线线平行.求直线与平面所成的角一般是作出线与面所成的角—转化为一个平面内的线线角.【例4】如下图,在正方体ABCD —A 1B 1C 1D 1中,AB =a .(1)求证:平面AD 1B 1∥平面C 1DB ;(2)求证:A 1C ⊥平面AD 1B 1;(3)求平面AB 1D 1与平面BC 1D 间的距离.(1)证明:∵D 1B 1∥DB ,∴D 1B 1∥平面C 1DB .同理,AB 1∥平面C 1DB .又D 1B 1∩AB 1=B 1,∴平面AD 1B 1∥平面C 1DB . A1(2)证明:∵A 1C 1⊥D 1B 1,而A 1C 1为A 1C 在平面A 1B 1C 1D 1上的射影,∴A 1C 1⊥D 1B 1. 同理,A 1C ⊥AB 1,D 1B 1∩AB 1=B 1.∴A 1C ⊥平面AD 1B 1.(3)解:设A 1C ∩平面AB 1D 1=M ,A 1C ∩平面BC 1D =N ,O 1、O 分别为上底面A 1B 1C 1D 1、下底面ABCD 的中心. 则M ∈AO 1,N ∈C 1O ,且AO 1∥C 1O ,MN 的长等于平面AD 1B 1与平面C 1DB 的距离,即MN =A 1M =NC =31A 1C =33a . 五.提炼总结以为师1.直线和平面平行的判定方法:2.证明两平面平行的常用方法:3.解题中,要注意灵活地实施下面的转化: 线线⇔线面⇔面面;立体几何⇔平面几何;从而使问题简同步练习 9.2线面平行、面面平行1.α、β是两个不重合平面,l ,m 是两条不重合直线,那么α∥β的一个充分条件是( )A .l ⊂α,m ⊂α,l ∥β,m ∥βB .l ⊂α,m ⊂β,l ∥mC .l ⊥α,m ⊥β,l ∥mD .l ∥α,m ∥β,l ∥m2.(2005年高考·湖北卷·文8)已知a 、b 、c 是直线,β是平面,给出下列命题: ①若c a c b b a //,,则⊥⊥;②若c a c b b a ⊥⊥则,,//;③若b a b a //,,//则ββ⊂;④若a 与b 异面,且ββ与则b a ,//相交;⑤若a 与b 异面,则至多有一条直线与a ,b 都垂直.其中真命题的个数是( )A .1B .2C .3D .43.设线段AB 、CD 是夹在两平行平面α、β之间的异面线段,点A 、C ∈α,B 、D ∈β,若M 、N 分别是AB 、CD 的中点,则有 ( )A .MN =21(AC +BD B .MN >21(AC +BD ) C .MN <21(AC +BD ) D .MN 与21(AC +BD )大小关系不确定.【填空题】4.(2004全国Ⅰ)已知a 、b 为不垂直的异面直线,α是一个平面,则a 、b 在α上的射影有可能是①两条平行直线;②两条互相垂直的直线;③同一条直线;④一条直线及其外一点.在上面结论中,正确结论的编号是__________.(写出所有正确结论的编号)5.(2005湖南).已知平面βα,和直线,给出条件:①α//m ;②α⊥m ;③α⊂m ;④βα⊥;⑤βα//.(i )当满足条件 时,有β//m ;(ii )当满足条件 时,有β⊥m .(填所选条件的序号)6.以下六个命题:(1)垂直于同一条直线的两个平面平行;(2)平行于同一条直线的两个平面平行;(3)平行于同一平面的两个平面平行;(4)与同一条直线成等角的两个平面平行;(5)一个平面上不共线三点到同一平面的距离相等,则这两个平面平行;(6)两个平面分别与第三个平面相交所得的两条交线平行,则这两个平面平行.其中正确命题的序号是____________.◆答案提示: 1-3.CAC ; 4.①②④5.③⑤,②⑤ ;6. 解:(1)、(3)【解答题】7.如下图,四棱锥P —ABCD 的底面是边长为a 的正方形,侧棱P A ⊥底面ABCD ,侧面PBC 内有BE ⊥PC 于E ,且BE =36 a ,试在AB 上找一点F ,使EF ∥平面P AD解:在面PCD 内作EG ⊥PD 于G ,连结AG ∵P A ⊥平面ABCD ,CD ⊥AD , ∴CD ⊥PD ∴CD ∥EG .又AB ∥CD ,∴EG ∥AB .若有EF ∥平面P AD ,则EF ∥AG ,∴四边形AFEG 为平行四边形,得EG =AF .∵CE =22)36(a a -=33a ,△PBC 为直角三角形, ∴BC 2=CE ·CP ⇒CP =3a ,AB AF =CD EG =PC PE =a a a 3333-=32 故得AF ∶FB =2∶1时,EF ∥平面P AD .8.如图,A ,B ,C ,D 四点都在平面α,β外,它们在α内的射影A 1,B 1,C 1,D 1是平行四边形的四个顶点,在β内的射影A 2,B 2,C 2,D 2在一条直线上,求证:ABCD 是平行四边形.证明:∵ A ,B ,C ,D 四点在β内的射影A 2,B 2,C 2,D 2在一条直线上,∴A ,B ,C ,D 四点共面.又A ,B ,C ,D 四点在α内的射影A 1,B 1,C 1,D 1是平行四边形的四个顶点, ∴平面ABB 1A 1∥平面CDD 1C 1.∴AB ,CD 是平面ABCD 与平面ABB 1A 1,平面CDD 1C 1的交线.∴AB ∥CD .同理AD ∥BC .∴四边形ABCD 是平行四边形.9.P 是ABC ∆所在平面外一点,'A 、'B 、'C 分别是 PBC ∆、PCA ∆、PAB ∆的重心,(1)求证:平面ABC C B A 平面||''';(2)求ABC C B A S S ∆∆:'''证明:分别连P A ,,PB ,,PC ,并延长分别交BC ,AC ,AB 于D ,E ,F则D ,E ,F 分别是BC ,CA ,AB 的中点.,,23PA PC PD PF∴== ∴A ,C ,||FD , 同理A ,B ,||DE ,∴平面ABC C B A 平面||''' AB C D B 1 D 1 C 1 α A 1 B 2 A 2 C 2 D 2 β(2)//AB DE Q∴32,,==PD PA DE AB , 又DE =21AB ∴31,,=AB B A , 易证∆A ,B ,C ,∽ABC ∆∴ABC C B A S S ∆∆:'''=1:9 10.如下图,设P 为长方形ABCD 所在平面外一点,M 、N 分别为AB 、PD 上的点,且MB AM =NPDN ,求证:直线MN ∥平面PBC 。
立体几何知识点总结一、平面通常用一个平行四边形来表示.平面常用希腊字母α、β、γ…或拉丁字母M、N、P来表示,也可用表示平行四边形的两个相对顶点字母表示,如平面AC.在立体几何中,大写字母A,B,C,…表示点,小写字母,a,b,c,…l,m,n,…表示直线,且把直线和平面看成点的集合,因而能借用集合论中的符号表示它们之间的关系,例如:a)A∈l—点A在直线l上;A∉α—点A不在平面α内;b)l⊂α—直线l在平面α内;c)a⊄α—直线a不在平面α内;d)l∩m=A—直线l与直线m相交于A点;e)α∩l=A—平面α与直线l交于A点;f)α∩β=l—平面α与平面β相交于直线l.二、平面的基本性质公理1 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.公理2 如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线.公理3 经过不在同一直线上的三个点,有且只有一个平面.根据上面的公理,可得以下推论.推论1 经过一条直线和这条直线外一点,有且只有一个平面.推论2 经过两条相交直线,有且只有一个平面.推论3 经过两条平行直线,有且只有一个平面.公理4 平行于同一条直线的两条直线互相平行三、证题方法四、空间线面的位置关系共面平行—没有公共点(1)直线与直线相交—有且只有一个公共点异面(既不平行,又不相交)直线在平面内—有无数个公共点(2)直线和平面直线不在平面内平行—没有公共点(直线在平面外) 相交—有且只有一公共点(3)平面与平面相交—有一条公共直线(无数个公共点)平行—没有公共点五、异面直线的判定证明两条直线是异面直线通常采用反证法.有时也可用定理“平面内一点与平面外一点的连线,与平面内不经过该点的直线是异面直线”.六、线面平行与垂直的判定(1)两直线平行的判定①定义:在同一个平面内,且没有公共点的两条直线平行.②如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行,即若a∥α,a ∥β④垂直于同一平面的两直线平行,即若a⊥α,b⊥α,则a∥b(线面垂直的性质定理)⑤两平行平面与同一个平面相交,那么两条交线平行,即若α∥β,α∩γ,β∩γ=b,则a∥b(面面平行的性质公理)⑥中位线定理、平行四边形、比例线段……,α∩β=b,则a∥b.(线面平行的判定定理)③平行于同一直线的两直线平行,即若a∥b,b∥c,则a∥c.(公理4)(2)两直线垂直的判定①定义:若两直线成90°角,则这两直线互相垂直.②一条直线与两条平行直线中的一条垂直,也必与另一条垂直.即若b∥c,a⊥b,则a⊥c③一条直线垂直于一个平面,则垂直于这个平面内的任意一条直线.即若a⊥α,b⊂α,a⊥b.④三垂线定理和逆定理:在平面内的一条直线,若和这个平面的一条斜线的射影垂直,则它也和这条斜线垂直.⑤如果一条直线与一个平面平行,那么这条直线与这个平面的垂线垂直.即若a∥α,b⊥α,则a⊥b.(3)直线与平面平行的判定①定义:若一条直线和平面没有公共点,则这直线与这个平面平行.②如果平面外一条直线和这个平面内的一条直线平行,则这条直线与这个平面平行.即若a⊄α,b⊂α,a ∥b,则a∥α.(线面平行的判定定理)③两个平面平行,其中一个平面内的直线平行于另一个平面,即若α∥β,l⊂α,则l∥β.(4)直线与平面垂直的判定①定义:若一条直线和一个平面内的任何一条直线垂直,则这条直线和这个平面垂直.②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面.即若m⊂α,n⊂α,m∩n=B,l⊥m,l⊥n,则l⊥α.(线面垂直判定定理)③如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于同一平面.即若l∥a,a⊥α,则l⊥α.④一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面,即若α∥β,l⊥β,则l⊥α.⑤如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面,即若α⊥β,a∩β=α,l⊂β,l⊥a,则l⊥α.(面面垂直的性质定理)(5)两平面平行的判定①定义:如果两个平面没有公共点,那么这两个平面平行,即无公共点⇔α∥β.②如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行,即若a,b⊂α,a∩b=P,a ∥β,b∥β,则α∥β.(面面平行判定定理)推论:一个平面内的两条直线分别平行于另一平面内的两条相交直线,则这两个平面平行,即若a,b⊂α,c,d⊂β,a∩b=P,a∥c,b∥d,则α∥β.(6)两平面垂直的判定①定义:两个平面相交,如果所成的二面角是直二面角,那么这两个平面互相垂直,即二面角α-a-β=90°⇔α⊥β.②如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直,即若l⊥β,l⊂α,则α⊥β.(面面垂直判定定理)七、空间中的各种角等角定理及其推论定理若一个角的两边和另一个角的两边分别平行,并且方向相同,则这两个角相等.推论若两条相交直线和另两条相交直线分别平行,则这两组直线所成的锐角(或直角)相等.1、异面直线所成的角(1)定义:a 、b 是两条异面直线,经过空间任意一点O ,分别引直线a ′∥a,b ′∥b,则a ′和b ′所成的锐角(或直角)叫做异面直线a 和b 所成的角.(2)取值范围:0°<θ≤90°. (3)求解方法①根据定义,通过平移,找到异面直线所成的角θ; ②解含有θ的三角形,求出角θ的大小. 2、直线和平面所成的角——斜线和射影所成的锐角 (1)取值范围0°≤θ≤90° (2)求解方法①作出斜线在平面上的射影,找到斜线与平面所成的角θ. ②解含θ的三角形,求出其大小. 3、二面角及二面角的平面角(1)半平面 直线把平面分成两个部分,每一部分都叫做半平面.(2)二面角 条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,这两个平面叫做二面角的面,即二面角由半平面一棱一半平面组成.若两个平面相交,则以两个平面的交线为棱形成四个二面角.二面角的大小用它的平面角来度量,通常认为二面角的平面角θ的取值范围是0°<θ≤180° (3)二面角的平面角①以二面角棱上任意一点为端点,分别在两个面内作垂直于棱的射线,这两条射线所组成的角叫做二面角的平面角.如图,∠PCD 是二面角α-AB-β的平面角.平面角∠PCD 的大小与顶点C 在棱AB 上的位置无关. ②二面角的平面角具有下列性质:(i)二面角的棱垂直于它的平面角所在的平面,即AB ⊥平面PCD.(ii)从二面角的平面角的一边上任意一点(异于角的顶点)作另一面的垂线,垂足必在平面角的另一边(或其反向延长线)上.(iii)二面角的平面角所在的平面与二面角的两个面都垂直,即平面PCD ⊥α,平面PCD ⊥β. ③找(或作)二面角的平面角的主要方法.(i)定义法 (ii)垂面法 (iii)三垂线法 (Ⅳ)根据特殊图形的性质 (4)求二面角大小的常见方法先找(或作)出二面角的平面角θ,再通过解三角形求得θ的值. 八.空间的各种距离 点到平面的距离(1)定义 面外一点引一个平面的垂线,这个点和垂足间的距离叫做这个点到这个平面的距离. (2)求点面距离常用的方法: 1)直接利用定义求①找到(或作出)表示距离的线段;②抓住线段(所求距离)所在三角形解之.2)体积法其步骤是:①在平面内选取适当三点,和已知点构成三棱锥;②求出此三棱锥的体积V 和所取三点构成三角形的面积S ;③由V=31S ·h ,求出h 即为所求.这种方法的优点是不必作出垂线即可求点面距离.难点在于如何构造合适的三棱锥以便于计算.直线和平面的距离、平行平面的距离将线面、面面距离转化为点面距离,然后运用解三角形或体积法求解之.空间直线和平面(一)知识结构(二)平行与垂直关系的论证1、线线、线面、面面平行关系的转化:线线∥线面∥面面∥公理4(a//b,b//c a//c)线面平行判定 αβαγβγ//,// ==⇒⎫⎬⎭a b a b面面平行判定1a b a b a //,//⊄⊂⇒⎫⎬⎭ααα面面平行性质a b a b A a b ⊂⊂=⇒⎫⎬⎪⎭⎪ααββαβ,//,//// 线面平行性质a ab a b////αβαβ⊂=⇒⎫⎬⎪⎭⎪ 面面平行性质1αβαβ////a a ⊂⇒⎫⎬⎭面面平行性质αγβγαβ//////⎫⎬⎭⇒A bα aβ abα2. 线线、线面、面面垂直关系的转化:线线⊥线面⊥面面⊥三垂线定理、逆定理PA AO POaa OA a POa PO a AO⊥⊂⊥⇒⊥⊥⇒⊥ααα,为在内射影则线面垂直判定1面面垂直判定a ba b Ol a l bl,,⊂=⊥⊥⇒⊥⎫⎬⎪⎭⎪ααaa⊥⊂⇒⊥⎫⎬⎭αβαβ线面垂直定义lal a⊥⊂⇒⊥⎫⎬⎭αα面面垂直性质,推论2αβαββα⊥=⊂⊥⇒⊥⎫⎬⎪⎭⎪ba a ba,αγβγαβγ⊥⊥=⇒⊥⎫⎬⎪⎭⎪aa面面垂直定义αβαβαβ=--⇒⊥⎫⎬⎭l l,且二面角成直二面角3. 平行与垂直关系的转化:线线∥线面⊥面面∥线面垂直判定2面面平行判定2线面垂直性质2面面平行性质3a bab//⊥⇒⊥⎫⎬⎭ααaba b⊥⊥⇒⎫⎬⎭αα//aa⊥⊥⇒⎫⎬⎭αβαβ//αβαβ//aa⊥⊥⎫⎬⎭a4. 应用以上“转化”的基本思路——“由求证想判定,由已知想性质。
”5. 唯一性结论:(三)空间中的角与距离 1. 三类角的定义:(1)异面直线所成的角θ:0°<θ≤90°(2)直线与平面所成的角:0°≤θ≤90° (时,∥或)θαα=︒⊂0b b(3)二面角:二面角的平面角θ,0°≤θ≤180°2. 三类角的求法:转化为平面角“一找、二作、三算”即:(1)找出或作出有关的角; (2)证明其符合定义; (3)指出所求作的角; (4)计算大小。
3. 空间距离:将空间距离转化为两点间距离——构造三角形,解三角形,求该线段的长。
4. 点到面的距离,线线间距离、线面间距离、面面间距离都可转化为点到面的距离。
常用方法:三垂线法、垂面法、体积法、向量法等。
知识点归纳必须熟练掌握基本概念、基本定理,熟练进行符号、文字、图形语言之间的转化。
1、平面的基本性质----3个公理、3个推论线线平行线面平行面面平行3、掌握①⇔⇔线线垂直线面垂直面面垂直②⇔⇔。