(浙教版)九年级数学下册《第二章直线与圆的位置关系》期末专题试卷(含答案解析)

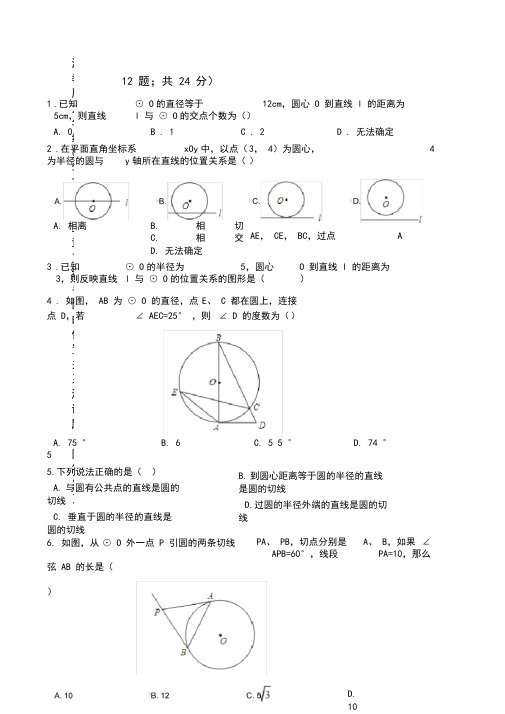
12 题；共 24 分） 1 .已知 ⊙ O 的直径等于 12cm ，圆心 O 到直线 l 的距离为 5cm ，则直线 l 与 ⊙ O 的交点个数为（）A. 0 B . 1 C . 2 D . 无法确定2 .在平面直角坐标系 xOy 中，以点（ 3， 4）为圆心，4为半径的圆与 y 轴所在直线的位置关系是（ ）A. 相离B. 相切C. 相交D. 无法确定3 .已知 ⊙ O 的半径为 5，圆心 O 到直线 l 的距离为3，则反映直线 l 与 ⊙ O 的位置关系的图形是（ ） 4 . 如图， AB 为 ⊙ O 的直径，点 E 、 C 都在圆上，连接 点 D ，若 ∠ AEC=25° ，则 ∠ D 的度数为（ ）A. 75 °B. 6 55.下列说法正确的是（ ） A. 与圆有公共点的直线是圆的切线 C. 垂直于圆的半径的直线是圆的切线 C. 5 5 ° D. 74 ° B. 到圆心距离等于圆的半径的直线是圆的切线 D.过圆的半径外端的直线是圆的切线PA 、 PB ，切点分别是 A 、 B ，如果 ∠APB=60°，线段PA=10，那么浙教版九年级数学下册第二章直线与圆的位置关系测试题（附答案） 弦 AB 的长是（ ） D. 106. 如图，从 ⊙ O 外一点 P 引圆的两条切线AE ， CE ， BC ，过点A7.如 L是⊙ O 的切线，要判定AB⊥ L，还需要添加的条件是（）A. AB 经过圆心OB. AB是直径C. AB是直径， B 是切点D. AB是直线，B是切点8.已知Rt△ACB，∠ACB=90°，I 为内心，CI交 AB 于 D，BD= ， AD= ，则S△ACB=（）D . 7.59 .在平面直角坐标系中，以点（ 2， 3）为圆心，2 为半径的圆必定（ ）A. 与 x 轴相离，与 y 轴相切B. 与 x 轴， y 轴都相离C. 与 x 轴相切，与y 轴相离 D. 与 x 轴， y 轴都相切10 .如图， ⊙ O 1 的半径为１， 正方形ABCD 的边长为 6， 点 O 2为正方形ABCD 的中心， O 1O 2垂直AB 于 P 点，O 1O 2 =8． 若将 ⊙ O 1 绕点 P 按顺时针方向旋转 360°， 在旋转过程中， ⊙ O 1 与正方形 ABCD 的边只有一个公共 点的情况一共出现：11 .如图， ⊙ O 内切于正方形 ABCD ，边 AD ， CD 分别与 ⊙ O 切于点 E ， F ，点 M 、 N 分别在线段 DE ，DF 上，且 MN 与 ⊙ O 相切，若 △ MBN 的面积为8，则 ⊙ O 的半径为（ ）A. B. 2 C. D. 2二、填空题（共 8 题；共 24 分）13 .如图， 是 的直径， 是 上的点，过点 作 的切线交 的延长线于点 .若∠ A=32 ，则°______ 度．A. 12A. 3 次B. 5次C. 6次D. 7 次12.如图， 过半径为 6 的圆 O 上一点 A 作圆 O 的切线 l ， P 为圆 O 的一个动点， 作 PH ⊥ l 于点 H ， 连接 PA ．如14.如图，一个宽为 2 cm 的刻度尺在圆形光盘上移动，当刻度尺的一边与光盘相切时，另一边与光盘边缘两个交点处的读数恰好是“ 2和” “ 10（单位：”______ c m），那么该光盘的直径是cm.15.⊙ O 的半径为3cm， B为⊙ O外一点，OB交⊙ O 于点 A，AB=OA，动点P从点 A出发，以π cm/s 的速度在⊙ O 上按逆时针方向运动一周回到点A立即停止．当点____ P运动的时间为s 时， BP与⊙ O相切．16.若直角三角形两边分别为 6 和 8，则它内切圆的半径为．17.如图，△ ABC中，AB=AC=5cm， BC=8cm，以 A为圆心，3cm?长为半径的圆与直线B C的位置关系是．18.如图, 是⊙ 的直径，分别与⊙ 相切于点，若，则图中阴影部分的面积为______ .19.如图，在△ ABC中，∠ ABC和∠ACB的平分线相交于点G，过点G作EF∥BC交 AB 于E，交AC于F，过点 G 作 GD⊥ AC于 D，下列四个结论: ① EF=BE+CF；② ∠ BGC=9°0+∠ A；③ 点 G到△ABC各边的距离相等；④ 设 GD= AE+AF= 则，其中正确结论有（填序号）.B 两点，与y 轴交于C 点，⊙ B 的圆心为 B，半长．径是 1，点 P是直线AC上的动点，过点P 作⊙ B的切线，切点是Q，则切线长PQ的最小值是21.已知：如图，⊙ O内切于△ ABC，∠ BOC=105°，∠ ACB=90°， AB=20cm．求BC、 AC的22.如图，AB为⊙ O的直径，点C在⊙ O外，∠ ABC的平分线与⊙ O交于点D，∠ C=90° ．1） CD与⊙ O有怎样的位置关系？请说明理由；2）若∠ CDB=6°0， AB=6，求的长．23.如图，在 △ ABC 中， A B ＝AC ，以AB 为直径作 ⊙ O 交 BC 于点 D.过点 D 作 EF ⊥ AC ，垂足为E ，且交AB的延长线于点 F.1）求证： EF 是 ⊙ O 的切线； 2）若 AB ＝ 8， ∠ A ＝ 60°，求 B D 的长 .D 为 ⊙ O 上一点，点C 在直径 BA 的延长线上，且 ∠ CDA ＝ ∠CBD ．1）求证： CD 是 ⊙ O 的切线；2）过点 B 作 ⊙ O 的切线交 CD 的延长线于点 E ， BC ＝ 6， 25.如图，在平面直角坐标系中，半径为 1 的 ⊙ A 的圆心与坐标原点 O 重合，线段 BC 的端点分别在 x 轴与y 轴上，点B 的坐标为（ 6， 0），且 sin ∠ OCB= ．（ 1）若点 Q 是线段 BC 上一点，且点 Q 的横坐标为 m ．① 求点 Q 的纵坐标；（用含 m 的代数式表示） ② 若点 P 是 ⊙ A 上一动点，求 PQ 的最小值； （ 2）若点 A 从原点 O 出发，以1 个单位/秒的速度沿折线 OBC 运动，到点 C 运动停止， ⊙ A 随着点 A 的运 动而移动．24.如图，．求 BE 的长．①点 A 从 O→B 的运动的过程中，若⊙ A 与直线 BC相切，求 t 的值；②在⊙ A整个运动过程中，当⊙ A与线段BC有两个公共点时，直接写出t 满足的条件．23 . （ 1）证明：连接 O D ，AD ， ∵ AB 是 ⊙ O 的直径， ∴ AD ⊥ BC ， AB ＝ AC ， ∴ BD ＝ CD ， OA ＝ OB ， ∴ OD ∥ AC ，EF ⊥ AC ， ∴ OD ⊥ EF ， ∴ EF 是 ⊙ O 的切线； 2）解： ∵ AB ＝ A C ， A D ⊥ BC ， ∴ ∠ BAD ＝ ∠ BAC＝ 30°， BD ＝ AB ＝＝ 4.答案1. C2.C3.B4.B5. B6. A7.C8.B9.A 10. B 11. B 12.C 13.26 14.10 15.1 或 5 16. 2 或 -1 17.相切 18. 19. ①③④ 20.21.解： ∵ 圆 O 内切于 △ ABC ， ∴ ∠ ABO=∠ CBO ， ∠ BCO=∠ ACO ， ∵ ∠ ACB=90，° ∴ ∠ BCO= × 90=4° 5 ，° ∵ ∠ BOC=105，° ∴ ∠ CBO=180 ° -45 ° -105， ∴° ∠ =3A0BC ° =2∠ CBO=60，° ∴ ∠ A=30 ，° ∴ BC= AB= × 20=10cm ， ∴ AC= BC 、 AC 的长分别是10cm 、 cm. 22. （ 1）解：相切．理由如下：连接 OD ， ∵ BD 是 ∠ ABC 的平分线， ∴ ∠ CBD=∠ ABD ， 又 ∵ OD=OB ， ∴ ∠ ODB=∠ ABD ， ∴ ∠ ODB=∠ CBD ， ∴ OD ∥ CB ， （ 2）解：若 ∠ CDB=6°0，可得 ∴ ∠ ODC=∠ C=90，° ∴ CD 与 ⊙ O 相 ODB=3°0 ， 切；∠ AOD=60 ，° 又 ∵ AB=6， ∴ AO=3， = =π ．24.（ 1）解：连接 OD.OB＝ OD，∴ ∠ OBD＝∠ BDO.∠CDA＝∠CBD，∴ ∠ CDA＝∠ ODB.∵ AB 是⊙ O 的直径，∴ ∠ ADB＝ 90°，∴ ∠ ADO＋∠ ODB ＝ 90°，∠ADO＋∠CDA＝90 °，即∠CDO＝ 90 °，∴ OD⊥CD.OD 是⊙ O的半径，∴ CD是⊙ O的切线；2）解：∵ ∠C＝∠C，∠CDA＝∠CBD，∴ △ CDA∽△CBD，BC＝ 6，∴ CD＝ 4.CE， BE是⊙ O的切线，BE＝ DE， BE⊥ BC，BE2＋ BC2＝ EC2，BE2＋ 62＝（4＋ BE）2，BE＝.25.（ 1）解：① ∵ 点 B的坐标为（6， 0），tan∠ OCB= ，BC=10， OC=8，BC的解析式为y=kx+b，，点 Q 的横坐标为m ，点 Q 的纵坐标为﹣m+8；如图1，作OQ⊥ AB 交⊙ A于 P，则此时PQ 最小，× AB× OQ= × BO× C， OOQ=4.8，PQ 最小=OQ 最小﹣ 1=3.8；2）解：① 如图2，⊙ A与直线BC相切于H，AH⊥ BC，又∠ BOC=9°0，△ BHA∽ △ BOC，，即解得， BA= ，则OA=6﹣= ，∴ t= 时，⊙ A 与直线 BC相切；②由（ 2）①得， t= 时，⊙ A与直线 BC相切，当 t=5 时，⊙ A经过点B，当 t=7 时，⊙ A经过点B，当t=15 时，⊙ A经过点C，故 < t≤5 或 7≤ t≤ 1时，5 ⊙ A与线段 BC有两个公共点．。

浙教版九年级下册数学第二章直线与圆的位置关系含答案一、单选题(共15题，共计45分)1、如图AB、BC、CD分别与⊙O 相切于E、 F、G 三点且AB DC，则下列结论：①CG=CF；②BE=BF；③∠BOC=90°；④△BEO～△BOC～△OGC中正确的个数是（）A.4B.3C.2D.12、如图，⊙O为△ABC的内切圆，AC=10，AB=8，BC=9，点D，E分别为BC，AC 上的点，且DE为⊙O的切线，则△CDE的周长为（）A.9B.7C.11D.83、如图，小明同学测量一个光盘的直径，他只有一把直尺和一块三角板，他将直尺、光盘和三角板如图放置于桌面上，并量出AB＝3cm，则此光盘的半径是（）A.3 cmB.3 cmC.6 cmD.6 cm4、如图，在平面直角坐标系中，过格点A，B，C作一圆弧，点B与下列格点的连线中，能够与该圆弧相切的是（）A.点（0，3）B.点（2，3）C.点（5，1）D.点（6，1）5、如图，△ABC中，下面说法正确的个数是（）个．①若O是△ABC的外心，∠A=50°，则∠BOC=100°；②若O是△ABC的内心，∠A=50°，则∠BOC=115°；③若BC=6，AB+AC=10，则△ABC的面积的最大值是12；④△ABC的面积是12，周长是16，则其内切圆的半径是1．A.1B.2C.3D.46、如图，在O中，AB是直径，AC是弦，过点C的切线与AB的延长线交于点D，若∠A=25°，则∠D的大小为（）A.25°．B.40°．C.50°．D.65°．7、下列命题中正确的是（）A.平分弦的直径垂直于弦B.与直径垂直的直线是圆的切线C.对角线互相垂直的四边形是菱形D.联结等腰梯形四边中点的四边形是菱形8、如图，PA，PB分别与相切于A，B两点，PO与AB相交于点C，，，则OC的长等于A. B.3 C. D.9、直线l上有一点到圆心O的距离等于⊙O的半径，则直线l与⊙O的位置关系是( )A.相离B.相切C.相切或相交D.相交10、如图，AB是⊙O的直径，直线PA与⊙O相切于点A，PO交⊙O于点C，连接BC，若∠BCO=a，则∠P的度数为( )A.2aB.90°-2aC.45°-2aD.45°+2a11、下列说法错误的是（）A.有一个角是直角的菱形是正方形B.相等的圆周角所对的弧不一定相等 C.垂直于半径的直线是圆的切线 D.有一个锐角对应相等的两个直角三角形相似12、如图，⊙O内切于△ABC，切点为D、E、F，∠B=45°，∠C=55°，连接OE、OF、OE、OF，则∠EDF等于（）A.45°B.55°C.50°D.70°13、如图，AB为⊙O的直径，C、D是⊙O上的两点，∠CDB＝25°，过点C作⊙O的切线交AB的延长线于点E，则∠E的度数为（）A.40°B.50°C.55°D.60°14、如图，AB是⊙O的弦，AC是⊙O的切线，A为切点，BC经过圆心．若∠B=25°，则∠C的大小等于（）A.20°B.25°C.40°D.50°15、以坐标原点O为圆心，作半径为2的圆，若直线y=－x+b与⊙O相交，则b 的取值范围是（）A. .B.C.D.二、填空题(共10题，共计30分)16、如图，在△ABC中，AB=CB，以AB为直径的⊙O交AC于点D，过点C作CF ∥AB，在CF上取一点E，使DE=CD，连接AE，对于下列结论：①AD=DC；②△CBA∽△CDE；③= ；④AE为⊙O的切线，一定正确的结论选项是________．17、如图，点A、B、D在⊙O上，∠A=25°，OD的延长线交直线BC于点C，且∠OCB=40°，直线BC与⊙O的位置关系为________．18、如图，已知半圆O的直径AB为12，OP=1，C为半圆上一点，连结CP。

浙教版九年级下册数学第二章直线与圆的位置关系含答案一、单选题(共15题，共计45分)1、如图，在中，，，，以为直径作圆与斜边交于点，则的长为（）A. B. C. D.2、下列命题错误的是（）A.经过三个点一定可以作圆B.同圆或等圆中，相等的圆心角所对的弧相等C.三角形的外心到三角形各顶点的距离相等D.经过切点且垂直于切线的直线必经过圆心3、如图，已知⊙O的弦AB=8，以AB为一边作正方形ABCD，CD边与⊙O相切，切点为E，则⊙O半径为（）A.10B.8C.6D.54、如图,O是正方形ABCD的对角线BD上一点,☉O与边AB,BC都相切,点E,F分别在边AD,DC上.现将△DEF沿着EF折叠,折痕EF与☉O相切,此时点D恰好落在圆心O处.若DE=2,则正方形ABCD的边长是( )A.3B.4C.2+D.25、如图，点P在⊙O外，PA、PB分别与⊙O相切于A、B两点，∠P=50°，则∠AOB等于（）A.150°B.130°C.155°D.135°6、如图，AB是⊙O的直径，直线PA与⊙O相切于点A，PO交⊙O于点C，连接BC，若∠BCO=a，则∠P的度数为( )A.2aB.90°-2aC.45°-2aD.45°+2a7、如图，已知PA是⊙O的切线，A为切点，PC与⊙O相交于B．C两点，PB＝2㎝，BC＝8㎝，则PA的长等于( )A.4㎝B.16㎝C.20㎝D.2 ㎝8、四边形中，一定有内切圆的是（）A.平行四边形B.菱形C.矩形D.以上答案都不对9、如图AB、BC、CD分别与⊙O 相切于E、 F、G 三点且AB DC，则下列结论：①CG=CF；②BE=BF；③∠BOC=90°；④△BEO～△BOC～△OGC中正确的个数是（）A.4B.3C.2D.110、如图，AD、AE、CB均为⊙O的切线，D、E、F分别为切点，AD=8，则△ABC 的周长为（）A.8B.10C.12D.1611、如图，在等边△ABC中，BC=2，⊙A与BC相切于点D，且与AB，AC分别交于点E，F，则的长是（）A. B. C. D. π12、如图，过⊙O外一点P引⊙O的两条切线PA，PB，切点分别是A，B，OP交⊙O于点C，点D是上不与点A、点C重合的一个动点，连接AD，CD，若∠APB=80°，则∠ADC的度数是（）A.15°B.20°C.25°D.30°13、如图，点A，B，C在⊙O上，∠ABC=29°，过点C作⊙O的切线交OA的延长线于点D，则∠D的大小为（）A.29°B.32°C.42°D.58°14、如图，在平面直角坐标系中，A（0，2 ），动点B，C从原点O同时出发，分别以每秒1个单位和每秒2个单位长度的速度沿x轴正方向运动，以点A为圆心，OB的长为半径画圆；以BC为一边，在x轴上方作等边△BCD.设运动的时间为t秒，当⊙A与△BCD的边BD所在直线相切时，t的值为（）A. B. C.4 ＋6 D.4 －615、下列命题是真命题的个数有（）①垂直于半径的直线是圆的切线②平分弦的直径垂直于弦③若是方程x﹣ay=3的一个解，则a=﹣1④若反比例函数的图象上有两点，则y1＜y2．A.1个B.2个C.3个D.4个二、填空题(共10题，共计30分)16、如图是一个古代车轮的碎片，小明为求其外圆半径，连结外圆上的两点A、B，并使AB与车轮内圆相切于点D，做CD⊥AB交外圆于点C．测得CD=10cm，AB=60cm，则这个车轮的外圆半径为________ cm．17、如图，在△ABC中，∠C=90°，CA=4，CB=3. 与CA延长线、AB、CB延长线相切，切点分别为E、D、F，则该弧所在圆的半径为________．18、在中，，，，则的内切圆的半径为________.19、已知⊙O的半径为3cm，圆心O到直线l的距离是4cm，则直线l与⊙O的位置关系是________ ．20、如图，两个圆都以为圆心，大圆的弦与小圆相切于点，若，则圆环的面积为________.21、如图，在四边形中，．若，则的内切圆面积________（结果保留）．22、如图，PA、PB分别切⊙O于A、B，并与⊙O的另一条切线分别相交于D、C 两点，已知PA=6，则△PCD的周长=________23、已知的半径为，圆心到直线/的距离是，则直线/与的位置关系________24、如图，AB为⊙O的直径，且AB＝4，点C在半圆上，OC⊥AB，垂足为点O，P为半圆上任意一点，过P点作PE⊥OC于点E，设△OPE的内心为M，连接OM、PM.当点P在半圆上从点B运动到点A时，内心M所经过的路径长为________.25、如图，PA、PB是⊙O的两条切线，A，B是切点，若∠APB=60°，PO=2，则PB=________．三、解答题(共5题，共计25分)26、如图1，一个圆球放置在V型架中．图2是它的平面示意图，CA、CB都是⊙O的切线，切点分别是A、B，如果⊙O的半径为cm，且AB=6cm，求∠ACB．27、如图，从⊙O外一点P引⊙O的两条切线PA、PB，切点分别是A、B，若PA=5cm，C是上的一个动点（点C与A、B两点不重合），过点C作⊙O的切线，分别交PA、PB于点D、E，求△PED的周长是多少？28、已知：如图，在中，，以为直径的交于点，过点作于点．求证：是的切线．29、如图，△ABC中，∠C=90°，点G是线段AC上的一动点（点G不与A、C 重合），以AG为直径的⊙O交AB于点D，直线EF垂直平分BD，垂足为F，EF 交BC于点E，连结DE．（1）求证：DE是⊙O的切线；（2）若cosA=， AB=8， AG=2，求BE的长；（3）若cosA=， AB=8，直接写出线段BE的取值范围．30、如图，PA、PB切⊙O于A、B，若∠APB=60°，⊙O半径为3，求阴影部分面积．参考答案一、单选题(共15题，共计45分)1、A2、A3、D4、C6、B7、D8、B9、A10、D11、C12、C13、B14、C15、B二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、三、解答题(共5题，共计25分)26、27、28、30、。

浙教版九年级下册数学第二章直线与圆的位置关系含答案一、单选题(共15题，共计45分)1、如图，AB是⊙O直径，点C在⊙O上，AE是⊙O的切线，A为切点，连接BC 并延长交AE于点D ．若∠AOC=80°，则∠ADB的度数为（）A.40°B.50°C.60°D.20°2、1.下列说法中，不正确的是( )A.三角形的内心是三角形三条内角平分线的交点B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部C.垂直于半径的直线是圆的切线D.三角形的内心到三角形的三边的距离相等3、如图，直线y＝x＋与x轴、y轴分别相交于A、B两点，圆心P的坐标为（1，0），⊙P与y轴相切于点O．若将⊙P沿x轴向左移动，当⊙P与该直线相交时，满足横坐标为整数的点P的个数是（）A.3B.4C.5D.64、如图，直角三角形ABC的内切圆分别与AB，BC相切于D点、E点，根据图中标示的长度与角度，求AD的长度为何？（）A. B. C. D.5、如图，AB是⊙O的切线，B为切点，AO与⊙O交于点C，若∠BAO=40o，则∠OCB的度数为( )A.40°B.50°C.65°D.75 °6、如图，直线AB、CD相交于点O，∠AOD=30°，半径为1cm的⊙P的圆心在射线OA上，且与点O的距离为6cm．如果⊙P以1cm/s的速度沿由A向B的方向移动，那么（）秒钟后⊙P与直线CD相切．A.4B.8C.4或6D.4或87、如图所示，∠APB＝30°，O为PA上一点，且PO＝6，以点O为圆心，半径为3 的圆与PB的位置关系是（）A.相离B.相切C.相交D.相切、相离或相交8、如L是⊙O的切线，要判定AB⊥L，还需要添加的条件是（）A.AB经过圆心OB.AB是直径C.AB是直径，B是切点D.AB是直线，B是切点9、如图，在中，是的内切圆，连结，，则图中阴影部分的面积之和为（）A. B. C.12 D.1410、已知⊙O的半径是3 cm，若圆心O到直线l的距离为1 cm，则⊙O与直线l的位置关系是（）A.相交B.相切C.相离D.无法确定11、如图，为的切线，切点为A，连接，与交于点C，延长与交于点D，连接，若，则的度数为( )A. B. C. D.12、如图，在△ABC中，AB=10，AC=8，BC=6，以边AB的中点O为圆心，作半圆与AC相切，点P，Q分别是边BC和半圆上的动点，连接PQ，则PQ长的最大值与最小值的和是（）A.6B.2 +1C.9D.13、如图，圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上．已知铁片的圆心为O，三角尺的直角顶点C落在直尺的10cm处，铁片与直尺的唯一公共点A落在直尺的14cm处，铁片与三角尺的唯一公共点为B，下列说法错误的是（）A.圆形铁片的半径是4cmB.四边形AOBC为正方形C.弧AB的长度为4πcmD.扇形OAB的面积是4πcm 214、如图，以Rt△ABC的直角边AB为直径作半圆⊙O与边BC交于点D，过D作半圆的切线与边AC交于点E，过E作EF∥AB，与BC交于点F．若AB＝20，OF ＝7.5，则CD的长为（）A.7B.8C.9D.1015、如图，∠ACB＝60°，半径为2的⊙O切BC于点C，若将⊙O在CB上向右滚动，则当滚动到⊙O与CA也相切时，圆心O移动的水平距离为（）A.2πB.4πC.2D.4二、填空题(共10题，共计30分)16、若一三角形的三边长分别为5、12、13，则此三角形的内切圆半径为________．17、如图，圆弧形弯道两边的直道在连接点处与弯道相切，测得，圆弧的半径是2千米，则该段圆弧形歪道的长为________千米.（结果保留）18、如图，半径为的⊙与边长为的等边三角形的两边、都相切，连接，则________.19、在Rt△ABC中，∠C=90°，AC=3，BC=4．若以C点为圆心，r为半径所作的圆与斜边AB只有一个公共点，则r的取值范围是________．20、如图，在矩形 ABCD 中，AB=2，BC=4，⊙D 的半径为 1．现将一个直角三角板的直角顶点与矩形的对称中心O重合，绕着O点转动三角板，使它的一条直角边与⊙D切于点H，此时两直角边与AD交于E，F两点，则EH的值为________.21、如图，Rt△ABC中，∠C=90°，∠ABC=30°，AB=6．点D在AB边上，点E 是BC边上一点（不与点B、C重合），且DA=DE，则AD的取值范围是________．22、在△ABC中，已知∠ACB＝90°，BC＝3，AC＝4，以点C为圆心，2.5为半径作圆，那么直线AB与这个圆的位置关系分别是________.23、如图，⊙O与AC相切于点A，BC过圆心O，圆周角∠B＝25°，则∠C的度数为________．24、如图，直线y=- x-3交x轴于点A，交y轴于点B，点P是x轴上一动点，以点P为圆心，以1个单位长度为半径作⊙P，当⊙P与直线AB相切时，点P的坐标是________.25、已知，如图，CB是⊙O的切线，切点为B，连接OC，半径OA⊥OC，连接AB 交OC于点D，若OD=1，OA=3，则BC=________．三、解答题(共5题，共计25分)26、已知：如图，四边形ABCD是⊙O的内接矩形，AB＝4，BC＝3，点E是劣弧上的一点，连接AE，DE．过点C作⊙O的切线交线段AE的延长线于点F，若∠CDE＝30°，求CF的长．27、如图，已知点E在直角△ABC的斜边AB上，以AE为直径的⊙O与直角边BC相切于点D，求证：AD平分∠BAC.28、如图，AB是⊙O的直径，点F、C是⊙O上两点，且==，连接AC，AF，过点C作CD⊥AF交AF延长线于点D，垂足为D．（1）求证：CD是⊙O的切线；（2）若CD=2，求⊙O的半径．29、如图，AB是⊙O的直径，CD与⊙O相切于点C，DA⊥AB，DO及DO的延长线与⊙O分别相交于点E、F，EB与CF相交于点G．（1）求证：DA=DC；（2）⊙O的半径为3，DC=4，求CG的长．30、已知AB是⊙O的直径，CD是⊙O的弦，AB与CD交于E，CE=DE，过B作BF ∥CD，交AC的延长线于点F，求证：BF是⊙O的切线．参考答案一、单选题(共15题，共计45分)1、B2、C3、A4、D5、C6、D7、C8、C9、B10、A11、D12、C13、C14、C15、C二、填空题(共10题，共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题，共计25分)26、28、30、。

期末复习：浙教版九年级数学下册第二章直线与圆的位置关系一、单选题（共10题；共30分）1.到三角形三边距离都相等的点是三角形（）的交点A. 三边中垂线B. 三条中线C. 三条高D. 三条内角平分线2.如图，△ABC中，AB=5，BC=3，AC=4，以点C为圆心的圆与AB相切，则⊙C的半径为（）A. 2.3B. 2.4C. 2.5D. 2.63.如图所示，从⊙O 外一点A 引圆的切线AB，切点为B，连接AO并延长交圆于点C，连接BC，已知∠A＝26°，则∠ACB 的度数为（）A. 32°B. 30°C. 26°D. 13°4.如图，点O是∠BAC的边AC上的一点，⊙O与边AB相切于点D，与线段AO相交于点E，若点P是⊙O 上一点，且∠EPD=35°，则∠BAC的度数为（）A. 20°B. 35°C. 55°D. 70°5.如图，AB是⊙O的切线，B为切点，AO与⊙O交于点C，若∠BAO=30°，则∠OCB的度数为（）A. 30°B. 60°C. 50°D. 40°6.圆外切等腰梯形的中位线等于8，则一腰长等于（）A. 4B. 6C. 8D. 107.如图，直线AB、CD、BC分别与⊙O相切于E、F、G，且AB∥CD，若OB=6cm，OC=8cm，则BE+CG的长等于（）A. 13B. 12C. 11D. 108.如图，AB是⊙O的直径，⊙O交BC的中点于D，DE⊥AC于E，连接AD，则下列结论：①AD⊥BC；②∠EDA=∠B；③OA= AC；④DE是⊙O的切线，正确的个数是（）A. 1 个B. 2个C. 3 个D. 4个9.已知⊙O的半径是6cm，点O到同一平面内直线l的距离为5cm，则直线l与⊙O的位置关系是（）A. 相交B. 相切C. 相离D. 无法判断10.如图，AB是⊙的直径，CD是∠ACB的平分线交⊙O于点D，过D作⊙O的切线交CB的延长线于点E．若AB=4，∠E=75°，则CD的长为（）A. B. 2 C. 2 D. 3二、填空题（共10题；共30分）11.如图，四边形ABCD是平行四边形，其中边AD是⊙O的直径，BC与⊙O相切于点B，若⊙O的周长是12π，则四边形ABCD的面积为________．12.如图，已知：⊙O与△ABC的边AB，AC，BC分别相切于点D，E，F，若AB＝4，AC＝5，AD＝1，则BC ＝________．13.在平面直角坐标系中，以点（2，1）为圆心，半径为1的圆与x轴的位置关系是________．（填“相切”、“相离”或“相交”）14.如图，两个同心圆，大圆半径为5cm，小圆的半径为3cm，若大圆的弦AB与小圆相交，则弦AB的取值范围是________ ．15.直角三角形两直角边为3，4，则其外接圆和内切圆半径之和为________．16.在直角三角形中，若两条直角边长分别为6cm和8cm，则三角形的内切圆半径与外接圆半径之比为________.17.如图，在⊙O中，AC是弦，AD是切线，CB⊥AD于B，CB与⊙O相交于点E，连接AE，若AE平分∠BAC，BE=1，则CE=________．18.已知：如图，AB=BC，∠ABC=90°，以AB为直径的⊙O交OC与点D，AD的延长线交BC于点E，过D 作⊙O的切线交BC于点F．下列结论：①CD2=CE·CB；②4EF 2=ED ·EA；③∠OCB=∠EAB；④ ．其中正确的只有________．（填序号）19.如图：半径为2的圆心P在直线y=2x﹣1上运动，当⊙P与x轴相切时圆心P的坐标为________．20.如图，边长为2的正方形ABCD内接于⊙O，过点D作⊙O的切线交BA延长线于点E，连接EO，交AD 于点F，则EF长为________．三、解答题（共8题；共60分）21.如图，P为⊙O外一点，PO交⊙O于C，过⊙O上一点A作弦AB⊥PO于E，若∠EAC=∠CAP，求证：PA 是⊙O的切线．22.已知：如图，AB是⊙O的直径，BC是和⊙O相切于点B的切线，⊙O的弦AD平行于OC．求证：DC是⊙O的切线.23.在Rt△ABC中，∠ACB=90°，BE平分∠ABC，D是边AB上一点，以BD为直径的⊙O经过点E，且交BC 于点F．（1）求证：AC是⊙O的切线；（2）若BF=6，⊙O的半径为5，求CE的长．24.如图，AB是⊙O的直径，点F、C在⊙O上且，连接AC、AF，过点C作CD⊥AF交AF的延长线于点D．（1）求证：CD是⊙O的切线；（2）若，CD=4，求⊙O的半径．25.如图,已知△ABC内接于⊙O,点D在OC的延长线上,∠B＝∠CAD＝30°.（1）AD是⊙O的切线吗？为什么？（2）若OD⊥AB,BC=5,求⊙O的半径.26.如图，AE是圆O的直径，点B在AE的延长线上，点D在圆O上，且AC⊥DC，AD平分∠EAC(1)求证：BC是圆O的切线。

浙教版九年级下册数学第二章直线与圆的位置关系含答案一、单选题(共15题，共计45分)1、下列结论中，正确的是 ( )A.圆的切线垂直于经过切点的半径B.垂直于切线的直线必经过切点 C.垂直于切线的直线必经过圆心 D.垂直于半径的直线是圆的切线2、如图，点P为圆O外一点，PA为圆的切线，PO交圆O于点B，∠P=30°，OB=4,则线段BP的长为（）A.6B.C.4D.83、如图，AB是⊙O的直径，⊙O交BC的中点于D，DE⊥AC于E，连接AD，则下列结论：①AD⊥BC；②∠EDA=∠B；③OA= AC；④DE是⊙O的切线，正确的个数是（）A.1 个B.2个C.3 个D.4个4、如图，与切于点，，是上一点，连接并延长与交于点，连接，，，则的长为（）A. B. C. D.5、如图，在△ABC中，∠A＝60°，AB＝4，以BC的中点O为圆心作圆，分别与AB、AC相切于D、E两点，则的长是（）A. πB.πC. πD.36、如图，已知AB是⊙O的直径，⊙O的切线CD与AB的延长线交于点D，点C 为切点，联接AC，若∠A＝26°，则∠D的度数是（）A.26°B.38°C.42°D.64°7、如图，是四边形的内切圆，下列结论一定正确的有（）个：① ；② ；③ ；④ ．A.1B.2C.3D.48、如图，等腰的内切圆⊙ 与，，分别相切于点，，，且，，则的长是( )A. B. C. D.9、如图，PA，PB分别与相切于A，B两点，PO与AB相交于点C，，，则OC的长等于A. B.3 C. D.10、如图，在等腰三角形△ABC中，O为底边BC的中点，以O为圆心作半圆与AB，AC相切，切点分别为D，E．过半圆上一点F作半圆的切线，分别交AB，AC于M，N．那么的值等于（）A. B. C. D.111、若的半径，点O到直线的距离为3，下列图中位置关系正确的是（）A. B. C.D.12、如图，在半径为5的中，将劣弧沿弦翻折，使折叠后的恰好与、相切，则劣弧AB的长为（）A. B. C. D.13、已知直线l与半径为2的⊙O的位置关系是相离，则点O到直线l的距离的取值范围在数轴上的表示正确的是（）A. B. C. D.14、在平面直角坐标系xOy中，经过点（sin45°，cos30°）的直线，与以原点为圆心，2为半径的圆的位置关系是（）A.相交B.相切C.相离D.以上三者都有可能15、如图，在矩形ABCD中，AB=3，BC=4，O为矩形ABCD的中心，以D为圆心1为半径作⊙D，P为⊙D上的一个动点，连接AP、OP，则△AOP面积的最大值为（）A.4B.C.D.二、填空题(共10题，共计30分)16、⊙O的半径r=5cm，点P在直线l上，若OP=5cm，则直线l与⊙O的位置关系是________。

浙教版九年级下册数学第二章直线与圆的位置关系含答案一、单选题(共15题，共计45分)1、如图，AB与⊙O相切于点A，BO与⊙O相交于点C，点D是优弧AC上一点，∠CDA=27°，则∠B的大小是（）A.27°B.34°C.36°D.54°2、如图，在平面直角坐标系中，点P在第一象限，⊙P与x轴相切于点Q，与y轴交于M（0，2），N（0，8）两点，则点P的坐标是（）A.（5，3）B.（3，5）C.（5，4）D.（4，5）3、如图，PA、PB是⊙O的切线，切点分别为A、B，C为⊙O上一点，若∠P=50°，则∠ACB=（）A.40°B.50°C.65°D.130°4、如图，PA，PB是⊙O的切线，切点分别为A，B，点C在⊙O上，且是优弧，则∠ACB等于（）A.180°﹣2∠PB.180°﹣∠PC.90°﹣∠PD.∠P5、如图，已知是的两条切线，A，B为切点，线段交于点M．给出下列四种说法：①；②；③四边形有外接圆；④M是外接圆的圆心，其中正确说法的个数是（）A.1B.2C.3D.46、以坐标原点O为圆心，作半径为2的圆，若直线y=﹣x+b与⊙O相交，则b 的取值范围是（）A.0≤b＜2B.﹣2C.﹣2 2D.﹣2 ＜b＜27、如图，在菱形ABCD中，AB＝2 ，∠C＝120°，以点C为圆心的与AB，AD分别相切于点G，H，与BC，CD分别相交于点E，F，若用扇形CEF作一个圆锥的侧面，则这个圆锥的高是（）A.2B.3C.2D.28、如图，圆O是Rt△ABC的外接圆，∠ACB=90°，∠A=25°，过点C作圆O的切线，交AB的延长线于点D，则∠D的度数是（）A.25°B.40°C.50°D.65°9、如图，矩形ABCD中，AB=4，BC=3，连接AC，⊙P和⊙Q分别是△ABC和△ADC的内切圆，则PQ的长是（）A. B. C. D.210、如图，与相切于点，若，则的度数为（）A. B. C. D.11、如图，过⊙O上一点C作⊙O的切线，交⊙O直径AB的延长线于点D.若∠D ＝40°，则∠A的度数为（）A.20°B.25°C.30°D.40°12、如图，AB是⊙O的切线，A为切点，连接OA，OB，若∠B＝20°，则∠AOB 的度数为（）A.40°B.50°C.60°D.70°13、如图，在ABCD中，∠DAB＝60°，AB＝8，AD＝6.⊙O分别切边AB，AD于点E，F，且圆心O好落在DE上.现将⊙O沿AB方向滚动到与BC边相切（点O 在ABCD的内部），则圆心O移动的路径长为（）A.2B.4C.5﹣D.8﹣214、将正方形ABCD绕点A按逆时针方向旋转30°，得正方形AB1C1D1， B1C1交CD于点E，AB=，则四边形AB1ED的内切圆半径为（）A. B. C. D.15、如图，圆O是Rt△ABC的外接圆，∠ACB=90°，∠A=25°，过点C作圆O 的切线，交AB的延长线于点D，则∠D的度数是（）A.25°B.40°C.50°D.65°二、填空题(共10题，共计30分)16、如图，AB是⊙O的直径，AD是⊙O的切线，点C在⊙O上，BC∥OD，AB=2，OD=3，则BC的长为________.17、如图，△ABC是一块绿化带，将阴影部分修建为花圃，已知AB=13，AC=5，BC=12，阴影部分是△ABC的内切圆，这个圆的半径为________．18、如图，直线分别交x轴、y轴于A、B两点，已知点C坐标为（6,0），若直线AB上存在点P，使∠OPC=90°，则m的取值范围是________。

浙教版九年级数学下册期末专题复习：第二章直线与圆的位置关系一、单选题（共10题；共30分）1.若直线l与☉O有公共点,则直线l与☉O的位置关系可能是( )A. 相交或相切B. 相交或相离C. 相切或相离D. 无法确定2.如图，直线AB是⊙O的切线，C为切点，OD∥AB交⊙O于点D，点E在⊙O上，连接OC，EC，ED，则∠CED的度数为（）A. 30°B. 35°C. 40°D. 45°3.到三角形三边距离都相等的点是三角形（）的交点A. 三边中垂线B. 三条中线C. 三条高D. 三条内角平分线4.如图，直线l是⊙O的切线，点A为切点，B为直线l上一点，连接OB交⊙O于点C，D是优弧AC上一点，连接AD，CD.若∠ABO=40°.则∠D的大小是（）A. 50°B. 40°C. 35°D. 25°5.直线l与半径r的圆O相交，且点O到直线l的距离为6，则r的取值范围是( )A. r<6B. r=6C. r>6D. r≥66.给出下列四个结论，其中正确的结论为（）A. 菱形的四个顶点在同一个圆上；B. 三角形的外心到三个顶点的距离相等；C. 正多边形都是中心对称图形；D. 若圆心到直线上一点的距离恰好等于圆的半径，则该直线是圆的切线.7.已知三角形三边长分别为5cm、5cm、6cm，则这个三角形内切圆的半径是（）A. cmB. cmC. 2cmD. 3cm8.如图，AB为半圆O的直径，AD、BC分别切⊙O于A，B两点，CD切⊙O于点E，AD与CD相交于D，BC与CD相交于C，连结OD、OE、OC，对于下列结论：①AD+BC=CD；②∠DOC=90°；③S梯形ABCD=CD•OA；④．其中结论正确的个数是（）A. 1B. 2C. 3D. 49.如图，⊙O中，PC切⊙O于点C，连PO交于⊙O点A、B，点F是⊙O上一点，连PF，CD ⊥AB于点D，AD=2，CD=4，则PF：DF的值是（）A. 2B.C. 5：3D. 4：310.如图，⊙O的半径为2，点O到直线l的距离为3，点P是直线l上的一个动点．若PB切⊙O 于点B，则PB的最小值是（）A. B. C. 3 D. 2二、填空题（共10题；共30分）11.如图，是的直径，是上的点，过点作的切线交的延长线于点.若∠A=32°，则∠________度．12.如图，四边形ABCD内接于⊙O，AB是直径，过C点的切线与AB的延长线交于P点，若∠P=40°，则∠D的度数为________．13.如图，已知：⊙O与△ABC的边AB，AC，BC分别相切于点D，E，F，若AB＝4，AC＝5，AD＝1，则BC＝________．14.如图，直线与半径为2的⊙O相切于点是⊙O上点，且∠，弦，则的长度为________15.如图所示，⊙M与轴相交于点A（2，0），B（8，0），与y轴相切于点C，则圆心M的坐标是________ ．16.如图，在△ABC中，∠A=45°，AB= ，AC=6，点D，E为边AC上的点，AD=1，CE=2，点F为线段DE上一点（不与D，E重合），分别以点D、E为圆心，DF、EF为半径作圆.若两圆与边AB，BC共有三个交点时，线段DF长度的取值范围是________.17.如图，半径为3的⊙O与Rt△AOB的斜边AB切于点D，交OB于点C，连接CD交直线OA 于点E，若∠B=30°，则线段AE的长为________．18.已知圆O的半径为5，AB是圆O的直径，D是AB延长线上一点，DC是圆O的切线，C是切点，连接AC，若∠CAB=30°，则BD的长为________．19.如图，在矩形ABCD中，AB=4，AD=2，点E在CD上，DE=1，点F是边AB上一动点，以EF为斜边作Rt△EFP．若点P在矩形ABCD的边上，且这样的直角三角形恰好有两个，则AF 的值是________。