— P3-1 —第五章 离散系统的时域分析习题解答5-1. 画出下列各序列的图形：。
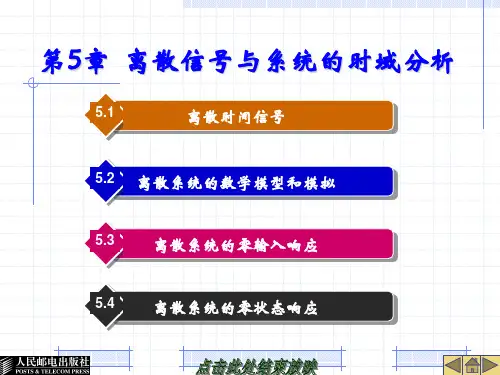
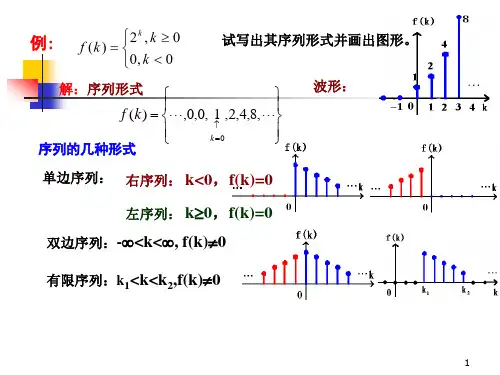
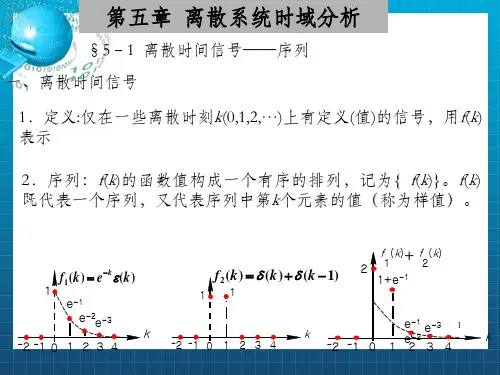
)2()( )6( );()()( )5( );()()( )4(; 0 ,)2(30,2)( )3( );1()12()( )2( );2()( )1(16315324321k f k f k f k f k f k f k f k f k k k k f k k f k k k f kk-==+=⎩⎨⎧<+=++=+=-/εε5-2 写出图示各序列的表达式。
解： )6()3(2)()( )d ( )1()1()( )c ()]6()3([2)( )b ( )]5()1()[1()( )a (41321---+-=--=---=----=-k kk k f k k f k k k f k k k k f k εεεεεεεε5-3. 判断以下序列(A 、B 为正数)是否为周期序列，若是周期序列，试求其周期。
)(sin )( )3( )()2( )873cos()( )1(08)(k k A k f e k f k B k f kj εωπππ==-=-解：; 14 , , 14)732( )1(=∴=T 且它为周期序列为有理数ππ (a)(b)— 2 —. , )( )3(;, 16)812( )2(它为非周期序列为单边函数它为非周期序列为无理数∴∴=k f ππ5-4.解：)]1()1()([1)(1100---+=k y b k f a k f a b k y 即：)1()()1()(1010-+=-+k f a k f a k y b k y b ，为一阶的。
5-5. 列写图示系统的差分方程，指出其阶次。
解：)1()()2()1()(1021-+=----k f a k f a k y b k y b k y ，二阶的。
5-6. 如果在第k 个月初向银行存款x (k )元，月息为α，每月利息不取出，试用差分方程写出第k 个月初的本利和y (k )，设x (k )510元，α50.0018，y (0)520元，求y (k )，若k 512，则y (12)为多少。
