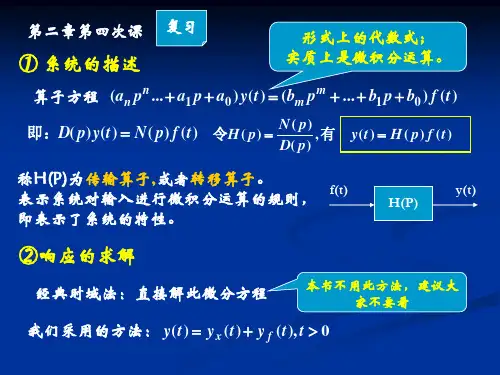
信号与系统分析《信号与系统分析》吴京,国防科技大学出版社第二章-4
- 格式:ppt
- 大小:213.00 KB
- 文档页数:9




信号与系统实验讲义吴彬安徽师范大学物理与电子信息学院二○一○年一月前言“信号与系统”是无线电技术、自动控制、通信工程、生物医学电子工程、信号图象处理、空间技术等专业的一门重要的专业基础课,也是国内各院校相应专业的主干课程。
当前,科学技术的发展趋势既高度综合又高度分化,这要求高等院校培养的大学生,既要有坚实的理论基础,又要有严格的工程技术训练,不断提高实验研究能力、分析计算能力、总结归纳能力和解决各种实际问题的能力。
21世纪要求培养“创造型、开发型、应用型”人才,即要求培养智力高、能力强、素质好的人才。
由于该课程核心的基本概念、基本理论和分析方法都非常重要,而且系统性、理论性很强,为此在学习本课程时,开设必要的实验,对学生加深理解深入掌握基本理论和分析方法,培养学生分析问题和解决问题的能力,以及使抽象的概念和理论形象化、具体化,对增强学习的兴趣有极大的好处,做好本课程的实验,是学好本课程的重要教学辅助环节。
在做完每个实验后,请务必写出详细的实验报告,包括实验方法、实验过程与结果、心得和体会等。
目录实验一基本运算单元 (3)实验二用同时分析法观测50H z非正弦周期信号的分解与合成 (9)实验三无源和有源滤波器 (13)实验四二阶网络函数的模拟 (18)实验五二阶网络状态轨迹的显示 (22)实验六抽样定理 (27)实验七MATLAB在信号与系统的时域分析中的应用 (31)实验八MATLAB在信号与系统的变换域分析中的应用 (40)附录一TKSS-C型信号与系统实验箱 (51)附录二扫频电源操作使用说明 (55)实验一 基本运算单元一、实验目的1、熟悉由运算放大器为核心元件组成的基本运算单元;2、掌握基本运算单元特性的测试方法。
二、实验设备与仪器1、信号与系统实验箱TKSS-C 型;2、双踪示波器。
三、实验原理1、运算放大器运算放大器实际就是高增益直流放大器,当它与反馈网络连接后,就可实现对输入信号的求和、积分、微分、比例放大等多种数学运算,运算放大器因此而得名。



信号与系统分析(吴冰著)课后答案下载吴冰的《信号与系统分析》主要内容包括信号与系统的基本概念,信号与系统的时域分析,连续时间信号与系统的频域分析,连续时间系统的复频域分析,离散信号与系统的变换域分析。
以下是要与大家分享的信号与系统分析(吴冰著),供大家参考!点击此处下载???信号与系统分析(吴冰著)课后答案???丛书名 21世纪高等院校信息与通信工程规划教材——精品系列标准书号 ISBN978-7-115-26076-5编目分类 TN911.6作者解培中周波编著出版社人民邮电出版社蒋亮开本 16开印张 12.75字数 312千字页数 198页装帧平装版次第1版第1次初版时间 xx年9月本印次 xx年9月首印数 --册定价 27.00元本书系统介绍了信号与系统的基本概念、基本理论和基本分析方法,可作为普通高等院校信号与系统相关课程的教材使用,也可供工程技术人员参考。
第1章信号与系统的基本概念 11.1 信号的描述与分类 11.1.1 信号的定义与描述 11.1.2 信号的分类 21.2 系统的描述与分类 61.2.1 系统的概念 61.2.2 系统的数学模型 61.2.3 系统的分类 71.3 信号与系统分析概述 121.3.1 信号与系统分析的基本内容与方法 121.3.2 信号与系统理论的应用 13练习题 14第2章信号与系统的时域分析 172.1 典型连续时间信号 172.1.1 复指数信号 172.1.2 单位阶跃信号 182.1.3 单位冲激信号 192.1.4 冲激偶信号 232.1.5 斜坡信号 242.2 典型离散时间信号 242.2.1 复指数序列 252.2.2 单位脉冲序列 272.2.3 单位阶跃序列 282.3 连续时间信号的基本运算 29 2.3.1 替换自变量的运算 292.3.2 信号的导数与积分 312.3.3 信号的相加与相乘 322.4 离散时间信号的基本运算 33 2.4.1 替换自变量的运算 332.4.2 相加与相乘 342.4.3 差分与累加 352.5 信号的时域分解 362.5.1 交、直流分解 362.5.2 奇、偶分解 362.5.3 实部、虚部分解 372.5.4 脉冲分解 372.6 连续系统的冲激响应 392.6.1 冲激响应的定义 392.6.2 冲激响应的物理解释 39 2.6.3 冲激响应的求取 402.7 离散系统的单位脉冲响应 442.8 连续系统的零状态响应 462.8.1 卷积分析法的引出 472.8.2 确定卷积积分限的公式 472.8.3 卷积的图解 482.8.4 卷积积分的性质 512.9 离散系统的零状态响应 562.9.1 离散卷积的引出 562.9.2 离散卷积的性质 572.9.3 确定离散卷积求和限的公式 582.9.4 离散卷积的图解 592.9.5 离散卷积的列表计算 602.10 系统的全响应 60练习题 63第3章连续时间信号与系统的频域分析 74 3.1 周期信号分解为傅里叶级数 743.1.1 三角形式傅里叶级数 743.1.2 指数形式傅里叶级数 773.2 周期信号的频谱 793.2.1 周期信号的频谱 793.2.2 周期信号的频谱特点 823.2.3 周期信号的频带宽度 823.2.4 周期信号的功率谱 843.3 非周期信号的频谱密度函数——傅里叶变换 85 3.3.1 非周期信号的频谱密度函数 853.3.2 傅里叶变换 863.3.3 常用信号的傅里叶变换 873.4 傅里叶变换的性质及其应用 913.4.1 傅里叶变换的性质和应用 913.4.2 频谱资源的有限性与认知无线电 1003.5 希尔伯特变换及小波变换简介 1013.5.1 希尔伯特变换 1013.5.2 小波变换简介 1033.6 取样信号的频谱 1043.6.1 时域取样 1043.6.2 时域取样定理 1073.6.3 压缩感知简介 1083.7 连续时间系统的频域分析 1083.7.1 虚指数信号的响应 1083.7.2 正弦信号的响应 1093.7.3 直流信号的响应 1093.7.4 非正弦周期信号 1093.7.5 非周期信号的响应 1103.7.6 频域系统函数 1103.8 信号的无失真传输和理想滤波器 1123.8.1 信号的无失真传输 1123.8.2 理想滤波器 113练习题 114第4章连续时间系统的复频域分析 1204.1 拉普拉氏变换 1204.1.1 拉普拉氏变换的定义 1204.1.2 拉氏变换的收敛域 1214.1.3 常用信号的拉氏变换 1224.2 拉氏变换的性质 1234.3 拉氏反变换 1304.4 连续系统的复频域分析 1334.4.1 求解系统微分方程 1334.4.2 分析电路 1344.5 系统函数 1384.5.1 系统函数 1384.5.2 系统函数的零、极点图 1394.5.3 系统函数的零、极点分布与系统冲激响应的关系 140 4.5.4 系统的稳定性 1424.6 连续系统的模拟 1434.6.1 基本运算器 1434.6.2 连续系统的模拟 144练习题 149第5章离散信号与系统的变换域分析 153 5.1 Z变换 1535.1.1 从拉氏变换到Z变换 1535.1.2 Z变换的定义 1545.1.3 Z变换的收敛域 1555.1.4 常见信号的Z变换 1565.2 Z变换的性质 1575.3 Z反变换 1665.3.1 幂级数展开法 1665.3.2 部分分式展开法 1675.4 离散系统的Z变换分析 1695.5 离散系统函数与系统特性 1745.6 离散系统的模拟 1765.6.1 基本运算器 1765.6.2 离散系统的模拟 176练习题 178附录1 常用信号的傅里叶变换 182附录2 傅里叶变换的基本性质 183附录3 常用信号的拉氏变换 184附录4 拉氏变换的基本性质 185附录5 常用序列的Z变换 186附录6 Z变换的性质 188附录7 信号与系统常用数学公式 189部分练习题参考答案 1901.信号与系统考试题及答案2.信号与系统答案-阳光大学生网3.信号与系统第三版段哲民课后答案西北工业大学出版社4.电力系统分析第二版(孟祥萍著)课后答案下载。


信号与系统分析信号与系统分析是一门重要的电子工程学科,它研究信号在系统中的传输、处理和表示,同时也研究系统对信号的响应和性能。
这门学科对于设计和实现各种电子设备和系统非常重要,在数字信号处理、通信系统和控制系统等领域得到广泛应用。
在这篇文章中,我将介绍信号与系统分析的基本概念、原理和应用。
信号是指在时间或空间上随时间变化的某种物理量,它可以用数学函数来表示。
例如,声音、图像、电压和电流等都是信号。
信号分为连续时间信号和离散时间信号两种类型。
连续时间信号是在时间上连续变化的信号,它的表示方式是连续的函数,例如正弦波。
离散时间信号是取样和量化得到的离散的信号,它的表示方式是序列,例如数字音频信号。
信号的分类还有频域和时域信号,频域信号是将信号在频率域中表示,时域信号是将信号在时间上表示。
系统是指对信号进行处理或传输的设备,这些设备可以是线性的或非线性的。
系统的输入是信号,系统的输出也是信号。
系统可以是电子电路、通信信道或传感器等各种设备。
系统可以用数学模型来描述,常见的模型有线性时不变(LTI)系统模型、状态空间模型和传递函数模型等。
LTI系统是指响应只依赖于输入的当前值和过去的值,它具有许多重要的性质,例如稳定性、因果性和线性性等。
通过对信号和系统的分析和处理,可以得到一些重要的性能指标。
例如,频率响应、相位响应、系统的零点和极点等。
这些指标可以衡量系统的性能和稳定性。
另外,还可以使用滤波器、模数转换器和数字信号处理器等工具来处理信号和系统。
信号与系统分析的应用非常广泛,包括数字信号处理、通信系统、控制系统、图像处理、声音处理和生物医学工程等领域。
在数字信号处理领域,信号与系统分析可以用于数字滤波器和变换器的设计和实现。
在通信系统中,信号与系统分析可以用于调制、解调和信道等设备的设计和实现。
在控制系统中,信号与系统分析可以用于控制器和反馈系统的设计和分析。
在图像处理和声音处理中,信号与系统分析可以用于图像增强和声音清晰化等处理。