下载文档原格式
机械振动测验一、填空题1、 所谓振动，广义地讲，指一个物理量在它的①平均值附近不停地经过②极大值和③极小值而往复变化。
2、 一般来说，任何具有④弹性和⑤惯性的力学系统均可能产生机械振动。
3、 XXXX 在机械振动中，把外界对振动系统的激励或作用，①激励或输入；而系统对外界影响的反应，称为振动系统的⑦响应或输出。
4、 常见的振动问题可以分成下面几种基本课题：1、振动设计2、系统识别3、环境预测5、 按激励情况分类，振动分为：①自由振动和②强迫振动；按响应情况分类，振动分为：③简谐振动、④周期振动和⑤瞬态振动。
6、 ①惯性元件、②弹性元件和③阻尼元件是离散振动系统三个最基本的元件。
7、 在系统振动过程中惯性元件储存和释放①动能，弹性元件储存和释放②势能，阻尼元件③耗散振动能量。
8、 如果振动时系统的物理量随时间的变化为简谐函数，称此振动为①简谐振动。
9、 常用的度量振动幅值的参数有：1、峰值2、平均值3、均方值4、均方根值。
10、 系统的固有频率只与系统的①质量和②刚度有关，与系统受到的激励无关。
二、 试证明：对数衰减率也可以用下式表示，式中n x 是经过n 个循环后的振幅。
1ln nx xn δ=三、 求图示振动系统的固有频率和振型。
已知12m m m ==，123k k k k ===。
北京理工大学1996年研究生入学考试理论力学（含振动理论基础）试题自己去查双（二）自由度振动J，在平面上在弹簧k的限制下作纯滚动，如图所示，四、圆筒质量m。
质量惯性矩o求其固有频率。
五、物块M质量为m1。
滑轮A与滚子B的半径相等，可看作质量均为m2、半径均为r的匀质圆盘。
斜面和弹簧的轴线均与水平面夹角为β，弹簧的刚度系数为k。
又m1 g>m2 g sinβ , 滚子B作纯滚动。
试用能量法求：（1）系统的微分方程；（2）系统的振动周期。
六、在下图所示系统中，已知m和k。
计算系统的基频。
机械振动基础试卷一、填空题（本题15分，每空1分）1、机械振动大致可分成为：（）和非线性振动；确定性振动和（）；（）和强迫振动。
2、在离散系统中，弹性元件储存( )，惯性元件储存（），（）元件耗散能量。
3、周期运动的最简单形式是（），它是时间的单一（）或（）函数。
4、叠加原理是分析（ ）系统的基础。
5、系统固有频率主要与系统的（）和（）有关，与系统受到的激励无关。
6、系统的脉冲响应函数和（）函数是一对傅里叶变换对，和（）函数是一对拉普拉斯变换对。
7、机械振动是指机械或结构在平衡位置附近的（ ）运动。
二、简答题（本题40分，每小题10分）1、 简述振动系统的实际阻尼、临界阻尼、阻尼比的联系与区别。
（10分）2、 共振具体指的是振动系统在什么状态下振动？简述其能量集聚过程？ （10分）3、 简述刚度矩阵[K]中元素k ij 的意义。
（10分）4、 简述随机振动问题的求解方法，以及与周期振动问题求解的区别。
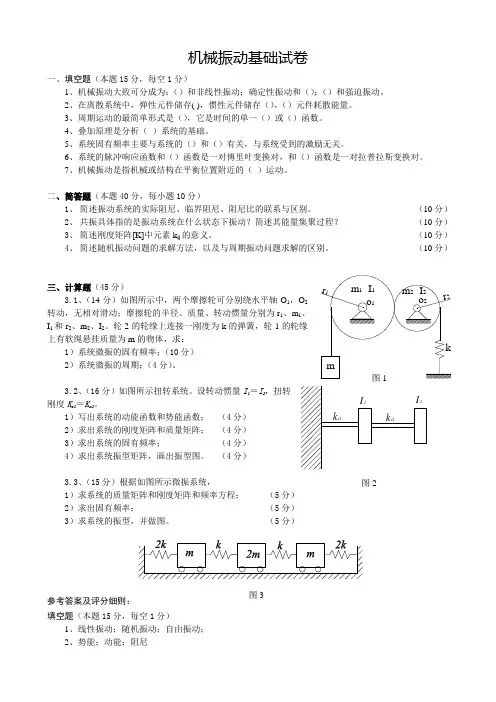
（10分）三、计算题（45分） 3.1、（14分）如图所示中，两个摩擦轮可分别绕水平轴O 1，转动，无相对滑动；摩擦轮的半径、质量、转动惯量分别为r 1、m I 1和r 2、m 2、I 2。
轮2的轮缘上连接一刚度为k 的弹簧，轮1上有软绳悬挂质量为m 的物体，求： 1）系统微振的固有频率；（10分）2）系统微振的周期；（4分）。
3.2、（16分）如图所示扭转系统。
设转动惯量I 1＝I 2，扭转刚度K r1＝K r2。
1）写出系统的动能函数和势能函数； （4分） 2）求出系统的刚度矩阵和质量矩阵； （4分）3）求出系统的固有频率； （4分）4）求出系统振型矩阵，画出振型图。
（4分）3.3、（15分）根据如图所示微振系统， 1）求系统的质量矩阵和刚度矩阵和频率方程； （5分）2）求出固有频率； （5分）3）求系统的振型，并做图。
（5分）参考答案及评分细则：填空题（本题15分，每空1分）1、线性振动；随机振动；自由振动；2、势能；动能；阻尼图2图33、简谐运动；正弦；余弦4、线性5、刚度；质量6、频响函数；传递函数7、往复弹性简答题（本题40分，每小题10分）5、 简述振动系统的实际阻尼、临界阻尼、阻尼比的联系与区别。
大学物理-机械振动习题-含答案一、选择题1. 质点作简谐振动，距平衡位置 2。
0cm 时， ，则该质点从一端运动到 C )C:2.2s --- 加速度 a=4.0cm /s 另一端的时间为( A:1.2s B: 2.4sD:4.4sX ,22.2s.2上 2 42 •—个弹簧振子振幅为2 10 2m 当t 0时振子在x 1.0 10 2m 处，且向 正方向运动，则振子的振动方 程是：[A ]A : 1.2题图22 10 cos( t )m ；3’6)m； 3)m；2 10 2 cos( t2 10 2 cos( tD :2x 2 10 cos( t —)m；解：由旋转矢量可 以得出振动的出现初相为：？3 •用余弦函数描述一简谐振动，若其速度与时间 -1v (m.s )1.3题图t (s )—►o 1 —v 2 m vm如图示，则振动的初相位为: (v —t )关系曲线[A ]A: e ； B : 3 ； C ： 2 ；D : 2- ;E :「3丁6解：振动速度为：V V max Si n( t 0)t 0时,sin 01，所以。
-或。
2 6由知1.3图，t 0时，速度的大小是在增加，由旋转矢量图知，旋转矢量在 第一象限内，对应质点的运动是由正最大 位移向平衡位置运动，速度是逐渐增加的， 旋转矢量在第二象限内，对应质点的运动 是由平衡位置向负最大位移运动，速度是 逐渐减小的，所以只有。
-是符合条件的。
64 •某人欲测钟摆摆长，将钟摆摆锤上移 1毫 米，测得此钟每分快0。
1秒，则此钟摆的 ) B:30cm C:45cm丄理丁 160mm 30cm2 dT 2 ( 0.1)：、填空题1 •有一放置在水平 面上的弹簧振子。
振幅A = 2.0 X 0_2m 周期摆长为( A:15cm D:60cm 解：单摆周期 有： 他2 . g,两侧分别对「和l 求导，j*T = 0.50s ,根据所给初始条件,作出简谐振动的矢量图,并写出振动方程式或初位相。
一、选择题1．两个质点各自作简谐振动，它们的振幅相同、周期相同，第一个质点的振动方程为1cos()x A t ωα=+。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处，则第二个质点的振动方程为 [ ]（A ）)π21cos(2++=αωt A x ； （B ）)π21cos(2-+=αωt A x ；（C ）)π23cos(2-+=αωt A x ； （D ）)cos(2π++=αωt A x 。
答案：B解：由题意，第二个质点相位落后第一个质点相位π/2，因此，第二个质点的初相位为π21-α，所以答案应选取B 。
2．劲度系数分别为k 1和k 2的两个轻弹簧串联在一起，下面挂着质量为m 的物体，构成一个竖挂的弹簧振子，则该系统的振动周期为 ［ ］（A ）21212)(2k k k k m T +π=； （B ）)(221k k mT +π= ；（C ） 2121)(2k k k k m T +=π； （D ）2122k k mT +π=。
答案：C解：两根弹簧串联，其总劲度系数2121k k k k k +=，根椐弹簧振子周期公式，k mT π2=，代入2121k k k k k +=可得答案为C 。
3．一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上，（如图所示），作成一复摆．已知细棒绕通过其一端的轴的转动惯量231ml J =，此摆作微小振动的周期为 ［ ］ （A ）g l π2； （B ）g l 22π； （C ）g l 322π； （D ）gl 3π。
答案：C解：由于是复摆，其振动的周期公式为glmgl J T 322222πππ===ω，所以答案为C 。
4．一个质点作简谐振动，振幅为A ，在起始时刻质点的位移为A 21，且向x 轴的正方向运动，代表此简谐振动的旋转矢量图为［ ］ 答案：B解：根椐题意，此简谐振动的初相位为3π-，或35π，所以答案为B 。
机械振动课后习题答案机械振动是力学中的一个重要分支，研究物体在受到外力作用后的振动特性。
在学习机械振动的过程中，课后习题是巩固知识、提高能力的重要途径。
本文将为大家提供一些机械振动课后习题的答案，希望能够帮助大家更好地理解和掌握这一知识。
1. 一个质量为m的弹簧振子在无阻尼情况下振动，其振动方程为mx'' + kx = 0，其中x为振子的位移，k为弹簧的劲度系数。
试求振动的周期。
解答：根据振动方程可知，振子的振动是简谐振动，其周期T与振子的质量m和弹簧的劲度系数k有关。
根据简谐振动的周期公式T = 2π√(m/k)，可得振动的周期为T = 2π√(m/k)。
2. 一个质量为m的弹簧振子在受到外力F(t)的作用下振动，其振动方程为mx''+ kx = F(t)，其中F(t) = F0cos(ωt)。
试求振动的解析解。
解答：根据振动方程可知，振子的振动是受迫振动，其解析解可以通过求解齐次方程和非齐次方程得到。
首先求解齐次方程mx'' + kx = 0的解xh(t)，得到振子在无外力作用下的自由振动解。
然后根据外力F(t)的形式，假设其特解为xp(t) = Acos(ωt + φ)，其中A为振幅，φ为相位差。
将特解xp(t)代入非齐次方程，求解得到A和φ的值。
最后，振动的解析解为x(t) = xh(t) + xp(t)。
3. 一个质量为m的弹簧振子在受到阻尼力和外力的作用下振动，其振动方程为mx'' + bx' + kx = F(t)，其中b为阻尼系数。
试求振动的稳定解。
解答：根据振动方程可知，振子的振动是受到阻尼力和外力的作用，其稳定解可以通过求解齐次方程和非齐次方程得到。
首先求解齐次方程mx'' + bx' + kx = 0的解xh(t)，得到振子在无外力和阻尼作用下的自由振动解。
然后根据外力F(t)的形式，假设其特解为xp(t) = Acos(ωt + φ)，其中A为振幅，φ为相位差。
©物理系_2015_09《大学物理AII 》作业 No.01 机械振动班级 ________ 学号 ________ 姓名 _________ 成绩 _______一、 判断题：（用“T ”表示正确和“F ”表示错误）1/3/5 2 4[ F ] 1．只有受弹性力作用的物体才能做简谐振动。
解：如单摆在作小角度摆动的时候也是简谐振动，其回复力为重力的分力。
[ F ] 2．简谐振动系统的角频率由振动系统的初始条件决定。
解：P5. 根据简谐振子角频率公式mk=ω，可知角频率是一个完全由振动系统本身性质决定的常量，与初始条件无关。
我们也将角频率称为固有角频率。
[ F ] 3．单摆的运动就是简谐振动。
解：P14-15 单摆小角度的摆动才可看做是简谐振动。
[ T ] 4．孤立简谐振动系统的动能与势能反相变化。
解：P9 孤立的谐振系统 机械能守恒，动能势能反相变化。
[ F ] 5．两个简谐振动的合成振动一定是简谐振动。
解: 同向不同频率的简谐振动的合成结果就不一定是简谐振动。
总结：1、3、5小题均为简谐振动的定义性判断.简谐运动是最基本也是最简单的一种机械振动。
当某物体进行简谐运动时，物体所受的力跟位移成正比，并且力总是指向平衡位置。
二、选择题：1. 把单摆从平衡位置拉开，使摆线与竖直方向成一微小角度θ，然后由静止放手任其振动，从放手时开始计时。
若用余弦函数表示其运动方程，则该单摆振动的初相位为[ C ] (A) θ; (B) π23; (C) 0; (D) π21。
解：对于小角度摆动的单摆，可以视为简谐振动，其运动方程为：()()0cos ϕωθθ+=t t m ，根据题意，t = 0时，摆角处于正最大处，θθ=m，即：01cos cos 0000=⇒=⇒==ϕϕθϕθθ。
类似公式： ()()0cos ϕω+=t A t x2．一个简谐振动系统，如果振子质量和振幅都加倍，振动周期将是原来的 [D] (A) 4倍(B) 8倍(C) 2倍(D)2倍解： P5 公式(12.1.8) m T k m T m k T ∝⇒=⇒⎪⎭⎪⎬⎫==/2/2πωωπ,所以选D 。
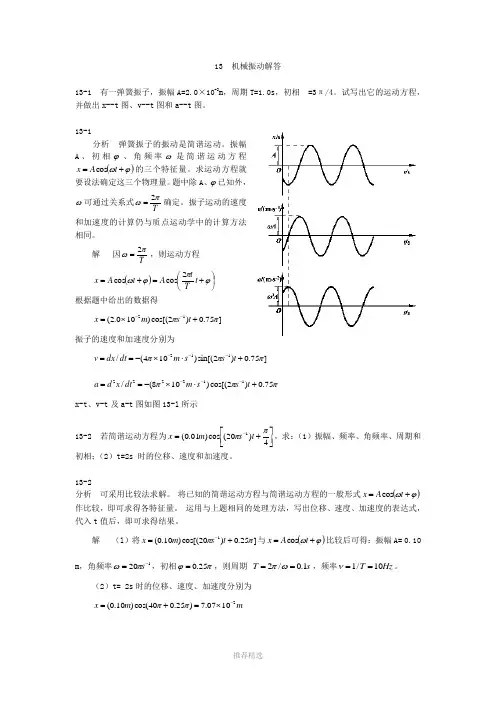
13 机械振动解答13-1 有一弹簧振子，振幅A=2.0×10-2m ，周期T=1.0s ，初相=3π/4。
试写出它的运动方程，并做出x--t 图、v--t 图和a--t 图。
13-1分析 弹簧振子的振动是简谐运动。
振幅A 、初相ϕ、角频率ω是简谐运动方程()ϕω+=t A x cos 的三个特征量。
求运动方程就要设法确定这三个物理量。
题中除A 、ϕ已知外，ω可通过关系式Tπω2=确定。
振子运动的速度和加速度的计算仍与质点运动学中的计算方法相同。
解 因Tπω2=，则运动方程()⎪⎭⎫⎝⎛+=+=ϕπϕωt T t A t A x 2cos cos根据题中给出的数据得]75.0)2cos[()100.2(12ππ+⨯=--t s m x振子的速度和加速度分别为 ]75.0)2sin[()104(/112πππ+⋅⨯-==---t s s m dt dx vπππ75.0)2cos[()108(/112222+⋅⨯-==---t s s m dt x d ax-t 、v-t 及a-t 图如图13-l 所示13-2 若简谐运动方程为⎥⎦⎤⎢⎣⎡+=-4)20(cos )01.0(1ππt s m x ，求：（1）振幅、频率、角频率、周期和初相；（2）t=2s 时的位移、速度和加速度。
13-2分析 可采用比较法求解。
将已知的简谐运动方程与简谐运动方程的一般形式()ϕω+=t A x cos 作比较，即可求得各特征量。
运用与上题相同的处理方法，写出位移、速度、加速度的表达式，代入t 值后，即可求得结果。
解 （l ）将]25.0)20cos[()10.0(1ππ+=-t s m x 与()ϕω+=t A x cos 比较后可得：振幅A= 0.10 m ，角频率120-=s πω，初相πϕ25.0=，则周期 s T 1.0/2==ωπ，频率Hz T 10/1==ν。
（2）t= 2s 时的位移、速度、加速度分别为mm x 21007.7)25.040cos()10.0(-⨯=+=ππ)25.040sin()2(/1πππ+⋅-==-s m dt dx v )25.040cos()40(/2222πππ+⋅-==-s m dt x d a13-3 设地球是一个半径为R 的均匀球体，密度ρ5.5×103kg •m -3。
机械振动学试题（参考答案）一、判断题：（对以下论述，正确的打“J”，错误的打“X”，每题2 分，共20分）1、多自由度振动系统的运动微分方程组中，各运动方程间的耦合，并不是振动系统的固有性质，而只是广义坐标选用的结果。
（丁）2、一个单盘的轴盘系统，在高速旋转时，由于盘的偏心质量使轴盘做弓形回旋时，引起轴内产生交变应力，这是导致在临界转速时，感到剧烈振动的原因。
（X）3、单自由度线性无阻尼系统的自由振动频率由系统的参数确定，与初始条件无关。
（丁）4、当激振力的频率等于单自由度线性阻尼系统的固有频率时，其振幅最大值。
（X）5、一个周期激振力作用到单自由度线性系统上，系统响应的波形与激振力的波形相同，只是两波形间有一定的相位差。
（X）6、当初始条件为零，即*产；=0时，系统不会有自由振动项。
（X）7、对于多自由度无阻尼线性系统，其任何可能的自由振动都可以被描述为模态运动的线性组合。
（丁）8、任何系统只有当所有自由度上的位移均为零时，系统的势能才可能为零。
（X ）9、隔振系统的阻尼愈大，则隔振效果愈好。
（X）10、当自激振动被激发后，若其振幅上升到一定程度并稳定下来，形成一种稳定的周期振动，则这种振幅自稳定性，是由于系统中的某些非线性因素的作用而发生的。
（J）二、计算题：1、一台面以f频率做垂直正弦运动。
如果求台面上的物理保持与台面接触，则台面的最大振幅可有多大？（分）解：台面的振动为：x = X sin（tyZ - cp）x = —a>2X sin（or —cp）最大加速度：无max = "X如台面上的物体与台面保持接触，贝U ：九《=g （9・81米/秒2）。
所以，在f 频率（/=仝）时，最大振幅为：2nX max =x< g/4^72= 9.81/4* 严（米）2、质量为ni 的发电转子，它的转动惯量J 。
的确定采用试验方法：在转子经向Ri 的 地方附加一小质量mi 。
试验装置如图1所示，记录其振动周期。
一、选择题：1．3001：把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度θ ，然后由静止放手任其振动，从放手时开始计时。
若用余弦函数表示其运动方程，则该单摆振动的初相为(A) π (B) π/2 (C) 0 (D) θ ［ ］2．3002：两个质点各自作简谐振动，它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(ωt + α)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处。
则第二个质点的振动方程为：(A))π21cos(2++=αωt A x (B) )π21cos(2-+=αωt A x (C))π23cos(2-+=αωt A x (D) )cos(2π++=αωt A x ［ ］3．3007：一质量为m 的物体挂在劲度系数为k 的轻弹簧下面，振动角频率为ω。
若把此弹簧分割成二等份，将物体m 挂在分割后的一根弹簧上，则振动角频率是(A) 2 ω (B) ω2 (C) 2/ω (D) ω /2 ［ ］4．3396：一质点作简谐振动。
其运动速度与时间的曲线如图所示。
若质点的振动规律用余弦函数描述，则其初相应为 (A) π/6 (B) 5π/6 (C) -5π/6 (D) -π/6 (E) -2π/3 v 与a5．3552期分别为T 1和T 2。
将它们拿到月球上去，相应的周期分别为1T '和2T '。
则有(A) 11T T >'且22T T >' (B) 11T T <'且22T T <'(C) 11T T ='且22T T =' (D) 11T T ='且22T T >'［ ］ 6．5178：一质点沿x 轴作简谐振动，振动方程为)312cos(1042π+π⨯=-t x (SI)。
从t = 0时刻起，到质点位置在x = -2 cm 处，且向x 轴正方向运动的最短时间间隔为(A) s 81 (B) s 61 (C) s 41 (D) s 31 (E)［ ］7．5179：一弹簧振子，重物的质量为m ，弹簧的劲度系数为k ，该振子作振幅为A 的简谐振动。
