遗传算法与分枝定界法求解TSP研究

实验六：遗传算法求解TSP问题实验2篇第一篇：遗传算法的原理与实现1. 引言旅行商问题（TSP问题）是一个典型的组合优化问题，它要求在给定一组城市和每对城市之间的距离后，找到一条路径，使得旅行商能够在所有城市中恰好访问一次并回到起点，并且总旅行距离最短。

遗传算法作为一种生物启发式算法，在解决TSP问题中具有一定的优势。

本实验将运用遗传算法求解TSP问题，以此来探讨和研究遗传算法在优化问题上的应用。

2. 遗传算法的基本原理遗传算法是模拟自然界生物进化过程的一种优化算法。

其基本原理可以概括为：选择、交叉和变异。

（1）选择：根据问题的目标函数，以适应度函数来评估个体的优劣程度，并按照适应度值进行选择，优秀的个体被保留下来用于下一代。

（2）交叉：从选出的个体中随机选择两个个体，进行基因的交换，以产生新的个体。

交叉算子的选择及实现方式会对算法效果产生很大的影响。

（3）变异：对新生成的个体进行基因的变异操作，以保证算法的搜索能够足够广泛、全面。

通过选择、交叉和变异操作，不断迭代生成新一代的个体，遗传算法能够逐步优化解，并最终找到问题的全局最优解。

3. 实验设计与实施（1）问题定义：给定一组城市和每对城市之间的距离数据，要求找到一条路径，访问所有城市一次并回到起点，使得旅行距离最短。

（2）数据集准备：选择适当规模的城市数据集，包括城市坐标和每对城市之间的距离，用于验证遗传算法的性能。

（3）遗传算法的实现：根据遗传算法的基本原理，设计相应的选择、交叉和变异操作，确定适应度函数的定义，以及选择和优化参数的设置。

（4）实验流程：a. 初始化种群：随机生成初始种群，每个个体表示一种解（路径）。

b. 计算适应度：根据适应度函数，计算每个个体的适应度值。

c. 选择操作：根据适应度值选择一定数量的个体，作为下一代的父代。

d. 交叉操作：对父代进行交叉操作，生成新的个体。

e. 变异操作：对新生成的个体进行变异操作，以增加搜索的多样性。

基于遗传算法的TSP问题研究旅行商问题（TSP）是一类NP-hard（非确定性的可能时间指数）问题，涉及到寻找一条最短的路径，以便走遍一系列的城市。

这个问题的例子就像是一个推销员想要在多个城市中寻找到一条能够使他成本最小化并且每个城市只访问一次的路径。

由于旅行商问题的困难度，许多学者和研究者致力于寻找最优解决方案。

在过去的几十年中，各种各样的算法被提出来，其中之一就是遗传算法。

遗传算法的基本原理是模仿自然界中的进化过程。

在这个算法中，候选解决方案根据它们与当前已知最优解的接近情况来进行繁殖和变异。

这种方法通过不断迭代，逐步优化了解决方案。

在TSP领域中，遗传算法已经得到了广泛的应用。

这是因为算法简单易懂，且计算速度快。

但是，它也存在一些缺点。

首先，它对最初种群的设定敏感，因为遗传算法的结果取决于初始的种群。

此外，算法可能会在局部最优解中陷入困境，而无法到达全局最优解。

虽然这些问题存在，但仍有许多研究者尝试改进遗传算法，以提高其效率和准确性。

例如，有些人将变异率设为自适应的变量，以在迭代初期增加变异率，并在迭代后期逐渐减少变异率，以便更好地优化解决方案。

同时，其他一些研究者正在尝试将遗传算法与其他的优化算法相结合，以便更好地解决TSP问题。

特别是，一些研究者使用了禁忌搜索方法，将其与遗传算法结合使用，以避免算法在局部最优解中停滞不前。

总的来说，基于遗传算法的TSP问题研究取得了一些非常有意义的成果。

尽管仍有许多问题需要解决，但这种方法在解决TSP问题中仍然是一种非常有前途的方法。

我们期待在日后的研究中看到更多有关这种算法的创新，以期能够找到真正有效的解决方法。

遗传算法求解TSP问题⼀、简介遗传算法是基于达尔⽂的⽣物进化论，是⼈⼯智能算法的的重要分⽀，主要⽤于解决⼀类求最优解问题。

如旅⾏商（TSP）问题。

遗传算法是将状态当成染⾊体，状态⾥的每⼀个决策都是染⾊体上的⼀个基因。

然后根据实际情况⽣成⼀个适应度函数，计算每⼀串染⾊体对环境的适应度。

让适应度⾼的遗传到下⼀代，适应度低的淘汰掉，另外在实现的过程中也许会发⽣变异，导致⼀些决策改变。

除此之外，遗传算法是随机性近似算法，所以当我们运⽤该算法时必须采取措施使其收敛到全局最优解，并且尽量提⾼达到最优解的概率。

遗传算法除了设计适应度函数以外，还有很重要的三个部分：选择，交叉，变异。

⼆、遗传算法实现步骤1.评估每条染⾊体所对应个体的适应度。

2.遵照适应度越⾼，选择概率越⼤的原则，从种群中选择两个个体作为⽗⽅和母⽅。

3.抽取⽗母双⽅的染⾊体，进⾏交叉，产⽣⼦代。

4.对⼦代的染⾊体进⾏变异。

5.重复2，3，4步骤，直到新种群的产⽣。

三、遗传算法求解TSP实现步骤1.确定影响因素城市序列、城市个数N、种群个数M、交叉概率Pc、变异概率Pmutation等；2.初始化数据2.1初始化影响因素：城市序列、城市个数N、种群个数M、交叉概率Pc、变异概率Pmutation2.2 初始化数据：读⼊数据源，将坐标转换为距离矩阵（标准化欧式距离）3.计算种群适应度已知任意两个城市之间的距离，每个染⾊体可计算出总距离，因此可以将⼀个随机全排列的总距离的倒数作为适应度函数，即距离越短，适应度函数越好。

4.迭代选择算⼦：赌轮选择策略挑选下⼀代个体。

交叉运算：在交叉概率的控制下，对群体中的个体两两进⾏交叉。

变异运算：在变异概率的控制下，对群体中的个体两两进⾏变异，即对某⼀个体的基因进⾏随机调整。

计算新的种群适应度以及个体累积概率，并更新最优解。

将新种群复制到旧种群中，准备下⼀代进化（迭代）。

5.输出输出迭代过程中产⽣的最短路径长度以及最短路径。

遗传算法求解TSP问题实验六遗传算法求解TSP问题⼀、实验⽬的熟悉和掌握遗传算法的原理、流程和编码策略，并利⽤遗传求解函数优化问题，理解求解TSP问题的流程并测试主要参数对结果的影响。

⼆、实验内容1、参考实验系统给出的遗传算法核⼼代码，⽤遗传算法求解TSP的优化问题，分析遗传算法求解不同规模TSP问题的算法性能。

2、对于同⼀个TSP问题，分析种群规模、交叉概率和变异概率对算法结果的影响。

3、增加1种变异策略和1种个体选择概率分配策略，⽐较求解同⼀TSP问题时不同变异策略及不同个体选择分配策略对算法结果的影响。

4、上交源代码。

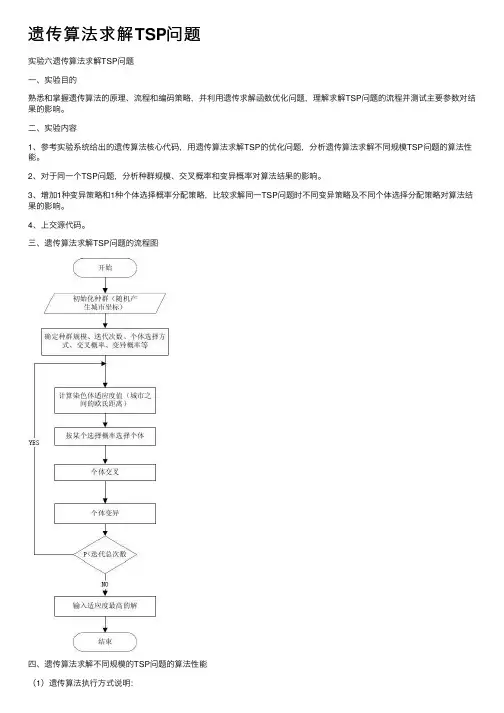
三、遗传算法求解TSP问题的流程图四、遗传算法求解不同规模的TSP问题的算法性能（1）遗传算法执⾏⽅式说明：适应度值计算⽅法：当前路线的路径长度●个体选择概率分配⽅法：适应度⽐例⽅法●选择个体⽅法：轮盘赌选择●交叉类型：PMX交叉●变异类型: 两点互换变异（2）实验模拟结果：图1-1（3）分析由图1-1可知，遗传算法执⾏时间随着TSP问题规模的增⼤⽽增⼤，并且⼤致为线性增长。

五、不同参数下的计算结果对⽐最⼤迭代步数:100交叉概率：0.85变异概率：0.15如表1-1或3-1-0-9-2-4-8-5-7-6，注意到这是⼀圈，顺时针或者逆时针都可以。

当种群规模为10，20时，并没有找到最优解。

（2）交叉概率对算法结果的影响实验次数：15种群规模：25最⼤迭代步数:100变异概率：0.15实验结果：在该情况下，交叉概率过低将使搜索陷⼊迟钝状态，得不到最优解。

种群规模：25最⼤迭代步数:100交叉概率：0.85实验结果：⼜表1-3可知，当变异概率过⼤或过低都将导致⽆法得到最优解。

注：（2）（3）的实验数据与（1）的实验数据不同，详见附录。

六、不同变异策略和个体选择概率分配策略对算法结果的影响（1）两点互换变异与插⼊变异的⽐较：●试验次数（CASNUM）：10●城市数(POINTCNT):10●种群规模(POPSIZE)：100●最⼤迭代步数(GENERATIONS):100●交叉概率(PC)：0.85●变异概率(PM):0.15●选择个体⽅法：轮盘赌选择●交叉类型：PMX交叉●个体选择概率分配⽅法：适应度⽐例⽅法a.变异类型: 两点互换变异b.变异类型: 插⼊变异分析：两点互换变异20次模拟中，4次得到⾮最优解；⽽插⼊变异只有2次；插⼊变异的最好适应度平均值⽐两点互换变异⼩0.14755，最差适应度平均值和总的适应度平均值都⽐两点互换下，并且在Release下，运⾏时间前者⽐后者快218.3ms。

科技论坛引言：旅行推销商问题（Traveling Salesman Problem，简记TSP）是最有代表性的优化组合问题之一，它的应用已渗透到各技术领域。

TSP会产生所谓“组合爆炸”问题，行业专家相继提出了各种方法来解决这个问题。

近年来，神经网络，退火算法，蚁群算法，遗传算法等典型的不完全算法与TSP问题相结合，促进了TSP问题的解决。

而遗传算法又以其简单性、高效性和强鲁棒性等优点，成为了解决TSP问题的重要方法之一。

1TSP问题TSP问题是由威廉·哈米尔顿爵士和英国数学家克克曼于19世纪初提出的一个数学问题[1]。

可以简单描述为：一个推销员欲到n个城市销售商品，从城市1出发，经过其余各城市一次且仅仅一次，然后回到出发点，问如何选择一条路径才使得销售员的行程最短。

也即是寻找一条巡回路径T=（t1，…，t i，…t n），使得函数f（T）的值最小，如下式所示：f（T）=n-1i=1Σd（t i，t i+1）+d（t n，t1）其中，t i为城市标号为i的城市，d（t i，t j）表示城市i和城市j之间的距离，i∈[1，n]。

人们在考虑解决TSP问题时，首先想到的一种方法就是：列出每一条可供选择的路线，计算出每条路线的总里程，最后从中选出一条最短的路线。

很显然，当城市数目不多时要找到最短距离的路线并不难，但随着城市数目的不断增大，组合路线数将呈n成指数级数急剧增长，以至达到无法计算的地步，这就是所谓的“组合爆炸”问题。

因此，TSP虽然容易描述，但找出其最优解却是非常困难的。

目前人们主要采用仿生学算法、启发式算法等现代优化算法，试图在一定条件下找到TSP问题的理想解。

其中遗传算法因为其简单性、高效性和强鲁棒性等优点，成为解决TSP问题的有效方法之一[2-3]。

2遗传算法2.1遗传算法简介。

遗传算法（Genetic Al－gorithm）是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法，它是由美国Michi－gan大学J.Holland教授于1975年首先提出来的[1，4-5]。

北京工业大学硕士学位论文用一种免疫遗传算法求解MST、TSP问题姓名：***申请学位级别：硕士专业：运筹学与控制论指导教师：***20040501摘要遗传算法是借鉴生物的自然选择和遗传化机制而开发出的一种全局优化自适应概率搜索算法，它更表现出比其他传统优化方法更加独特和优越的性能，隐含并行性和全局搜索特点是遗传算法的两大显著特征，因此关于遗传算法的研究越来越受到重视。

考虑到遗传算法中选择和交叉算子对群体多样性的影响，本文进一步明确遗传算法存在易陷入早熟收敛和后期收敛速度慢的缺点。

正是由于考虑到选择和交叉算子对算法的多样性影响，改进选择算子和交叉算子是本文主要关注的两个问题。

人体免疫功能的特点对于改进和提高遗传算法的能力是十分有启迪性的．本文在选择算予改进上不仅考虑适应度概率来选择，并加入浓度概率来加以选择，这样既确保了适应度高的个体能传到下一代，同时也保持了群体的多样性。

同时考虑算子的可行性和效率，采用了矢量距浓度概率的计算；在交叉算子设计上，为了避免多样性由交叉而丢失，采用的交叉算子应尽量减少由交叉所得群体中相似个体的比例；同时采用了最优保持策略，有益于群体多样性的保持。

图论是数学中有广泛实际应用的一个分支，其中典型问题包括：ＭＳＴ、ＴＳＰ问题。

本文以图论中ＭＳＴ、ＴＳＰ问题为例，以改进的遗传算法来求解，取得较好的结果；关键词：遗传算法免疫多样性交叉ＡｂｓｔｒａｃｔＧｅｎｅｔｉｃＡｌｇｏｒｉｔｈｍ（ＧＡ）ｉｓａｎａｄａｐｔａｂｌｅｐｒｏｂａｂｉｌｉｔｙｓｅａｒｃｈａｌｇｏｒｉｔｈｍｔｈａｔｉｓｃｒｅａｔｅｄｔｈｒｏｕｇｈａｄａｐｔａｔｉｏｎｉｎＮａｔｕｒｅａｎｄｒｏｌｅｏｆＧｅｎｅｔｉｃｓ．Ｉｔｈａｓｓｕｐｅｒｉｏｒｔｏｏｔｈｅｒｃｏｎｖｅｎｔｉｏｎａｌｏｐｔｉｍｉｚａｔｉｏｎａｌｇｏｒｉｔｈｍｉｎｓｐｅｃｉａｌｉｚｅｄｑｕａｌｉｔｙ．ＩｍｐｌｉｃｉｔｐａｒａｌｌｅｌａｎｄｇｌｏｂａｌｓｅａｒｃｈｉｎｇａｒｅｔｗｏｒｅｍａｒｋａｂｌｅｃｈａｒａｃｔｅｒｉｓｔｉｃｓｏｆＧＡ．ＴｈｅｓｔｕｄｙｏｆＧＡｉｓｇｅｔｔｉｎｇｍｏｒｅａｎｄｍｏｒｅａｔｔｅｎｔｉｖｅ．ＢｅｃａｕｓｅｔｈｅｓｅｌｅｃｔｉｎｇａｎｄｃｒｏｓｓｏｖｅｒｏｐｅｒａｔｉｏｎｓｉｎＧＡｐｌａｙａｓｉｇｎｉｆｉｃａｎｔｒｏｌｅｉｎＧＡ，ｔｈｉｓｐａｐｅｒｆｕｒｔｈｅｒｓｈｏｗｓｔｈａｔＧＡｈａｓｔｗｏｄｅｆｉｃｉｅｎｃｉｅｓ：ｐｒｅｍａｔｕｒｅｃｏｎｖｅｒｇｅｎｃｅａｎｄｓｌｏｗｃｏｎｖｅｒｇｅｎｃｅｓｐｅｅｄｉｎｌａｔｅｒｐｈｒａｓｅ．Ｓｏｔｈｉｓｐａｐｅｒｔａｋｅｓｍｏｒｅａｔｔｅｎｔｉｏｎｔｏｓｅｌｅｃｔａｎｄｃｒｏｓｓｏｖｅｒｏｐｅｒａｔｉｏｎｓ．ＩｍｍｕｎｅｑｕａｌｉｔｙｈａｓａｇｏｏｄｅｄｉｆｉｃａｔｏｒｙｅｆｆｅｃｔｉｎｉｍｐｒｏｖｉｎｇＧＡ．Ｉｎｔｈｉｓｐａｐｅｒｗｅｃｏｎｓｉｄｅｒｔｈａｔｃｈｏｏｓｉｎｇｏｐｅｒａｔｉｏｎａｃｔｓｂｙｂｏｔｈａｄａｐｔｐｒｏｂａｂｉｌｉｔｙａｎｄｃｏｎｃｅｎ订ａｔｉｏｎｐｒｏｂａｂｉｌｉｔｙ，ｓｏｉｔｃａｎａｓｓｕｒｅｔｈａｔｃｈｒｏｍｏｓｏｍｅｗｉｔｈｈｉｇｈｅｒａｄａｐｔａｂｉｌｉｔｙｃａｎｂｅｇｏｒｏｕｎｄｔｏｔｈｅｎｅｘｔｇｅｎｅｒａｔｉｏｎ．Ｍｅａｎｗｈｉｌｅｉｔｒｅｔａｉｎｓｃｏｌｏｎｙｄｉｖｅｒｓｉｔｙ．Ｉｎｅｖａｌｕａｔｉｎｇｃｈｒｏｍｏｓｏｍｅｃｏｎｃｅｎｔｒａｔｉｏｎ，ａｎｅｗｃｏｎｃｅｎｔｒａｔｉｏｎｐｒｏｂａｂｉｌｉｔｙｍｅｔｈｏｄｉｓｕｓｅｄ．Ｉｎｃｒｏｓｓｏｖｅｒｏｐｅｒａｔｉｏｎ，ｉｎｏｒｄｅｒｔｏａｖｏｉｄｄｉｖｅｒｓｉｔｙｌｏｓｉｎｇｂｙｃｒｏｓｓｏｖｅＬｗｅｓｈｏｕｌｄｒｅｄｕｃｅｓｉｍｉｌａｒｃｈｒｏｍｏｓｏｍｅｐｅｒｃｅｎｔａｇｅｔｈｒｏｕ曲ｅｍｐｌｏｙｉｎｇｓｐｅｃｉａｌｃｒｏｓｓｏｖｅｒｏｐｅｒａｔｏｒｔｏｔｈｅｑｕｅｓｔｉｏｎ．Ｃｌａｓｓｉｃｉｎｄｉｖｉｄｕａｌｒｅｓｅｒｖａｔｉｏｎｉｓｂｅｎｅｆｉｃｉａｌｔｏｋｅｅｐｃｏｌｏｎｙｄｉｖｅｒｓｉｔｙ．Ｇｒａｐｈｔｈｅｏｒｙｉｓａｂｒａｎｃｈｏｆｍａｔｈｅｍａｔｉｃｓ，ｗｈｉｃｈｈａｓｅｘｔｅｎｓｉｖｅａｐｐｌｉｃａｔｉｏｎ．ＩｎＧｒａｐｈｔｈｅｏｒｙｔｙｐｉｃａｌｐｒｏｂｌｅｍｓｉｎｃｌｕｄｅＭＳＴａｎｄＴＳＥＴｈｉｓｐａｐｅｒｕｓｅｓｉｍｐｒｏｖｅｄＧＡｔｏｓｅｅｋａｎｓｗｅｒｓｔｏｔｈｅｔｗｏｑｕｅｓｔｉｏｎｓ，ｇａｉｎｉｎｇｂｅｔｔｅｒａｎｓｗｅｒｓ．ＫｅｙＷｏｒｄｓ：ＧｅｎｅｔｉｃＡｌｇｏｒｉｔｈｍｓ；Ｉｍｍｕｎｅ；Ｄｉｖｅｒｓｉｔｙ；Ｃｒｏｓｓｏｖｅｒ．独创性声踢本人声明所呈交的论文是我个人在导师指导下进行的研究工作及取得的研究成果．尽我所知，除了文中特别加以标注和致谢的地方外，论文中不包含其他人已经发表或撰写过的研究成果，也不包含为获得北京工业大学或其它教育饥构的学位或证书面使用过的材料．与我一同工作的同志对本研究所做的任何贡献均已在论文中作了明确的说明并表示了谢意．签名缓盔Ｈ＆日期：兰竺芏！』：墨关于论文使用授权的说明本人完全了解北京工业大学有关保留、使用学位论文的规定，即：学校有权保留送交论文的复印件，允许论文被查阅和借阅；学校可以公布论文的全部或部分内容，可以采用影印、缩印或其他复制手段保存论文．（保密的论文在解密后应遵守此规定）签名：二垂继导师签名；ｊ数日期ｂ坤．占第１章绪论基本遗传算法是一种新兴的优化算法，它有其很多的优点，为许多领域带来了全新的概念和解决思路；但基本遗传算法也有其弊端和不足，这篇文章主要想改进一般遗传算法，考虑到遗传算法是一新的算法，首先我们从介绍遗传算法开始。

基于遺传算法的TSP问题研究摘要：旅行商问题是一个经典的优化组合问题，本文采用遗传算法来求解旅行商问题，深入讨论了遗传算法解决TSP问题的求解过程，并通过MATLAB对算法进行了实现，最后对实验结果进行分析。

关键字：旅行商问题；遗传算法Abstract:The traveling salesman problem is a classic optimal combination problem. In this paper, we use genetic algorithm to solve the TSP problem. We discusse the solving process, and the algorithm is realized by MATLAB. Finally, the experimental results are analyzed.Key words: Traveling Salesman Problem; Genetic Algorithm1引言旅行商问题(Trave 1 i ng Sa 1 esman Problem,TSP)的原始问题为：一个商人欲到n个城市推销商品，每两个城市i和j之间的距离为〃如何选择一条道路使得商人每个城市正好走一遍后回到起点且所走路线最短。

这是一个经典的优化组合问题，它可以扩展到很多问题，如电路布线、输油管路铺设等，但是，由于TSP问题的可行解数目与城市数目N是成指数型增长的»是一个NP-hard问题»即不存在多项式时间算法。

因而一般只能近似求解，遗传算法(Genetic Algorithm,GA)是求解该问题的较.有效的方法之一，当然还有如粒子群算法，蚁群算法，神经网络算法等优化算法也可以进行求解。

遗传算法是美国学者Holland根据自然界“物竞天择，适者生存”现象而提出的一种随机搜索算法，本文采用MATLAB来实现遗传算法解决TSP问题。

现代优化计算方法研究报告——遗传算法解决TSP问题授课老师：专业：学号：姓名：摘要旅行商问题（TSP）是典型的NP完全问题，遗传算法是解决NP完全问题的一种常用算法。

本文首先简要介绍了TSP问题和遗传算法，然后用遗传算法对TSP问题进行了求解，并在MATLAB上进行了编程实现。

最后探讨了遗传算法解决TSP问题的一些特点。

关键词：TSP问题；遗传算法；MATLAB目录摘要 (2)目录 (3)1 旅行商问题 (4)1.1 旅行商问题简介 (4)1.2 TSP的数学描述 (4)2 遗传算法 (4)2.1 遗传算法简介 (4)2.2 遗传算法的步骤 (5)3 遗传算法求解TSP问题 (5)3.1 初始群体和适应度函数 (6)3.2 城市的位置和城市间的距离 (6)3.3 交叉和变异 (6)3.4 种群的更新和迭代终止条件 (6)4 MATLAB仿真以及运行结果 (7)5 总结 (7)附件——MATLAB程序代码 (8)1 旅行商问题1.1 旅行商问题简介旅行商问题（traveling salesman problem,TSP ）是一个有名的、典型的、易于描述却难以求解的组合优化问题。

TSP 已被证明具有NPC 计算复杂性，并且许多实际问题都可以转化为TSP 。

它是一个具有广泛的实用背景和重要的理论价值的组合优化难题。

1.2 TSP 的数学描述一个商人欲到n 个城市推销商品，每两个城市i 和j 之间的距离为ij d ，如何选择一条道路使得商人每个城市走一遍后回到起点且所走路径最短？ TSP 可以细分为对称和非对称距离两大类问题。

当j i d d ji ij ,,∀=时，称为对称距离TSP ，否则为飞对称距离TSP 。

对于一般的TSP ，一种数学模型描述为∑≠ji ij ij x d min （1-1）∑===n j ij n i xt s 1,,2,1,1.. （1-2） ∑===ni ij n j x1,,2,1,1 （1-3） ∑∈⊂-≤≤-≤S j i ij n S n S S x ,},,2,1{,2||2,1|| （1-4）j i n j i x ij ≠=∈,,,1,},1,0{ （1-5）以上是基于图论的数学模型，其中式（1-5）中的决策变量1=ij x 表示商人行走的路线包含从城市i 到城市j 的路径，0=ij x 表示商人没有选择走这条路。

文章编号:1009-4873(2008)04-0040-03遗传算法在求解TSP 问题上的应用刘 渊1, 郝丽宁2(1.石家庄铁路职业技术学院信息工程系,河北石家庄 050041;2.河北经贸大学商学院,河北石家庄 050061)摘 要:论述了遗传算法在编码表示和遗传算子等方面的应用情况,指出了常用编码方法的优点和缺点,并且结合T SP 的运行实例详细分析了基本遗传算法对求解结果和求解效率的影响.简单说明了混合遗传算法在求解T SP 问题中的应用并对遗传算法解决T SP 问题的前景提出了展望.关键词:T SP;遗传算法;遗传算子;编码中图分类号:O22 文献标识码:A现代科学理论研究与实践中存在着大量的与优化、自适应相关的问题,但除了一些简单的情况之外,人们对于大型复杂系统的优化和自适应问题仍然无能为力。

遗传算法正是借鉴生物的自然选择和遗传进化机制而开发出的一种全局优化的自适应概率搜索算法。

遗传算法在T SP 问题求解方面的应用研究,对于构造合适的遗传算法框架、建立有效的遗传操作以及有效地解决T SP 问题等有重要意义。

1 TSP 问题T SP 问题也称为巡回旅行商问题,是一个古老的问题.最早可以追溯到1759年Euler 提出的骑士旅行问题.TSP 问题是一个典型的、容易描述但是难以处理的NP 完全问题,同时TSP 问题也是诸多领域内出现的多种复杂问题的集中概括和简化形式.所以,有效地解决T SP 问题在计算理论和实际应用上都有很高的价值.2 遗传算法遗传算法是一种借鉴生物界自然选择和自然遗传机制的随机化搜索算法,由美国J.H.Holland 教授提出,其主要特点是群体搜索策略和群体中个体之间的信息交换、搜索不依赖于梯度信息.遗传算法是一种全局化搜索算法,简单、通用、鲁棒性强,尤其适用于传统搜索算法难以解决的复杂和非线性问题.隐含并行性和全局搜索性是遗传算法的两大显著特征.3 遗传算法在TSP 上的应用3.1 TSP 问题的建模与描述TSP 问题属于NP 完全问题,它给定一组n 个城市和他们两两之间的直达距离,寻找一条闭合旅程,使得每个城市刚好经过一次而且总的旅行距离最短.[1]TSP 问题的描述简言之就是寻找一条最短的遍历n 个城市的路径,或者说搜索整数子集X ={1,2, ,n}(X 的元素表示对n 个城市的编号)的一个排列 (X )={v 1,v 2, ,v n },使T =d(v i ,v i+1)+d (v i ,v n )最小.其中,d (v i ,v i+1)表示城市v i 到城市v i+1的距离.3.2 TSP 的遗传基因编码方法在遗传算法的应用中,遗传基因编码是一个很重要的问题.对遗传基因进行编码时,要考虑是否适合或有利于交叉和变异操作.[2]在求解TSP 问题时,Grefenstette 等提出了基于顺序表示的遗传基因编码方法.[3]顺序表示是指所有城市依次排列构成一个顺序表,对于一条旅程,可以依旅行经过顺序处理每个城市,每个城市在顺序表中的顺序就是一个遗传因子的表示,每处理完一个城市,就从顺序表中去掉该城市.处理完所有城市以后,将每个城市的遗传因子表示连接起来,就是一条旅程的基因表示.这种表示方法,在进行单点交叉时,交叉点右侧部分的旅程随即发生变化,但交叉点左侧部分的旅程未发生改变.由于存在这样的缺点,收稿日期:2008-06-20作者简介:刘 渊(1981-),女,河北石家庄人,石家庄铁路职业技术学院教师.2008年8月第20卷第4期石家庄职业技术学院学报Jour nal of Shijiazhuang Vocational T echnolog y Institute Aug.2008V ol.20 No.4所以顺序表示方法的适用性存在一定的问题.[4] 3.3 初始种群的产生产生初始种群的方法通常有两种:一种是完全随机的方法,它适合于对问题的解无任何先验知识的情况;另一种是某些先验知识可转变为必须满足的一组要求,然后在满足这些要求的解中再随机地选取样本,这样选择初始种群可使遗传算法更快地到达最优解.3.4 TSP的遗传操作算子3.4.1 选择算子对于求解TSP问题,常用的选择机制有轮盘赌选择机制、最佳个体保存选择机制、期望值模型机制、排序模型选择机制、联赛选择模型机制和排挤模型等.[5]遗传算法中一个要求解决的问题是如何防止 早熟 收敛现象.为了保证遗传算法的全局收敛性,就要维持群体中个体的多样性,避免有效基因的丢失.Rudolhp C提出采用精英选择策略即保持群体中最好的个体不丢失,以保证算法的收敛性.[5] Konstantin Boukreev采用联赛选择方法和最优个体保存方法相结合的方法.[6]谢胜利提出浓度控制策略,当某种个体的浓度超过给定的浓度阀值时,减少该种个体的数量,使之控制在给定的浓度阀值内,并随机产生新的个体以保证种群的规模.通过实验证明,该策略很好地解决了遗传算法中群体的多样性问题.[7]在该遗传算法中采用的是轮盘赌选择和最佳保存策略选择。