开环对数频率特性和时域指标.
- 格式:doc
- 大小:207.50 KB
- 文档页数:4







5.6 利用开环频率特性分析系统的性能在频域中对系统进行分析、设计时,通常是以频域指标作为依据的,但是不如时域指标来得直接、准确。
因此,须进一步探讨频域指标与时域指标之间的关系。
考虑到对数频率特性在控制工程中应用的广泛性,本节将以Bode 图为基点,首先讨论开环对数幅频特性)(ωL 的形状与性能指标的关系,然后根据频域指标与时域指标的关系估算出系统的时域响应性能。
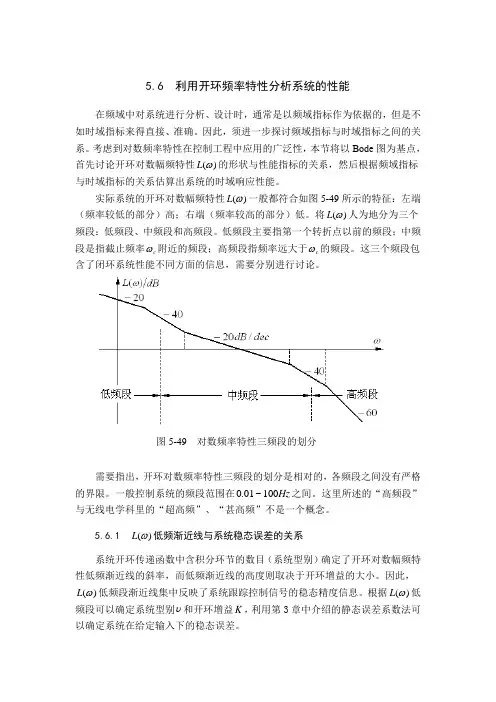
实际系统的开环对数幅频特性)(ωL 一般都符合如图5-49所示的特征:左端(频率较低的部分)高;右端(频率较高的部分)低。
将)(ωL 人为地分为三个频段:低频段、中频段和高频段。
低频段主要指第一个转折点以前的频段;中频段是指截止频率c ω附近的频段;高频段指频率远大于c ω的频段。
这三个频段包含了闭环系统性能不同方面的信息,需要分别进行讨论。
需要指出,开环对数频率特性三频段的划分是相对的,各频段之间没有严格的界限。
一般控制系统的频段范围在Hz 100~01.0之间。
这里所述的“高频段”与无线电学科里的“超高频”、“甚高频”不是一个概念。
5.6.1 )(ωL 低频渐近线与系统稳态误差的关系系统开环传递函数中含积分环节的数目(系统型别)确定了开环对数幅频特性低频渐近线的斜率,而低频渐近线的高度则取决于开环增益的大小。
因此,)(ωL 低频段渐近线集中反映了系统跟踪控制信号的稳态精度信息。
根据)(ωL 低频段可以确定系统型别υ和开环增益K ,利用第3章中介绍的静态误差系数法可以确定系统在给定输入下的稳态误差。
图5-49 对数频率特性三频段的划分5.6.2 )(ωL 中频段特性与系统动态性能的关系开环对数幅频特性的中频段是指截止频率c ω附近的频段。
设开环部分纯粹由积分环节构成,图5-50(a )所示的对数幅频特性对应一个积分环节,斜率为dec dB /20-,相角 90)(-=ωϕ,因而相角裕度 90=γ;图5-50(b )的对数幅频特性对应两个积分环节,斜率为dec dB /40-,相角 180)(-=ωϕ,因而相角裕度 0=γ。

1.控制概念(1)开环控制:开环控制是最简单的一种控制方式。
它的特点是,按照控制信息传递的路径,控制量与被控制量之间只有前向通路而没有反馈通路。
闭环控制:凡是将系统的输出量反送至输入端,对系统的控制作用产生直接的影响,都称为闭环控制系统或反馈控制系统。
复合控制:是开、闭环控制相结合的一种控制方式。
(2)反馈:指将系统的输出返回到输入端并以某种方式改变输入,进而影响系统功能的过程,即将输出量通过恰当的检测装置返回到输入端并与输入量进行比较的过程。
(3)传递函数:在零初始条件下,系统输出信号的拉手变换与输出信号的拉氏变换的比。
(4)被控对象:指需要给以控制的机器、设备或生产过程。
执行机构:一种能提供直线或旋转运动的驱动装置,它利用某种驱动能源并在某种控制信号作用下工作。
(5)线性化:a条件:连续且各阶导数存在 b方法:工作点附近泰勒级数展开。
2.时域指标(1)上升时间tr:响应从终值10%上升到终值90%所需时间;对有振荡系统亦可定义为响应从零第一次上升到终值所需时间。
上升时间是响应速度的度量。
峰值时间tp:响应超过其终值到达第一个峰值所需时间。
调节时间ts:响应到达并保持在终值内所需时间。
(2)超调量σ%:响应的最大偏离量h(tp)与终值h(∞)之差的百分比。
振荡次数:是在阶跃信号作用下,系统在达到指定deta范围下,系统所震荡的总次数。
(3)动态降落:系统稳定运行时,突然加一个扰动量N,在过度过程中引起输出量的最大降落值Cmax称为动态降落。
恢复时间:系统从波动回复到稳态时候所需要的时间。
(4)稳态误差:对单位负反馈系统,当时间t趋于无穷大时,系统对输入信号响应的实际值与期望值(即输入量)之差的极限值,称为稳态误差,它反映系统复现输入信号的(稳态)精度。
3.频域特性(1)频率特性:对于线性系统来说,当输入信号为正弦信号时,稳态时的输出信号是一个与输入信号同频率的正弦信号,不同的只是其幅值与相位,且幅值与相位随输入信号的频率不同而不同。

自动控制原理总经典总结《自动控制原理》总复习控制线性非线连续离散描述函相平面建模-时域法串联(频率法)建模-求稳定性负倒描述函数曲线自振点振幅、频绘制相求奇点和极限环求运动校正第一章 自动控制的基本概念一、学习要点1. 自动控制基本术语:自动控制、系统、自动控制系统、被控量、输入量、干扰量、受控对象、控制器、反馈、负反馈控制原理等。
2. 控制系统的基本方式:①开环控制系统;②闭环控制系统;③复合控制系统。
3. 自动控制系统的组成:由受控对象和控制器组成。
4. 自动控制系统的类型:从不同的角度可以有不同的分法,常有:恒值系统与随动系统;线性系统与非线性系统;连续系统与离散系统;定常系统与时变系统等。
5. 对自动控制系统的基本要求:稳、快、准。
6. 典型输入信号:脉冲、阶跃、斜坡、抛物线、正弦。
二、基本要求1. 对反馈控制系统的基本控制和方法有一个全面的、整体的了解。
2. 掌握自动控制系统的基本概念、术语,了解自动控制系统的组成、分类,理解对自动控制系统稳、准、快三方面的基本要求。
3. 了解控制系统的典型输入信号。
4. 掌握由系统工作原理图画方框图的方法。
三、内容结构图自动控制的由系统工作原对控制系统常用术语、基本控反馈控制系控制系控制系四、知识结构图第二章 控制系统的数学模型一、学习要点1.数学模型的数学表达式形式(1)物理系统的微分方程描述;(2)数学工具—拉氏变换及反变换; (3)传递函数及典型环节的传递函数;(4)脉冲响应函数及应用。
2.数学模型的图形表示(1)结构图及其等效变换,梅逊公式的应用;(2)信号流图及梅逊公式的应用。
二、基本要求1、正确理解数学模型的特点,对系统的相似性、简化性、动态模型、静态模型、输入变 量、输出变量、中间变量等概念,要准确掌握。
2、了解动态微分方程建立的一般方法及小偏差线性化的方法。
3、掌握运用拉氏变换解微分方程的方法,并对解的结构、运动模态与特征根的关系、零输入 响应、零状态响应等概念有清楚的理解。
5-6 开环对数频率特性和时域指标
根据系统开环对数频率特性对系统性能的不同影响,将系统开环对数频率特性分为三个频段。
即低频段、中频段和高频段。
一、 低频段
低频段通常是指开环对数幅频特性的渐近曲线在第一个交接频率以前的频段,这一频段完全由开环传递函数中的积分环节和放大环节所决定。
低频段的对数幅频为
ωωωωlg 20lg 20lg 20)()(lg 20⨯-==v K K
j H j G v (5-32)
式中v 为开环传递函数中的积分环节数。
根据式(5-32)及积分环节数,就可作出开环对数幅频特性曲线的低频段,如图5-39所示。
若已知低频段的开环对数幅频特性曲线,则很容易得到K 值和积分环节数v ,故低频段的频率特性决定了系统的稳态性能。
二、中频段
中频段是指开环对数幅频特性曲线截止频率c ω附近的频段。
这决定系统的稳定程度,即决定系统的动态性能。
设有二个系统,均为最小相位系统,它们的开环对数幅频特性曲线除中频段的斜率不同(即一个为20-dB/dec,另一个为40-dB/dec) 之外, 其余低频、 高频段均相同。
并且中频段相当长,如图5-40 所示。
显然,系统(a)有将近90°的相裕量,而系统(b)则相裕量很小。
假定另有二个系统, 均为最小相位系统, 开环对数幅频特性曲线除中频段 (斜率为 -20 dB/dec ) 线段的长度不同外, 其余部分完全相同, 如图 5-41 所示。
显然, 中频段线段较长的系统 (a) 的相裕量将大于中频段线短的系统(b)。
可见,开环对数幅频特性中频段斜率最好为20-dB/dec ,而且希望其长度尽可能长些,以确保系统有足够的相角裕量。
如果中频段的斜率为40-dB/dec 时,中频段占据的频率范围不宜过长,否则相裕量会很小;若中频段斜率更小(如60-dB/dec),系统就难以稳定。
另外,截止频率c ω越高,系统复现信号能力越强,系统快速性也就越好。
三、 高频段
高频段是指开环对数幅频特性曲线在中频段以后的频段(一般c ωω10>的频段)。
这部分特性是由系统中时间常数很小的部件所决定。
由于它远离截止频率c ω,一般幅值分贝数较低,故对系统动态性能(相裕量)影响不大。
另外,由于高频段的开环幅值较小,故对单位反馈系统有
()()
1()G j j G j ωΦωω=
+
)(ωj G ≈
该式表明,闭环幅值近似等于开环幅
值。
因此,系统开环对数幅频特性在高频段
的幅值,直接反映了系统对输入端高频干扰
的抑制能力。
所以,高频段的分贝数值愈低,系统的抗干扰能力愈强。
图5-42为典型的一型高阶系统开环对数幅频特性曲线的三个频段的划分。
应当指出,三个频段的划分并没有严格的确定准则,但是三个频段的概念为直接运用开
环频率特性来判别、估算系统性能指出了方向。
四、 从相裕量γ估算时域指标
相裕量γ是在频域内描述系统稳定程度的指标,而系统的稳定程度直接影响时域指标%σ和s t ,因此,γ必定与%σ和s t 存在内在联系。
1、 二阶系统的时域指标 二阶系统的相裕量与时域指标间有确定的关系。
分析图5-43所示二阶系统,其开环传递函数
)
2()(2n n s s s G ξωω+= )121
(2+=
s s n n ξωξω
其开环对数幅频特性曲线如图5-44所示。
二阶系统的结构参量ξ、n ω,在时域分析中已建立了与时域指标间的关系式,即
%100%21/⨯=--ξξπσe
n s t ξω5.3=
21ξωπ
-=n p t
式中自然频率n ω可从渐近对数幅频曲线上确定。
在图5-44中,斜率为40-dB/dec 的线段(或其延
长线)与零分贝的交点即为n ω。
因为该点频率恰好
是ξ2n ω和n ω/ξ2频率的几何平均值。
下面求解γ与ξ的关系式:
根据相裕量的定义
式,即
c c c j G ξωωωγ2arctan 90)(180-︒=∠+︒= (5-33)
当开环幅频等于1。
即()1c G j ω=,得
24241ξξωω-+=n
c
将上式代入(5-33)式,得 242412arctan ξξξ
γ-+= (5-34)
根据式(5-34)绘制ξγ-曲线,如图5-45所示。
由图可见,γ越大,ξ也越大;γ越小,ξ就越小。
要想得到满意的动态过程,一般γ取值范围在︒︒70~30之间。
由开环对数幅频特性求时域指标的方法:首先从开环对数幅频特性曲线上求得n ω和γ值,然后根据γ值查图5-45获得ξ值,最后由ξ值查图3-14便可得到%σ;将n ω、ξ值代入式(3-16)和(3-18)分别求得p t 和s t 。
2
对于高阶系统,γ毕竟只是比较简单的一项指标,它不能
完全概括千变万化的频率特性形状。
γ相同的系统,频率特性
未必完全相同,因此时域指标也不会一样。
所以在高阶系统中,
γ与时域指标之间没有确定的函数关系。
但是,通过对大量系
统的研究。
可归纳出下面两个近似的计算公式 ,1sin 14.016.0⎪⎪⎭⎫
⎝⎛-+=γσp ︒≤≤︒9035γ
(5-35)
⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-+=21sin 15.21sin 15.12γγωπc s t
(5-36)
根据以上公式绘制成曲线如图5-46所示。
应当指出,根据计算公式或查图5-46所得结果,当γ较小时,比较接近实际系统,即准确度就高;而当γ较大时,近似程度较差,准确度就低。