对数频率特性如下图所示
- 格式：ppt
- 大小：295.00 KB
- 文档页数：11
下载文档原格式
合集下载
机电控制四次网上作业汇总
选择题（共 10 道试题，共30分。
）峰值h(t p)超出终值h(∞)的百分比叫超调量。
已知系统闭环传递函数为：φ(s)=1/0.25s2+0.707s+1则系统的ts（5％）是（或者则系统的ωn为2）(或者：则系统的超调σ％为0.043)（或者：则系统的阻尼比ξ为0.707）阶跃响应从终值的10％上升到终值的90％所需的时间叫上升时间。
在欠阻尼的情况下，二阶系统的单位阶跃响应为振幅按指数规律衰减的简谐振荡6. 阶跃响应到达并保持在终值h(∞)+ -5%误差带内所需的最短时间；有时也用终值的+ -2％误差带来定义叫调节时间。
阶跃响应第一次达到终值h(∞)的50％所需的时间叫延迟时间。
一阶微分环节波德图渐近线斜率为20dB/dec二阶系统的临界阻尼比是 1 ？以下属于一阶系统的阶跃响应特点的是没有超调量？下列开环传递函数所表示的系统，属于最小相位系统的有s+2/(s+3)(s+2)下列开环传递函数所表示的系统，属于最小相位系统的是s+1/(2s+1)(3s+1)劳斯稳定判据能判断什么系统的稳定性？线性定常系统20db/dec,通过ω=1点的直线。
单位阶跃函数的拉普拉斯变换结果是( 1/S )。
单位斜坡函数的拉氏变换结果是(1/S2)。
以下控制系统按结构分类正确的是开环控制系统、闭环控制系统和复合控制系统阶跃响应越过稳态值h(∞)达到第一个峰值所需的时间叫峰值时间。
某二阶系统的特征根为两个互不相等的实数，则该系统的单位阶跃响应曲线有什么特点？单调上升当时间t满足什么条件时（系统的时间常数为T），一阶系统的阶跃响应值与稳态值之间的误差为5%～2%。
3T< t<4T临界阻尼条件下二阶系统的输出为单调上升曲线。
阶跃响应到达并保持在终值％误差带内所需的最短时间；有时也用终值的％误差带来定义叫调节时间。
当时间t满足什么条件时（系统的时间常数为T），一阶系统的阶跃响应值与稳态值之间的误差为5%～2%。
自动控制原理 第五章第四节对数频率特性(上)
⑹ 振荡环节
G ( j )
=
1−
2 n2
1 + j2
n
L() = −20lg [1 − 2 ]2 + [2 ]2
2 n
n
( ) =
−
arctan
2
n
1
-2Βιβλιοθήκη 2 n−360
+
arctan 2
n
1
-
2
2 n
1
L( ) 0
n
( ) 0 − 3 6 0
1
n
L() −40lg( n )
( ) −180
5.4 对数频率特性(Bode图)（上）
⑺ 二阶复合微分
G ( j )
=
1−
2
2 n
+
j2
n
L( ) = 20lg
[1
−
2
2 n
]2
+
[2
n
]2
( ) =
2
arctan
n 2
1
-
2 n
2
360 − arctan
n 2
1
-
2 n
5.4 对数频率特性(Bode图)（上） ⑻ 延迟环节 G(j ) = e−j
G(j) = j
L( ) = 20 lg ( ) = 90
G(j) = 1 j
L( ) = −20lg ( ) = −90
5.4 对数频率特性(Bode图)（上）
⑷ 惯性环节
G(j) = 1 +1 + jT
L( ) = −20lg 1 + 2T2
− arctanT
( ) = − 180 + arctan T
自动控制原理 题库第六章 线性系统校正 习题
6-1证明RC 无源超前校正环节 最大超前相角为采用半对数坐标时最大超前相角所对应的频率位于两个转折频率的中间或等于零、极点乘积的平方根，即 6-2某单位反馈控制系统的设计指标为上升时间0.1r t ≤秒，超调量%16%σ≤，斜坡输入下的稳态误差0.05ssv e ≤。
（a ）试问系统开环频率特性的低频段需要满足什么要求？中频段需要满足什么要求？（b ）在s 平面内绘制出能满足设计要求的系统主导极点所在的区域。
6-3某系统框图如下图所示，误差c r e -=，01≥K ，02≥K 。
（a ）要求系统对单位斜坡输入t t r =)(的稳态误差3.0≤，主导极点的阻尼比707.0≥ξ，调节时间 2.33s t ≤秒（按5%误差考虑），请在s 平面上绘制出满足上述设计要求的闭环极点的可行区域，给出1K 、2K 应满足的条件。
（b ）设11=K 、2、10，绘制三种情况下以2K 为可变参数的根轨迹。
（c ）设101=K ，确定满足（a ）中性能指标的2K 的值。
6-4下图所示为钟摆的角度控制系统，其中被控对象为阻尼为零的二阶系统。
（a ）试问控制器()c G s 必须满足什么条件，才能使系统为非条件稳定系统？（b ）选用常规调节器，使得系统对阶跃扰动输入w 稳态误差为零，系统还可以做到非条件稳定吗？（c ）选用PID 控制器应用根轨迹方法分析p k 、i T 和d k 发生变化时对系统快速性、稳定性的影响。
答案：应用关系12d i TT k T =和12p i TT k T +=容易给出分析结果。
6-5力、转矩的积分为速度、转速，速度、转速的积分为位置、转角，许多重要的运动控制系统的被控对象可以描述为二重积分器传递函数，即用根轨迹法分析比例控制p k 、比例微分控制(1)p d k k s k s +=+和超前校正(1)(12)k s s ++、(1)(9)k s s ++、(1)(4)k s s ++几种情况下闭环根轨迹的情况和闭环系统的性能。
2第二节对数频率特性
第二节 对数频率特性
1-Apr-21
1
一、对数频率特性曲线（波德图，Bode图）
Bode图由对数幅频特性和对数相频特性两条曲线组成。 ⒈波德图坐标(横坐标是频率，纵坐标是幅值和相角)的分度：
横坐标(称为频率轴)分度：它是以频率w 的对数值 logw 进行 线性分度的。但为了便于观察仍标以w 的值，因此对w 而言是 非线性刻度。w 每变化十倍，横坐标变化一个单位长度，称为 十倍频程(或十倍频)，用dec表示。类似地，频率w 的数值变化
w L(w )
2 20 log
A(w )
20 log
K
w
40
K 10
20log K 20log w,
20
w 当K 1时，w 1, L(w) 0;
20 40
j (w)
1 10 100 K 1 w
当w 10时，L(w) 20 可见斜率为－20/dec 当K 1时，w 1, L(w) 20log K;
0.3
-120° 0.5
-150° 0.7
1.0
-180°
1
1
10T 5T
1
1
2
2T
T
T
对数幅频特性和对数相频特性
图。上图是不同阻尼系数情况
下的对数幅频特性实际曲线与
渐近线之间的误差曲线。
5 T
10 T
当0.3<<0.8，误差约为±4.5dB
1-Apr-21
16
振荡环节的波德图
相频特性：j
1-Apr-21
6
比例环节的bode图
二、典型环节的波德图 ⒈ 比例环节： G(s) K ;
G( jw) K
幅频特性：A(w) K；相频特性：j(w) 0
1-Apr-21
1
一、对数频率特性曲线（波德图，Bode图）
Bode图由对数幅频特性和对数相频特性两条曲线组成。 ⒈波德图坐标(横坐标是频率，纵坐标是幅值和相角)的分度：
横坐标(称为频率轴)分度：它是以频率w 的对数值 logw 进行 线性分度的。但为了便于观察仍标以w 的值，因此对w 而言是 非线性刻度。w 每变化十倍，横坐标变化一个单位长度，称为 十倍频程(或十倍频)，用dec表示。类似地，频率w 的数值变化
w L(w )
2 20 log
A(w )
20 log
K
w
40
K 10
20log K 20log w,
20
w 当K 1时，w 1, L(w) 0;
20 40
j (w)
1 10 100 K 1 w
当w 10时，L(w) 20 可见斜率为－20/dec 当K 1时，w 1, L(w) 20log K;
0.3
-120° 0.5
-150° 0.7
1.0
-180°
1
1
10T 5T
1
1
2
2T
T
T
对数幅频特性和对数相频特性
图。上图是不同阻尼系数情况
下的对数幅频特性实际曲线与
渐近线之间的误差曲线。
5 T
10 T
当0.3<<0.8，误差约为±4.5dB
1-Apr-21
16
振荡环节的波德图
相频特性：j
1-Apr-21
6
比例环节的bode图
二、典型环节的波德图 ⒈ 比例环节： G(s) K ;
G( jw) K
幅频特性：A(w) K；相频特性：j(w) 0
自动控制原理第五章习题及答案
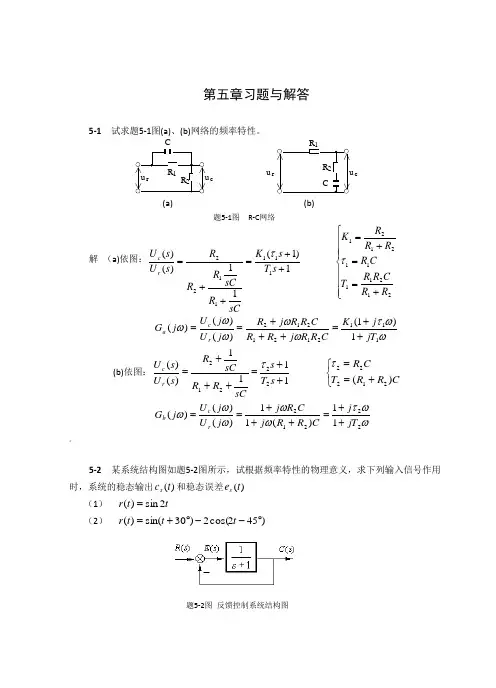
第五章习题与解答5-1试求题5-1图(a)、(b)网络的频率特性。
u r R1u cR2CR2R1u r u c(a) (b)题5-1图R-C网络解（a)依图：⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(RRCRRTCRRRRKsTsKsCRsCRRRsUsUrcττωωτωωωωω11121212121)1()()()(jTjKCRRjRRCRRjRjUjUjGrca++=+++==(b)依图：⎩⎨⎧+==++=+++=CRRTCRsTssCRRsCRsUsUrc)(1111)()(2122222212ττωωτωωωωω2221211)(11)()()(jTjCRRjCRjjUjUjGrcb++=+++=="5-2某系统结构图如题5-2图所示，试根据频率特性的物理意义，求下列输入信号作用时，系统的稳态输出)(tcs和稳态误差)(tes（1）tt r2sin)(=（2）)452cos(2)30sin()(︒--︒+=ttt r题5-2图反馈控制系统结构图解 系统闭环传递函数为: 21)(+=Φs s 频率特性:2244221)(ωωωωω+-++=+=Φj j j 幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-=-系统误差传递函数: ,21)(11)(++=+=Φs s s G s e则 )2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e（1）当t t r 2sin )(=时,2=ω，r m =1则 ,35.081)(2==Φ=ωωj 45)22arctan()2(-=-=j ϕ4.1862arctan )2(,79.085)(2====Φ=j j e e ϕωω )452sin(35.0)2sin()2(-=-Φ=t t j r c m ss ϕ)4.182sin(79.0)2sin()2(+=-Φ=t t j r e e e m ss ϕ （2） 当 )452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωω5.26)21arctan()1(45.055)1(-=-===Φj j ϕ 4.18)31arctan()1(63.0510)1(====Φj j e e ϕ>)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t c m m ss ϕϕ+-⋅Φ-++⋅Φ=)902cos(7.0)4.3sin(4.0--+=t t)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t e e e m e e m ss ϕϕ+-⋅Φ-++⋅Φ=)6.262cos(58.1)4.48sin(63.0--+=t t5-3 若系统单位阶跃响应 h t e e t tt()..=-+≥--11808049试求系统频率特性。
频率响应法示例之二_对数频率特性
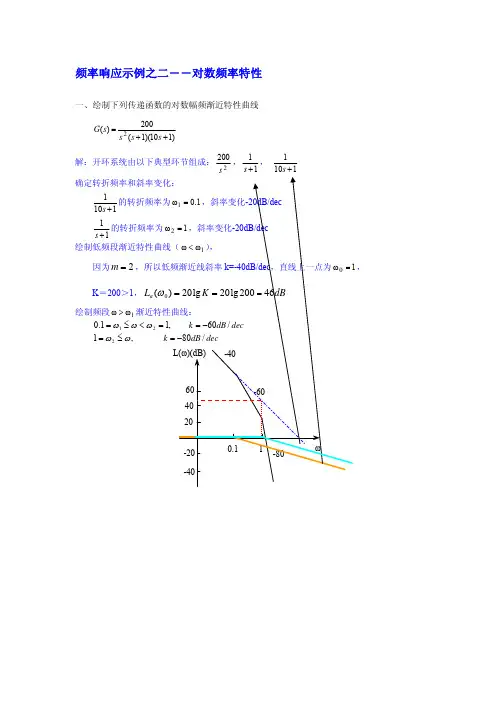
频率响应示例之二――对数频率特性一、绘制下列传递函数的对数幅频渐近特性曲线)110)(1(200)(2++=s s s s G 解：开环系统由以下典型环节组成：2200，11+s ， 1101+s 1101+s 的转折频率为ω11+s 的转折频率为ω2因为2=m ，K ＝200＞1，L a )(0ω绘制频段1ωω> k ,1,11.0221=≤==<≤=ωωωωω2003年4．（10分/150分）已知单位反馈系统的开环传递函数为)164)(12()1.0(16)(22+++++=s s s s s s s G ，试绘制对数幅频特性渐近线 解： dBk s s s s s s s s s s s s s G n n 201.0lg 20lg 2011,4,1,1.0)116416)(12()110(1.0)164)(12()1.0(16)(323212222−========+++++=+++++=时，转折频率为：ωζζωωω2000年4．（10分/70分）系统的对数幅频特性如图所示，据此写出该系统相应的传递函数。
解：图中兰色是解题时作的辅助线及环节示意将对数幅频特性曲线进行分解，从左依次向右可得到系统所包含的开环环节为： K ，111+s T ，12+s T ，113+s T ；其中：2.011=T ；112=T ；1013=T 故：51=T ；12=T ；1.03=T ；又因 20lgK ＝20，故K ＝10所以，系统的传递函数：)11.0)(15()1(10)(+++=s s s s Gw （1/sec ） db 20lg|G|1996年三、2．（10分/60分）系统的对数幅值曲线如图所示。
试推导：系统的传递函数。
解：图中兰色是解题时作的辅助线及环节示意将对数幅频特性曲线进行分解，从左依次向右可得到如图辅助所示的环节⋅sT 11⋅+12s T ⋅+13s T ⋅+114s T ⋅+115s T 116+s T 其中：811=T ；212=T ；413=T ；814=T ；2415=T ；3616=T 故：125.01=T ；5.02=T ；25.03=T ；125.04=T ；04.05=T ；03.06=T 所以，系统的传递函数：)103.0)(104.0)(1125.0()125.0)(15.0(8)(+++++=s s s s s s s G由已知的Bode 图求对象的传递函数小结：1． 根据给出的渐近线，先找出基本的环节与各转折频率――求出时间常数，若有二阶环节，还需要求出ζ值。
机械控制工程基础4习题解答
频特性和相频特性。 分析与提示：首先由系统的输入输出得到系统传递函数；令 s= j 即可得到频率特性， 进而得到幅频特性和相频特性。 答案：由已知条件有
X
i
s
1 s
,
X
o
s
1 s
1 .8
1 s4
0 .8
1 s9
传递函数为
G s X
s X i s
G j
由一个比例环节（比例系数为 K=7.5 ） 、一个积分环节、一个二阶震荡环节（转折频率
1
2s
1
，
2 4
） 、 一个一阶惯性环节 （转折频率 2 2 s 1 ） 、 一个一阶微分环节 （转
1 折频率 3 3 s ）
（1）在横轴上标出 1 , 2 , 3 。 （2） 找出横坐标 1 ， 纵坐标为 20 lg 7 . 5 17 . 5 dB 的点， 过该点作斜率为-20dB/dec 的直线。 （ 3 ） 在 1
ω
dB
】
ω
ωT
0
1 T
-20dB/dec
题目：某环节频率特性 Nyquist 图如图所示，则该环节是【 A．比例环节 B．微分环节 C．积分环节 D．惯性环节 答案： C 题目：频率特性 Nyquist 图为单位圆，则该环节是【 A．比例环节 C．积分环节 答案： D B．微分环节 D．延时环节 】
0 Re
ω
ω
答案： B 题目：单位负反馈系统的开环传递函数为 G ( s ) 答案：系统频率特性为：
G ( jw ) 1 ( jw )( 0 . 1 jw 1) 0 .1 0 . 01
2
1 s (1 0 . 1 s )
对数频率特性
得到
dgω d 1 T2ω2 2 2ζ Tω 2 0 dω dω
ωr
1 T
1 2ζ2 ωn
1 2ζ2
0 ζ 1
2
式中
ωn
1 T
15
将 ωr ωn
1 2ζ2
代入
d2gω
dω2
，不难求得
d2gω
dω2
0
。
因此，在ω=ωr处 gω具 有最小值，亦即 Gjω 此刻具
有最大值。将 ωr ωn 1 2ζ2 代入幅频特性 Gjωr 中，
10
20
()
90o
0o
0.1
1
10
4
4。惯性环节 惯性环节的幅频特性为
Gjω 1
1 jω T
惯性环节的幅频特性
20lg 1 20lg 1 20lg 1 2T 2
1 jT
1 2T 2
在 ω 1 时（低频段）： T 20lg 1 ω2T2 20lg1 0 dB 近似地认为，惯性环节在低频段的对数幅频特性
振荡环节的对数幅频特性在转折频率
ω
n
1 T
附近产生谐振峰值 Gjωr 可通过下列计算得到：
14
振荡环节的幅频 特性为
其中 ：
G jω
1
1
1 T 2ω 2 2 2ζ Tω 2
gω
gω 1 T2ω2 2 2ζ Tω 2
当出现揩振峰值时，Gjω 有最大值，即 gω 有最小值。
无穷时，ω 趋于-90°。 采用渐近线在幅频曲线上产生的误差是可以计算
的。幅值的最大误差发生在转折频率 ω 1 处，近似等 T
于3dB。
20lg 1 1 10lg2 3.01dB
分析表明：惯性环节具有低通特性，对低频输入能 精确地复现，而对高频输入要衰减，且产生相位迟后。 因此，它只能复现定常或缓慢变化的信号。
(整理)自动控制原理试题
试题三一、填空题（每空 1 分，共20分）1、对自动控制系统的基本要求可以概括为三个方面，即： 、快速性和 。
2、控制系统的 称为传递函数。
一阶系统传函标准形式是 ，二阶系统传函标准形式是 。
3、在经典控制理论中，可采用 、根轨迹法或 等方法判断线性控制系统稳定性。
4、控制系统的数学模型，取决于系统 和 , 与外作用及初始条件无关。
5、线性系统的对数幅频特性，纵坐标取值为 ，横坐标为 。
6、奈奎斯特稳定判据中，Z = P - R ，其中P 是指 ，Z 是指 ，R 指 。
7、在二阶系统的单位阶跃响应图中，s t 定义为 。
%σ是 。
8、PI 控制规律的时域表达式是 。
P I D 控制规律的传递函数表达式是 。
9、设系统的开环传递函数为12(1)(1)Ks T s T s ++，则其开环幅频特性为 ，相频特性为 。
二、判断选择题(每题2分，共 16分)1、关于线性系统稳态误差，正确的说法是：( )A 、 一型系统在跟踪斜坡输入信号时无误差 ；B 、 稳态误差计算的通用公式是20()lim 1()()ss s s R s e G s H s →=+；C 、 增大系统开环增益K 可以减小稳态误差；D 、 增加积分环节可以消除稳态误差，而且不会影响系统稳定性。
2、适合应用传递函数描述的系统是 ( )。
A 、单输入，单输出的线性定常系统；B 、单输入，单输出的线性时变系统；C 、单输入，单输出的定常系统；D 、非线性系统。
3、若某负反馈控制系统的开环传递函数为5(1)s s +，则该系统的闭环特征方程为 ( )。
A 、(1)0s s +=B 、 (1)50s s ++=C 、(1)10s s ++=D 、与是否为单位反馈系统有关4、非单位负反馈系统，其前向通道传递函数为G(S)，反馈通道传递函数为H(S)，当输入信号为R(S)，则从输入端定义的误差E(S)为 ( )A 、 ()()()E S R S G S =⋅B 、()()()()E S R S G S H S =⋅⋅C 、()()()()E S R S G S H S =⋅-D 、()()()()E S R S G S H S =- 5、已知下列负反馈系统的开环传递函数，应画零度根轨迹的是 ( )。
自动控制原理5第二节对数频率特性
19
② 一阶微分： A(w) 1 T 2w2，(w) tg1Tw
一阶微分环节的波德图
L(w) 20lg 1 T 2w2 对数幅频特性（用渐近线近似）：
低频段渐近线：当Tw 1时，A(w) 1， 20 log A(w) 0 高频段渐近线：当Tw 1时，A(w) Tw，L(w) 20 log Tw
第二节 对数频率特性
1
一、对数频率特性曲线（波德图，Bode图）
Bode图由对数幅频特性和对数相频特性两条曲线组成。 ⒈波德图坐标(横坐标是频率，纵坐标是幅值和相角)的分度：
横坐标(称为频率轴)分度：它是以频率w 的对数值 logw 进行 线性分度的。但为了便于观察仍标以w 的值，因此对w 而言是 非线性刻度。w 每变化十倍，横坐标变化一个单位长度，称为 十倍频程(或十倍频)，用dec表示。类似地，频率w 的数值变化
来计算只能求出±90°之间的值(tg-1函数的主值范围)，也就是
说当 w ( 1 , ) 时，用计算器计算的结果要经过转换才能得到 。 即当 w (T1 , ) 时，用计算器计算的结果要减180°才能得到 。
T
或用下式计算
(w) tg1 Tw 1 2 tg1 Tw 1 2
17
微分环节的频率特性
(w) K
0 180
K 0 K 0
180
7
K 0
⒉ 积分环节的频率特性：G(s) K
s
频率特性：
G( jw )
K
j
K
K
e2
jw w w
积分环节的Bode图
L(w) / dB
40 20w ) tg1( K 0)
w
2
L(w) 20log A(w) 20log K
自动控制系统的频域分析法
n 2 n2
当 n 时：L() 20lg | G( j) | 20lg1 0 dB
() 00
当 n 时：L() 20 lg | G( j) | 10 lg( )41 40lg( )
nnBiblioteka () 180 0当 n 时：L() 20lg | G( j) | 20lg(2 )
2k
k
1 2
k2
从上式可以看出，系统中包含了如下几个典型环节：
① 比例环节 K
；② 积分环节
1
j
；③一阶微分
环节 j 1 ；④惯性环节 1
1
jT 1
和⑤振
荡环节 (1 ( )2 2 )
n
n
对于上述这些典型环节的概略对数频率特性曲线我们
很清楚，因此，无论是对数幅频特性还是对数相频特性均
可以用这些基本环节组合而成。这就是一般系统频率特性
极坐标平面如下图所示：
对数频率特性图
对数频率特性图又称为伯德图，它由对数幅频曲线和对数 相频曲线组成，是工程中广泛使用的一种分析工具。现将 频率特性表示如下：
G( j) | G( j) | e j()
对数幅频特性曲线的横坐标按 lg 分度，单位为弧度/秒
(rad s) ，其纵坐标按 L() 的线性分度，单位是分贝 (dB) 。 其中L() 的表达式如下：
开环传递函数中零点位于原点处的因子称为微分环节
频率特性： G( j) j
对数幅频特性为：20lg | j | 20lg dB
对数相频特性为：() 90 0
其幅相曲线图和对数频率特性图分别如下图所示：
一阶微分环节（Ts 1, T 0 ）
频率特性：G( j) jT 1 对数幅频特性： L() 20 lg | G( j) | 10 lg(1 (T)2 )
对数频率特性讲解
在右半s平面内既无极点也无零点的传递函数 非最小相位传递函数
在右半s平面内有极点和（或）零点的传递函数 最小相位系统
具有最小相位传递函数的系统 非最小相位系统
具有非最小相位传递函数的系统
请看例子
1 jT G1( j) 1 jT1
jω
G2
(
j)
1 1
jT jT1
,
jω
0 T T1
0 2 0.707
2
谐振峰值
(5-25)
当 0.707 时，幅值曲线不可能有峰值出现，即不会有谐振
请看 M r 与 关系曲线
15
10
M r /dB
5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
图: M r 与 关系曲线
开环系统的伯德图 步骤如下
写出开环频率特性表达式，将所含各因子的转折频率由 大到小依次标在频率轴上
0.1
0.2 0.3
0.5 0.7
1.0
-140
-160
-180
10-1
100
101
图: 二阶因子的对数相频特性曲线
谐振频率谐振峰值
d g() 2(1 2 )(2 ) 2(2 )2 1 0
dt
n2
n2
n n
g ( )
1 . 比例环节K
L() 20log K
() 0
21
20.5
Bode Diagram of G(jw )=K=10
Magnitude (dB)
20
19.5
19 1
在右半s平面内有极点和（或）零点的传递函数 最小相位系统
具有最小相位传递函数的系统 非最小相位系统
具有非最小相位传递函数的系统
请看例子
1 jT G1( j) 1 jT1
jω
G2
(
j)
1 1
jT jT1
,
jω
0 T T1
0 2 0.707
2
谐振峰值
(5-25)
当 0.707 时，幅值曲线不可能有峰值出现，即不会有谐振
请看 M r 与 关系曲线
15
10
M r /dB
5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
图: M r 与 关系曲线
开环系统的伯德图 步骤如下
写出开环频率特性表达式，将所含各因子的转折频率由 大到小依次标在频率轴上
0.1
0.2 0.3
0.5 0.7
1.0
-140
-160
-180
10-1
100
101
图: 二阶因子的对数相频特性曲线
谐振频率谐振峰值
d g() 2(1 2 )(2 ) 2(2 )2 1 0
dt
n2
n2
n n
g ( )
1 . 比例环节K
L() 20log K
() 0
21
20.5
Bode Diagram of G(jw )=K=10
Magnitude (dB)
20
19.5
19 1
对数 频率特性
相频特性曲线的纵坐标以度或弧度为单位进行线性分度。
一般将幅频特性和相频特性画在一张图上，使用同一个横 坐标（频率轴）。
当幅制特性值用分贝值表示时，通常将它称为增益。幅值 和增益的关系为：增益 20 log(幅值)
幅值A()
1.0 0
1.2 6
1.5 6
2.0 0
2.5 1
3.1 6
5.6 2
10. 0
Dec Dec Dec Dec
log
... 2 1 0 1 2
0
0.01 0.1
1
10 100
由于 以对数分度，所以零频率线在－∞处。
Thursday, September
10, 2020
2
更详细的刻度如下图所示
1
2
3 4 5 6 7 8 910
20
一倍频程 一倍频程 一倍频程
一倍频程
30 40 50 60 80 100 一倍频程
十倍频程 十倍频程
十倍频程
一倍频程 十倍频程
lg
0
1
2
ω １ 2 3 4 5 6 7 8 9 10
lgω
0.00 0
0.30 1
0.47 7
0.60 2
0.69 9
0.77 8
0.84 5
0.90 3
0.95 4
1.00 0
Thursday, September
10, 2020
3
纵坐标分度：对数幅频特性曲线的纵坐标以 L() 20log A() 表 示。其单位为分贝(dB)。直接将 20log A()值标注在纵坐标上。
第三节 对数频率特性
Thursday, September
10, 2020
一般将幅频特性和相频特性画在一张图上，使用同一个横 坐标（频率轴）。
当幅制特性值用分贝值表示时，通常将它称为增益。幅值 和增益的关系为：增益 20 log(幅值)
幅值A()
1.0 0
1.2 6
1.5 6
2.0 0
2.5 1
3.1 6
5.6 2
10. 0
Dec Dec Dec Dec
log
... 2 1 0 1 2
0
0.01 0.1
1
10 100
由于 以对数分度，所以零频率线在－∞处。
Thursday, September
10, 2020
2
更详细的刻度如下图所示
1
2
3 4 5 6 7 8 910
20
一倍频程 一倍频程 一倍频程
一倍频程
30 40 50 60 80 100 一倍频程
十倍频程 十倍频程
十倍频程
一倍频程 十倍频程
lg
0
1
2
ω １ 2 3 4 5 6 7 8 9 10
lgω
0.00 0
0.30 1
0.47 7
0.60 2
0.69 9
0.77 8
0.84 5
0.90 3
0.95 4
1.00 0
Thursday, September
10, 2020
3
纵坐标分度：对数幅频特性曲线的纵坐标以 L() 20log A() 表 示。其单位为分贝(dB)。直接将 20log A()值标注在纵坐标上。
第三节 对数频率特性
Thursday, September
10, 2020
作业答案 某最小相位系统的开环对数幅频特性如图所示要求：1 写出
式中G(s)=num/den,频率ω自动选择范围从 ω=0.1到ω=1000rad/sec ❖若人为选择频率范围,可应用logspace函数 调用格式：ω=logspace(a,b,n) ❖采用自动频率范围,上述MATLAB命令可简化
bode(num,den)
Nyquist图
❖调用格式 ［re,im,ω］=nyquist(num,den,ω) 式中G(s)=num/den；ω用户提供的频率 范围；re极坐标的实部；im极坐标的虚部
❖若用户不指定频率ω范围，则为 Nyquist(num,den)
❖在MATLAB中可采用裕量函数margin( )来 求取相对稳定性，其调用格式为
［Kg,, ωg, ωc］＝margin(mag,phase,ω） Kg-------- 增益裕量; -------- 相角裕量; ωg --------穿越-180°线所对应的频率; ωc --------幅值为0dB时所对应的频率
Gc (s)
(1 0.25s)(1 0.12s) (11.33s)(1 0.022 s)
4）校正后系统开环传递函数：
G(s)
70(1 0.25s)
s(11.33s)(1 0.02s)(1 0.022 s)
直接计算，得：ωc =13，γ=45.6,Mr=1.4, p
%=32%,ts=0.73 满足设计要求。
1
(T1 1
T2 T2 s
)s
图6-4有源超前校正装置
K
p
1
T1s 1 T2s
式中：Kp=Rf/R1,T1=R1C,, T2=R2C
实际PID控制器的传递函数：
Gc (s)
K
p
1
1 Ti s
bode(num,den)
Nyquist图
❖调用格式 ［re,im,ω］=nyquist(num,den,ω) 式中G(s)=num/den；ω用户提供的频率 范围；re极坐标的实部；im极坐标的虚部
❖若用户不指定频率ω范围，则为 Nyquist(num,den)
❖在MATLAB中可采用裕量函数margin( )来 求取相对稳定性，其调用格式为
［Kg,, ωg, ωc］＝margin(mag,phase,ω） Kg-------- 增益裕量; -------- 相角裕量; ωg --------穿越-180°线所对应的频率; ωc --------幅值为0dB时所对应的频率
Gc (s)
(1 0.25s)(1 0.12s) (11.33s)(1 0.022 s)
4）校正后系统开环传递函数：
G(s)
70(1 0.25s)
s(11.33s)(1 0.02s)(1 0.022 s)
直接计算，得：ωc =13，γ=45.6,Mr=1.4, p
%=32%,ts=0.73 满足设计要求。
1
(T1 1
T2 T2 s
)s
图6-4有源超前校正装置
K
p
1
T1s 1 T2s
式中：Kp=Rf/R1,T1=R1C,, T2=R2C
实际PID控制器的传递函数：
Gc (s)
K
p
1
1 Ti s
《对数频率特性》课件
表示信号在传输过程中产生的相位偏移。
带宽参数则表示系统能够处理的信号频率范围，这些参数对于
03
理解和优化系统性能至关重要。
数学模型的适用范围
01
对数频率特性数学模型适用于 描述和分析各种类型的电子系 统和信号处理系统，如音频处 理、通信、雷达等。
02
该模型尤其适用于分析具有非 线性或非平坦频率响应的系统 ，这些系统在常规的线性频率 坐标系下难以准确描述。
优缺点对比分析
• 对数频率特性的优点主要在于其能够 提供较大的动态范围和接近人耳的感 知特性，使得音频信号的还原更加真 实和平衡。然而，其缺点在于可能会 产生非线性失真，不易于控制，并且 可能不适合所有应用场景。在选择使 用对数频率特性时，需要根据实际需 求进行权衡和考虑。
05 对数频率特性的未来发展
分析该对数频率特性，可以发现系统在低频段增益较高，而 在高频段增益迅速下降，具有良好的低通滤波器特性。
02
03
动态范围大
对数频率特性能够提供较 大的动态范围，使得音频 信号在低频和高频之间的 变化更加平滑。
接近人耳感知
对数频率特性与人耳的感 知特性较为接近，因此能 够更好地还原声音的真实 感。
计算步骤
01
确定系统的频率响应函数$H(f )$。
02 对$H(f)$取对数，得到对数频率特性$L(f)$。
03 分析$L(f)$的特性，如最大值、最小值、转折点 等，以了解系统在不同频率下的性能。
计算实例
假设一个系统的频率响应函数为$H(f) = 10 times frac{1}{10^3 + f^2}$，则其对应的对数频率特性为$L(f) = log(10 times frac{1}{10^3 + f^2})$。
控制工程基础模拟试卷一及答案
《控制工程基础》模拟试卷一一、填空题（20分）1、 1、系统的稳态误差与输入信号的形式及___系统的结构和参数或系统的开环传递函数_有关。
2、对于一个自动控制系统的性能要求可以概括为三个方面：稳定性、 快速 性和___准确___性。
3、传递函数的定义是对于线性定常系统,在____初始条件为零____的条件下，系统输出量的拉氏变换与____输入量的拉氏变换___之比。
4、传递函数的组成与输入、输出信号无关，仅仅决定于___系统本身的结构和参数____，并且只适于零初始条件下的_____线性定常____系统。
5、判别系统稳定性的出发点是系统特征方程的根必须为____负实根或负实部的复数根___，即系统的特征根必须全部在____复平面的左半平面_____是系统稳定的充要条件。
6、频率响应是系统对______正弦输入____稳态响应，频率特性包括____幅频和相频_____两种特性。
2、 7、系统的性能指标按其类型可分为_______时域性能指标，频域性能指标，综合性能指标_______。
3、 8、用频率法研究控制系统时，采用的图示法分为极坐标图示法和____对数坐标____ 图示法。
9、系统稳定的充要条件是：____系统的全部特征根都具有负实部____。
10、对广义系统，按反馈情况可分为____开环系统，闭环系统____ 。
11、I 型系统G s K s s ()()=+2在单位阶跃输入下，稳态误差为__0_，在单位加速度输入下，稳态误差为__∞__。
二、选择题（20分）1、拉氏变换将时间函数变换成 （ D ）A ．正弦函数B ．单位阶跃函数C ．单位脉冲函数D ．复变函数2、微分环节的频率特性相位移θ(ω)= （ A ）A. 90°B. -90°C. 0°D. -180°3、设系统的传递函数为G(s)=255252++s s ，则系统的阻尼比为 （ C ） A.25 B. 5 C. 21 D. 1 4、正弦函数sin t ω的拉氏变换是 （ B ） A.ω+s 1 B.22s ω+ω C.22s s ω+ D. 22s 1ω+ 5、比例环节的频率特性相位移θ(ω)= （ C )A.90°B.-90°C.0°D.-180°6、一阶系统的阶跃响应， ( D )A.当时间常数T较大时有振荡B.当时间常数T较小时有振荡C.有振荡D.无振荡7、系统特征方程式的所有根均在根平面的左半部分是系统稳定的 ( C )A.充分条件B.必要条件C.充分必要条件D.以上都不是8、时域分析法研究自动控制系统时最常用的典型输入信号是（ D ）A．脉冲函数B．斜坡函数C．抛物线函数D．阶跃函数9、令线性定常系统传递函数的分母多项式为零，则可得到系统的 ( B )A．代数方程B．特征方程C．差分方程D．状态方程10、线性定常系统的传递函数，是在零初始条件下（ D ）A．系统输出信号与输入信号之比B．系统输入信号与输出信号之比C．系统输入信号的拉氏变换与输出信号的拉氏变换之比D．系统输出信号的拉氏变换与输入信号的拉氏变换之比三、简答题（20分）1、什么是反馈？为什么要进行反馈控制？答：反馈是指人们为了达到一定的目的，有意加入的反馈，闭环控制系统的工作是基于系统的实际输出与输入间的偏差之上的，在系统存在扰动的情况下，这种偏差就会出现。
[应用]根据最小相位系统开环对数频率特性求对应开环传递函数
![[应用]根据最小相位系统开环对数频率特性求对应开环传递函数](https://img.taocdn.com/s1/m/6cf15ac329ea81c758f5f61fb7360b4c2e3f2add.png)
根据最小相位系统开环对数频率特性求对应的开环传递函数（类似作业第八题），是《自动控制原理》课程的常考题型。
对于此类题目，首先需要理解以下几点：（1） 系统开环传递函数的一般表达式为：()1212m m22i k k k 00i 1k 1K 0n n v v 22j j 11(τs 1)(τs 2ζτs 1)K K G s G (s)s s (Ts 1)(T s 2ζTs 1)l l l l ====+++=⋅=+++∏∏∏∏ 其中∏为连乘符号，为积分环节，是积分环节个数。
i τs 1+代表第个微分环节，j Ts 1+代表第j 个惯性环节，22T s 2ζTs 1l l l ++代表第l 个震荡环节。
作业或考试中，考查的开环传递函数比（2）根据（1）可知，要确定()K G s ，求出、m1、n1、j T 的值。
（3）当开环对数频率特性低频段的斜率分别为0、-20、-40时，对应的分别等于0、1、2。
（教材图5-32）（4）对0型系统：当L(0)=20lgK ；对I 型系统：低频渐近线或其延长线与零分贝线相交的频率；当=1时，L(1)=20lgK ；对II 型系统：低频渐近线或其延长线与零分贝线相交的频率；当=1时，L(1)=20lgK 。
（5）当曲线经过微分环节时，斜率变化；当曲线经过惯性环节时，斜率变化。
（6因此，根据最小相位系统开环对数频率特性求对应的开环传递函数的步骤如下：（1） 由低频段的斜率确定；（2） 由及低频渐近线或其延长线与零分贝线相交的频率确定K ；（3） 根据曲线斜率变化确定微分环节、惯性环节的个数；（4） 由转折频率确定时间常数。
以下题为例，给出详细解答过程。
已知最小相位系统开环对数频率特性(渐近线)如下图所示，（1）写出开环传递函数； （2）根据相角裕度判别系统的稳定性。
解：（1）A .由低频段的斜率为，可知，II 系统；B . 曲线斜率由变到，斜率变化+20，可知经过一个微分环节。
机械工程控制基础计算题
502 •，n 2 • 2 三、设系统的闭环传递函数为 Gc(s)= s 2 '，n ^ ' 'n ，试求最大超调量＜T % =9.6%、峰值时间tp=0.2秒时的闭环传递函数的参数 E 和3 n 的值。
六、某系统如下图所示，试求其无阻尼自然频率3n ，阻尼比Z ，超调量＜7 %，峰值时间t p ，调整时间t s ( △=0.02)。
-ijl 解：T ：「% = e 一 100% =9.6% 二 E =0.6 解：对于上图所示系统，首先应求 出其传递函数，化成标准形式，然后 可用公式求出各项特征量及瞬态响 应指标。
T t p = ' = 0.2 ；：：n :：1 ―_ 314 _19.6rad/st p 1 -Z 2 02.. 1_0.62 ■ ■ 3 n' 314 2 --n四、设一系统的闭环传递函数为 G c (s)= p 牙，试求最大 s +2M0nS +C0n超调量＜r % =5%、调整时间t s =2秋△ =0.05)时的闭环传递函数的参数 E 和3 n 的值。
1—解：% = e _100% =5%/. £ =0.69 3 T t s = — ''n'二 3 n =2.17rad/s五、设单位负反馈系统的开环传递函数为 G k (s)- 25 s(s 6)求(1)系统的阻尼比Z 和无阻尼自然频率 (2)系统的峰值时间 如超调量7%、调整时间t s (A =0.02); 解：系统闭环传递函数 25s(s 6) 100s50s 4100士 ______Xi (s ) 1+100002 s50s +4)+2 s 2+0.08s+0.04q50s+4 J与标准形式对比，可知2 W n = 0.08w ； =0.04n = 0.2 rad= 0.2/st p t s——:——2 : 16.03 s 0.2.1 -0.22“1亠 s(s 6)s(s 6) 25 s 26s 25 4& ----- 沁 n0.2X0.2 100(s ) 八、已知单位负反馈系统的开环传递函数如下:与标准形式对比，可知 ,w ：= 25 W n =5= 0.6 w d = w n . 1 - 2=5 iM -0.62=4G K (S )2S 2(S + 0.1)(S + 0.2)求：(1)试确定系统的型次V 和开环增益K ;2(2)试求输入为r (t^ 5 2t 4t 时，系统的稳态误差。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
特性，并判定系统的稳定性及计算相角裕度γ。
100(1 0.01s ) G K ( s ) ，试绘出系统的对数频率 s (1 0.1s )
解：1、K＝100，ν ＝1，交接频率
ω1，
1 1 。 ω2 10 100 0.1 0.01
2、低频渐近线的斜率为－20νdB/dec=－20dB/dec。 当ω＝1时，L(ω)=20logK＝40dB。即低频渐近线的斜率为－20，且过点(1， 40)。 当ω＝10时，斜率变为－40dB/dec； 当ω＝100时，斜率变为－20dB/dec； 3、高频渐近线的斜率为－20（n-m）dB/dec=－20dB/dec。
显见 N＋＝0，N－＝0。
N ＝ N＋－ N－ ＝ 0 根据 GK(s) 表达式知道，P ＝0。由于 Z ＝P －2 N ＝0
Kπ ts (s) ωc
其中
K 2 1.5(M p 1) 2.5(M p 1) 2
1 M p 1.8
调节时间ts随Mp的增大而增大，且随ωc的增大而减小。 ts和ωc 的反比关系正是频率尺度与时间尺度反比性质的体现。
3、带宽频率ωb和ξ之间的关系
ωb (1 2ξ 2 ) 2 4ξ 2 4ξ 4 ωn
(∞ ) ＝ －180 °，曲线沿负虚轴、以 n - m
-
2
π π
开环传递函数在右半 s 平面上的开环极点数P ＝0
当ω 从0变化到＋∞，奈氏曲线不包围 (－1， 0 )点， R ＝ 0 Z ＝ P － R ＝0－0＝0，故闭环系统稳定。
jQ
100
ω
ω 1 0
P
ω0
P151－5－19（3）:系统的开环传递ω2 100 Q(ω) ω(1 ω 2 )
A(ω) 100 ω 1 ω2
P(ω)
100
幅频特性
φ(ω) 90 tan1 ω
当ω＝ 0时，P(0) ＝－100，Q(0) ＝ ∞ ， A (0) ＝ ∞, (0 ) ＝ －90°， 特性曲线起始于负虚轴，渐近线为P(ω) ＝－100 ；ω ＝ ∞ 时，P (∞ )＝0 , Q (∞ )＝0 ,A (∞) ＝0, 趋于原点。
–奈奎斯特稳定判据是根据开环频率特性曲线围绕(-1, j0) 点的情况（即N等于多少）和开环传递函数在s右半平面的 极点数P来判别对应闭环系统的稳定性的。这种判据能从图 形上直观地看出参数的变化对系统性能的影响，并提示改 善系统性能的信息。
– 考虑到系统内部参数和外界环境的变化对系统稳定性的影响，要求系统 不仅能稳定地工作，而且还需有足够的稳定裕量。稳定裕量通常用相位裕 量和增益裕量来表示。在控制工程中，一般要求系统的相位裕量在30º 60º 范围内，这是十分必要的。
§5-8 系统暂态特性和闭环 频率特性的关系
1、谐振峰值Mp
谐振峰值Mp是闭环系统幅频特性的最大值。 通常，Mp越大，系统单位过渡特性的超调量δ%也 越大。
p n 1 2 2
Mp 1 2 1 2
1 2
% e
100 %,
0.707
2、谐振峰值Mp和调节时间ts的关系
φ(ω) 90 tan1 0.01ω tan1 0.1ω
ω→0时， ； ω→∞ φ(0) 90 时， 。 () 90
对数频率特性如下图所示。
L( )(dB)
40 20
20
40
20
φ(ω)
0
0 1
10
100
90
180
因为ν ＝1，故如图中虚线所示在对数相频特性的低频段曲线上补作0°到－ 90°的虚线，作为对数相频曲线的一部分。当ω＜ωc 时有L（ω）＞0，且在此频率 范围内，φ （ω ）未曾穿越－180 °线。
–只要被测试的线性系统（或部件）是稳定的，就可以用
实验的方法来估计它们的数学模型。这是频率响应法的
一大优点。
P151－5－19（3）:系统的开环传递函数为
100 ，绘出开环幅相曲线并判 GK (s) s ( s 1)
解： GK ( jω)
100 100 100 j jω( jω 1) 1 ω2 ω(1 ω 2 )
•小结
–频率特性是线性系统（或部件）的正弦输入信号作用下的 稳态输出和输入之比。它和传递函数、微分方程一样能反 映系统的动态性能，因而它是线性系统（或部件）的又一 形式的数学模型。
–传递函数的极点和零点均在s平面左方的系统称为最小相位 系统。由于这类系统的幅频特性和相频特性之间有着唯一 的对应关系，因而只要根据它的对数幅频特性曲线就能写 出对应系统的传递函数。
100(1 0.01s ) G K ( s ) ，试绘出系统的对数频率 s (1 0.1s )
解：1、K＝100，ν ＝1，交接频率
ω1，
1 1 。 ω2 10 100 0.1 0.01
2、低频渐近线的斜率为－20νdB/dec=－20dB/dec。 当ω＝1时，L(ω)=20logK＝40dB。即低频渐近线的斜率为－20，且过点(1， 40)。 当ω＝10时，斜率变为－40dB/dec； 当ω＝100时，斜率变为－20dB/dec； 3、高频渐近线的斜率为－20（n-m）dB/dec=－20dB/dec。
显见 N＋＝0，N－＝0。
N ＝ N＋－ N－ ＝ 0 根据 GK(s) 表达式知道，P ＝0。由于 Z ＝P －2 N ＝0
Kπ ts (s) ωc
其中
K 2 1.5(M p 1) 2.5(M p 1) 2
1 M p 1.8
调节时间ts随Mp的增大而增大，且随ωc的增大而减小。 ts和ωc 的反比关系正是频率尺度与时间尺度反比性质的体现。
3、带宽频率ωb和ξ之间的关系
ωb (1 2ξ 2 ) 2 4ξ 2 4ξ 4 ωn
(∞ ) ＝ －180 °，曲线沿负虚轴、以 n - m
-
2
π π
开环传递函数在右半 s 平面上的开环极点数P ＝0
当ω 从0变化到＋∞，奈氏曲线不包围 (－1， 0 )点， R ＝ 0 Z ＝ P － R ＝0－0＝0，故闭环系统稳定。
jQ
100
ω
ω 1 0
P
ω0
P151－5－19（3）:系统的开环传递ω2 100 Q(ω) ω(1 ω 2 )
A(ω) 100 ω 1 ω2
P(ω)
100
幅频特性
φ(ω) 90 tan1 ω
当ω＝ 0时，P(0) ＝－100，Q(0) ＝ ∞ ， A (0) ＝ ∞, (0 ) ＝ －90°， 特性曲线起始于负虚轴，渐近线为P(ω) ＝－100 ；ω ＝ ∞ 时，P (∞ )＝0 , Q (∞ )＝0 ,A (∞) ＝0, 趋于原点。
–奈奎斯特稳定判据是根据开环频率特性曲线围绕(-1, j0) 点的情况（即N等于多少）和开环传递函数在s右半平面的 极点数P来判别对应闭环系统的稳定性的。这种判据能从图 形上直观地看出参数的变化对系统性能的影响，并提示改 善系统性能的信息。
– 考虑到系统内部参数和外界环境的变化对系统稳定性的影响，要求系统 不仅能稳定地工作，而且还需有足够的稳定裕量。稳定裕量通常用相位裕 量和增益裕量来表示。在控制工程中，一般要求系统的相位裕量在30º 60º 范围内，这是十分必要的。
§5-8 系统暂态特性和闭环 频率特性的关系
1、谐振峰值Mp
谐振峰值Mp是闭环系统幅频特性的最大值。 通常，Mp越大，系统单位过渡特性的超调量δ%也 越大。
p n 1 2 2
Mp 1 2 1 2
1 2
% e
100 %,
0.707
2、谐振峰值Mp和调节时间ts的关系
φ(ω) 90 tan1 0.01ω tan1 0.1ω
ω→0时， ； ω→∞ φ(0) 90 时， 。 () 90
对数频率特性如下图所示。
L( )(dB)
40 20
20
40
20
φ(ω)
0
0 1
10
100
90
180
因为ν ＝1，故如图中虚线所示在对数相频特性的低频段曲线上补作0°到－ 90°的虚线，作为对数相频曲线的一部分。当ω＜ωc 时有L（ω）＞0，且在此频率 范围内，φ （ω ）未曾穿越－180 °线。
–只要被测试的线性系统（或部件）是稳定的，就可以用
实验的方法来估计它们的数学模型。这是频率响应法的
一大优点。
P151－5－19（3）:系统的开环传递函数为
100 ，绘出开环幅相曲线并判 GK (s) s ( s 1)
解： GK ( jω)
100 100 100 j jω( jω 1) 1 ω2 ω(1 ω 2 )
•小结
–频率特性是线性系统（或部件）的正弦输入信号作用下的 稳态输出和输入之比。它和传递函数、微分方程一样能反 映系统的动态性能，因而它是线性系统（或部件）的又一 形式的数学模型。
–传递函数的极点和零点均在s平面左方的系统称为最小相位 系统。由于这类系统的幅频特性和相频特性之间有着唯一 的对应关系，因而只要根据它的对数幅频特性曲线就能写 出对应系统的传递函数。