2第二节对数频率特性
- 格式:pps
- 大小:2.83 MB
- 文档页数:42

第二节对数频率特性一、对数频率特性曲线(波德图,Bode 图)Bode 图由对数幅频特性和对数相频特性两条曲线组成。
⒈波德图坐标(横坐标是频率,纵坐标是幅值和相角)的分度:横坐标(称为频率轴)分度:它是以频率w 的对数值log w 进行线性分度的。
但为了便于观察仍标以w 的值,因此对w 而言是非线性刻度。
w 每变化十倍,横坐标变化一个单位长度,称为十倍频程(或十倍频),用dec 表示。
类似地,频率w 的数值变化一倍,横坐标就变化0.301单位长度,称为“倍频程”,用oct 表示。
横坐标的单位是rad /s 。
如下图所示:DecDecDecDec1-2-012...∞-wlog 01.001.0110100w由于w 以对数分度,所以零频率点在-∞处。
12345678910203040506080100一倍频程一倍频程一倍频程一倍频程一倍频程一倍频程十倍频程十倍频程十倍频程十倍频程12wwlg 更详细的刻度如下图所示ω12345678910lg ω0.0000.3010.4770.6020.6990.7780.8450.9030.954 1.000纵坐标分度:对数幅频特性曲线的纵坐标以L(w)=20log A(w) 表示。
其单位为分贝(dB)。
直接将20log A(w) 值标注在纵坐标上。
相频特性j (w)曲线的纵坐标以度或弧度为单位进行线性分度。
一般将幅频特性和相频特性画在一张图上,使用同一个横坐标(频率轴)。
当幅频特性值用分贝值表示时,通常将它称为增益。
幅值和增益的关系为:增益=20log (幅值)幅值A(w ) 1.00 1.26 1.56 2.00 2.51 3.16 5.6210.0100100010000对数幅值02468101520406080 20lg A(w )幅值A(w ) 1.000.790.630.500.390.320.180.100.010.0010.0001对数幅值0-2-4-6-8-10-15-20-40-60-80 20lg A(w )使用对数坐标图的优点:⏹可以展宽频带;频率是以10倍频表示的,因此可以清楚的表示出低频、中频和高频段的幅频和相频特性。

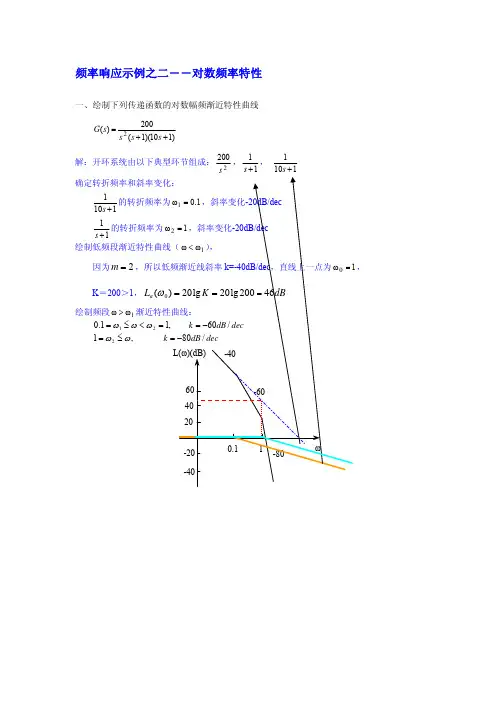
频率响应示例之二――对数频率特性一、绘制下列传递函数的对数幅频渐近特性曲线)110)(1(200)(2++=s s s s G 解:开环系统由以下典型环节组成:2200,11+s , 1101+s 1101+s 的转折频率为ω11+s 的转折频率为ω2因为2=m ,K =200>1,L a )(0ω绘制频段1ωω> k ,1,11.0221=≤==<≤=ωωωωω2003年4.(10分/150分)已知单位反馈系统的开环传递函数为)164)(12()1.0(16)(22+++++=s s s s s s s G ,试绘制对数幅频特性渐近线 解: dBk s s s s s s s s s s s s s G n n 201.0lg 20lg 2011,4,1,1.0)116416)(12()110(1.0)164)(12()1.0(16)(323212222−========+++++=+++++=时,转折频率为:ωζζωωω2000年4.(10分/70分)系统的对数幅频特性如图所示,据此写出该系统相应的传递函数。
解:图中兰色是解题时作的辅助线及环节示意将对数幅频特性曲线进行分解,从左依次向右可得到系统所包含的开环环节为: K ,111+s T ,12+s T ,113+s T ;其中:2.011=T ;112=T ;1013=T 故:51=T ;12=T ;1.03=T ;又因 20lgK =20,故K =10所以,系统的传递函数:)11.0)(15()1(10)(+++=s s s s Gw (1/sec ) db 20lg|G|1996年三、2.(10分/60分)系统的对数幅值曲线如图所示。
试推导:系统的传递函数。
解:图中兰色是解题时作的辅助线及环节示意将对数幅频特性曲线进行分解,从左依次向右可得到如图辅助所示的环节⋅sT 11⋅+12s T ⋅+13s T ⋅+114s T ⋅+115s T 116+s T 其中:811=T ;212=T ;413=T ;814=T ;2415=T ;3616=T 故:125.01=T ;5.02=T ;25.03=T ;125.04=T ;04.05=T ;03.06=T 所以,系统的传递函数:)103.0)(104.0)(1125.0()125.0)(15.0(8)(+++++=s s s s s s s G由已知的Bode 图求对象的传递函数小结:1. 根据给出的渐近线,先找出基本的环节与各转折频率――求出时间常数,若有二阶环节,还需要求出ζ值。