地震子波反褶积程序
- 格式:doc
- 大小:437.00 KB
- 文档页数:19


地震勘探资料处理流程与方法地震勘探资料处理流程与方法提纲引言一、数据加载二、置道头三、静校正四、叠前噪音压制五、振幅补偿六、叠前反褶积七、动校正、切除与叠加八、剩余静校正九、倾角时差校正(DMO) 与叠前时间偏移十、叠后提高分辨率处理十一、叠后噪音压制引言地震勘探分三个阶段。
地震资料采集、地震资料处理、地震资料解释。
其中地震资料处理是连接野外采集和资料解释的关键环节。
所谓地震资料处理,就是利用数字计算机对野外地震助探所获得的原始资料进行加工、改造,以期得到高质量的、可靠的地震信息,为下一步资料解释提供直观的、可靠的依据和有关的地质信息。
野外地震资料中包含着有关地下构造和岩性的信息,包这些信息是叠加在于扰背景上且被些外界因素所扭曲,信息之间往往是互相交织的,不宜直接用于地质解释。
因此,需要对野外采集的地震资料进行室内处理。
常规处理流程,数据输入→置道头→静校正→叠前噪音压制→振幅补偿→叠前反褶积→抽cmp道集→速度分析,动校正、初叠加→剩余静校正→DMo或叠前时间前移→叠后褶积→随机噪音衰减→偏移→时变滤波,增益一、数据加载1、数据输入:将野外磁带数据转换成处理系统格式,加载到磁盘上;2、输入数据质量检查:炮号、道号波形、道长、采样间隔等等。
二、置道头●道头: 每个地震道的开始部分都有个固定字节长度的空余段,这个空余段用来记录描述本道各种属性的信息,称之为道头。
如第8炮第2道,第126MP等。
观测系统定义:定义一个相对坐标系,将野外的激发点、按收点的实际位置放到这个相对的坐标系中。
观测系统定义完成后,处理软件中置道头模块,可以根据定义的观测系统,计算出各个需要的道头字的值井放入地震教据的道头中。
当道头置入了内容后,我们任取道都可以从道头中了解到这一道属于哪炮、哪一道? CIP号是多少?炮检距是多少?炮点静校正量、检波点静校正量是多少等。
后续处理的各个模块都是从道头中获取信息,进行8的处里,如抽MP道集,只要将数据道头中cmP号相同的道排在一起就可以了因此道头有错误,后续工作也是错误的。

实验三 地震反演技术一、实验目的1. 了解地震反演技术的基本理论和方法2. 了解利用STRATA 软件进行波阻抗反演的基本过程二、实验内容与过程1. 褶积模型反演的基本模型就是褶积模型,用公式可以表达为:)()1()()(i n j i W j r i •T j++-=∑ 简单地说,反演的过程就是在已知地震道记录的)(i T 的条件下,通过估计子波来求取反射系数)(j r 的过程。
2. 反射系数与波阻抗反射系数与地层波阻抗的关系可以表达如下:)1()()1()()(-+--=j I j I j I j I j r 其中,)()()(j V j j I ρ=,ρ为密度,V 为速度。
因为反射系数是受速度和密度两个因素的影响,并不是单单取决于其中的某一个因素,因此在叠后反演中无法分离速度和密度,仅能衡量波阻抗的变化,即STRATA 的反演最终结果实际上是一系列波阻抗道。
3. 地震子波的估计与提取为了进行波阻抗的反演,需要提取地震子波,利用褶积模型来求取反射系数,通常提取子波的类型有以下三大类:(1)纯确定法,即用地表检波器或其他仪器直接测量直接测量子波;(2)统计法,完全依靠地震资料的自相关来求取地震子波;(3)使用测井曲线法,即使用测井和地震数据结合。
本次实验着重使用统计法提取子波,即利用地震资料来估计子波,如下图:地震子波的时间响应地震子波的频率响应4.利用测井曲线作为约束条件进行反演使用G4井的测井曲线作为约束条件,内插外推,进行波阻抗反演,得到G4波阻抗反演剖面:其中绿色的表示波阻抗较低的分界面,即3煤,其波阻抗切片图如下:5.反演质量的评价在一个参数选择合理、约束条件选取适当的反演中,合成记录与实际地震记录的匹配程度会很高,即两者之间的误差很小,同时反演结果与初始猜测模型的偏离程度也不会很大。
但是受测井资料的原始采集误差及转换误差的影响,在大多数情况下这两种尺度是相矛盾的,在追求合成记录与实际地震资料高精度匹配的同时,必然会增大最终反演结果与初始猜测模型的偏离程度。



地震子波处理的二步法反褶积方法研究
地震子波处理的二步法反褶积方法研究
针对玛湖斜坡区三块三维地震资料和赛汉塔拉凹陷二块三维地震资料连片处理中的特点,结合地质任务和处理目标要求,提出了地震数据连片处理中的地震子波处理的方法.该方法主要体现了两次反褶积,一次是采用地表一致性反褶积,将不同震源的频带拓宽到一个标准上;再一次采用相位校正反褶积,将不同震源的数据校正到相同相位上.为了保证提取的相位校正反褶积算子稳定,采用叠后地震道提取(主要考虑到叠后地震道信噪比高,算子稳定性强),然后将该算子应用到叠前地震道,进行相位校正.
作者:王西文胡自多田彦灿王红旗王述江肖明图马建华WANG Xi-wen HU Zi-duo TIAN Yan-can WANG Hong-qi WANG Shu-jiang Xiao Ming-tu Ma Jian-hua 作者单位:中国石油勘探开发研究院西北分院,兰州,730020 刊名:地球物理学进展ISTIC PKU英文刊名:PROGRESS IN GEOPHYSICS 年,卷(期):2006 21(4) 分类号:P631 关键词:连片处理子波处理地表一致性反褶积相位校正。

地震资料处理中串联组合反褶积方法及效果分析作者:王博睿张雪纯来源:《中国科技纵横》2018年第19期摘要:地震资料处理过程中,反褶积是一种常用的提高地震资料分辨率的处理方法。
但由于提高分辨率处理是一个多次试验和逐步提高的过程,因此经常采用串联组合反褶积的处理方式。
由于各种反褶积都有一定的假设前提和各自的适用范围,所以必须根据数据的特点和不同反褶积的使用前提,经过详细而充分的试验以便选取最合理的参数,才能最终得到较好的处理效果。
采用哪种反褶积,怎样组合,才能达到搭配合理、纵向分辨率高的处理结果,常常需要通过细致的多种组合试验来确定。
本文叙述了实际资料处理中的反褶积串联组合的基本流程和实际资料的处理效果,并对一些反褶积方法组合方式及参数选择应注意的问题进行了探讨。
关键词:反褶积;分辨率;信噪比中图分类号:P631.4 文献标识码:A 文章编号:1671-2064(2018)19-0185-031 引言反褶积是通过压缩地震子波来提高地震记录纵向分辨率的主要方法,是处理流程中不可或缺的一部分。
反褶积前应对数据做好野外静校正、折射波静校正、尽可能地压制各种干扰、做好振幅补偿。
比较常用的反褶积方法有预测反褶积、俞氏子波反褶积、两步法统计子波反褶积、地表一致性反褶积、逐点反褶积等。
选用地表一致性反褶积、预测反褶积和统计子波反褶积作为此次组合试验的三种反褶积方法,试验了各种反褶积方法的参数选择以及它们不同串联组合方式下的效果,对结果进行频谱分析与自相关分析并结合剖面上的对比,最后选出频带宽、纵向分辨率高等综合效果好的串联组合方式,并在中国东部某地的实际资料处理中得到了比较好的效果,从而证明了本次处理采用的串联组合反褶积方法的正确性和实用性。
2 反褶积的原理2.1 地表一致性反褶积地表一致性反褶积主要用于消除由于激发、接收等因素引起的地震记录间子波的差异,采用自回归谱分析方法,以对数方式计算每个输入道的对数功率谱[1]:(1)自回归过程的功率谱为:(2)其中:(3)以地表一致性方式分解对数功率谱成为震源、检波点、炮检距中点和偏移距分量。


地震资料处理中子波的有效提取和反褶积计算孔维新【摘要】提取地震子波是数据分析和处理的关键,采用不同的子波提取计算方法,比较不同算法求取子波同原始子波间的差异,分析其原因和问题所在;另外通过反褶积获取新的地震记录,对比剖面分辨率的变化情况.其主要目的是提供相关处理参数的算法,比较之间的差异和优劣,寻求最佳匹配算法,计算精度是本文的重点.【期刊名称】《工程地球物理学报》【年(卷),期】2011(008)005【总页数】9页(P579-587)【关键词】反褶积;子波;算法【作者】孔维新【作者单位】中国石化西南石油局第五物探大队,湖南湘潭411104【正文语种】中文【中图分类】P631.3地震波在传播中,受到地层介质的滤波作用,使得垂向分辨率极大降低;而反褶积(deconvolution)又称反滤波(inverse filter),是能消除这种滤波作用,尽量恢复激发信号波的处理方法,它是一种通过压缩基本子波来提高地震数据垂向分辨率的处理过程。
在理想情况下,反褶积能压缩子波长度并衰减多次波,最后在地震道上仅仅保留地下反射系数(Yilmaz,1987)[1]。
而反褶积的实现需要知道反滤波因子,而这得先知道其地震子波,但地震子波的准确求取是个难点。
本文就提取子波的不同算法进行介绍,并对这些算法提取的子波进行对比分析,得出Claerbout提取子波法较合适的结论。
同时本文的论证过程也可为实际地震资料处理提供一些计算思路和办法。
目前提取子波的方法主要有直接观测法(只适用于海上勘探)、自相关法(Wold -Kolmogorov法)[2]、Claerbout算法、多项式求根法(无法处理单位圆上的根)、同态滤波法[3](抗噪声能力弱,但没有苛刻的假设条件,只要求子波的对数谱和反射系数的对数谱序列在时间上可分,本试验采用同态滤波的递归实现方式)以及利用测井资料提取子波(只适应于有井区域,可通过谱除法和最小平方法求解)等方法。

第二章 反褶积将地震记录看成是反射系数序列与地震子波的褶积,反褶积就是要消除这种褶积过程,从地震记录得到反射系数序列。
一般说来,反褶积的目的是消除某种已知的或未知的褶积过程的运算。
反褶积也可能用来消除震源信号或者记录仪器的响应。
反褶积也可能是用另一种褶积过程代替原来的褶积过程。
反褶积是一种滤波。
与一般滤波的区别有两点:一是着眼点在改变子波,而不是衰减噪声。
二是方法上是根据需要达到的目标由地震资料自动推导滤波器,而不是通过试验选择滤波器。
反褶积是子波级的处理,是常规处理中最精细的环节。
一 子波与反褶积原始记录上的子波不管如何千变万化,必然是单边子波。
可控震源原始记录上的子波也是单边的,即扫描信号,经过相关以后才变成双边子波。
单边子波是物理可实现的,双边子波是非物理可实现的。
单边子波可以是最小相位子波、最大相位子波或混合相位子波。
判别方法可以有很多,对于下面的讨论来说,用Z 变换大概是最方便的。
将子波的各个样点值作为系数、样点序号作为Z 的幂次,写成Z 多项式,如果Z 多项式的根的模全部大于1,即根全部在单位圆外,就是最小相位子波;如果Z 多项式的根全部在单位圆内,就是最大相位子波;如果Z 多项式的根有一些在单位圆外,有一些在单位圆内,就是混合相位子波。
Z 多项式可以因式分解,每个因式有01=+bZ 形式,它代表有一个根Z 1-=。
(b 可以是实数,也可以是复数。
如是复数,必然共轭成对出现。
)可见当1<b 时,这个因式是最小相位的;当1>b 时,这个因式是最大相位的。
如果所有因式是最小相位的,子波就是最小相位的;如果所有因式是最大相位的,子波就是最大相位的;如果有一部分因式是最小相位的,有一部分因式是最大相位的,子波就是混合相位的。
因此,最小相位子波的尾点的绝对值必然小于其首点的绝对值,最大相位子波的尾点的绝对值必然大于其首点的绝对值,混合相位子波则可以是任何情形。
根据这个简单规则,至少在看到尾点的绝对值大于首点的绝对值的子波时,立刻就能判断它绝对不可能是最小相位子波。
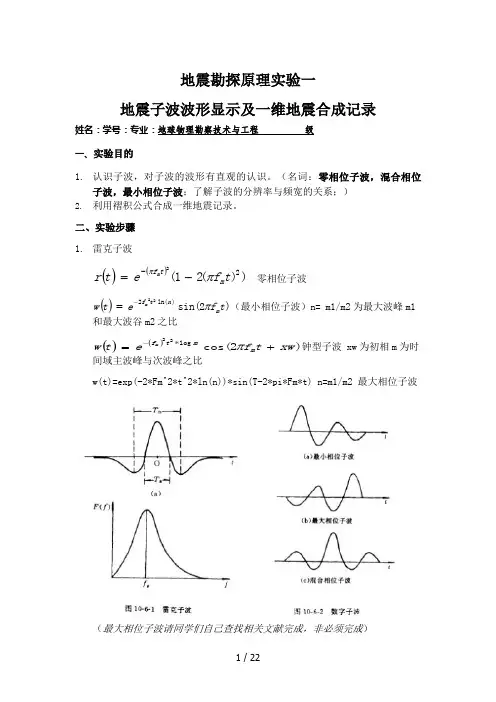
地震勘探原理实验一地震子波波形显示及一维地震合成记录姓名:学号:专业:地球物理勘察技术与工程 级 一、实验目的1. 认识子波,对子波的波形有直观的认识。
(名词:零相位子波,混合相位子波,最小相位子波;了解子波的分辨率与频宽的关系;) 2. 利用褶积公式合成一维地震记录。
二、实验步骤 1. 雷克子波()()))(21(22t f et r m t f m ππ-=- 零相位子波())2sin()ln(222t f et w m n t f m π-=(最小相位子波)n= m1/m2为最大波峰m1和最大波谷m2之比()())2cos(log *22xw t f et w m mt f m +=-π钟型子波 xw 为初相m 为时间域主波峰与次波峰之比w(t)=exp(-2*Fm^2*t^2*ln(n))*sin(T-2*pi*Fm*t) n=m1/m2 最大相位子波(最大相位子波请同学们自己查找相关文献完成,非必须完成)其中f代表子波的中心频率, t =i*dt,dt为时间采样间隔,i为时间m离散点序号; 这里可以为f = 10,25,40,100 Hz等,采样间隔dt=0.002m秒,i为0~256;2.根据公式编程实现不同频率的零相位子波的波形显示;不同中心频率的零相位子波图f = 25:mf = 100:m3.其地质模型为:设计反射系数)(n r (n=512),n 为地层深度,其中0.1)100(=r ,为第一层介质深度;7.0)200(-=r ,为第二层介质深度;5.0)300(=r ,为第三层介质深度;4.0)400(=r ,为第四层介质深度;6.0)450(=r ,为第五层介质深度;其它为0。
地震波在介质中传播,当到达介质分界面时,发生反射和透射,反射波被检波器接受,生成地震记录。
反射系数表示地震波在两层介质分界面的能量重新分配,如r(100)=1.0,表示地震波入射到分界面时,只有一种波,反射纵波(或反射横波)。
第二章反褶积反褶积是借助压缩基本地震子波来改善时间分辨率的一种处理过程。
为搞清这一过程要求综合研究正演问题,即必须首先研究记录的地震道的积木式分段单元。
地层是由不同类型岩性的岩层组成的,每种岩石类型都有地球物理学家所可利用的某种物理特性。
至于地震勘探,则根据波传播速度和岩层密度确定岩层。
密度与速度的乘积称之为地震波阻抗,地震资料分析期望的最终成果就是地震波阻抗剖面。
我们有在井中直接检测岩层速度和密度的方法,这种方法能向我们提供地震波阻抗与深度的关系。
在地面上沿测线记录到的地震反射波就是由于两地层之间的波阻抗差引起的。
记录到的反射记录可通过反射率与震源子波的褶积来模拟。
下面分别对褶积模型、各种反滤波进行介绍,并给出应用实例。
2.1 褶积模型我们从图1给出的一个实际声测井记录入手,该声测井曲线是层速度与深度的关系图。
实际的速度测量是以 2英尺的采样间隔在1000-5400英尺之间的深度段内完成的。
借助简单的斜坡把速度函数外延至地面。
该声测井记录显示出明显突变和强低频趋势特征,这两者构成了总的速度变化。
实际上我们通常用CMP道集作速度分析进行估算的就是这种低频趋势。
对声测井曲线可通过人工分段提取其速度趋势,其结果可列表如下:由声测井记录确定的层速度趋势表1地层序号层速度(ft/s)深度范围(ft)1 21000 1000—20002 19000 ※2000—22503 18750 2250—25004 12650 2500—37755 19650 3775—5400※实际上该层速度是逐渐减小的。
我们所做的就是形成一组恒定层速度的层组。
把测井曲线进行这种分段多少有点类似于地质家对假想的地下模型所做的分层。
地质家是根据岩性分层,而我们根据声测井曲线的分段性质提取的分层则是以速度差为依据的。
下面对表1中所确定的地层的岩性分类:地层序号岩性1 2 3 灰岩泥质灰岩(泥岩含量逐渐增加) 泥质灰岩4 5 泥岩白云岩在声测井曲线的低频趋势上附加有高频分量。
地震子波与反射系数褶积 c++
地震子波与反射系数褶积在地球物理学中是一个重要的概念,
它们在地震数据处理和解释中起着关键作用。
子波是地震波在地下
介质中传播和反射后形成的波形,而反射系数则代表了地下介质的
变化对地震波的反射和透射的影响。
褶积则是一种数学运算,用于
描述两个函数之间的关系,对于地震子波与反射系数的褶积,可以
通过数学运算来模拟地震波在地下介质中的传播和反射情况。
在C++中,可以通过编写相应的程序来实现地震子波与反射系
数的褶积。
首先,需要定义表示地震子波和反射系数的函数或数组,并实现褶积运算。
可以使用C++中的数组和循环结构来处理地震子
波和反射系数的数据,并进行褶积运算。
此外,还可以利用C++中
的一些数学库函数来简化计算过程,例如STL中的向量和算法库,
或者使用第三方的数学库。
另外,在实现地震子波与反射系数的褶积时,需要考虑到数据
的边界处理、采样间隔、时间窗口等因素,以确保计算的准确性和
可靠性。
同时,还可以考虑使用并行计算来加速褶积运算的过程,
提高计算效率。
总之,地震子波与反射系数的褶积是地球物理学中重要的计算方法,通过在C++中实现相应的程序,可以对地震数据进行处理和解释,为地下介质的结构和性质提供重要的信息。
希望这个回答能够帮助你更好地理解和实现地震子波与反射系数的褶积。
反褶积处理方法论文提要反褶积即反滤波是常用的地震资料处理方法。
反褶积的目的是由地震数据恢复反射系数。
反滤波的作用主要是压缩地震反射脉冲的长度,提高反射地震记录的分辨能力,并进一步估计地下反射界面的反射系数。
这不仅是常规地震资料处理所需要的,而且是对直接找油找气的亮点技术和岩性研究的地层地震学的地震资料处理尤为重要。
另外,反滤波还可以清除短周期鸣震和多次波等干扰波。
当前地震资料处理解释已经基本实现了数据化、自动化,我国各大解释公司、研究所、高等院校都已有了较为先进数字化处理软件,在处理数字化的地震数据时表现出了很好的速度性和准确性。
反褶积可分为确定性反褶积和估计性反褶积两种。
目前常用的反褶积有最小平方反褶积、预测反褶积、同态反褶积、地表一致性反褶积、最大熵反褶积、变模反褶积、Q反褶积等等;特殊的反褶积有Noah反褶积、最小信息反褶积等。
正文一、反褶积(一)研究目的和意义1、研究目的(1)弄清各种反褶积处理方法的原理。
(2)弄清反褶积处理模块的参数意义。
(3)掌握地震资料数字处理的基本流程及处理方法。
(4)完善反褶积方法,提高地震资料处理的分辨率,保持信噪比,振幅均匀化。
2、研究意义反褶积是地震资料数字处理流程中最关键的一环,也是提高地震勘探分辨率最有效的方法。
一个处理流程包括许多处理步骤。
而每一个处理步骤又要涉及到好几个处理模块。
一个处理流程通常由预处理、叠前处理和叠后处理三部分组成。
其中反褶积是最重要的一个部分,如图1所示。
反褶积的目的就是为了分离子波和反射系数序列。
子波就像无线电中的载波,反射系数序列就像无线电中的声波。
只有消除高频载波才能提取声波。
子波在地层中传播,携带着反射系数序列这种有用的地质信息返回地面,只有消除子波才能恢复反射系数序列的本来面目。
反射系数序列中有波阻抗随时间变化的信息,这就提供了速度和密度随时间变化的信息,随之就可得到地层、岩性及构造在地下中间分布的信息。
在有利条件下还可得到岩石孔隙率、渗透率、孔隙流体性质(油、气、水)乃至地层压力的信息。
反褶积处理方法论文提要反褶积即反滤波是常用的地震资料处理方法。
反褶积的目的是由地震数据恢复反射系数。
反滤波的作用主要是压缩地震反射脉冲的长度,提高反射地震记录的分辨能力,并进一步估计地下反射界面的反射系数。
这不仅是常规地震资料处理所需要的,而且是对直接找油找气的亮点技术和岩性研究的地层地震学的地震资料处理尤为重要。
另外,反滤波还可以清除短周期鸣震和多次波等干扰波。
当前地震资料处理解释已经基本实现了数据化、自动化,我国各大解释公司、研究所、高等院校都已有了较为先进数字化处理软件,在处理数字化的地震数据时表现出了很好的速度性和准确性。
反褶积可分为确定性反褶积和估计性反褶积两种。
目前常用的反褶积有最小平方反褶积、预测反褶积、同态反褶积、地表一致性反褶积、最大熵反褶积、变模反褶积、Q反褶积等等;特殊的反褶积有Noah反褶积、最小信息反褶积等。
正文一、反褶积(一)研究目的和意义1、研究目的(1)弄清各种反褶积处理方法的原理。
(2)弄清反褶积处理模块的参数意义。
(3)掌握地震资料数字处理的基本流程及处理方法。
(4)完善反褶积方法,提高地震资料处理的分辨率,保持信噪比,振幅均匀化。
2、研究意义反褶积是地震资料数字处理流程中最关键的一环,也是提高地震勘探分辨率最有效的方法。
一个处理流程包括许多处理步骤。
而每一个处理步骤又要涉及到好几个处理模块。
一个处理流程通常由预处理、叠前处理和叠后处理三部分组成。
其中反褶积是最重要的一个部分,如图1所示。
反褶积的目的就是为了分离子波和反射系数序列。
子波就像无线电中的载波,反射系数序列就像无线电中的声波。
只有消除高频载波才能提取声波。
子波在地层中传播,携带着反射系数序列这种有用的地质信息返回地面,只有消除子波才能恢复反射系数序列的本来面目。
反射系数序列中有波阻抗随时间变化的信息,这就提供了速度和密度随时间变化的信息,随之就可得到地层、岩性及构造在地下中间分布的信息。
在有利条件下还可得到岩石孔隙率、渗透率、孔隙流体性质(油、气、水)乃至地层压力的信息。
地震资料数字处理Ⅱ实习报告一、实习内容已知声波测井数据(声波时差t ∆微秒/每英尺)、密度测井数据(岩层密度ρ克/每立方厘米)、测量点井深h (米)和地震子波数据,编程计算: (1)反射系数; (2)合成地震记录;(3)根据合成地震记录计算子波与反子波; (4)利用反子波与地震记录进行褶积(反褶积)。
二、基本方法原理1.计算反射系数的原理 (1)层速度i v 的计算原理i i t v ∆⨯=6103048.0(m/s ), N i ,,3,2,1 =,i 为测井数据序号, i t ∆代表第i 层的声波时差,i v 代表第i 层的层速度,N 为测井数据的长度。
本次实习中采用的模型Model.txt 中声波及密度数据的深度为600m 到2078.1m ,间隔0.1m 。
(2)垂直往返旅行时的计算原理i t 为第i 层的垂直往返旅行时,初始值取为: (3)反射系数的求取原理首先,根据测井资料直接求取反射系数:将声波测井数据单位由us/f 转化为m/s ,由ii i i ii i i i v v v v r ρρρρ+-=++++1111,1,,3,2,1-=N i ,i r 为第i 层的反射系数或者垂直往返旅行时为i t 处的反射系数,此反射系数是直接按测井数据计算未进行稀疏采样的。
根据上述方法计算得出的反射系数为深度域上的,即反射系数是随线性增加的地层1,,3,2)(211-=-+=+-N i V H H t t ii i i i 1112V H t =深度而变化,为了进行褶积来合成地震记录,必须将反射系数转换到时间域。
根据各层的旅行时和深度与速度的数值,只需计算出时间域上所对应的采样间隔,即可作出深时转换。
本次报告所采用的方法是三次样条函数插值的方法。
2. 合成地震记录原理如果已知地震子波)(t w 和反射系数)(t r ,则可以通过褶积模型来合成地震记录,如果考虑噪声影响,可得合成的人工地震记录:()()*()()x t w t r t n t =+,本次实习报告中为了简化运算难度,将忽略噪声影响。
盲信号实验报告盲解卷积算法姓名:丁宪成系别:电信学院专业:电磁场与微波学号:3110035012指导教师:陈文超2011年07月13日盲解卷积算法1. 原理:几个重要概念:1.1 褶积模型假设:假设1:地层是由具有常速的水平层组成;假设2:震源产生一个平面压缩波(P 波),法向入射到层边界上,在这种情况下,不产生剪切波(S 波);假设3:震源波形在地下传播过程中不变,即它是稳定的; 假设4:噪音成分是零;假设5:震源波形是已知的;假设6:反射系数序列是一个随机过程。
这意味着地震记录具有地; 震子波的特征,即它们的自相关和振幅谱是相似的;假设7:地震子波是最小相位的,因此,它有一个最小相位的逆。
1.2 反滤波如果定义滤波算子为f (t),则f (t) 与已知地震记录x(t)的褶积得到一个对地层脉冲响应e(t)的估计e(t) = f (t)∗ x(t); (1) x(t) = w(t)* f (t)* x(t); (2) δ(t) = w(t)* f (t); (3)1()()*()f t t w t δ= (4) 用流程图表示为:1.3 震源反子波计算震源反子波在数学上是利用z 变换来实现的。
例如,假设基本子波为两点时间序列(1,-0.5)1()12w z z =-2111()1 (12412)F z z z z ==+++-; (5) 2111()1 (12412)F z z z z ==+++- (6) ()F z 的系数11(1,,,...)24代表逆滤波算子f(t)有关的时间序列。
可以看出它有无限多个系数,然而它们递减的很快。
如同任何滤波过程一样,实际应用的算子都是被截断的。
1.4 最小平方反滤波当输入子波良好,其z 变换的逆可以用一收敛序列表示,则上面所描述的反滤波将得到一个很好的近似于尖脉冲的输出.将下面问题列出方程式:给定输入子波(1-0.5),寻找一个二项滤波器(a,b),使实际输出与期望输出(1,0,0)之间的误差在最小二乘的意义上最小。
将滤波器(a,b)与输入子波(1,-0.5)褶积以计算实际输出。
误差的累积能量L 定义为实际的与期望的输出的系数之差的平方和:222(1)()()22a b L a b =-+-+- (7) 目的是寻找系数(a,b)使L 最小,这要求变量L 随系数(a,b)而变并使之为零对上式进行简化,取L 对a 和b 的偏导数,并使其为零,得到: 522502a b a b ⎧-=⎪⎪⎨⎪-+=⎪⎩(8) 有两个方程和两个未知数即滤波器系数(a,b),可变成下列普通矩阵形式:5/21215/20a b -⎛⎫⎛⎫⎛⎫= ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭(9) 求解滤波系数,我们得到(a,b)为(0.95,0.38)。
1.5 最佳维纳滤波器回顾研究反滤波和最小平方滤波时讨论的期望输出,即零延迟尖脉冲(1,0,0)。
重写最小平方反滤波的求解方程如下:5/41/2221/25/40a b -⎛⎫⎛⎫⎛⎫= ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭(10) 两边同时除以2得到:上述结论被维纳普遍化以推导出将输入转换为任意期望输出的滤波器(Robinson 和Treltel ,1980)。
一个滤波器长度为n 的矩阵方程的普遍形式是:(11)式中i r 、i a 和i g (i =0,l,2,3,…,n -1)分别为输入子波自相关、维纳滤波系数和期望输出与输入子波的互相关。
其计算过程的流程图可以用下面图形表示为:与最小平方滤波的联系:最佳维纳滤波器0121(,,,...)n a a a a -是最佳的,是指它的实际输出与期望输出之间的最小平方误差最小。
当期望输出是零延迟尖脉冲(1,0,0,…,0)时,维纳滤波与最小平方滤波相同,即后者是前者的特例。
1.6 脉冲反褶积第一类期望输出(零延迟尖脉冲)的处理称为脉冲反褶积。
期望脉冲 (1,0,0,…,0)与输入子波011(,,...,)n x x x -的互相关得到序列(1,0,0,…,0)。
正则方程的一般形式改写成特殊形式:(12) 方程已用作了归一化。
在前面讨论过的最小平方反滤波器有与矩阵方程相同的形式。
因此,脉冲反褶积在数学上是与最小平方反滤波相同的。
而在实际上两类滤波器有一些区别。
在脉冲反褶积(统计反褶积)的情况,方程在左边的自相关矩阵由输入地震记录(假设6)求得,而在最小平方反滤波(确定性反褶积)的情况则直接由已知的震源子波求得。
结论:如果输入子波不是最小相位,则脉冲反褶积不能将它转化为完全的零延迟尖脉冲。
虽然振幅谱实质上是平的,但输出的相位谱不是最小相位的。
而且脉冲反褶积算子是输入子波的最小相位对应的子波的逆,这个子波可以是也可以不是最小相位的。
1.7 整形子波滤波器处理脉冲反褶积将子波(-0.5,1)压缩为零延迟尖脉冲(1,0,0)时有些困难。
从能量分布来说,这个输入子波更接近于延迟尖脉冲,如(0,1,0),而不是零延迟尖脉冲(1,0,0)。
或者,将子波(-0.5,1)转换为延迟尖脉冲的滤波器会比将它整形为零延迟尖脉冲的滤波器产生更少的误差。
根据最佳维纳滤波器的流程图重新设计和应用一个滤波器(期望输出为(0,1,0))。
首先,计算互相关。
我们知道输入子波的自相关。
将互相关和子波自相关的结果代入前述矩阵方程,得到:(13)求解滤波器系数,结果为162(,)(,)2121a b=-。
这个滤波器用于输入子波,如下表所示。
和我们期望的一样,输出结果与最小平方滤波的输出结果一样。
可以看出,对于延迟尖脉冲,实际输出与期望输出的最小平方误差为0.190;而对期望输出的零延迟尖脉冲,最小平方误差为0.762。
这表明,将子波(-0.5,1)转换为延迟尖脉冲(0,1,0)比零延迟尖脉冲(1,0,0)误差小。
2.实验内容地震记录信号是地震子波与地层脉冲响应相卷积的结果,如果我们要想得到脉冲信号必须进行盲解卷积,地震子波一般可以近似测得,我们要做的就是求出地震子波对应的逆信号,理想情况它们相卷积的结果为单位脉冲。
地震子波有零相位子波,最小相位子波,混合相位子波和最大相位子波,如下图所示:程序说明:在下面的程序中,我们任意给定一个模拟地震子波,通过一系列的操作得到想要得到的结果。
算法如下:第一步:产生模拟地震子波信号,给出预白百分比;第二步:给定期望输出,计算输入的自相关序列以及输入和期望输出的自相关序列;第三步:根据输入信号的自相关序列和预白百分比产生Toeplitz矩阵,根据Toeplitz矩阵和互相关序列求出维纳滤波器的滤波系数;第四步:通过将输入序列和滤波系数卷积求的实际输出。
3.实验结果:3.1 得到任意延迟脉冲信号:输入想得到的延迟脉冲的延迟时间:0(零延迟脉冲)输入想得到的延迟脉冲的延迟时间:5任意输出延迟时间,可以得到任意延迟的脉冲。
3.2 得到任意提前的输入序列运行结果:输入想得到的提前了的时间:2输入想得到的提前了的时间:10可见,提前的时间越长,得到的结果误差越来越大。
3.3 得到0相位子波运行结果:从对比图也可以看出在输入序列能量集中的地方得到的实际输出和期望输出误差比较小,其它区域误差较大。
3.4 得到任意期望输出:从对比图也可以看出,在输入子波能量集中的地方得到的实际结果与期望输出很近似,在输入子波幅度很小的区域得到的实际输出结果误差很大。
3.5 得到均方误差最小的实际输出运行结果:j =13;min1=0.0015.4.讨论地震子波的相位对处理结果的影响地震数据处理的目地是将野外采集的地震记录用处理模块进行处理后得到成像好,分辨率高的地震剖面,地震记录可描述为地震子波与地层脉冲响应或地下反射系数的褶积。
就某种意义是那个讲,地震数据处理实际上就是一个对地震子波不断改造的过程。
地震子波经过傅立叶变换之后可以得到振幅谱和相位谱,因此在地震记录中可通过拓宽地震子波的振幅谱来提高地震剖面的分辨率,也可以通过改变地震子波的相位谱来达到提高分辨率的目的。
分辨率高的地震子波在频率域上表现为振幅谱尽可能的拓宽。
而具有同样振幅谱的地震淄博中,最小相位的地震子波分辨率最高。
实际地震数据处理中对地震子波相位特性有要求和影响的处理模块主要包括可控震源地震子波最小化,预滤波,叠前反褶积和叠后地震子波零相位化。
我们知道地震数据处理的母的是提高地震记录的信噪比和分辨率,得到高信噪比,高分辨率的地震剖面。
在频率域中表现为使得振幅频带尽可能宽且剩余子波是零相位的,在处理中有些模块对地震数据的子波相位要求有假设前提条件。
一般情况下,叠前反褶积输入的地震数据要求子波是最小相位的,若是零相位的需要进行最小相位化,根据相同的振幅谱零相位的子波分辨率最高的原则,需要对叠后数据的子波进行零相位化处理。
5 附录:5.1 得到想要的任意延迟脉冲t=0:1:30;x=sin(pi*(t-2)/6.4).*exp(-0.12*abs(t-2)); %产生模拟子波subplot(211);plot(t,x);m=length(x);p=0.005; %预白百分比i=input('输入想得到的延迟脉冲的延迟时间:');y=[zeros(1,i),1,zeros(1,2*m-2-i)]; %期望输出n=length(y);r_xx=xcorr(x); %计算子波的自相关A=fliplr(r_xx(1:m));R=toeplitz([(1+p/100)*A(1),A(2:length(A))]); %产生Toeplitz矩阵r_xy=xcorr(x,y); %输入和期望输出的互相关G1=fliplr(r_xy(1:n));G2=G1(1:m);h=inv(R)*G2'; %h为维纳滤波器系数z=conv(x,h'); %计算实际输出信号subplot(212);plot(z) %绘制满足最小均方误差的实际输出结果5.2 得到时间提前了的输入序列说明:假设输入是(1,2,3,4,5,6),提前时间为2个单位,那么得到的期望输出序列为(3,4,5,6,0,0,…),所以上面的程序只要修改一下期望输出即可,将下面两行程序:i=input('输入想得到的延迟脉冲的延迟时间:');y=[zeros(1,i),1,zeros(1,2*m-2-i)]; %期望输出修改为:i=input('输入想得到的提前了的时间:');y=[x(i+1:m),zeros(1,m+i-1)]; %期望输出5.3 得到零相位子波零相位子波:所谓零相位子波,就是子波序列进行傅立叶变换得到的结果全是正实数,因为正实数的相位为零,我们可以给定一个实偶序列,其傅立叶变换是正偶实数,则它肯定是零相位的,例如余弦序列,其傅立叶变换的结果就是正实数,所以是零相位的,那么程序就要修改为:t=0:1:30;x=sin(pi*(t-1)/6.4).*exp(-0.12*abs(t-1)); %产生模拟子波subplot(311);plot(t,x);m=length(x);p=0.005; %预白百分比t1=-30:1:30;y=cos(pi*t1/30); %期望输出subplot(312)plot(y);n=length(y);r_xx=xcorr(x); %计算子波的自相关A=fliplr(r_xx(1:m));R=toeplitz([(1+p/100)*A(1),A(2:length(A))]); %产生Toeplitz矩阵r_xy=xcorr(x,y); %输入和期望输出的互相关G1=fliplr(r_xy(1:n));G2=G1(1:m);h=inv(R)*G2'; %h为维纳滤波器系数subplot(313);plot(z) %绘制满足最小均方误差的实际输出5.4 得到任意期望的输出期望输出可以用随机数产生,程序改为:t=0:1:30;x=sin(pi*(t-2)/6.4).*exp(-0.12*abs(t-2)); %产生模拟子波subplot(311);plot(t,x);m=length(x);p=0.005; %预白百分比y=rand(1,2*m-1); %期望输出subplot(312);plot(y);n=length(y);r_xx=xcorr(x); %计算子波的自相关A=fliplr(r_xx(1:m));R=toeplitz([(1+p/100)*A(1),A(2:length(A))]); %产生Toeplitz矩阵r_xy=xcorr(x,y); %输入和期望输出的互相关G1=fliplr(r_xy(1:n));G2=G1(1:m);h=inv(R)*G2'; %h为维纳滤波器系数subplot(313);plot(z) %绘制满足最小均方误差的实际输出结果5.5 得到均方误差最小的实际输出上面几个程序都是在期望输出给定的情况下求的的,但实际上如果输入子波为最大相位,期望输出又是无延迟的脉冲,得到的实际结果往往和期望输出误差相差很大,所以如果要得到较好的实际输出,我们可以通过对期望输出做一定的延迟来得到最优化的结果,这里的最优化就是最小均方误差。