信号与系统第二次讨论课

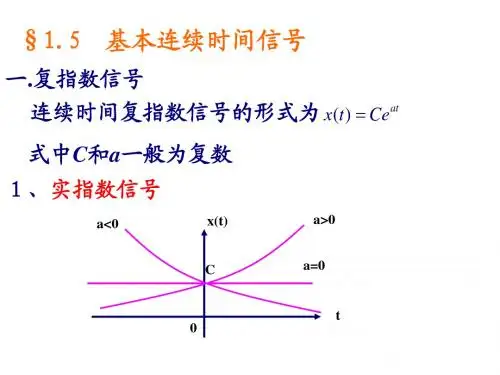
§1.5 基本连续时间信号一.复指数信号连续时间复指数信号的形式为()at x t Ce式中C 和a 一般为复数１、实指数信号x(t)ta>0a<0a=0C 0１）a <0因为a 在指数上，它小于０，说明x (t )随t 指数衰减２）a >0x (t )随时间t 而指数增加３）a =0此时x (t )==C 为一直流信号0Ce ２、虚指数信号tj e t x 0)(ω=这时01,C a j ω==这种信号具有如下特点0T １）它是周期为的周期信号002ωπ=T这是因为tj T j t j T t j e e e e 000000)(ωωωω=⋅=+2）它是复信号tj t e t x t j 00sin cos )(0ωωω+==有实部，也有虚部3）它的实部和虚部都是实数信号，而且具有相同基波周期{}t e t j 0cos Re 0ωω={}te t j 0sin Im 0ωω=3、复指数信号()atx t Ce =这时，C 和a 都是复数j C C e θ=0ωj r a +=00()cos()sin()rt rt x t C e t j C e t ωθωθ=+++r 代表振荡的包络r >0幅度增加r <0幅度减小0ω代表振荡的角频率{}0()0cos()Re j t A t A e ωθωθ++={}0()0sin()Im j t A t A e ωθωθ++=这是我们经常用到的正弦信号二、单位阶跃和单位冲激信号1、单位阶跃信号（单位阶跃函数）（1）定义式u (t )=0 t <01 t >010t u (t )t 0t 10此函数在t =0处不连续，它从0跳变到1，此点未定义，或定义为212)0()0()0(=+=+-u u u =-)(0t t u 延时阶跃函数：延时的单位阶跃函数定义为0t 1 t >0 t <0t tAu (t )表示信号A 在t =0处接入系统A 表示信号A 在时刻接入系统)(0t t u -0t t =例：tu (t -2)tu (t -2)2t（2）u (t )函数的作用1）通常把u (t )表示为信号作用的起始时间，how ？2）常用延迟阶跃函数u (t-t 0)的加权和来表示一些阶梯信号20468246x (t )t x (t )=4u (t -2)+2u (t -6)-6u (t -8)升做加（升几加几）Other examples: 矩形脉冲(p.14图1-21)等。

信号与系统（郑君⾥）第⼆版讲义第⼆章第⼆章连续时间系统的时域分析第⼀讲微分⽅程的建⽴与求解⼀、微分⽅程的建⽴与求解对电路系统建⽴微分⽅程，其各⽀路的电流、电压将为两种约束所⽀配： 1.来⾃连接⽅式的约束：KVL 和KIL ，与元件的性质⽆关。

2.来⾃元件伏安关系的约束：与元件的连接⽅式⽆关。

例2-1 如图2-1所⽰电路，激励信号为，求输出信号。

电路起始电压为零。

图2－1解以输出电压为响应变量，列回路电压⽅程：所以齐次解为：。

因激励信号为，若，则，将其代⼊微分⽅程：所以，从⽽求得完全解：由于电路起始电压为零并且输⼊不是冲激信号，所以电容两端电压不会发⽣跳变，，从⽽若，则特解为，将其代⼊微分⽅程，并利⽤起始条件求出系数，从⽽得到：⼆、起始条件的跳变——从到1.系统的状态(起始与初始状态)(1)系统的状态：系统在某⼀时刻的状态是⼀组必须知道的最少量的数据，利⽤这组数据和系统的模型以及该时刻接⼊的激励信号，就能够完全确定系统任何时刻的响应。

由于激励信号的接⼊，系统响应及其各阶导数可能在t=0时刻发⽣跳变，所以以表⽰激励接⼊之前的瞬时，⽽以表⽰激励接⼊以后的瞬时。

(2)起始状态：，它决定了零输⼊响应，在激励接⼊之前的瞬时t=系统的状态，它总结了计算未来响应所需要的过去的全部信息。

(3)初始状态：跳变量,它决定了零状态响应，在激励接⼊之后的瞬时系统的状态。

(4)初始条件：它决定了完全响应。

这三个量的关系是：。

2.初始条件的确定（换路定律）电容电压和电感电流在换路（电路接通、断开、接线突变、电路参数突变、电源突变）瞬间前后不能发⽣突变，即是连续的。

时不变：时变：例电路如图2-2所⽰，t=0以前开关位于"1"已进⼊稳态，t=0时刻，开关⾃"1"转⾄"2"。

(1)试从物理概念判断、和、。

(2)写出t>0时间内描述系统的微分⽅程式,求的完全响应。

图2－2解(1)换路前电路处于稳态电感相当于短路，电感电流，电容相当于开路= 0，= = 0。

信号与系统第二次实验报告一、实验目的1、理解掌握LTI系统线性性和时不变性；2、熟悉掌握常用的用于系统时域仿真分析的MATLAB函数；3、牢固掌握系统的单位冲激响应的概念，掌握LTI系统的卷积表达式及其物理意义，掌握卷积的计算方法、卷积的性质；4、掌握利用MATLAB计算卷积编程方法，并利用所编写的MATLAB程序卷积的基本性质。

二、实验仪器信号与系统实验箱一台、双踪示波器一台、计算机一台三、预习要求（一）思考出要验证线性时不变系统基本特征所需要的方法步骤：（二）仿真前先把两信号卷积结果计算一下，画出波形。

四、实验原理及内容（一）线性时不变系统线性性：齐次性和叠加性同时满足1、验证线性性系统在输入信号x1（t）、x2（t）作用时的响应信号分别为y1（t）、y2（t），给定两个常数a，b，当输入型号为x（t）时系统响应信号是y（t），且满足：叠加性：x（t）=x1（t）+x2（t）y（t）=y1（t）+y2（t）齐次性：x（t）=ax1（t）y（t）=ay1（t）如上基本电路，分析过程为：2、验证时不变性输入型号为x（t）时系统响应信号是y（t），对一给定长数t0，当输入信号时x （t-t0）时，系统响应信号为y（t-t0）仍为上图，分析过程为：二、卷积的计算定义在不同时间段的两个矩形脉冲信号并完成卷积运算，分别绘制这两个信号及其卷积的结果图形，图形按照2x2分割成四个字图。

注意观察两个矩形脉冲信号持续时间变化。

（一）矩形信号卷积1、当两个信号脉冲持续时间相同时：①x=u(t+1/2)-u(t-1/2);h=u(t-1)-u(t-2)时的程序图如下：clear allclose allt0=-4; t1=4; dt=0.01;t=t0:dt:t1;x=u(t+1/2)-u(t-1/2);h=u(t-1)-u(t-2);y=dt*conv(x,h);subplot(221)plot(t,x),grid on,title('Signal x(x)'),axis([t0,t1,-0.2,1.2])subplot(222)plot(t,h),grid on,title('Signal h(x)'),axis([t0,t1,-0.2,1.2])subplot(212)t=2*t0:dt:2*t1;plot(t,y),grid on,title('The convolution of x(t) andh(x)'),axis([2*t0,2*t1,-0.1,1.2])xlabel('Time t sec')Signal x(x)Signal h(x)The convolution of x(t) and h(x)Time t sec②x=u(t+1/2)-u(t-1/2);h=u(t-2)-u(t-3)时的程序如下：clear all close allt0=-4; t1=4; dt=0.01; t=t0:dt:t1;x=u(t+1/2)-u(t-1/2); h=u(t-2)-u(t-3); y=dt*conv(x,h); subplot(221)plot(t,x),grid on ,title('Signal x(x)'),axis([t0,t1,-0.2,1.2]) subplot(222)plot(t,h),grid on ,title('Signal h(x)'),axis([t0,t1,-0.2,1.2]) subplot(212) t=2*t0:dt:2*t1;plot(t,y),grid on ,title('The convolution of x(t) and h(x)'),axis([2*t0,2*t1,-0.1,1.2]) xlabel('Time t sec')-4-224Signal x(x)-4-224Signal h(x)-8-6-4-202468The convolution of x(t) and h(x)Time t sec2、当两信号脉冲持续时间不相同时：①x=u(t+1/2)-u(t-1/2); h=u(t-1)-u(t-3)时，程序如下：clear all close allt0=-4; t1=4; dt=0.01; t=t0:dt:t1;x=u(t+1/2)-u(t-1/2); h=u(t-1)-u(t-3); y=dt*conv(x,h); subplot(221)plot(t,x),grid on ,title('Signal x(x)'),axis([t0,t1,-0.2,1.2]) subplot(222)plot(t,h),grid on ,title('Signal h(x)'),axis([t0,t1,-0.2,1.2]) subplot(212) t=2*t0:dt:2*t1;plot(t,y),grid on ,title('The convolution of x(t) and h(x)'),axis([2*t0,2*t1,-0.1,1.2]) xlabel('Time t sec')Signal x(x)Signal h(x)-8-6-4-22468The convolution of x(t) and h(x)Time t sec②x=u(t+1/2)-u(t-1/2);h=u(t+1)-u(t-1)时的程序如下：clear all close allt0=-4; t1=4; dt=0.01; t=t0:dt:t1;x=u(t+1/2)-u(t-1/2); h=u(t+1)-u(t-1); y=dt*conv(x,h); subplot(221)plot(t,x),grid on ,title('Signal x(x)'),axis([t0,t1,-0.2,1.2])subplot(222)plot(t,h),grid on ,title('Signal h(x)'),axis([t0,t1,-0.2,1.2]) subplot(212) t=2*t0:dt:2*t1;plot(t,y),grid on ,title('The convolution of x(t) and h(x)'),axis([2*t0,2*t1,-0.1,1.2]) xlabel('Time t sec')Signal x(x)Signal h(x)The convolution of x(t) and h(x)Time t sec据观察：当两距形脉冲持续时间相同时，卷积得到信号是三角波，脉冲持续时间是矩形波的两倍；当两距形脉冲持续时间不相同时，卷积得到信号是梯形波，脉冲持续时间是两矩形波持续时间的和； 波的幅值不变。

研讨课题目给定一个连续LTI 系统，其微分方程为：)()(25)()('''t x t y t y t y =++输入信号：()123sin2sin2sin2x t f t f t f tπππ=++(其中f1=0.05Hz ，f2=0.5Hz ，f2=3Hz)理论分析1)计算系统的幅度响应，判断该系统是哪一类频率选择性滤波器？（低通、高通、带通、带阻）因为25)(1)(2++=ωωωj j j Hωωωωωωωωωωωωωωωωωω225322422242242222222222251225511)2551(2549])25[()25()25()25()(+-++-=+-+-=--+-=----=j j H可以判断出该系统是低通滤波器 2)求系统的输出信号。

)26.36sin(003.0)73.11sin(07.0)73.01.0sin(04.0))(sin()())(sin()())(sin()()(313222111︒-+︒-+︒-=+++++=t t t t j H t j H t j H t y πππωφωωωφωωωφωω仿真分析MATLAB 仿真程序 ts=0; te=100; fs=10;t=ts:1/fs:te; N=1000;x=sin(2*pi*0.05*t)+sin(2*pi*0.5*t)+si n(2*pi*3*t);sbplot(231);plot(t,x);X=fft(x,N)/N;fx=(-(N-1)/2:(N-1)/2)/N*fs; subplot(234);plot(fx,abs(fftshift(X))); num=[1];den=[1 1 25];sys=tf(num,den);w=0:0.1:100;freqs(num,den,w);w=logspace(-1,2,100); [mag,pha]=bode(num,den,w); magdB=20*log10(mag); subplot(232);semilogx(w,magdB);grid on; subplot(235);semilogx(w,pha);grid on;y=lsim(sys,x,t);Y=fft(y)/fs;subplot(233);plot(t,y);Y=fft(y,N)/N;subplot(236);plot(fx,abs(fftshift(Y)) );绘制系统的频率响应Bode图绘制输入、输出信号的时域波形和频谱，分析和解释滤波过程;i）输入信号的时域波形输入信号的频谱理论计算：()()())6()6()()()1.0()1.0()(πωδπωδππωδπωδππωδπωδπω+--++--++--=jjjj X其中ππππππππ=⨯===-==-=25.0)6()6()()()1.0()1.0(j X j X j X j X j X j X仿真结果和理论计算相同。

《信号与系统》实验报告目录一、实验概述 (2)1. 实验目的 (2)2. 实验原理 (3)3. 实验设备与工具 (4)二、实验内容与步骤 (5)1. 实验一 (6)1.1 实验目的 (7)1.2 实验原理 (7)1.3 实验内容与步骤 (8)1.4 实验结果与分析 (9)2. 实验二 (10)2.1 实验目的 (12)2.2 实验原理 (12)2.3 实验内容与步骤 (13)2.4 实验结果与分析 (14)3. 实验三 (15)3.1 实验目的 (16)3.2 实验原理 (16)3.3 实验内容与步骤 (17)3.4 实验结果与分析 (19)4. 实验四 (20)4.1 实验目的 (20)4.2 实验原理 (21)4.3 实验内容与步骤 (22)4.4 实验结果与分析 (22)三、实验总结与体会 (24)1. 实验成果总结 (25)2. 实验中的问题与解决方法 (26)3. 对信号与系统课程的理解与认识 (27)4. 对未来学习与研究的展望 (28)一、实验概述本实验主要围绕信号与系统的相关知识展开，旨在帮助学生更好地理解信号与系统的基本概念、性质和应用。

通过本实验，学生将能够掌握信号与系统的基本操作，如傅里叶变换、拉普拉斯变换等，并能够运用这些方法分析和处理实际问题。

本实验还将培养学生的动手能力和团队协作能力，使学生能够在实际工程中灵活运用所学知识。

本实验共分为五个子实验，分别是：信号的基本属性测量、信号的频谱分析、信号的时域分析、信号的频域分析以及信号的采样与重构。

每个子实验都有明确的目标和要求，学生需要根据实验要求完成相应的实验内容，并撰写实验报告。

在实验过程中，学生将通过理论学习和实际操作相结合的方式，逐步深入了解信号与系统的知识体系，提高自己的综合素质。

1. 实验目的本次实验旨在通过实践操作，使学生深入理解信号与系统的基本原理和概念。

通过具体的实验操作和数据分析，掌握信号与系统分析的基本方法，提高解决实际问题的能力。