《信号与系统》第二次作业

(单选题)1: 当输入信号的复频率等于系统函数的零点时，系统的强迫响应分量为（）。

A: 无穷大
B: 不为零的常数
C: 0
D: 随输入信号而定
正确答案: C
(单选题)2: 满足傅氏级数收敛条件时，周期信号f(t)的平均功率（）。

A: 大于各谐波分量平均功率之和
B: 不等于各谐波分量平均功率之和
C: 小于各谐波分量平均功率之和
D: 等于各谐波分量平均功率之和
正确答案: D
(单选题)3: 卷积δ(t)*f(t)*δ(t)的结果为（）。

A: δ(t)
B: δ(2t)
C: f(t)
D: f(2t)
正确答案: C
(单选题)4: 信号的时宽与信号的频宽之间呈（）。

A: 正比关系
B: 反比关系
C: 平方关系
D: 没有关系
正确答案: B
(单选题)5: 设一个矩形脉冲的面积为S，则矩形脉冲的傅氏变换在原点处的函数值等于（）。

A: S/2
B: S/3
C: S/4
D: S
正确答案: D
(单选题)6: 线性系统具有（）。

A: 分解特性
B: 零状态线性
C: 零输入线性
D: 以上全对
正确答案: D
(单选题)7: 如果一连续时间二阶系统的系统函数H(s)的共轭极点在虚轴上，则它的h(t)应是（）。

《信号与系统》期末复习材料一、考核目标和范围通过考核使学生了解和掌握信号与系统的基本原理、概念和方法，运用数学分析的方法解决一些简单问题，使学生在分析问题和解决问题的能力上有所提高，为学生进一步学习后续课程打下坚实的基础。

课程考核的命题严格限定在教材第1—8章内，对第9、10章不做要求。

二、考核方式三、复习资源和复习方法（1）教材《信号与系统》第2版，陈后金，胡健，薛健编著，清华大学出版社，北方交通大学出版社，2003年。

结合教材习题解答参考书（陈后金，胡健，薛健，钱满义，《信号与系统学习指导与习题精解》，清华大学出版社，北京交通大学出版社，2005）进行课后习题的练习、复习。

（2）离线作业。

两次离线作业题目要熟练掌握。

（3）复习方法：掌握信号与系统的时域、变换域分析方法，理解各种变换（傅里叶变换、拉普拉斯变换、Z变换）的基本内容、性质与应用。

特别要建立信号与系统的频域分析的概念以及系统函数的概念。

结合习题进行反复练习。

四、期末复习重难点第1章信号与系统分析导论1. 掌握信号的定义及分类。

2. 掌握系统的描述、分类及特性。

3. 重点掌握确定信号及线性非时变系统的特性。

第2章信号的时域分析1．掌握典型连续信号与离散信号的定义、特性及其相互关系。

2．掌握连续信号与离散信号的基本运算。

3．掌握信号的分解，重点掌握任意连续信号分解为冲激信号的线性组合，任意离散信号分解为单位脉冲序列的线性组合。

第3章系统的时域分析1．掌握线性非时变连续时间系统时域描述。

2．掌握用卷积法计算连续时间系统的零状态响应3．掌握离散时间系统的时域描述。

4．掌握用卷积法计算离散时间系统的零状态响应。

第4章周期信号的频域分析1．掌握连续周期信号的频域分析方法。

2．掌握离散周期信号的频域分析方法。

第5章非周期信号的频域分析1．掌握常见连续时间信号的频谱，以及Fourier变换的基本性质及物理含义。

2．掌握连续非周期信号的频域分析。

3．掌握离散非周期信号的频域分析。

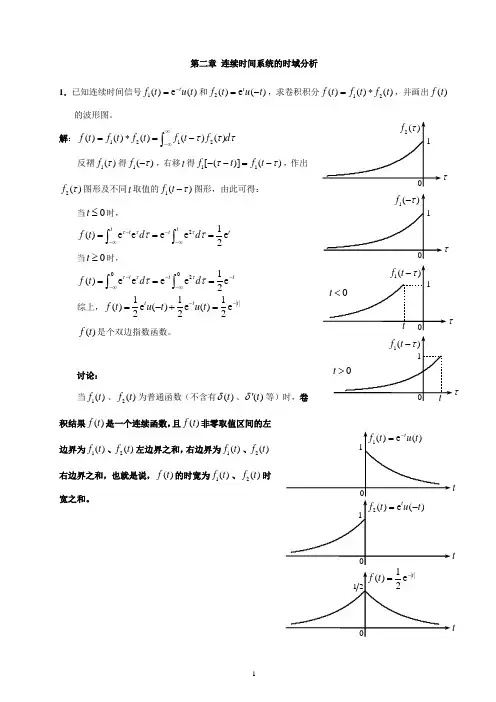
第二章 连续时间系统的时域分析1．已知连续时间信号1()e ()t f t u t -=和2()e ()t f t u t =-，求卷积积分12()()()f t f t f t =*，并画出()f t 的波形图。

解：1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰反褶1()f τ得1()f τ-，右移t 得11[()]()f t f t ττ--=-，作出2()f τ图形及不同t 取值的1()f t τ-图形，由此可得：当0t ≤时，21()e e ee e 2ttt tt f t d d τττττ---∞-∞===⎰⎰当0t ≥时，0021()e e e e e 2t t t f t d d τττττ----∞-∞===⎰⎰综上，||111()e ()e ()e 222t t t f t u t u t --=-+=()f t 是个双边指数函数。

讨论：当1()f t 、2()f t 为普通函数（不含有()t δ、()t δ'等）时，卷积结果()f t 是一个连续函数，且()f t 非零取值区间的左边界为1()f t 、2()f t 左边界之和，右边界为1()f t 、2()f t 右边界之和，也就是说，()f t 的时宽为1()f t 、2()f t 时宽之和。

τttt2．计算题图2（a ）所示函数)(1t f 和)(2t f 的卷积积分)()()(21t f t f t f *=，并画出)(t f 的图形。

解法一：图解法1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰其中1()f t τ-的波形见题图2(b)，由此可得： 当10t +≤，即1t ≤-时，()0f t = 当011t ≤+≤，即10t -≤≤时，120()2(1)t f t d t ττ+==+⎰当11t +≥但10t -≤，即01t ≤≤时，1()21f t d ττ==⎰当011t ≤-≤，即12t ≤≤时，121()21(1)t f t d t ττ-==--⎰当11t -≥，即2t ≥时，()0f t =综上，220,1,2(1),10()1,011(1),12t t t t f t t t t ≤-≥⎧⎪+-≤≤⎪=⎨≤≤⎪⎪--≤≤⎩ ()f t 波形见题图2(c)。

北航《信号与系统》在线作业二
试卷总分:100 得分:100
一、单选题 (共 10 道试题,共 30 分)
1. 连续周期信号的傅氏变换是 ________。

A. 连续的
B. 周期性的
C. 离散的
D. 与单周期的相同
满分：3 分
正确答案:C
2. 某系统的系统函数为 H （ s ），若同时存在频响函数 H （ j ω），则该系统必须满足条件 ________。

A. 时不变系统
B. 因果系统
C. 稳定系统
D. 线性系统
满分：3 分
正确答案:A
3. 欲使信号通过系统后只产生相位变化，则该系统一定是 ________。

A. 高通滤波网络
B. 带通滤波网络
C. 全通网络
D. 最小相移网络
满分：3 分
正确答案:C
4. 已知某连续时间系统的系统函数H（s）= 1/(s+1)，该系统属于什么类型 ________。

A. 高通滤波器
B. 低通滤波器
C. 带通滤波器
D. 带阻滤波器
满分：3 分
正确答案:B
5. 当输入信号的复频率等于系统函数的零点时，系统的强迫响应分量为 ________。

A. 无穷大
B. 不为零的常数
C. 0。

第10章Z变换习题10.1 试对下列和式，为保证收敛确定在r＝|z|上的限制：解:（a）为了保证收敛，需满足即使和式收敛的z均满足，亦即有又因在和式中含有一个正幂项z，故z≠∞。

综上所述，使和式收敛的z的模需满足为了保证收敛，需，即满足|2z|＜1，从而知使和式收敛的z的模需满足为了保证收敛，需，即|z|＞1；为了保证收敛，需，即|z|＞1综上所述，使和式收敛的z的模需满足r＞1。

对于上式右端第二项，要保证其收敛，需，即|z|＜2。

对于上式右端第三项，要保证其收敛，需，即|z|＜2。

对于上式右端第四项，要保证其收敛，需，即。

对于上式右端第五项，要保证其收敛，需，即。

综上所述，要使和式收敛，z的模需满足。

10.2 设信号x[n]为利用式（10-3）求该信号的z变换，并标出对应的收敛域。

解:为使该级数收敛，需，即，于是可得10.3 设信号x[n]为已知它的z变换x（z）的收敛域是试确定在复数α和整数n0上的限制。

解:令x[n]＝x1[n]＋x2[n]，其中x1[n]＝（－1）n u[n]，x2＝αn u[－n－n0]于是有则X（z）＝X1（z）＋X2（z），1＜|z|＜|α|由于已知X（z）的收敛域为1＜|z|＜2，所以α应满足|α|＝2，而n0可为任意整数。

10.4 考虑下面信号：对x（z）确定它的极点和收敛域。

解：因为，要使x（z）收敛，显然应有及，即X（z）的ROC为由于故X（z）的两个极点分别为，它们是互为共轭自两个复数极点。

10.5 对下列信号z变换的每个代数表示式，确定在有限z平面内的零点个数和在无限远点的零点个数。

解:（a）由于X（z）的分母多项式的阶数比分子多项式的阶数高1阶，所以X（z）在有限z平面上零点的个数为1（即X（z）的有限零点个数为1），同样在无穷远处的零点个数也为1。

由于x（z）的分母多项式与分子多项式有相同的阶数，所以X（z）仅有2个有限零点，而在无穷远处无零点。

由于X（z）的分母多项式的阶数比分子多项式的阶数高2阶，所以X（z）有1个有限零点，而在无穷远处有2个零点。

第二章部分习题参考答案2-6 试求下列各函数1()f t 与2()f t 之卷积。

121212(-)01(1) ()() ()() (0) ()()()(-) ()(-)11(1) 0(2) ()t tt t tt t f t u t f t e u t f t f t f f t d u eu t d e e d e e e t f t ααταατααταατττττττααδ-+∞-∞+∞---∞--==>*===⋅=⋅=-≥=⎰⎰⎰，解：，2121212() ()cos(45)()()()cos[()45] cos(45)(3) ()(1)[()(1)] ()(1)(2) ()()t f t t f t f t t d t f t t u t u t f t u t u t f t f t ωδτωττω+∞-∞=+*=-+=+=+--=---*⎰，解：，解：ττ222221211211()(-1)(-1)-2(-2)(-2)(-1)(-1)-(-2)(-2)2211-(-2)(-2)(-3)(-3)-(-2)(-2)(-3)(-3)22()*()()1,()0123, (1-)(1)21(1)--(12ttf t t u t t u t t u t t u t t u t t u t t u t t u t f t f t f t t f t t t dt t ft t t t τττ=+++=<=<<+=+-=++⎰222-112222212111)-222123, (1-)(1)-221()2(1)-2(1-)(-1)211121---152223, ()*()0.t t t t t t d t f t t t t t t t t t t t f t f t ττττ-+=<<+=+=+++=+++=++>=⎰121221--(4) cos , (1)-(-1)()*()()(-) [(1)-(-1)][cos(-)] cos[(1)]-cos[(-1)]f t t f t t t f t f t f f t d t t t d t t ωδδτττδδωττωω+∞∞+∞∞==+==+⋅=+⎰⎰ -212-212--2-220(5) ()(), ()sin ()()()*()()sin(-)(-) sin(-)sin t t ttt tf t e u t f t t u t f t f t f t e u t u t d e t d ee d τττττττττ+∞∞==⋅==⋅⋅⋅=⋅=⋅⎰⎰⎰-12-(-)--0022-(-)-33-2-3(6) ()2[()-(-3)], ()4()-(-2)0, ()0.02,()2488-825, 88()8(-)5, ()0.t tt t t tt t t t t f t e u t u t f t u t u t t f t t f t e d e e e t ft ed ef t e e e t f t ττττττ-==<=<<==⋅=<<===>=⎰⎰2-8 求阶跃响应为32()(21)()t t s t e e u t --=-+的LTI （线性时不变）系统对输入()()t x t e u t =的响应。

苏州大学 信号与系统 课程 第2次过程化考试参考答案 共 页一、 简算、填空与作图（每题4分，共40分）1、已知−→−F t f )()(j ωF ，则()(25)()F y t f t Y j ω=+−−→= 。

521()22j j ωF e ω 2、已知频谱)]()([)(00ωωδωωδπω-++=j F ，则原时间信号=)(t f 。

0cos()t ω3、3、已知周期信号()f t 前四分之一周期的波形如图所示，且()f t 是t 的偶函数，其傅里叶级数只有奇次谐波，画出整个周期内()f t 信号的波形。

4、计算222)(ta at f +=的傅里叶变换()F j ω= 。

2a eωπ-5、图中所示电路的频率响应)(ωj H = 。

RR j Lω+6、理想低通滤波器在物理上是否可以实现？ ，说明理由： 。

不能实现，因为违背了因果律7、画出图中)(t f 的偶分量波形。

8、简述周期信号频谱的特点： 。

离散性、谐波性、收敛性9、已知系统的幅频特性1)(=ωj H ，信号通过该系统是否会失真？ ，理由是 。

不一定失真，该系统相频特性未知，若相频特性是经过原点的直线则不会失真，否则失真。

10、已知理想高通滤波器的系统函数()()00()0 0 j tj Ke H j H j e ωϕωωωωωωω--⎧>⎪==⎨<⎪⎩，则该系统的冲激响应()h t = 。

00000000sin[()]()()[()]()K t t K K t t K t t S t t t t ωωδδαωππ---=----二、 （10分）计算如图所示波形信号)(t f 的频谱函数)(ωj F 。

解： ()()2()()f t t t t ετεετ=+-+- （2分）()'()2()()f t t t t δτδδτ=+-+- （3分）()22cos()24sin()2j j j F j e e ωτωτωτωωωτ-=-+=-=- （3分）()24sin ()2j F j ωτωω=或2cos()2j ωτω-或22()2j S ωττα （2分）三、 （10分）已知1()f t 的频谱函数为121F (),()()j f t f t ω与波形有如图所示的关系，试用1()f t 的频谱函数表示2()f t 的频谱函数)(F 2ωj 。

福师《信号与系统》在线作业二-0006
试卷总分:100 得分:100
一、单选题 (共 25 道试题,共 50 分)
1.在变换域中解差分方程时，首先要对差分方程两端进行( )。

A.拉普拉斯变换
B.傅立叶变换
C.以上答案都不正确
D.Z变换
答案:D
2.信号f(t)与δ(t)的卷积等于( )。

A.δ(t)
B.f(t)δ(t)
C.f(t)
D.0
答案:C
3.在一个周期内绝对可积是周期信号频谱存在的( )条件。

A.必要
B.充要
C.充分
D.以上答案都不正确
答案:A
4.零输入响应是( )。

A.部分零状态响应
B.部分自由响应
C.全部自由响应
D.全响应与强迫响应之差
答案:B
5.信号f(t)=[A+sin(200πt)]cos(2000πt)的归一化功率等于( )。

A.以上答案都不正确
B.A*A/2+1/4
C.A*A/2
D.1/4
答案:B
6.函数f(s)=(s+6)/[(s+2)*(s+5)]逆变换的终值等于( )。

A.6
B.2
C.1
D.0
答案:D。