近交系数的计算

自交的近交系数-概述说明以及解释1.引言1.1 概述概述：自交和近交是遗传学领域中重要的概念，它们指的是在繁殖过程中个体内部或者同一物种之间的亲缘关系。

自交指的是两个亲缘关系极为近的个体进行交配，而近交则是指来自同一亲本或亲缘极近的个体进行交配。

自交和近交在生物学研究中有着重要的意义，它们不仅影响到物种的进化和遗传变异，还会对种群的遗传多样性和适应性产生影响。

通过计算自交和近交系数，我们可以更好地了解遗传背景，优化繁殖计划，预防疾病遗传等方面的工作。

本文将详细介绍自交和近交的概念、影响以及近交系数的计算方法，旨在帮助读者更好地理解这一重要的遗传学概念，以及应用于实际研究和繁殖中的意义。

1.2 文章结构文章结构部分将会包括以下内容：1. 引言：介绍自交和近交系数的概念及其重要性。

2. 正文：- 什么是自交和近交：解释自交和近交的概念，以及它们在生物学和遗传学中的作用。

- 自交的影响：探讨自交对种群遗传多样性和适应性的影响，以及可能导致的遗传缺陷。

- 近交系数的计算方法：介绍近交系数的计算方法和其在遗传学研究中的应用。

3. 结论：总结自交和近交系数的重要性，讨论其在实际应用中的潜力，并展望未来的研究方向。

通过这样的结构，读者可以系统地了解自交和近交系数的相关知识，并进一步探讨其在遗传学和生物学领域的重要性和应用前景。

1.3 目的本文的主要目的是探讨自交的近交系数在遗传学研究中的重要性和应用。

通过分析自交和近交对基因型和表型的影响，我们可以更好地理解遗传变异和遗传相关性。

同时，我们也将介绍近交系数的计算方法，帮助读者更深入地理解自交的影响。

通过本文的阐述，希望能够引起更多研究者对自交和近交系数的关注，促进相关领域的发展和进步。

2.正文2.1 什么是自交和近交:自交和近交是遗传学中的两个重要概念，它们都涉及到生物种群内部的遗传交流。

自交是指同一种群中的个体之间进行交配，而近交则是指亲缘关系较近的个体之间进行交配。

fis近交系数（实用版）目录1.FIS 近交系数的定义2.FIS 近交系数的计算方法3.FIS 近交系数的应用4.FIS 近交系数的局限性正文FIS 近交系数（Federation of Indian Societies consanguinity coefficient）是一种衡量个体之间亲缘关系的指标，主要用于研究印度社会中的近亲婚姻现象。

在印度，近亲婚姻较为普遍，尤其是在某些地区和种姓中，认为近亲婚姻可以维护家族血统的纯净。

然而，这种做法可能导致基因缺陷和遗传疾病的风险增加。

因此，了解和研究 FIS 近交系数具有重要意义。

FIS 近交系数的计算方法是基于概率论和统计学的原理。

具体来说，它通过计算两个个体的基因型概率，来估算他们之间的亲缘关系。

FIS 近交系数的取值范围在 0-1 之间，数值越大表示亲缘关系越近。

当 FIS 近交系数为 1 时，表示两个个体为同卵双胞胎；当 FIS 近交系数为 0 时，表示两个个体没有亲缘关系。

FIS 近交系数在印度社会中有着广泛的应用。

首先，它可以帮助研究者了解印度社会中的近亲婚姻现象，为相关政策的制定提供科学依据。

此外，FIS 近交系数还可以应用于遗传疾病的研究，帮助医生和患者了解疾病的遗传风险，从而采取有效的预防措施。

然而，FIS 近交系数也存在一定的局限性。

首先，它的计算方法基于理想状态下的基因型概率，可能与实际情况存在偏差。

其次，FIS 近交系数只能反映个体之间的亲缘关系，不能完全代表个体的遗传特征。

因此，在实际应用中，需要结合其他遗传学指标和方法，才能更全面地了解个体的遗传信息。

总之，FIS 近交系数作为一种衡量亲缘关系的指标，对于研究印度社会的近亲婚姻现象和遗传疾病具有重要意义。

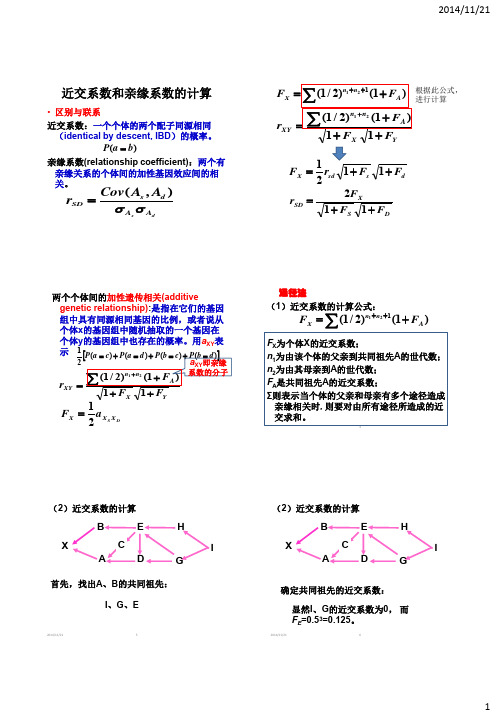
•区别与联系近交系数：一个个体的两个配子同源相同（identical by descent, IBD ）的概率。

亲缘系数(relationship coefficient)：两个有亲缘关系的个体间的加性基因效应间的相关。

近交系数和亲缘系数的计算dsAA d s SDA A Cov r σσ),(=)(b a P =YX A n n XYF F F r +++=∑+11)1()2/1(21∑+=++)1()2/1(121A n n X F F d s sd X F F r F ++=1121DS XSD F F F r ++=112根据此公式，进行计算两个个体间的加性遗传相关(additivegenetic relationship):是指在它们的基因组中具有同源相同基因的比例，或者说从个体x 的基因组中随机抽取的一个基因在个体y 的基因组中也存在的概率。

用a XY 表示 [])()()()(21d b P c b P d a P c a P =+=+=+=YX A n n XYF F F r +++=∑+11)1()2/1(21a XY 即亲缘系数的分子DS X X X a F 21=4（1）近交系数的计算公式：F X 为个体X 的近交系数；n 1为由该个体的父亲到共同祖先A 的世代数； n 2为由其母亲到A 的世代数； F A 是共同祖先A 的近交系数；Σ则表示当个体的父亲和母亲有多个途径造成亲缘相关时, 则要对由所有途径所造成的近交求和。

∑+=++)1()2/1(121A n n X F F 通径法2014/11/21 5（2）近交系数的计算CXBADE HGI首先，找出A 、B 的共同祖先：I 、G 、E2014/11/216（2）近交系数的计算CXB ADE HGI确定共同祖先的近交系数： 显然I 、G 的近交系数为0， 而F E =0.53=0.125。

2014/11/217（2）近交系数的计算CXBADE HGI确定连接A 和B 的通径链:B←E→C→AB←E→D→A B←E←G→D→AB←E←H←I→G→D→A通径链 共同祖先的近交系数n 1+n 2+1通径链的系数 B←E→C→A 4 B←E→D→A 4 B←E←G→D→A F G =0 5 B←E←H←I→G→D→AF I =07F X = 23/1288•最后，将各通径链的系数累加即得X 的近交系数。

近交系数的计算-答案设有下列系谱，试用一般计算公式、共亲系数列表算法以及加性遗传相关算法分别求各个体的近交系数和个体间的亲缘系数。

答：一、近交系数的计算（一）利用近交系数的一般公式计算 1. X 个体（1）父母A 和B 的共同祖先有：C 、D 、F 、H ；它们均为非近交个体(判断一个个体是否为近交个体的依据是看其父母是否有共同祖先，如果双亲只知道一方或均未知则默认其为非近交个体)，因此，F C =0，F D =0，F F =0，F H =0。

（2）找通径链，并计算各通径链的系数，求和计算出F X 通径链共同祖先的近交系数n 1+n 2+1 通径链的系数 A ←C →B A ←D →B A ←C ←F →D →B A ←D ←F →C →B A ←C ←E ←H →G →D →B A ←D ←G ←H →E →C →B F C =0 F D =0 F F =0 F F =0 F H =0 F H =03 3 5 5 7 7F X = 21/642. A 个体（1）父母C 和D 的共同祖先有F 和H ，且F F =0，F H =0。

（2）找通径链，并计算各通径链的系数，求和计算出F A 。

321)(321)(521)(521)(721)(721)(通径链 共同祖先的近交系数 n 1+n 2+1 通径链的系数 C ←F →D A ←E ←F →G →DF F =0 F H =03 5F A = 5/323.B 个体，与A 个体同父同母，因此与A 相同。

F B = 5/32。

4.其余个体C 、D 、E 、F 、G 、H 均为非近交个体，F C =0，F D =0，F E =0，F F =0，F G =0，F H =0。

（二）利用加性遗传相关列表算法1. 将系谱中的个体按照世代从高到低分别从左到右、从上到下排列，并将个体的双亲编号列于个体的上方。

2. 利用公式计算两两个体间的加性遗传相关，并列表。

其中，x 、y 分别表示任意一个个体；x s 、x d 分别表示x 个体的父亲和母亲；y s 、y d 分别表示y 个体的父亲和母亲。

近交系数——形成合子的两个配子来自同一共同祖先的概率。

根据通径系数原理，个体x 的近交系数即是形成x 个体的两个配子间的相关系数，用F x 表示。

1211(1)2n n x A F F ++⎡⎤⎛⎫=+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦
∑ 式中，x F 表示个体x 的近交系数；1/2 表示各代遗传结构的半数；
1n 表示父亲到共同祖先的代数；2n 表示母亲到共同祖先的代数；
A F 表示共同祖先自身的近交系数；121n n N ++=为亲本相关通径链中的个体数。

第一代全同胞后代的近交系数应该是：
这样亲本相关通径链为：
S---A---D N=3
S-----C----D N=3
1111111125%22x F ++++⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭
即：（1/2）3×2=1/4=25%
连续二代全同胞交配后代的近交系数应该是：
A B F
X
C E G
X 个体就是连续三代全同胞交配产生的后代。

第一步：寻找共同祖先B 、E 、F 、G
F F ＝F
G =F B ＝F E =0
第二步：寻找通径
共同祖先为B 时：A ←B →C N=2
共同祖先为E 时：A ←E →C N=2
共同祖先为F 时：A ←B ←F →E →C N=4
C←B←F→E→A N=4
供同祖先为G时：A←B←G→E→C N=4
C←B←G→E→A N=4
第二步：计算
F X=1/24+1(1+0)×2+1/24+1(1+0)×2+1/22+1(1+0) +1/22+1(1+0) = 3/8=0.375以此类推。

遗传学之八----近亲繁殖系数的简单计算虽然有电脑程式可以应用，只需将照血统书的名字输入数据库，便可以自动计算近亲繁殖系数，但是如果血统书的近亲繁殖比较简单的时候，人手计算也是非常方便。

现在简短的介绍如何利用路径系数path coefficient方法计算近亲繁殖系数。

路径系数方法首先绘画一个“箭头血统书”，在这一个图中每一个体都只出现一次。

箭头从父母指向后代，箭头只可以向下或对角向下。

例1例1：原本的血统书和箭头血统书。

在箭头血统书中，我们找出所有从父母中的一只指向另一只后代，而中间经过其他的猫，而个别的猫不能在路径中出现超过一次。

每一条路径，我们计算有多少猫涉及的数目。

每一条路径对近亲繁殖系数的影响是1/2再以路径中出现的个体数目为次方。

从例1的箭头血统书，我们从每一只父母得出两条路径到达其他的猫：CAD->(1/2)³=1/(2 x 2 x 2)=1/8CBD->(1/2)³=1/(2 x 2 x 2)=1/8近亲繁殖=1/8+1/8=1/4=0.25=25%如果有共同祖先，即：路径折转并再重新向下，我们要考虑是同系繁殖。

（在以上的例子中，两条路径的共同祖先，分别是A和B都被画上了下划线。

）利用路径系数方法计算同系繁殖共同祖先的近亲繁殖系数。

1加共同祖先乘以近亲繁殖系数，再次方在路径上涉及的猫的数目。

因此，如果在这一条路径上出现的个体猫的总数为n，而近亲繁殖系数的共同祖先是F，涉及近亲繁殖系数将会是(1/2)^nx(1+F)。

所有路径的涉及近亲繁殖系数的总和便是近亲繁殖系数。

例2例2:原本的血统书和箭头血统书。

现有的路径是：BDC、BDFEC、BEFDC、BDEC、B EDC、BEC。

共同祖先是D是近交，而他的箭头血统书将会是如此：D的箭头血统书D的近亲繁殖是(1/2)²=1/4。

每一条路径的涉及近亲繁殖系数将会是：Path n F (1/2)^n x(1+F) total BDC 3 1/4 (1/2)³x(1+1/4)=1/8 x 5/4=5/32 =0.15625 BDFEC 5 0 (1/2)^5 x(1+0)=1/32 =0.03125 BEFDC 5 0 (1/2)^5 x(1+0)=1/32 =0.03125 BDEC 4 0 (1/2)^4 x(1+0)=1/16 =0.0625 BEDC 4 0 (1/2)^4 x(1+0)=1/16 =0.0625 BEC 3 0 (1/2)³x(1+0)=1/8 =0.125 近亲繁殖=涉及总和=0.46875=46.875%。