衍射极限
- 格式:doc
- 大小:2.08 MB
- 文档页数:6

光学成像中的衍射极限分析在光学成像领域,衍射极限是一个非常重要的概念。
它用于描述成像系统的分辨能力,即成像系统能够分辨的最小空间尺度。
在本文中,我们将会详细地探讨衍射极限的相关概念和计算方法。
1. 衍射现象的基本概念在介绍衍射极限之前,我们需要先了解几个基本概念。
衍射是指光线遇到一个不规则的物体或一个缝隙后,沿着新的方向传播并产生干涉和衍射现象的现象。
它是光学中的一种基本现象,常见的例子包括照在CD或DVD上的激光束折射现象、棱镜折射和光的散射等。
在衍射现象中,出射光波的振幅和相位都被影响,而且这些影响是由遇到物体或缝隙的孔径大小和光的波长决定的。
因此,当光波遇到一个孔径大小为d的孔时,出射光波的振幅和相位会发生变化。
衍射现象所观察到的光强度模式,即所谓“衍射图样”,取决于这些波的相对相位差。
衍射现象是理解成像系统行为的基础。
在形成图像时,光线穿过物体或物体的表面散射,然后到达成像系统的入射面,最终被聚焦到技术传感器或目镜中。
衍射会改变光线的传播方向,从而影响成像系统对物体细节的分辨能力。
2. 衍射极限的定义衍射极限是指光学成像系统在特定条件下能够分辨的最小空间尺度。
它取决于光的波长和孔径大小,具体计算可以通过Abbe理论或Rayleigh判据实现。
例如,在任意成像条件下,使用激光器或白光成像系统,衍射极限可以计算为:D = 1.22λ / NA其中,λ是光的波长,NA表示成像系统的数值孔径,D是衍射极限的直径。
这个公式称为Abbe限制,它表明高分辨率成像需要使用较小的数值孔径和短波长的光源。
衍射极限是光学成像中一个非常重要的概念,它对成像系统的分辨能力和成像质量都有很大影响。
当试图分辨比衍射极限更小的物体时,我们就会看到衍射现象和方差或所谓的模糊度。
因此,在进行高质量成像时,我们需要选择适当的成像系统参数(例如光源、数值孔径等)以确保系统能够达到最优的成像质量。
3. 衍射极限的计算方法计算衍射极限需要考虑成像系统的各种参数,例如,光源的波长、数值孔径和物体到镜头的距离等。

阿贝衍射极限
阿贝衍射极限是一种新兴的量子效应,它可以实现电子系统中精确定向传输信息,在增强快速传输数据和精确定向传感领域有重要的应用。
阿贝衍射极限也称为量子衍射,是指当光通过一个只有很小细分度的结构时,
会发生极小的量子波动,这就是衍射极限。
这种现象对快速数据传输有着重要的意义,比如可以将一定量的信息在短时间内准确传输到期望的目标地点。
同时,阿贝衍射极限能够实现极具穿透性的信息传输,在定位、检测和控制方面有重要应用。
阿贝衍射极限也有重要的工业应用。
它能够有效减少传统方式定位和检测的时间,提高工作质量。
一般而言,采用衍射极限的方式会提高定位和检测的精度和准确性。
在高精度检测任务中,比如航空航天领域,它可以使传感器精度提高几个数量级。
总之,阿贝衍射极限在快速传输信息,精确定位和控制以及极具穿透性信息传
输等方面有着广泛的应用。
阿贝衍射极限是当今传输技术领域发展的一个重要趋势,在未来应用也前景广阔。

阿贝衍射极限和瑞利判据
阿贝衍射极限和瑞利判据是光学中用于描述光的衍射现象的两个重要概念。
阿贝衍射极限是指像的最小分辨角度,也即光学系统能够分辨出两个点光源的最小夹角。
在阿贝衍射极限以下,两个点光源的像在观察者的视野中会重叠在一起,无法分辨。
而当两个点光源的夹角超过阿贝衍射极限时,观察者能够分辨出两个点光源的像。
阿贝衍射极限与光学系统的孔径大小有关,孔径越大,阿贝衍射极限越小,像的分辨能力越好。
瑞利判据是用于描述光的衍射现象的另一个重要概念,它与光的波长和孔径的大小有关。
瑞利判据定义了一个能够判定两个光源是否能够被光学系统分辨的准则。
根据瑞利判据,如果两个光源的距离小于等于瑞利判据,则它们无法被光学系统分辨,其像会叠加在一起。
而当两个光源的距离大于瑞利判据时,它们能够被光学系统分辨开,其像不会重叠。
综上所述,阿贝衍射极限描述了光学系统能够分辨出两个点光源的最小夹角,而瑞利判据描述了光学系统能够分辨出两个点光源的最小距离。
这两个概念都与光的波长、光学系统的孔径大小以及观察者的视力有关。


衍射极限艾里斑分辨率-概述说明以及解释1.引言1.1 概述在概述部分,我们将介绍衍射极限艾里斑分辨率这一主题的背景和重要性。
衍射极限艾里斑分辨率是一种用于评估和描述光学系统分辨能力的指标。
光学系统的分辨能力是指其能够将空间中两个点状物体分辨为两个离散的点的能力。
衍射极限艾里斑分辨率的概念源于19世纪的衍射理论和光的波动性质。
根据衍射理论,当光束通过一个孔径较小的光学系统时,光的波动会导致光斑的扩散和干涉现象,从而限制了系统的分辨能力。
艾里斑分辨率是一种经典的衡量光学系统分辨能力的方法。
它是由物理学家Ernst Abbe于1873年提出的,并以他的名字命名。
艾里斑分辨率的计算基于光学系统的参数,包括光的波长和系统的数值孔径。
衍射极限艾里斑分辨率在科学研究和实际应用中具有重要意义。
在生物医学领域,它可以用于评估显微镜的分辨能力,进而实现对细胞和组织结构的高分辨率成像。
在光刻技术中,艾里斑分辨率的理论极限可以指导光刻机的设计和性能改进。
然而,衍射极限艾里斑分辨率也存在一定的局限性。
实际光学系统往往受到各种因素的限制,如光的衍射、散射、畸变等,这些因素会降低系统的实际分辨能力。
因此,进一步研究和改进光学系统,以提高其分辨能力成为未来发展的方向。
在接下来的文章中,我们将详细介绍衍射极限的定义和原理,以及艾里斑分辨率的概念和计算方法。
我们还将讨论衍射极限艾里斑分辨率在不同领域的应用,并探讨其存在的局限性和未来的发展方向。
通过对这一主题的全面了解,我们可以更好地理解光学系统的分辨能力,并为相关领域的进一步研究和应用提供指导。
1.2文章结构文章结构部分的内容可以是对整篇文章的组织和布局进行介绍。
可以提及文章的各个章节主题、内容概要以及各个章节之间的逻辑关系等。
以下是关于文章结构部分的一个示例:第2节正文部分是本文的核心内容,将详细介绍衍射极限和艾里斑分辨率的定义、原理和计算方法。
通过对衍射极限的研究和艾里斑分辨率的计算,我们可以更好地理解光学成像中的分辨率限制和相关原理。

ZEMAX中的调制传递函数MTF衍射极限是如何计算的在ZEMAX软件中,调制传递函数(Modulation Transfer Function,MTF)用于描述光学系统的成像能力。
MTF衍射极限是指在理想情况下,光学系统能够达到的最高分辨率。
下面将对ZEMAX中MTF衍射极限的计算过程进行详细说明。
MTF是通过计算系统的点扩散函数(PSF)来获得的。
点扩散函数是描述光学系统对无穷小点光源成像的结果。
可以通过ZEMAX的“Analysis”菜单下的“MTF/PSF”选项来计算系统的MTF衍射极限。
首先,在ZEMAX中,需要创建一个模型来表示光学系统。
这可以通过使用适当的元件来构建光学系统的光学路径,例如镜头、透镜、棱镜等。
可以利用ZEMAX中提供的库中的元件或者自行定义元件。
接下来,需要在光学系统中定义一个理想的点光源。
这可以通过在“Analysis”菜单下选择“Wavefront”选项,然后选择“Rays…”来定义。
在光源定义中,可以选择光线的起始点和方向,以及光线的光谱分布。
一旦完成光学系统和点光源的定义,就可以进行MTF计算。
在“Analysis”菜单下选择“MTF/PSF”选项。
在MTF/PSF设置窗口中,可以选择计算MTF所需的一些参数,如采样点数量、采样频率等。
可以根据需要来选择这些参数。
计算完成后,ZEMAX将显示MTF结果。
理想情况下,MTF曲线应该是水平的,在频率为零处为1,表示系统能够完美地传输所有的频率成分。
然而,实际情况下,由于各种因素的限制,光学系统的MTF曲线会出现衰减。
MTF衍射极限是MTF曲线在频率等于系统的Nyquist频率处的值。
综上所述,ZEMAX中MTF衍射极限的计算是通过计算系统的点扩散函数来实现的。
可以通过定义光学系统、光源和选择计算参数来进行MTF计算。
计算结果可以用于评估光学系统的分辨能力,并进行系统设计和优化。

光学衍射极限分辨率光学衍射极限分辨率是指在使用光学显微镜对物质进行观察时,能够获得的最小可分辨的两个物体之间的距离。
这个距离取决于光学系统的特性和观察条件。
这个极限分辨率是由物理学定律决定的,在任何光学显微镜系统中都是存在的。
光学衍射极限分辨率是受到物理学上的瑞利判据的限制的。
瑞利判据是一个经典的物理学经验法则,它规定两个靠近的物体之间的距离必须大于或等于波长的一半才能够被分辨出来。
如果物体的间距小于波长的一半,就无法在显微镜中被分辨出来。
这就是所谓的瑞利极限。
瑞利极限是由于光的本性所决定的。
光是一种波动性质的粒子,当它遇到物体时,就会发生衍射。
衍射是指光波从物体表面经过变化后继续传播的过程。
这种变化包括光的折射、反射和透过。
当光波经过物体的表面时,它会发生散射和干涉,这就导致了衍射现象。
衍射是光学显微镜工作的基础。
当物体的间距小于瑞利极限时,它们就会被认为是一个整体,因为光波无法分辨它们的不同。
在显微镜中,光线传递到物体表面时会经过透镜,透镜会将光线聚焦在一个点上。
在这个点上,光波将受到物体表面的反射和散射,这导致光波从点上扩散出去。
如果两个物体的间距太小,就无法分辨出它们的光波扩散所形成的图像。
因此,光学衍射极限分辨率是在光学显微镜中观察物体时最小的可分辨两个物体的距离。
它受到光的波长、透镜的特性、光的入射角度和物体的性质等很多因素的影响。
为了获得更高的分辨率,可以采用高波长的光、高质量的镜头、更精确的调焦系统以及更强的光源等方法,但这些方法都有其限度。
总之,光学衍射极限分辨率是光学显微镜能够分辨两个相邻物体之间的最小距离。
它受到多种因素的影响,为了获得更高的分辨率,需要通过各种方法来优化光学显微镜系统。
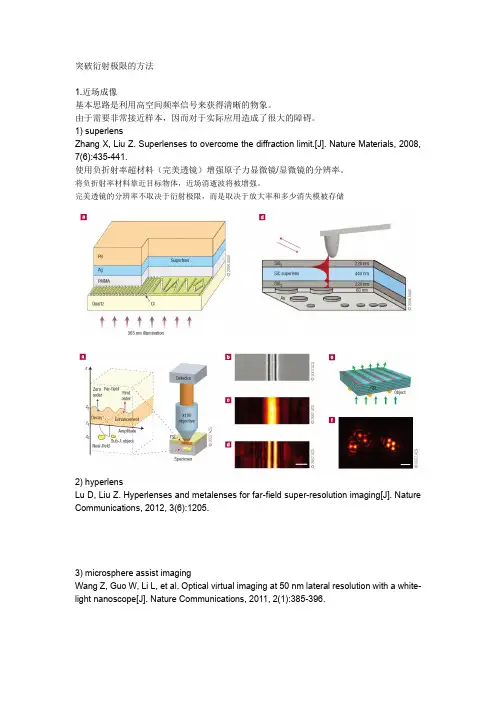
突破衍射极限的方法1.近场成像基本思路是利用高空间频率信号来获得清晰的物象。
由于需要非常接近样本,因而对于实际应用造成了很大的障碍。
1) superlensZhang X, Liu Z. Superlenses to overcome the diffraction limit.[J]. Nature Materials, 2008, 7(6):435-441.使用负折射率超材料(完美透镜)增强原子力显微镜/显微镜的分辨率。
将负折射率材料靠近目标物体,近场消逝波将被增强。
完美透镜的分辨率不取决于衍射极限,而是取决于放大率和多少消失模被存储2) hyperlensLu D, Liu Z. Hyperlenses and metalenses for far-field super-resolution imaging[J]. Nature Communications, 2012, 3(6):1205.3) microsphere assist imagingWang Z, Guo W, Li L, et al. Optical virtual imaging at 50 nm lateral resolution with a white-light nanoscope[J]. Nature Communications, 2011, 2(1):385-396.4) nearfield scanning optical microscopy2.远场成像可以做到远场高分辨,达到几十纳米的分辨率,通过选择性激活或者灭活荧光团但是这些成像技术仅适用于生物组织样本1)STEDStimulated emission depletion microscopy受激发射减损显微镜https:///wiki/STED_microscopy2) PALMphoto-activated localization microscopy光激活定位显微镜https:///wiki/Photoactivated_localization_microscopy3) STORM随机光学重构显微技术Stochastic optical reconstruction microscopyhttps:///wiki/Super-resolution_microscopy#Stochastic_optical_reconstruct ion_microscopy_.28STORM.293.SOLsuper-oscillatory lens超震荡透镜Berry M V. Exact nonparaxial transmission of subwavelength detail using superoscillations[J]. Journal of Physics A Mathematical & Theoretical, 2013,46(20):2140-2154.。

衍射极限艾里斑分辨率全文共四篇示例,供读者参考第一篇示例:衍射极限艾里斑分辨率(Diffraction-limited resolution)是光学成像领域一个非常重要的概念,它代表着在理论最佳条件下,光学系统能够实现的最小分辨距离。
衍射极限艾里斑分辨率是由法国物理学家艾里斑(Joseph von Fraunhofer)提出的,他通过研究光线在开放孔径中衍射的现象,得出了衍射极限分辨率与波长和孔径大小之间的关系。
光学成像系统在进行成像时会受到衍射的影响,即光线通过光圈或孔径时会发生衍射现象,从而导致成像细节的模糊。
根据艾里斑理论,光学系统的分辨率受到波长和孔径大小的限制,即分辨率越高,波长越短,孔径越大。
当达到衍射极限艾里斑分辨率时,光学系统将不再能够准确分辨出比这个距离更小的物体细节。
在实际应用中,衍射极限艾里斑分辨率是光学系统设计和优化的重要参考依据之一。
通过精心设计光学系统的波长和孔径,可以有效提高系统的分辨率,从而获得更加清晰和精准的成像效果。
衍射极限艾里斑分辨率也在生物医学成像、天文观测等领域发挥着重要作用,帮助科研人员更好地观测和研究微小物体的结构和性质。
除了光学系统设计外,人们还通过其他优化手段来突破衍射极限艾里斑分辨率,例如超分辨成像技术。
超分辨成像技术是近年来兴起的一项前沿技术,它通过特殊的成像算法或设备,能够实现超越传统衍射极限分辨率的成像效果,提高成像的清晰度和准确度。
这种技术的出现为光学成像领域带来了革命性的变革,推动了科学研究和工程应用的进步。
在未来,随着科技的不断进步和创新,人们对于衍射极限艾里斑分辨率的研究将继续深入,优化光学系统的设计和应用,推动超分辨成像技术的发展,拓展成像领域的边界。
衍射极限艾里斑分辨率作为光学成像领域的基础理论之一,将继续发挥着重要的作用,为科学研究和工程应用提供可靠的支持。
衍射极限艾里斑分辨率是光学成像领域的重要概念之一,它代表着光学系统在最佳条件下能够实现的最小分辨距离。

菲涅尔变换极限菲涅尔变换极限是光学领域中的一个重要概念,它在光的衍射和干涉现象中起着至关重要的作用。
本文将详细介绍菲涅尔变换极限的概念、原理及其在光学中的应用。
菲涅尔变换极限,又称为菲涅尔衍射极限或菲涅尔近似,指的是当光波的传播距离远大于光的波长时,可以近似将光波的传播过程看作是平面波的传播。
这一近似在光学中的应用非常广泛,尤其在衍射和干涉现象的研究中被广泛使用。
在光的衍射现象中,菲涅尔变换极限的应用可以简化计算过程,使其更加便捷。
衍射现象是光波通过一个障碍物或通过两个或多个障碍物之间的间隙时产生的波的干涉效应。
以单缝衍射为例,当光波通过一个很窄的缝隙时,缝隙的宽度和光的波长之间的比值决定了衍射角的大小。
当缝隙的宽度很小时,可以近似认为光波是平面波,这时就可以应用菲涅尔变换极限进行计算。
通过计算可以得到衍射图样的强度分布和衍射角的大小。
在光的干涉现象中,菲涅尔变换极限的应用同样非常重要。
干涉现象是指两个或多个光波相遇时产生的波的叠加效应。
以杨氏双缝干涉为例,当两个狭缝中的光波相遇时,会在干涉屏上形成一系列明暗相间的条纹。
通过应用菲涅尔变换极限,可以得到干涉图样的强度分布和干涉条纹的间距。
菲涅尔变换极限的应用不仅限于衍射和干涉现象,还可以在光学成像、光学信息处理等领域中发挥重要作用。
在光学成像中,菲涅尔变换极限可以用来分析和优化光学系统的成像效果,帮助提高图像的清晰度和分辨率。
在光学信息处理中,菲涅尔变换极限可以用来实现光学信号的调制、解调和编码等功能,为光学通信和光学计算提供支持。
菲涅尔变换极限是光学领域中的一个重要概念,它在衍射、干涉、光学成像和光学信息处理等方面都有广泛的应用。
通过应用菲涅尔变换极限,可以简化计算过程,提高效率,并且可以更好地理解和解释光学现象。
因此,在光学研究和应用中,菲涅尔变换极限的理论和方法具有重要的意义。

衍射极限储存环光源
衍射极限储存环光源是近年来科技领域中的一项重大突破,它可
以有效解决光源强度不足的问题。
在本文中,我们将会分步骤详细阐
述衍射极限储存环光源的原理,以及它的应用及未来发展方向。
第一步:原理
衍射极限储存环光源最初是由日本科学家三吉彩乃提出的。
它的
原理基于光子在光学晶体中的衍射现象,通过光子与光学晶体相互作
用而形成光束。
晶体的周期性结构可以将光束在晶体的一定区域内聚焦,从而增强光源的强度。
第二步:应用
衍射极限储存环光源在光学领域有广泛的应用,其中最为典型的
应用是在光刻机上。
光刻机是半导体行业中非常重要的一种设备,它
主要用来将电路图案转移到硅片上。
衍射极限储存环光源可以在光刻
机中扮演非常重要的角色,因为它可以提高光刻机的加工精度,从而
影响半导体芯片的性能和功耗。
第三步:未来发展方向
目前,衍射极限储存环光源的性能仍有待进一步提高。
在未来的
研究中,科学家们将会发掘更多的光学晶体,并基于这些晶体的特性
来研究新的光源。
此外,在研究过程中,科学家们还将结合人工智能、机器学习和深度学习等前沿技术来提高光源的性能和稳定性。
综上所述,衍射极限储存环光源不仅可以有效解决光源强度不足
的问题,而且它在光学领域中有着非常广泛的应用。
虽然它还有很多
不足之处,但是随着科学技术的不断发展,相信未来的衍射极限储存
环光源将会有着更加广阔的发展前景。
衍射极限是指一个理想点物经光学系统成像,由于衍射的限制,不可能得到理想像点,而是得到一个夫朗和费衍射像。
因为一般光学系统的口径都是圆形,夫朗和费衍射像就是所谓的艾里斑。
这样每个物点的像就是一个弥散斑,两个弥散斑靠近后就不好区分,这样就限制了系统的分辨率,这个斑越大,分辨率越低。
这个限制是物理光学的限制,是光的衍射造成的。
这种衍射限制本质上来源于量子力学中的测不准关系限制。
对于给定频率的光子,当它在某个方向上的动量范围给定时,它的分辨率也就定了。
一般当一个艾里斑的中心和另一个艾里斑的边缘暗环刚好重合时,认为两个像斑刚好能够分辨(瑞利判据)。
这一现象用傅立叶分析理论可解释为:携带物体信息的入射光波的傅立叶分量中,较大的横向分量对应着高频成分,代表着物体的细节部分;但含高频横向分量的光波因满足2222x y k k w c +〉 (k x 、k y 为波矢量K 在x和y 方向分量,ω为光波角频率、c 为光速,传播方向为z 轴)而成为倏逝波,倏逝波在传播过程中因振幅呈指数衰减而无法到达像面,不能参与成像,造成物体细节部分的丢失,因而普通透镜的成像总是有缺陷的。
图1. 艾里斑图形(三维强度值和和平面图像)衍射极限公式是sinθ=1.22λ/D 。
其中θ是角分辨率,λ是波长,D 是光圈直径。
当θ很小时,sinθ约等于tanθ,约等于d/f ,其中d 是最小分辨尺寸,f 是焦距。
推导出d/f=1.22λ/D 。
显微镜的可分辨的最小线度为:δy=0.61λ/N.A.,其中N.A.为镜头的数值孔径。
目前,普通显微镜的分辨率一般为200nm 以上。
突破衍射极限:在物理概念上从只使用实数推广到使用虚数;从物理上讲,属于从传统中那样使用实光子辐射场推广到使用非辐射的虚光子场(不在光子质壳上的光子都是虚光子),前者就是传统中的光学成像,后者则属于近场成像。
产生电磁波的源都可以称为天线。
天线产生辐射远场和非辐射近场,前者包括我们通常看到的一束光,它在真空中传播,幅度不会衰减;后者则随空间距离迅速衰减,主要局域于天线附近,属于局域性的电磁波,或者附在材料表面附近的“表面波”。
声波衍射极限
声波衍射是一种广泛用于声学和物理学领域的技术。
它可以用于确定物体的形状、尺寸和位置,以及分析材料的结构和性质。
声波衍射的原理是在物体周围形成一个声波场,它与物体相互作用并产生衍射现象。
声波衍射极限是指在给定条件下,可以获得的最小物体特征的大小。
这个极限取决于声波的频率、波长、传播距离、探测器的分辨率和材料的特性等因素。
通过改善声波源、探测器和信号处理技术,可以提高声波衍射的分辨率和灵敏度,从而获得更高的声波衍射极限。
- 1 -。
光学显微镜分辨率衍射极限光学显微镜分辨率衍射极限光学显微镜是一种基础科研和应用研究领域中不可或缺的工具。
在过去的几个世纪中,它被广泛应用于生物学、物理学、医学和材料科学等领域。
但是,光学显微镜的分辨率衍射极限成为了限制其应用范围的重要因素,所以在深入研究光学显微镜时,分辨率衍射极限是非常重要的一个概念。
分辨率的定义是指一台显微镜可以观察到最小物体的尺寸。
在光学显微镜中,分辨率衍射极限是由衍射现象来限制的。
衍射是光子通过物体表面时发生的散射现象,其直接影响了最终的图像质量和分辨率。
在光学显微镜中,一个物体的细节可以通过光波的折射传输到目镜中。
然而,当一个物体的大小小于波长时,光学显微镜的分辨率就会受到极限的制约。
这个极限被称为光学显微镜的分辨率衍射极限。
分辨率衍射极限的大小与波长有关。
在可见光波段中,绿色光的波长为550 nm左右,因此绿光的分辨率衍射极限约为200 nm。
虽然这个分辨率对于大多数生物学和物理学实验已经足够,但是在最高分辨率的应用中,它还是显得比较低。
虽然分辨率衍射极限是一个固定的值,但是有许多方法可以提高分辨率。
其中最为常见的方法是所谓的超分辨率显微镜。
这些显微镜在光学显微镜的基础上增加了高级光学元件,例如可变焦镜头、荧光定位显微镜技术、光学声学成像技术等等,以提高光学显微镜的分辨率衍射极限。
总之,分辨率衍射极限是光学显微镜中最基本的概念之一。
光学显微镜是许多领域中不可或缺的工具,但由于分辨率衍射极限的存在,其应用受到了严格的限制。
然而,随着超分辨率显微镜技术的不断发展,光学显微镜的应用范围也在不断地拓展。
瑞利衍射极限分辨率
瑞利衍射极限分辨率是指在光学显微镜条件下,两个紧挨着的点能够被分辨的最小距离,也被称为衍射极限或瑞利极限。
它是由英国科学家瑞利在19世纪末提出的,并且被广泛用于显微镜图像的分辨率计算,尤其是用于生物学和医学领域中的细胞和微观结构的成像。
瑞利衍射极限分辨率的计算公式是:分辨率= 0.61×λ/NA,其中λ是入射光线的波长,NA是数值孔径。
从公式中可以看出,分辨率与波长和数值孔径有关。
波长越短,分辨率越高,数值孔径越大,分辨率也越高。
在显微镜中,光线穿过物体并进入物镜,然后通过透镜聚焦,使得图像被放大并投影到目镜中。
物镜的数值孔径决定了光线聚焦的程度和收集的角度,从而影响了分辨率。
当两个点的距离小于瑞利衍射极限时,它们就不能被分辨出来,从而产生重叠的图像,使得细节丧失。
在生物学和医学领域中,瑞利衍射极限分辨率对于显微镜成像非常关键。
如果分辨率太低,就难以看到微小的细胞结构,从而难以进行精确的诊断和研究。
为了提高分辨率,科学家们一直在尝试各种技术和方法,例如使用高数值孔径物镜、加强荧光信号和使用超分辨显微镜等。
总之,瑞利衍射极限分辨率是显微镜成像中重要的概念,它决定了图像可分辨性的上限。
对于生物学和医学研究,了解和掌握分辨率的概念和计算方法是至关重要的。
mtf计算衍射极限衍射极限是指在特定条件下物体能够被观察到的最小细节尺寸。
在光学领域中,衍射极限是指通过光学系统所能够分辨的最小细节尺寸。
这个极限是由光的波动性决定的,即光线通过一个孔径或物体边缘时会发生衍射现象,从而限制了光学系统的分辨能力。
MTF(Modulation Transfer Function)是一种用来描述光学系统传递细节信息的指标。
它是一种频率域的函数,表示不同空间频率下传递的光强比例。
通过测量和计算MTF,我们可以得到光学系统在不同空间频率下的传递特性,从而了解系统的分辨能力。
MTF计算衍射极限的基本原理是利用MTF曲线的截止频率来估算衍射极限。
截止频率是指MTF曲线下降到一定比例(通常为0.1)时对应的空间频率。
在这个频率以下,MTF曲线下降较为陡峭,表示系统无法分辨更高的空间频率,即达到了衍射极限。
因此,通过测量系统的MTF曲线并找到其截止频率,我们可以估算出系统的衍射极限。
MTF计算衍射极限的步骤如下:1. 测量MTF曲线:使用特定的测试图像,通过测量不同空间频率下的光强变化,得到系统的MTF曲线。
这一步通常需要使用专业的测试设备和软件来完成。
2. 分析MTF曲线:根据测量得到的MTF曲线,找到曲线下降到0.1的位置,得到对应的空间频率。
这个频率即为系统的截止频率。
3. 计算衍射极限:根据截止频率,可以通过公式计算出系统的衍射极限。
衍射极限等于光的波长除以两倍的截止频率。
MTF计算衍射极限的方法可以帮助光学工程师评估和优化光学系统的分辨能力。
通过了解系统的衍射极限,可以判断系统是否满足需求,或者在设计过程中进行调整和改进。
此外,MTF计算衍射极限的方法还可以用于比较不同光学系统的性能,选择最合适的系统。
总结起来,衍射极限是光学系统能够分辨的最小细节尺寸,而MTF 是一种用来描述光学系统传递细节信息的指标。
通过测量MTF曲线并计算截止频率,可以估算出系统的衍射极限。
MTF计算衍射极限的方法对于光学系统的评估和优化具有重要意义,可以帮助工程师提高系统的分辨能力和性能。
无透镜系统的衍射极限
无透镜系统指的是没有透镜的光学系统,其可以通过类似于光波束整形器的方法来控制光线的传播和聚焦。
然而,由于物理学中的衍射效应,无透镜系统的聚焦能力会受到限制。
衍射是光线遇到物体边缘或孔隙时发生的现象,导致光线在传播过程中发生弯曲和散射。
对于无透镜系统而言,衍射效应会使得光线的聚焦变得模糊。
而且,由于所有的光线都会发生衍射,因此无透镜系统的聚焦效果会受到极限制。
无透镜系统的衍射极限可以通过衍射限制公式来计算。
该公式可以用来确定光线穿过孔隙的最小尺寸,以及光线在聚焦时的最小点阵距离。
理论上,通过优化无透镜系统的结构和参数,可以尽可能地逼近衍射极限,提高系统的聚焦能力。
在实际应用中,无透镜系统通常用于微型光学元件的设计和制造。
其具有体积小、重量轻、成本低等优点,并且可以与其他微型器件集成在一起,实现多功能的光学系统。
随着纳米技术的发展,无透镜系统的应用前景将会更加广阔。
- 1 -。
衍射极限是指一个理想点物经光学系统成像,由于衍射的限制,不可能得到理想像点,而是得到一个夫朗和费衍射像。
因为一般光学系统的口径都是圆形,夫朗和费衍射像就是所谓的艾里斑。
这样每个物点的像就是一个弥散斑,两个弥散斑靠近后就不好区分,这样就限制了系统的分辨率,这个斑越大,分辨率越低。
这个限制是物理光学的限制,是光的衍射造成的。
这种衍射限制本质上来源于量子力学中的测不准关系限制。
对于给定频率的光子,当它在某个方向上的动量范围给定时,它的分辨率也就定了。
一般当一个艾里斑的中心和另一个艾里斑的边缘暗环刚好重合时,认为两个像斑刚好能够分辨(瑞利判据)。
这一现象用傅立叶分析理论可解释为:携带物体信息的入射光波的傅立叶分量中,较大的横向分量对应着高频成分,代表着物体的细
节部分;但含高频横向分量的光波因满足2222x y k k w c +〉 (k x 、k y 为波矢量K 在x
和y 方向分量,ω为光波角频率、c 为光速,传播方向为z 轴)而成为倏逝波,倏逝波在传播过程中因振幅呈指数衰减而无法到达像面,不能参与成像,造成物体细节部分的丢失,因而普通透镜的成像总是有缺陷的。
图1. 艾里斑图形(三维强度值和和平面图像)
衍射极限公式是sinθ=1.22λ/D 。
其中θ是角分辨率,λ是波长,D 是光圈直径。
当θ很小时,sinθ约等于tanθ,约等于d/f ,其中d 是最小分辨尺寸,f 是焦距。
推导出d/f=1.22λ/D 。
显微镜的可分辨的最小线度为:δy=0.61λ/N.A.,其中N.A.为镜头的数值孔径。
目前,普通显微镜的分辨率一般为200nm 以上。
突破衍射极限:
在物理概念上从只使用实数推广到使用虚数;从物理上讲,属于从传统中那样使用实光子辐射场推广到使用非辐射的虚光子场(不在光子质壳上的光子都是虚光子),前者就是传统中的光学成像,后者则属于近场成像。
产生电磁波的源都可以称为天线。
天线产生辐射远场和非辐射近场,前者包括我们通常看到的一束光,它在真空中传播,幅度不会衰减;后者则随空间距离迅速衰减,主要局域于天线附近,属于局域性的电磁波,或者附在材料表面附近的“表面波”。
事实上,任何材料表面附近(包括金属表面)都存在这种近场,远看是呈电中性,近看则存在电荷密度涨落。
近场有材料内部自己产生的,也有通过外来光波照射材料产生的。
现在来说明一下倏逝场如何可以突破衍射极限,实现光子的空间局域的:对于给定频率ω的光子,光子在某个方向的动量分量K通常小于或等于这个频率ω,根据测不准原理,光子在这个方向上的位置不确定度不小于1/ω(Planck常数置为1),显然频率越高,位置不确定度越小,以这样的光子作为光学显微镜的工作光子时,分辨率将由这个位置不确定度所限制。
这就是传统光学显微镜的分辨率极限。
然而,如果把倏逝近场作为光学显微镜的工作光子,倏逝近场的光子某方向上的动量分量K可以大于光子频率ω,使得光子在这个方向上的位置不确定度可以小于1/ω:1/K <1/ω,从而可以成百上千倍地提高分辨率。
近场光学显微镜比电子显微镜的好处在于,前者对被观察物理不产生损害,而且对被观察对象没有要求,而电子显微镜要求被观察物理物体具有导电性,还要求高真空等等。
1/K<1/ω意味着光子的整个波数矢量(或动量矢量)的长度(等于ω)小于波数矢量某个分量K的长度。
这怎么可能?难道整体比部分还小吗?是的,因为我们还有虚数,只要其他动量分量为虚数,被考察的动量分量幅度,就可以比整个动量矢量的幅度还大。
正因为其他动量分量从实数变为虚数,原来的波动因子变为衰减因子,使得倏逝波随距离成指数衰减。
超透镜的分类和工作原理
超级透镜的特点在于能够让倏逝波到达成像面参与成像,在这一过程中,由贵重金属(如Au,Ag 等)制成的超透镜的表面等离子体极化起到了关键作用。
围
绕着倏逝波的放大或恢复问题,人们发展了几种不同的超级透镜。
近场超透镜:
图1
Pendry的完美透镜:这种近场透镜的特点是可以让行波正常通过,而让倏逝波在超透镜中传播时得到增强,但出透镜之后又和原来一样衰减,因此只能在近场成像。
图2
人们研究发现,倏逝波在通过银平板后,在一定厚度范围内振幅以指数增强。
2005年,加州大学伯克利分校的科学家用“PMMA-Ag-光刻胶”的混合集成进行了超透镜原理验证实验,银膜超透镜通过表面等离子体的激发显著的改善了近场成像的清晰度,实验结果证明其分辨率高达λ/6,可以使60nm的细节清晰成像。
SiC近场超分辨透镜,实现λ/20的分辨率。
近场超透镜只能实现近场成像,从图1中可以看出,倏逝波通过超透镜得到增强,但是它一旦传播出透镜又会很快衰减。
近场成像只能用近场扫描光学显微镜观察,因此这种超透镜在很多应用中将受限。
远场超透镜
1、远场无放大效果
(1)远场成像无法用普通显微镜看的
美国东北大学的远场超分辨透镜,λ/6的分辨率,采用的近场扫描光学显微镜观察。
(2)可以用传统显微镜观察
远场超透镜的出光口处加入了一些亚波长尺寸的波纹状微结构(比如亚波长光栅)。
微结构的作用是将出透镜之后的光波由倏逝波转化为行波。
因为物体发射的光经过光栅后会形成不同的衍射级次,经过特殊设计的微结构起到了选择的作用,只有行波的0级和倏逝波的-1级可以在通过透镜以后传输到远场,因此在超透镜效应下被增强的倏逝波在出射透镜以后能够被转化为行波。
光栅衍射时满足k out=k in+m*k d,其中k d= 2π/d,k out、k in分别表示出射和入射波矢,d是光栅周期,m是衍射极次。
通过选择适当的参数,就能将高频的倏逝波衍射成波矢相对较小可以传播到远场的传播波,这样在远场再通过适当的装置将转化后的传播波还原成原来的倏逝波,从而在远场得到了完整的信息,实现了远场成像。
2、双曲透镜(远场放大)
双曲透镜,其称呼来自柱面坐标系的两个波矢分量满足双曲线变化关系。
其原理如下图所示,由于双曲透镜的特殊半圆柱腔结构,各向异性的介质材料具有双曲线结构的色散曲线,倏逝波一旦进入双曲透镜便被转化为行波,出射透镜后横波成分被压缩到无限小,即在出射以后仍为行波,并且在远场成放大的清晰像。
2007年加州大学伯克利分校的Liu Z.等人利用在石英衬底上Ag和Al
2O
3
交替
构造半圆柱膜层,实现了50nm线条图形的放大传递。
曼彻斯特大学、新加坡国立大学提出的用SiO2微球实现超分辨成像。
工作波段可见光,分辨率50nm,放大倍率8-14倍。
存在的问题:
1、超透镜必须距离样品非常近,以保证倏逝波能进入透镜。
2、超透镜本身的材料损耗很大,限定了透镜的分辨率。
3、超透镜本身很小,使得其的视场非常小,且成像存在畸变失真。
4、无法观察活的细胞等。
5、。