自组织特征映射网的应用
- 格式:docx
- 大小:60.88 KB
- 文档页数:4


人工神经网络历史发展及应用综述1、引言人类为了生存在改造探索自然的过程中,学会利用机械拓展自身的体力,随着对自然认识的不断深入,创造语言,符号,算盘、计算工具等来强化自身脑力。
复杂的数字计算原本是靠人脑来完成的,为了摆脱这种脑力束缚发明了计算机。
其数字计算能力比人脑更强,更快、更准。
计算机的出现,人类开始真正有了一个可以模拟人类思维的工具,期盼可以实现人工智能,构造人脑替代人类完成相应工作。
要模拟人脑的活动,就要研究人脑是如何工作的,要怎样模拟人脑的神经元。
人脑的信息处理具有大规模并行处理、强容错性和自适应能力、善于联想、概括、类比和推广的特点,多少年以来,人们从生物学、医学、生理学、哲学、信息学、计算机科学、认知学、组织协同学等各个角度企图获悉人脑的工作奥秘,寻求神经元的模拟方法。
在寻找上述问题答案的研究过程中,从20世纪40年代开始逐渐形成了一个新兴的边缘性交叉学科,称之为“神经网络”,是人工智能、认知科学、神经生理学、非线性动力学、信息科学、和数理科学的“热点”。
关于神经网络的研究包含众多学科领域,涉及数学、计算机、人工智能、微电子学、自动化、生物学、生理学、解剖学、认知科学等学科,这些领域彼此结合、渗透,相互推动神经网络研究和应用的发展。
2、定义思维学普遍认为,人类大脑的思维有三种基本方式,分为抽象(逻辑)思维、形象(直观)思维和灵感(顿悟)思维。
逻辑性的思维是根据逻辑规则进行推理的过程,这一过程可以写成指令,让计算机执行,获得结果。
而直观性(形象)的思维是将分布式存储的信息综合起来,结果是忽然间产生想法或解决问题的办法。
这种思维方式的有以下两个特点:一是信息通过神经元上的兴奋模式分布储在网络上;二是信息处理通过神经元之间同时相互作用的动态过程来完成的。
人工神经网络就是模拟第二种人类思维方式。
人工神经网络是由大量具备简单功能的人工神经元相互联接而成的自适应非线性动态系统。
虽然单个神经元的结构和功能比较简单,但大量神经元连接构成的网络系统行为却异常复杂。

SOFM⽹络SOFM⽹络及其在MATLAB中的实现朱福珍吴斌(西南科技⼤学信息⼯程学院,四川绵阳 621002 )摘要本⽂详细叙述了⾃组织映射⽹络的原理、算法及其在Matlab中实现的⼯具箱,并结合实例给出了SOFM在Matlab上的实现⽅法,对于SOFM的现存问题和未来研究趋势作了分析和展望。
关键词⾃组织;⾃组织特征映射(SOFM); 拓扑结构中⽂分类号:TP183 ⽂献标识码:A ⽂章编号: SOFM Network and the Realization of SOFM in MatlabZhu Fu-Zhen Wu Bin(College of Information and Engineering, SWUST,Mianyang,Sichuan,621002,China) Abstract: This paper described the principle, the algorithm and the toolbox in Matlab of Self-organizing Feature Map Neural Network detailedly, including a paradigm of SOFM implemented in Matlab, analyzed the problem of SOFM at present and prospected its researching trend in the future.Key Words: Self-organization; Self-organizing Feature Map; Topology Structure引⾔⼈⼯神经⽹络(Artificial Neural Network,简称ANN)是近年来发展起来的模拟⼈脑⽣物过程的⼈⼯智能技术。
它由⼤量简单的神经元⼴泛互连形成复杂的⾮线性系统[1],不需要任何先验公式,就能从已有数据中⾃动地归纳规则,获得这些数据的内在规律,具有很强的⾃学习、⾃组织、⾃适应和⾮线性映射能⼒,特别适合于因果关系复杂的⾮线性推理、判断、识别和分类等问题。



自组织特征映射神经网络研究与应用自组织特征映射神经网络,又称Kohonen网络,在机器学习领域中具有广泛的研究和应用价值。
它是由芬兰科学家Teuvo Kohonen于1982年提出的,用来解决模式分类和聚类问题。
本文将分别从网络结构、学习规则、应用场景等多个角度来介绍自组织特征映射神经网络的研究与应用。
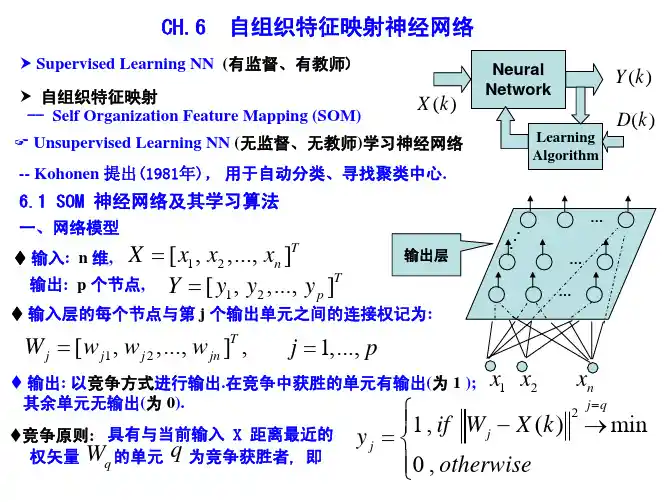
一、网络结构自组织特征映射神经网络是一种有两层或多层的神经元组成的全连接网络,其特点是每个神经元与输入节点全连接,但只有部分神经元与输出节点连接,这些与输出节点相连接的神经元被称作胜者神经元。
胜者神经元的选择根据输入数据与神经元之间的权值距离进行,即越接近输入数据的神经元越容易胜出。
自组织特征映射神经网络的网络结构简单,但它可以通过适当调整参数,从而实现多种复杂的函数映射。
在具体应用中,还可以采用层级结构的自组织特征映射神经网络,对于复杂的数据集,可以通过层层处理,逐步提取其更高层次的特征。
二、学习规则自组织特征映射神经网络的学习规则是基于竞争性学习的,其原理是将输入数据投影到高维空间中的低维网格上,使其可以进行分类和聚类。
其学习过程中所用的算法有两种:批处理算法和在线算法。
批处理算法在每个Epoth后,在一个批次中对全部样本进行训练,并更新权值,从而可以获得更稳定的结果,但训练时间较长。
而在线算法则是对每个样本逐个进行学习,因此训练速度较快,但结果相对不稳定。
在学习过程中,自组织特征映射神经网络会通过不断调整权值,形成特征抽取与分类能力强的模型。
其学习的结果可以通过可视化方式,将数据点在网格上的分布呈现出来,形成热图的形式,便于分析与理解。
三、应用场景自组织特征映射神经网络在数据挖掘、图像处理、生物信息学等领域都有着广泛的应用。
在图像处理领域中,可以通过自组织特征映射神经网络对图像进行压缩和分类。
在数据挖掘方面,自组织特征映射神经网络可用于数据聚类和数据可视化。
通过自组织特征映射神经网络,大量数据可以被投射到低维空间,并形成可视化热图,从而能够更好地理解数据的分布规律。


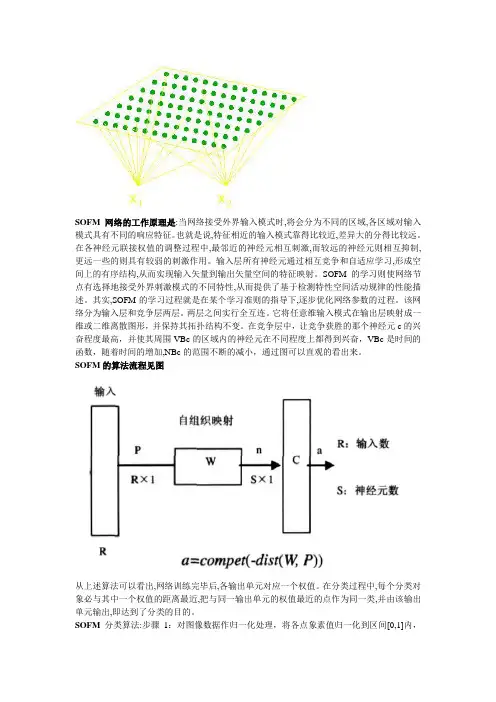
SOFM网络的工作原理是:当网络接受外界输入模式时,将会分为不同的区域,各区域对输入模式具有不同的响应特征。
也就是说,特征相近的输入模式靠得比较近,差异大的分得比较远。
在各神经元联接权值的调整过程中,最邻近的神经元相互刺激,而较远的神经元则相互抑制,更远一些的则具有较弱的刺激作用。
输入层所有神经元通过相互竞争和自适应学习,形成空间上的有序结构,从而实现输入矢量到输出矢量空间的特征映射。
SOFM的学习则使网络节点有选择地接受外界刺激模式的不同特性,从而提供了基于检测特性空间活动规律的性能描述。
其实,SOFM的学习过程就是在某个学习准则的指导下,逐步优化网络参数的过程。
该网络分为输入层和竞争层两层。
两层之间实行全互连。
它将任意维输入模式在输出层映射成一维或二维离散图形,并保持其拓扑结构不变。
在竞争层中,让竞争获胜的那个神经元c的兴奋程度最高,并使其周围VBc的区域内的神经元在不同程度上都得到兴奋,VBc是时间的函数,随着时间的增加,NBc的范围不断的减小,通过图可以直观的看出来。
SOFM的算法流程见图从上述算法可以看出,网络训练完毕后,各输出单元对应一个权值。
在分类过程中,每个分类对象必与其中一个权值的距离最近,把与同一输出单元的权值最近的点作为同一类,并由该输出单元输出,即达到了分类的目的。
SOFM分类算法:步骤1:对图像数据作归一化处理,将各点象素值归一化到区间[0,1]内,由此得到图像X=(x 1,x 2,…x n ),其中x i 为图像一点的归一化后的模式.步骤2:初始化网络连接权值W j ,其中1<=j<=M ,M 对应竞争层神经元向量元素的个数。
步骤3:选择获胜单元c,d c =j min ||x i -w j ||.步骤4:进行连接权调整邻域函数一般选用Gaussian 函数:NB(t)=exp{-d j,i (x)2)/2σ2}其中d j,i (x)表示邻域中神经元与获胜神经元间的距离,采用Euclid 距离计算;σ为邻域的有效半径,随离散时间指数衰减σ(t)=σ(0).exp(-t/τ1),t=0,1,2,∀,j=1,2,…m 的初始值,τ1为时间常数,σ(0)是σ(t)的初始值. 步骤5:按照以上步骤,反复训练每一个输入的模式值x i ,直至完成规定的训练次数.经过学习后,再次将x i 输入网络,其输出结果即为分类结果。

第6章自组织特征映射本章介绍Kohonen的自组织特征映射(Self-Organizing Feature Mapping,简称SOFM)[Koho1984]。
自组织特征映射是一种竞争学习网络,可以通过神经元之间的竞争实现大脑神经系统中的“近兴奋远抑制”功能,并具有把高维输入映射到低维的能力(拓扑保形特性)。
我们先介绍生物系统中的竞争现象,然后介绍SOFM的网络结构和学习算法,最后通过仿真例子演示SOFM的拓扑保形特性。
6.1 生物系统中的竞争在第4章介绍RBF网的生理学基础时,我们曾提到,某些视觉神经细胞在视网膜上有特定的感受野,并具有近兴奋远抑制(on-center off-surround)功能,因此我们用径向基函数建模这样的近兴奋远抑制神经元。
在本章,我们从神经元之间互相竞争的角度再来看这一现象。
生物神经网络的研究发现,大脑皮层中,神经元是呈2维空间排列的,而且邻近神经元之间通过侧反馈的方式紧密互联。
因此每个神经元既有外部区域的输入信号,也有来自同一区域其它神经元的反馈输入信号。
而邻近神经元之间侧反馈信号的强度体现为这些神经元之间的连接强度,因此而这些连接权值的分布也体现出明显的“近兴奋远抑制”现象。
更具体的说,以某个激活的神经元为圆心,邻近其它神经元根据与该神经元的距离,与之的连接权值呈三个区域的分布:对较邻近的神经元呈强的兴奋性侧反馈;对远邻的神经元呈抑制性侧反馈;对更远的神经元又呈弱的兴奋性侧反馈。
通常情况下,可以不考虑第三区的弱侧反馈。
这里所说的邻近神经元,在大脑皮层中是指以某兴奋神经元为圆心.半径约为50-500µm左右的其它神经元,而远邻神经元是指半径为200µm-2mm左右的神经元。
(a)(b)图6.1 生物神经元中的“近兴奋远抑制”另外,神经元之间连接强度从增强到抑制的过渡是平滑的,因此相邻神经元连接强1度的分布呈“墨西哥帽”式分布,如图6.1(a)所示。
基于自组织特征映射网的灰度图像二值化方法
摘要:
基于自组织特征映射网的灰度图二值化方法,所采用的自组织特征映射网络输入层只含有一个节点,其输入z为图像像素灰度值。
输出层是两个节点组成的一维阵列,输出Y=[y1,y2]=[0,255],由于输出层只有两个节点,所以网络的训练算法中不需考虑侧反馈。
关键词:SOFM,自组织特征映射网,灰度图像,二值化
一、SOFM 网络结构和原理
SOFM网络结构
自组织特征映射(SOFM)神经网络是芬兰神经网络专家Kohonen于1981年提出的,该网络的出发点是模拟大脑皮层中具有自组织特征的神经信号传送过程,属于无导师学习的竞争型神经网络。
其网络结构如图1所示,由输入层和竞争层组成,输入层由N个神经元组成,竞争层由M个输出神经元组成,且形成一个二维阵列。
输入层与竞争层各神经元之间实现全互连接,竞争层之间实行侧向连接。
网络根据其学习规则,对输入模式进行自动分类,即在无导师情况下,通过对输入模式的自组织。
学习,抽取各个输入模式的特征,在竞争层将分类结果表示出来。
图1
SOFM 的基本原理
SOFM 的基本原理是:当某类模式输入时,输出层某节点得到最大刺激而获胜,获胜节点周围的节点因侧向作用也受到刺激。
这时网络进行一次学习操作,获胜节点及周围节点的连接权值向量朝输入模式的方向作相应的修正。
当输入模式类别发生变化时,二维平面上的获胜节点也从原来节点转移到其它节点。
这样,网络通过自组织方式用大量样本数据来调整其连接权值,最后使得网络输出层特征图能够反映样本数据的分布情况。
SOFM网络的主要特性为:1)自组织排序性质,即拓扑保持能力;2)自组织
概率分布性质;3)以若干神经元同时反映分类结果,具有容错性;4)具有自联想功能。
SOFM网络的主要功能是实现数据压缩、编码和聚类,实际应用包括:模式识别、过程和系统分析、机器人、通信、数据挖掘以及知识发现等。
二、基于SOFM的图像二值化方法
基于自组织特征映射网的灰度图二值化方法,所采用的自组织特征映射网络输入层只含有一个节点,其输入z为图像像素灰度值。
输出层是两个节点组成的一维阵列,输出Y=[y1,y2]=[0,255],由于输出层只有两个节点,所以网络的训练算法中不需考虑侧反馈。
二值化算法分为两步:①对网络的两个权值w1和w2初始化。
然后,把一幅待处理的灰度图的像素作为样本,灰度值为样本特征,将所有像索灰度值依次输入SOFM网,经过一定次数的训练,网络的权值w1和w2分别逼近图像的背景类中心的灰度和目标类中心的灰度。
②以训练后的w1和w2作为网络的权值,重新将所有像素灰度值输入网络按欧
氏距离进行竞争判断,若某一像素靠近背景类中心w1,则输出节点y1获胜,该像素被二值化为“0”(黑色);若某一像素靠近目标类中心w2,则输出节点y2获胜,该像素被二值化为“255”(白色)。
当所有像素参于竞争判断后,即完成了灰度图的二值化。
三、二值化过程中几个问题的讨论
在网络开始训练时,由于权值的初始值可随机选择,W-和w。
的大小次序不定,所代表的类中随其大小次序不同而变化。
这样,对于网络输出层的两个节点,就难以判断到底哪一个节点代表目中心或背景类中心,使得经过二值化的图像,目标和背景的黑自颜色随机变化。
由于灰度值的大小度图中区分目标和背景的一种特征,SOFM网的自组织学习能力使得小的权值吸引灰度值较小的,大的权值吸引灰度值较大的像素。
因此解决方法是,在对权值w1和w2初始化后,通过大小比较,把小的权值放在w1,把大的权值放在w2,使之有序化,这样可保证二值化后背景灰度值恒为0,目标灰度值恒为255。
虽然网络权值的初始化一般可选择很小的随机数,但由于初始权值离目
标和背景类中心较远,训练次数和花费的时间多。
因此,应尽可能将初始权值选在目标和背景类中心附近。
为了做到这一点,可以先用整个图像的灰度平均值将像素分成两组,再求出两组像素各自的灰度平均值,作为初始权值,可大大减少训练次数。
该算法虽然不直接求灰度阈值,但通过聚类找到的目标和背景两个
灰度中心反映了整体阈值的存在,本质上仍属于整体阈值法。
经过实例观察发现,目标和背景两个灰度中心的平均值即为整像的灰度阈值。
因此,对于某些受噪声干扰严重的图像(其灰度直方图中的目标灰度分布区域与背度分布区域相互交错),该算法处理效果不如局部阔值二值化方法。
解决这个问题,可以考虑把的局部灰度特性与整体灰度分布特性相结合作为二值化的依据。
四、总结
该算法来源于合肥工业大学的学报上发表的一篇论文,是自组织特征映射网一个具体应用例子。
该算法主要叙述了一种基于SOFM的灰度图像二值化方法,利用SOFM网络良好的聚类特性,对256色灰度图的像素按灰度值聚类,从而找到目标与背景两个类中心,通过所有像素与目标和背景类中心的灰度距离竞争达到二值化。
五、参考文献
[1] 刘峡壁.人工智能导论-方法与系统.北京:国防工业出版社,2008
[2] 方敏.基于自组织特征映射网的灰度图像二值化方法[J].合肥工业
大学学报(自然科学版),2001,24(6)。