运动学作业解答 学
- 格式:ppt
- 大小:357.00 KB
- 文档页数:10
高中物理运动学习题及答案(三)41. 一石头以速度20米/秒在悬崖上竖直向上抛出。
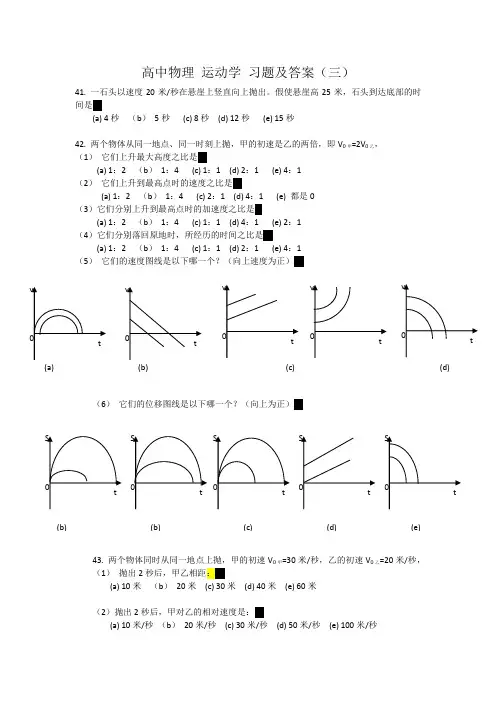
假使悬崖高25米,石头到达底部的时间是(b)(a) 4秒(b)5秒(c) 8秒(d) 12秒(e) 15秒42. 两个物体从同一地点、同一时刻上抛,甲的初速是乙的两倍,即V0甲=2V0乙,(1)它们上升最大高度之比是(e)(a) 1:2 (b)1:4 (c) 1:1 (d) 2:1 (e) 4:1(2)它们上升到最高点时的速度之比是(e)(a) 1:2 (b)1:4 (c) 2:1 (d) 4:1 (e) 都是0(3)它们分别上升到最高点时的加速度之比是©(a) 1:2 (b)1:4 (c) 1:1 (d) 4:1 (e) 2:1(4)它们分别落回原地时,所经历的时间之比是(d)(a) 1:2 (b)1:4 (c) 1:1 (d) 2:1 (e) 4:1(5)它们的速度图线是以下哪一个?(向上速度为正)(b)(6)它们的位移图线是以下哪一个?(向上为正)(a)43. 两个物体同时从同一地点上抛,甲的初速V0甲=30米/秒,乙的初速V0乙=20米/秒,(1)抛出2秒后,甲乙相距:(b)(a) 10米(b)20米(c) 30米(d) 40米(e) 60米(2)抛出2秒后,甲对乙的相对速度是:(a)(a) 10米/秒(b)20米/秒(c) 30米/秒(d) 50米/秒(e) 100米/秒44. 两个物体在同一地点在珠初速V 0米/秒先后下抛,甲先乙3秒,乙抛出后:(1) 甲相对乙的相对速度是:(以米/秒为单位)(d)(a) V 0 (b ) 2V 0 (c) 3 V 0 (d) 3g (e) V 0+3g(2) 它的速度图线是以下哪一个?(e)45. 一辆汽车以加速度a 起动时,有一辆自行车以速度V 0从旁驶过。
(i) 下面关于两者运动情况的描述哪几句正确?©(1) 汽车追不上自行车,因为汽车起动时速度小(2) 汽车追得上自行车,因为汽车速度越来越大,后来大于自行车的速度(3) 汽车与自行车的距离不断减小,最后追上(4)汽车与自行车的距离开始不断增加,直到两者速度相等时,然后开始逐渐减小,直到相遇(ii ) 对不同参照物运动的描述,下面哪几句正确?(a)(1) 以自行车为参照物,汽车是开始速度方向向后的匀减速运动,类似上抛运动(2) 以汽车为参照物,自行车是开始速度方向向前的匀减速运动(3) 以地面为参照物,汽车是初速为零的匀加速运动,自行车作匀速运动(4) 以汽车为参照物,汽车作初速为零的匀加速运动(iii) 骑自行车的人,看到汽车运动的位移变化图线是以下哪个所示、(设与V 0相反的方向为正向)(b)(iv) 汽车追上自行车的时间是(b)(a)V0a (b) 2V0a(c)√Voa(d)V0a (e)(b)(c) (e)46.从加速上升的汽球上释放一物。

一.选择题(共28小题)1.(2014•陆丰市校级学业考试)某一做匀加速直线运动的物体,加速度是2m/s2,下列关于该物体加速度的理解正确的是()A.每经过1秒,物体的速度增加1倍B.每经过1秒,物体的速度增加2m/sC.物体运动的最小速度是2m/sD.物体运动的最大速度是2m/s2.(2014•廉江市校级学业考试)下列描述的运动,能找到实例的是()A.物体运动的加速度不断变化,而物体的动能却保持不变B.物体运动的加速度等于零,而速度却不等于零C.物体运动的加速度不等于零,而速度保持不变D.物体作曲线运动,但具有恒定的加速度3.(2014•越秀区校级三模)关于物体运动状态的改变,下列说法中正确的是()A.运动物体的加速度不变,则其运动状态一定不变B.物体的位置在不断变化,则其运动状态一定在不断变化C.做直线运动的物体,其运动状态可能不变D.做曲线运动的物体,其运动状态也可能不变4.(2013秋•江西期末)下列关于速度和加速度的说法中,正确的是()A.加速度表示速度变化的大小B.物体的速度为零,加速度也一定为零C.运动物体的加速度越来越小,表示速度变化越来越慢D.运动物体的加速度越来越小,表示物体运动的速度也越来越小5.(2013秋•龙华区校级期末)足球以8m/s的速度飞来,运动员把足球以12m/s的速度反向踢出,踢球时间为0.2s,设足球飞来的方向为正方向,则这段时间内足球的加速度是()A.﹣200m/s2B.200m/s2C.﹣100m/s2D.100m/s26.(2013秋•天山区校级期末)关于速度和加速度,以下说法中正确的是()A.速度表示物体位置变化的大小和方向B.物体的加速度增大,物体的速度可能减小C.物体的速度改变量△v越大,加速度一定越大D.加速度表示物体速度变化的大小和方向7.(2013秋•武陵区校级期末)已知一运动物体的初速度v0=5m/s,加速度a=﹣3m/s2,它表示()A.物体的加速度方向与速度方向相反,且物体的速度在增加B.物体的加速度方向与速度方向相同,且物体的速度在增加C.物体的加速度方向与速度方向相反,且物体的速度在减小D.物体的加速度方向与速度方向相同,且物体的速度在减小8.(2011秋•瑶海区校级期中)物体从静止开始做匀加速直线运动,已知第2s内位移为x,则物体运动的加速度大小为()A.B.C.D.9.(2015•沈阳校级模拟)一物体从H高处自由下落,经时间t落地,则当它下落时,离地的高度为()A.B.C.D.10.(2015•嘉定区一模)用如图的方法可以测出一个人的反应时间,设直尺从静止开始自由下落,到直尺被受测者抓住,直尺下落的距离h,受测者的反应时间为t,则下列结论正确的是()A.t∝h B.C.t∝D.t∝h2t∝11.(2014•吉林一模)科技馆中的一个展品如图所示,在较暗处有一个不断均匀滴水的水龙头,在一种特殊的灯光照射下,可观察到一个下落的水滴,缓缓调节水滴下落的时间间隔到适当情况,可以看到一种奇特的现象,水滴似乎不再下落,而是像固定在图中的A、B、C、D四个位置不动,一般要出现这种现象,照明光源应该满足(g=10m/s2)()A.普通光源即可B.间歇发光,间隔时间0.4sC.间歇发光,间隔时间0.14s D.间歇发光,间隔时间0.2s12.(2014秋•宝安区校级期中)为了求高层建筑的高度,从楼顶上自由下落一光滑小石子,除了知道当地的重力加速度以外,还需要知道下述哪个量()A.第一秒末的速度B.第一秒内的位移C.最后一秒的位移D.最后一秒的初速度13.(2014秋•雨城区校级期末)甲、乙两物体所受的重力之比为1:2,甲,乙两物体所在的位置高度之比为2:1,它们各自做自由落体运动,则()A.落地时的速度之比是:1B.落地时的速度之比是1:1C.下落过程中的加速度之比是1:2D.下落过程中加速度之比是2:114.(2014春•正定县校级期末)从地面竖直上抛一物体A,同时在离地面某一高度处有另一物体B自由落下,两物体在空中同时到达同一高度时速率都为υ,则下列说法中正确的是()A.物体A上抛的初速度和物体B落地时速度的大小相等,都是2υB.物体A、B在空中运动的时间相等C.物体A能上升的最大高度和B开始下落的高度相同D.两物体在空中同时达到同一高度处一定是B物体开始下落时高度的中点15.(2013秋•忻府区校级期末)一观察者发现,每隔一定时间有一滴水自8m高的屋檐落下,而且看到第五滴水刚要离开屋檐时,第一滴水正好落到地面,那么,这里第二滴离地面的高度是()A.2m B.2.5m C.2.9m D.3.5m16.(2014秋•淮南期末)自由下落的质点落地之前,第n秒内的位移与前(n﹣1)秒内的位移之比为()A.B.C.D.17.(2014秋•成都期末)如图所示,将一小球从竖直砖墙的某位置由静止释放.用频闪照相机在同一底片上多次曝光,得到了图中1、2、3…所示的小球运动过程中每次曝光的位置.已知连续两次曝光的时间间隔均为T,每块砖的厚度均为d.根据图中的信息,下列判断正确的是()A.位置1是小球释放的初始位置B.小球下落的加速度为C.小球在位置3的速度为D.能判定小球的下落运动是否匀变速18.(2014秋•北林区校级期末)做自由落体运动的物体,下落到全程一半时经历的时间是t,全程的下落时间为T,则t:T为()A.1:2 B.2:3 C.:2 D.:19.(2014秋•滕州市校级期中)在塔顶上将一物体以20m/s初速度竖直向上抛出,抛出点为A,不计空气阻力,设塔足够高,则物体位移大小为10m时,物体通过的路程可能为(g取10m/s2)()A.10 m B.20 m C.30 m D.50 m20.(2014•上海)在离地高h处,沿竖直方向向上和向下抛出两个小球,他们的初速度大小均为v,不计空气阻力,两球落地的时间差为()A.B.C.D.21.(2014•甘肃模拟)近年来有一种测g值的方法叫“对称自由下落法”:将真空长直管沿竖直方向放置,自其中O点向上抛小球又落至原处的时间为T2在小球运动过程中经过比O点高H的P点,小球离开P点至又回到P点所用的时间为T1,测得T1、T2和H,可求得g等于()A.B.C.D.22.(2014•兰考县模拟)某物体以30m/s的初速度竖直上抛,不计空气阻力,g取10m/s2.5s内物体的()A.路程为25mB.位移大小为25m,方向向下C.速度改变量的大小为10m/sD.平均速度大小为5m/s,方向向上23.(2014春•金山区校级期末)一只气球以10m/s的速度匀速上升,某时刻在气球正下方距气球6m处有一小石子以20m/s的初速度竖直上抛,若g取10m/s2,不计空气阻力,则以下说法正确的是()A.石子一定能追上气球B.石子一定追不上气球C.若气球上升速度等于9m/s,其余条件不变,则石子在抛出后1s末追上气球D.若气球上升速度等于7m/s,其余条件不变,则石子在到达最高点时追上气球24.(2013秋•楚雄州期末)某物体以30m/s的初速度竖直上抛,不计空气阻力,g取10m/s2.5s内物体的()A.平均速率为13m/sB.位移大小为25m,方向竖直向下C.速度改变量的大小为50m/s,方向竖直向上D.平均速度大小为5m/s,方向竖直向上25.(2013秋•万州区校级期末)某物体以20m/s的初速度竖直上抛,不计空气阻力,g取10m/s2.下列对物体4s内的运动描述错误的是()A.上升最大高度20m B.位移大小为40mC.速度改变量的方向向下D.平均速率为10m/s26.(2013秋•秦州区校级期末)以初速v0竖直上抛的物体可达到的最大高度为H,为使它能达到的最大高度加倍,则初速度应增为()A.v0B.2v0C.v0D.4v027.(2013•洪泽县校级模拟)一个从地面竖直上抛的物体,它两次经过同一较低a点的时间间隔为T a,两次经过另一较高的b点的时间间隔为T b,则ab两点间的距离为()A.g(T a2﹣T b2)B.g(T a2﹣T b2)C.g(T a2﹣T b2)D.g(T a﹣T b)28.(2013秋•平江县校级月考)在以速度V上升的电梯内竖直向上抛出一球,电梯内观者看见小球经t秒后到达最高点,则有()A.地面上的人所见球抛出时的初速度为V0=gtB.升降机中的人看见球抛出的初速度为V0=gtC.地面上的人看见球上升的最大高度为h=gt2D.地面上的人看见球上升的时间也为t一.选择题(共28小题)1.B 2.ABD 3.C 4.C 5.C 6.B 7.C 8.D 9.C 10.C 11.C 12.CD 13.A 14.AC 15.D 16.D 17.BCD 18.C 19.ACD 20.A 21.A 22.D 23.BC 24.AD 25.B 26.A 27.A 28.B。


高中物理强基习题专题一:运动学一.选择题1.如图所示,湖中有一小船,有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动.设该人以匀速率v0 收绳,绳不伸长且湖水静止,小船的速率为v,则小船作( )(A) 匀加速运动,θcos 0v v = (B) 匀减速运动,θcos 0v v =(C) 变加速运动,θcos 0v v =( D) 变减速运动,θcos 0v v =(E) 匀速直线运动,0v v =答案:C2.如上题图1-5,此时小船加速度为( )A.0B.θθcos )tan (20l vC.lv 20)tan (θ D.θcos 0v 答案:B3.地面上垂直竖立一高20.0 m 的旗杆,已知正午时分太阳在旗杆的正上方,求在下午2∶00 时,杆顶在地面上的影子的速度的大小为( )A.s m /1094.13-⨯B.s m /1094.14-⨯C.0D.s m /100.35-⨯答案:A解析:设太阳光线对地转动的角速度为ω,从正午时分开始计时,则杆的影长为s =htg ωt,下午2∶00 时,杆顶在地面上影子的速度大小为132s m 1094.1cos d d --⋅⨯===tωωh t s v二.计算题4.质点沿直线运动,加速度a =4 -t2 ,式中a 的单位为m ·s-2 ,t 的单位为s.如果当t =3s时,x =9 m,v =2 m ·s-1 ,求质点的运动方程.解析: 由分析知,应有⎰⎰=t t a 0d d 0vv v 得 03314v v +-=t t (1)由 ⎰⎰=t xx t x 0d d 0v 得 00421212x t t t x ++-=v (2) 将t =3s时,x =9 m,v =2 m ·s-1代入(1) (2)得v0=-1 m ·s-1,x0=0.75 m .于是可得质点运动方程为75.0121242+-=t t x 5.一石子从空中由静止下落,由于空气阻力,石子并非作自由落体运动,现测得其加速度a =A -Bv,式中A 、B 为正恒量,求石子下落的速度和运动方程.解析:本题亦属于运动学第二类问题,与上题不同之处在于加速度是速度v 的函数,因此,需将式dv =a(v)dt 分离变量为t a d )(d =v v 后再两边积分. 解:选取石子下落方向为y 轴正向,下落起点为坐标原点.(1) 由题意知 v v B A ta -==d d (1) 用分离变量法把式(1)改写为 t B A d d =-vv (2) 将式(2)两边积分并考虑初始条件,有⎰⎰=-t t B A 0d d d 0v v v v v 得石子速度 )1(Bt e B A --=v 由此可知当,t →∞时,B A →v 为一常量,通常称为极限速度或收尾速度. (2) 再由)1(d d Bt e BA t y --==v 并考虑初始条件有 t eB A y tBt yd )1(d 00⎰⎰--= 得石子运动方程)1(2-+=-Bt e B A t B A y6.质点在Oxy 平面内运动,其运动方程为r =2.0ti +(19.0 -2.0t2 )j,式中r 的单位为m,t 的单位为s .求:(1)质点的轨迹方程;(2) 在t1=1.0s 到t2 =2.0s 时间内的平均速度;(3) t1 =1.0s时的速度及切向和法向加速度;(4) t =1.0s 时质点所在处轨道的曲率半径ρ.解析:根据运动方程可直接写出其分量式x =x(t)和y =y(t),从中消去参数t,即得质点的轨迹方程.平均速度是反映质点在一段时间内位置的变化率,即t ΔΔr =v ,它与时间间隔Δt 的大小有关,当Δt →0 时,平均速度的极限即瞬时速度td d r =v .切向和法向加速度是指在自然坐标下的分矢量a t 和an ,前者只反映质点在切线方向速度大小的变化率,即t t te a d d v =,后者只反映质点速度方向的变化,它可由总加速度a 和a t 得到.在求得t1 时刻质点的速度和法向加速度的大小后,可由公式ρa n 2v =求ρ. 解 (1) 由参数方程x =2.0t, y =19.0-2.0t2消去t 得质点的轨迹方程:y =19.0 -0.50x2(2) 在t1 =1.00s 到t2 =2.0s时间内的平均速度j i r r 0.60.2ΔΔ1212-=--==t t t r v (3) 质点在任意时刻的速度和加速度分别为j i j i j i t ty t x t y x 0.40.2d d d d )(-=+=+=v v v j j i a 222220.4d d d d )(-⋅-=+=s m ty t x t 则t1 =1.00s时的速度v(t)|t =1s=2.0i -4.0j切向和法向加速度分别为t t y x t t t tt e e e a 222s 1s m 58.3)(d d d d -=⋅=+==v v v n n t n a a e e a 222s m 79.1-⋅=-=(4) t =1.0s质点的速度大小为122s m 47.4-⋅=+=y x v v v 则m 17.112==na ρv 8.已知质点的运动方程为j i r )2(22t t -+=,式中r 的单位为m,t 的单位为s.求:(1) 质点的运动轨迹;(2) t =0 及t =2s时,质点的位矢;(3) 由t =0 到t =2s内质点的位移Δr 和径向增量Δr ;*(4) 2 s 内质点所走过的路程s .分析 质点的轨迹方程为y =f(x),可由运动方程的两个分量式x(t)和y(t)中消去t 即可得到.对于r 、Δr 、Δr 、Δs 来说,物理含义不同,可根据其定义计算.其中对s 的求解用到积分方法,先在轨迹上任取一段微元ds,则22)d ()d (d y x s +=,最后用⎰=s s d 积分求s.解 (1) 由x(t)和y(t)中消去t 后得质点轨迹方程为 2412x y -= 这是一个抛物线方程,轨迹如图(a)所示.(2) 将t =0s和t =2s分别代入运动方程,可得相应位矢分别为j r 20= , j i r 242-=图(a)中的P 、Q 两点,即为t =0s和t =2s时质点所在位置.(3) 由位移表达式,得j i j i r r r 24)()(Δ020212-=-+-=-=y y x x 其中位移大小m 66.5)(Δ)(ΔΔ22=+=y x r 而径向增量m 47.2ΔΔ2020222202=+-+=-==y x y x r r r r *(4) 如图(B)所示,所求Δs 即为图中PQ 段长度,先在其间任意处取AB 微元ds,则22)d ()d (d y x s +=,由轨道方程可得x x y d 21d -=,代入ds,则2s内路程为 m 91.5d 4d 402=+==⎰⎰x x s s QP9.一质点P 沿半径R =3.0 m 的圆周作匀速率运动,运动一周所需时间为20.0s,设t =0 时,质点位于O 点.按(a)图中所示Oxy 坐标系,求(1) 质点P 在任意时刻的位矢;(2)5s时的速度和加速度.分析 该题属于运动学的第一类问题,即已知运动方程r =r(t)求质点运动的一切信息(如位置矢量、位移、速度、加速度).在确定运动方程时,若取以点(0,3)为原点的O ′x ′y ′坐标系,并采用参数方程x ′=x ′(t)和y ′=y ′(t)来表示圆周运动是比较方便的.然后,运用坐标变换x =x0 +x ′和y =y0 +y ′,将所得参数方程转换至Oxy 坐标系中,即得Oxy 坐标系中质点P 在任意时刻的位矢.采用对运动方程求导的方法可得速度和加速度.解 (1) 如图(B)所示,在O ′x ′y ′坐标系中,因t Tθπ2 ,则质点P 的参数方程为t T R x π2sin =', t T R y π2cos -=' 坐标变换后,在Oxy 坐标系中有 t T R x x π2sin='=, R t T R y y y +-=+'=π2cos 0 则质点P 的位矢方程为j i r ⎪⎭⎫ ⎝⎛+-+=R t T R t T R π2cos π2sin j i )]π1.0(cos 1[3)π1.0(sin 3t t -+=(2) 5s时的速度和加速度分别为j j i r )s m π3.0(π2sin π2π2cos π2d d 1-⋅=+==t TT R t T T R t v i j i r a )s m π03.0(π2cos )π2(π2sin )π2(d d 222222-⋅-=+-==t TT R t T T R t10.如图所示,半径为R 的半圆凸轮以等速v0沿水平面 向右运动,带动从动杆AB 沿竖直方向上升,O 为凸轮圆心,P 为其顶点.求:当∠AOP=α时,AB 杆的速度和加速度.根据解析:速度的合成,运用平行四边形定则,得:v 杆=v0tan α。

运动学【1】物体沿直线向同一方向运动,通过两个连续相等的位移的平均速度分别为v 1=10m/s 和v 2=15m/s ,则物体在这整个运动过程中的平均速度是多少? 【分析与解答】设每段位移为s ,由平均速度的定义有v =212121212//22v v v v v s v s st t s +=+=+=12m/s [点评]一个过程的平均速度与它在这个过程中各阶段的平均速度没有直接的关系,因此要根据平均速度的定义计算,不能用公式v =(v 0+v t )/2,因它仅适用于匀变速直线运动。
【2】一质点沿直线ox 方向作加速运动,它离开o 点的距离x 随时间变化的关系为x=5+2t 3(m),它的速度随时间变化的关系为v=6t 2(m/s),求该质点在t=0到t=2s 间的平均速度大小和t=2s 到t=3s 间的平均速度的大小。
【分析与解答】当t=0时,对应x 0=5m ,当t=2s 时,对应x 2=21m ,当t=3s 时,对应x 3=59m ,则:t=0到t=2s 间的平均速度大小为2021x x v -==8m/st=2s 到t=3s 间的平均速度大小为1232x x v -==38m/s [点评]只有区分了求的是平均速度还是瞬时速度,才能正确地选择公式。
【3】一架飞机水平匀速地在某同学头顶飞过,当他听到飞机的发动机声音从头顶正上方传来时,发现飞机在他前上方与地面成600角的方向上,据此可估算出此飞机的速度约为声速的多少倍?【分析与解答】设飞机在头顶上方时距人h ,则人听到声音时飞机走的距离为:3h/3 对声音:h=v 声t 对飞机:3h/3=v 飞t 解得:v 飞=3v 声/3≈0.58v 声[点评]此类题和实际相联系,要画图才能清晰地展示物体的运动过程,挖掘出题中的隐含条件,如本题中声音从正上方传到人处的这段时间内飞机前进的距离,就能很容易地列出方程求解。
【4】如图所示,声源S 和观察者A 都沿x 轴正方向运动,相对于地面的速率分别为v S 和v A .空气中声音传播的速率为v p .设v S <v p ,v A <v p ,空气相对于地面没有流动.(1)若声源相继发出两个声信号,时间间隔为△t ,.请根据发出的这两个声信号从声源传播到观察者的过程,确定观察者接收到这两个声信号的时间间隔△t '.(2)请利用(1)的结果,推导此情形下观察者接收到的声波频率与声源发出的声波频率间的关系式.【分析与解答】: (1)如图所示,设为声源S 发出两个信号的时刻,为观察者接收到两个信号的时刻.则第一个信号经过时间被观察者A 接收到,第二个信号经过时间被观察者A 接收到.且设声源发出第一个信号时,S 、A 两点间的距离为L ,两个声信号从声源传播到观察者的过程中,它们运动的距离关系如图所示.可得由以上各式,得(2)设声源发出声波的振动周期为T ,这样,由以上结论,观察者接收到的声波振动 的周期T'为 。

第一章质点运动学一选择题1.以下说法中,正确的选项是:()A.一物体若拥有恒定的速率,则没有变化的速度;B.一物体拥有恒定的速度,但仍有变化的速率;C.一物体拥有恒定的加快度,则其速度不行能为零;D. 一物体拥有沿x 轴正方向的加快度而有沿x 轴负方向的速度。
解:答案是 D。
2.长度不变的杆 AB,其端点 A 以 v0匀速沿 y 轴向下滑动, B 点沿 x 轴挪动,则 B 点的速率为:()A . v0 sinB .v0 cos C.v0 tan D.v0 / cos解:答案是 C。
简要提示:设 B 点的坐标为 x, A 点的坐标为 y,杆的长度为l,则x2y2l 2对上式两边关于时间求导:dx dy0,因dxv,dyv0,所以2 x 2 ydtdt dt dt2xv2yv0 = 0即v=v0 y/x =v0tan所以答案是 C。
3.如图示,路灯距地面高为 H,行人身高为 h,若人以匀速 v 背向路灯行走,灯y人头A H vv0hθvx影sB选择题 3图选择题 2图则人头影子挪动的速度u 为()H h Hv h HA.vB.H H h H h 解:答案是 B 。
简要提示:设人头影子到灯杆的距离为 x ,则x s h , x Hs , x H H hdx H ds HvuH h dt Hdt h所以答案是 B 。
4. 某质点作直线运动的运动学方程为x = 3t-5t 3 + 6 (SI),则该质点作A. 匀加快直线运动,加快度沿 x 轴正方向.B. 匀加快直线运动,加快度沿 x 轴负方向.C. 变加快直线运动,加快度沿 x 轴正方向.D. 变加快直线运动,加快度沿x 轴负方向.()解: 答案是 D5. 一物体从某一确立高度以v 0 的初速度水平抛出,已知它落地时的速度为v t ,那么它的运动时间是: ()v t - v 0v t v 0v t2 22v v 0 v t A.B.C.gD.2 gg2 g解:答案是 C 。

运动学典型例题例1汽车从静止开始出发;在水平路上做匀加速直线运动;通过相距为38.4m 的甲乙两地需8s;经过乙地的速度是经过甲地时速度的2倍;求汽车的加速度和甲地离汽车出发点的距离..分析这是一道匀变规律的应用题..根据题给条件;可先从汽车在甲乙两地的速度关系;求出汽车从出发点到甲地的时间;再求加速度和甲地离汽车出发点的距离..解答设汽车的加速度为a;汽车从出发处到甲地所需时间为t;则汽车经过甲地时速度为v甲=at 1汽车经过乙地时速度为v乙=2v甲=at+8 2联立式12得t=8s由题意s乙=s甲+38.4 5用t=8s代上式得a=0.4m/s2说明应用匀变规律解题的步骤:1根据题意确定研究对象;2明确物体运动过程及其特点;3选择合适公式列方程;4求解;5考察结果的合理性..例2以v=36km/h的速度沿平直公路行驶的汽车;遇障碍物刹车后获得大小为4m/s2的加速度;求刹车后3s内汽车通过的路程..分析应先求汽车从刹车到停止运动所用的时间t0..解答v0=36km/h=10m/s v t=0因为t0<3s;故刹车后汽车通过的路程为说明象汽车这类运动;刹车后会停止运动;不会返回..例3客车以20m/s的速度行驶;突然发现同轨前方120m处有一列货车正以6m/s的速度同向匀速前进;于是客车紧急刹车;刹车引起的加速度大小为0.8m/s2;问两车是否相撞分析这是多个质点运动问题..两车不相撞的条件是:当客车减速到6m/s时;位移差△s=s货+s0-s客>0..解答设客车刹车后经时间t两车速度相同..即v2=6m/s此时两车相距为=-2.5m因为△s<0;故两车会相撞..说明该题中两车速度相等是一个临界状态;解答时应从这些特殊状态中寻找隐含条件;如本题中v2=6m/s这个条件..例4作匀加速直线运动的物体;在一段时间内通过一段位移;设这段时间中间时刻的速度用v1表示;这段位移中点的速度用v2表示;试比较v1与v2的大小..分析该题可应用中间时刻的速度公式和位移中点的速度公式求解..解答设这段时间内物体的初速度为v0;末速度为v t;则说明运用数学知识求解物理问题;这是高考对能力考查的内容之一;平时应予重视和培养..例5一个气球以4m/s的速度竖直上升;气球下系着一个重物;当气球上升到217m高度时;系重物的绳子断了;那么从这时起;重物要经过多长时间才落回地面g=10m/s2分析该题考察的重点是对运动过程和运动状态的分析..重物随气球上升;与气球具有相同的速度;分离时;重物则以4m/s的速度做竖直上抛运动..解答解法一分段分析法设重物分离后上升的最大高度为h;上升时间为t1;从最高点落回地面的时间为t1;整个时间为t..上升过程:重物做匀减速运动;则下落过程:重物做自由落体运动则重物从分离到落地经历的时间为:t=t1+t2=0.4+6.6=7s解法二整体分析法把重物从分离到落地的整个过程看作匀变速直线运动;落地点的位移为H=-217m;则则重物从分离到落地经历的时间为7s..说明1计算竖直上抛运动的有关问题;既可用分段法;也可用整体法;具体用哪种方法;视问题的性质和特点而定;解题时要注意各矢量的方向与正负取值..2本题属于“分离型”问题;要注意其特点;即分离时“母体”与“子体”具有相同的速度..例6升降机底板及顶板相距2.5m;现升降机从静止开始以加速度a=10m/s2竖直向上运动;某时顶板上一螺钉突然松脱;1求螺钉落到底板上需要多少时间2若螺钉在升降机运动1s后松脱;那么;在螺钉落向底板的时间内;螺钉对地位移是多少g=10m/s2分析1螺钉松脱后;相对升降机的加速度为a′=a+g;以升降机为参照物;匀变规律仍可适用;2螺钉松脱时与升降机同速;以后做竖直上抛运动..解答1螺钉相对升降机加速度为a′=a+g;初速度为v0=0;位移为h=2.5m;由匀变规律得:2螺钉松脱时速度为v0=at0=10×1=10m/s;螺钉松脱后作竖说明1求解该题第1问;选用升降机作参照物求解过程比较简单;但应注意加速度、速度、位移都必须是相对升降机这个参照物的值..2螺钉下落到底板上的时间是个定值;与下落时升降机的运动速度无关..3螺钉松脱后对地作坚直上抛运动;初速与松脱时刻有关..例7观察者站在列车第一节车厢的前端;列车从静止开始做匀加速运动..第一节车厢驶过他身边所用时间为t1;设每节车厢等长;求第n节车厢驶过他身边需要多少时间车厢之间的距离不计分析该题可利用公式和速度图像求解..解答解法一:设列车加速度为a;每节车厢长度为l;则又△t=t n-t n-1 4联立式1234解得:解法二:设第n节车厢通过观察者身边的初速度为v n-1;则解法三:作出列车的速度—时间图像;如图所示;根据图像的物理意义;图中两块阴影面积相等;即联立式1234解得:说明一道题从多个角度分析往往有多种解法;图像法解题可能是最简便的;平时应加强训练..通过“一题多解”能拓宽解题思路..不计每次碰撞时间;计算小球从开始下落到停止运动所经过的路程..分析小球每次反跳后均作竖直上抛运动;每次碰撞间经过的路程为反跳高度的2倍..小球第1、2、3……n次的反跳速度为小球从开始下落到第一次与地面相碰经过的路程为:l0=h0=5m说明本题求解的关键是找出速度、路程变化的规律;然后再应用数学知识解答..归纳推理法及数列求和公式在运动学问题的解答中经常用到..例8在2000m高空以v0=100m/s速度匀速水平飞行的飞机上每隔3s无初速相对飞机释放一包货物;问:1货物在空中排列成一个怎样的图形2空中有多少包货物3在空中相邻两包货物间的最大距离为多少4货物落在地面上的间距多少分析货物离开飞机后做平抛运动;在水平方向上;每包货物的运动状态相同;在竖直方向上按一定先后次序做自由落体运动..解答1由分析可知;货物在水平方向的运动状态完全相同;故货物在空中排在一条竖直线上;该竖直线以100m/s速度随飞机运动..2设货物落地时间为t;则∴在空中有7包货物..4△s=v0△t=100×3=300m说明求解本题的关健是要抓住货物脱离飞机后做平抛运动;再将其分解为水平方向和竖直方向两个分运动来分析;这样就容易找出其特点和规律..例9如图所示;A、B两小球之间用长6m的细线相连;将两球相隔0.8s先后从同一高度处以4.5m/s的初速度水平抛出;g取10m/s2;求:1A球抛出后经多长时间A、B两球连线可拉直2在这段时间内A球的位移多大分析当A、B拉直时;A、B间距离等于线长;求出A、B水平位移差△x和竖直位移差△y;由△x2+△y2=AB2即可求解..解答1A、B球的水平位移差为△x=v0△t=4.5×0.8=3.6mA、B球的竖直位移差为故t A=t B+△t=1s2s Ax=v0t A=4.5×1=4.5m小结求解相关运动问题要正确全面了解运动图景;从位移、时间方面寻找关系..。


一.选择题:[B]1、[基础训练2]一质点沿x轴作直线运动,其v-t曲线如图所示,如t=0时,质点位于坐标原点,则t=4.5 s时,质点在x轴上的位置为(A) 5m.(B) 2m.(C) 0.(D) -2 m.(E) -5 m.【答】4.5sx vdt=⎰,质点在x轴上的位置即为这段时间内v-t曲线下的面积的代数和:(1 2.5)22(21)122()x m=+⨯÷-+⨯÷=[A]2、[基础训练5] 一条河在某一段直线岸边同侧有A、B两个码头,相距1 km。
甲、乙两人需要从码头A到码头B,再立即由B返回。
甲划船前去,船相对河水的速度为4 km/h;而乙沿岸步行,步行速度也为4 km/h.如河水流速为2 km/h, 方向从A到B,则(A) 甲比乙晚10分钟回到A.(B) 甲和乙同时回到A.(C) 甲比乙早10分钟回到A.(D) 甲比乙早2分钟回到A.【答】甲:()()112()42423A B B At t t h→→=+=+=+-甲;乙:1122 ()42A B B A A Bt t t t h→→→=+==⨯=乙;∴1()10 (min)6t t t h∆=-==甲乙[C]3、[自测提高1]如图所示,湖中有一小船,有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动.设该人以匀速率v收绳,绳不伸长、湖水静止,则小船的运动是(A) 匀加速运动.(B) 匀减速运动.(C) 变加速运动.(D) 变减速运动.(E) 匀速直线运动.【答】如图建坐标系,设船离岸边x米,222l h x=+,22dl dxl xdt dt=,dx l dl dldt x dt x dt==,dlvdt=-,22dx h xv i v idt x+==--12223v hdv dv dxa idt dx dt x==⋅=-,可见,加速度与速度同向,且加速度随时间变化。
[B]4、(自测提高3)质点沿半径为R的圆周作匀速率运动,每T秒转一圈.在2T 时间间隔中,其平均速度大小与平均速率大小分别为(A) 2πR/T , 2πR/T.(B) 0 , 2πR/T(C) 0 , 0.(D) 2πR/T , 0.【答】平均速度大小:0rvt∆==∆平均速率:2s Rvt T∆==∆π[C]5、[自测提高6]某物体的运动规律为tkt2d/d vv-=,式中的k为大于零的常量.当0=t时,初速为v,则速度v与时间t的函数关系是(A)221vv+=kt, (B)221vv+-=kt,(C)2121vv+=kt, (D)2121vv+-=kt【答】tkt2d/d vv-=,分离变量并积分,2v tvdvktdtv=-⎰⎰,得2121vv+=kt.[B]6、[自测提高7]在相对地面静止的坐标系内,A、B二船都以2 m/s速率匀速行驶,A船沿x轴正向,B船沿y轴正向.今在A船上设置与静止坐标系方向相同的坐标系(x、y 方向单位矢用i、j表示),那么在A船上的坐标系中,B船的速度(以m/s为单位)为(A) 2i+2j.(B) -2i+2j.(C) -2i-2j.(D) 2i-2j.【答】B A对v=B对v地+A对v地=B对v地-A对v地=2222 (/)j i i j m s-=-+.二.填空题7、[基础训练10] 一物体作如图所示的斜抛运动,测得在轨道A点处速度v的大小为v,其方向与水平方向夹角成30°,则物体在A点的切向加速度a t = -0.5g ,轨道的曲率半径2vg.(重力加速度为g)【答】如图,将重力加速度分解为切向加速度分量和法向加速度分量,得2200sin300.5,cos30cos30t nv va g g a ggρρ=-=-==∴=8、[基础训练12] 一质点沿直线运动,其运动学方程为x = 6 t-t2(SI),则在t由0至4s的时间间隔内,质点的位移大小为 8 ()m,在t由0到4s的时间间隔内质点走过的路程为 10 ()m.【答】(1)x = 6 t-t2(SI),位移大小()24064408 ()r x x m∆=-=⨯--=;(2)62x dxv t dt==-,可见,t<3s 时,x v >0;t=3s 时,x v =0;而t>3s 时,x v <0;所以,路程=()()()3034()909810 ()x x x x m -+-=-+-=9、[基础训练13]在xy 平面内有一运动质点,其运动学方程为:jt i t r5sin 105cos 10+=(SI ),则t 时刻其速度=v(m/s) )5cos 5sin (50 j t i t+-;其切向加速度的大小a t = 0 ;该质点运动的轨迹是 圆 . 【答】(1)50(sin5cos5) (m/s)drv t i t j dt==-+; (2)速率50 /v m s =,切向加速度0t dva dt== (3)10cos5x t =,t y 5sin 10=,可见,22100x y +=,轨迹为一个圆。


刚体的基本运动8-2 搅拌机构如图所示,已知O 1A =O 2B =R ,O 1O 2=AB ,杆O 1A 以不变转速n rpm 转动。
试分析构件BAM 上M 点的轨迹及其速度和加速度。
解:搅拌机构BAM 作平动,故:22226030900M A B M A B nR Rn v v v R Rn a a a R ππωπω=========速度和加速度方向如图所示。
刚体的平面运动10-3 两齿条以速度v 1和v 2同向直线平动,两齿条间夹一半径为 r 的齿轮;求齿轮的角速度及其中心O 的速度。
解:(1) 齿轮作平面运动,取中心O 为基点,假设齿轮转动的角速度为ω;(2) 齿轮A 点和B 点的速度是12 o o v v r v v r ωω=+=-解方程得:1212 22o v v v vv rω+-== 10-4图示曲柄连杆机构中,曲柄OA = 40 cm ,连杆AB = 100 cm ,曲柄以转速n = 180 rpm绕O 轴匀速转动。
求当φ = 45o 时连杆AB 的角速度及其中点M 的速度。
解:(1) 连杆AB 作平面运动,选A 点为基点,B 点的速度为B A AB v v v =+已知2.4 /30sin sin 40sin sin sin 45=0.2828 16.43100A o nv OA OA m sOA OA AB ABπωπθϕθϕθ=⨯=⨯====⨯=应用正弦定理()()0000AB sin 45 2.4 5.56 /sin 45sin 90sin 9016.435.56 /AB A AB oABv v v m s v rad s ABπθω⨯===--==(2) M 点的速度M A AM v v v =+12.78 /2AM AB v v m s ==应用余弦定理v6.67 /M v m s ==注:本题也可以用速度瞬心法求连杆AB 的角速度和M 点的速度。
根据v A 和v B 得到AB 杆的速度瞬心C ;124.2 124.240135.6 120.0 OB cm AC OB OA cmMC cm===-=-===AB 杆的角速度:2.4 5.56 /1.356A AB v rad s ACπω=== M 点的速度:5.56 120.0667 /M AB v MC cm s ω=⨯=⨯=10-5图示四连杆机构中,OA = O 1B = 1/2AB ,曲柄以角速度ω=3 rad/s 绕O 轴转动;求在图示位置时杆AB 和杆O 1B 的角速度。
运动学练习1、已知图示平行四边形O1ABO2机构的O1A杆以匀角速度ω绕O1轴转动,试求D的速度和加速度。
2、一半径R= 0.2 m的圆轮绕定轴O沿逆时针方向转动,如图所示,轮的转动方程28t tϕ=−+(ϕ以rad计,t以s计)。
此轮边缘上绕一不可伸长的软绳,绳端挂一重物A。
试求当t = 2s时轮缘上任一点M和重物A的速度和加速度。
3、在图示系统中,滑块A以匀速度Av=1m/s向下运动,杆CD长1m,当α=45°、且杆CD水平时,试求AB杆和CD杆的角速度。
4、如图所示的机构中,已知O1O2=O1A=20cm, O1A杆以匀角速度13 rad/sω=绕O1转动。
试求图示位置套筒A相对于O2A杆的速度;O2A杆的角速度以及套筒A的科氏加速度(方向或转向均要在图中画出)5、 弯杆ABCD 以匀速度0ω绕轴A 转动,圆盘又以匀角速度ω绕轴D相对弯杆转动。
在图示瞬时,AD 连线为水平,圆盘边缘上的E 点与D 点的连线为铅直。
若已知L 、r ,并以E 点为动点,动系固结于弯杆上,试求E 点牵连速度和科氏加速度。
6、 杆CD 可沿水平槽移动,并推动杆AB 绕轴A 以匀角速度ω转动,L 为常数。
求图示位置θ=30°时CD 杆的绝对速度u 和绝对加速度a 。
7、 如图所示,直角曲杆OBC 绕O 轴转动,使套在其上的小环M 沿固定直杆OA 滑动,已知OB=0.1m ,OB 与BC 垂直,曲杆的角速度0.5rad/s ω=,角加速度为零,求当060ϕ=时小环M 的速度和加速度。
8、 凸轮在水平面上向右运动,凸轮半径为R ,在图示位置凸轮的速度为v ,加速度为a ,如图所示。
求图示瞬时AB 杆的速度、AB 杆的点A 相对于凸轮的速度以及AB 杆的加速度。
9、 半径为R 的半圆凸轮沿固定水平直线轨道以速度v 滑动,半径为R/2的滚轮沿凸轮轮廓滚动而不滑动。
在图示位置时30ϕ=,AC 水平。
试求该瞬时C 点的速度。
第1章质点运动学习题解答1-1如图所示,质点自A 点沿曲线运动到B 点A 点与B 点的矢径分别为°与g的头3s 内质点的位移、平均速度、平均加速度与所通过的路程 解:y 5 24t 2t 3,v 24 6t 2,a 12ty y(3) y(0) 18(m ) v - 6(m/s)3v(3) v(0)2、a18(m/ s )3t 2s 时,v 0,质点作反向运动s y(2)y(0) |y(3)y(2) | 46(m)1-3 一质点沿x 轴作直线运动,图示为其v t 曲 线图。
设t 0时,x 5m 。
试根据v t 图画出:(1) 质点的a t 曲线图;(2)质点的x t 曲线图。
试在图中标出位移 r 与路程s,同时对| r |与r 的意义及它们与矢径的关系进1-2 一质点沿y 轴作直线运动,其运动方程为y 5 24t 2t 3(SI)。
求在计时开始20 20t 解: 15 2.5t75 7.5t(0(2(6t 2)6)10)(1)20 20t 15 2.5t 75 7.5t(0(2(62)6)10)质点的a t曲线图如右图所示⑵v dxdt Xdxtvdt,可求得:t 2时,xdx 5 t0(20 20t)dt, 10t 2 20tt 6时,xdx 5 20(20 20t )dtt2(152.5t)dt ,5t215t 30410时,xdx20(20 20t)dt62(15 2.5t)dtt6(75 7.5t)dt , 75t 210210t 20t 5 (0 t 2)5t215t4%2 75t 4 门気105)30 (2 t 6)开口制上的覚皙變210 (6 t 10)质点的x t曲线图如右图所示。
1-4如图所示,路灯距地面的高度为H,在与路灯水平距离为s处,有一气球由离t 1 0 时,x(0) 0, y(0) 19,v x (0) 2—(0) 0地面h 处开始以匀速率v o 上升(h H )。
第一章 质点运动学1 -1 质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v ,t 至(t +Δt )时间内的位移为Δr , 路程为Δs , 位矢大小的变化量为Δr ( 或称Δ|r |),平均速度为v ,平均速率为v .(1) 根据上述情况,则必有( ) (A) |Δr |= Δs = Δr(B) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d s ≠ d r (C) |Δr |≠ Δr ≠ Δs ,当Δt →0 时有|d r |= d r ≠ d s (D) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d r = d s (2) 根据上述情况,则必有( )(A) |v |= v ,|v |= v (B) |v |≠v ,|v |≠ v (C) |v |= v ,|v |≠ v (D) |v |≠v ,|v |= v分析与解 (1) 质点在t 至(t +Δt )时间内沿曲线从P 点运动到P′点,各量关系如图所示, 其中路程Δs =PP′, 位移大小|Δr |=PP ′,而Δr =|r |-|r |表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注:在直线运动中有相等的可能).但当Δt →0 时,点P ′无限趋近P 点,则有|d r |=d s ,但却不等于d r .故选(B).(2) 由于|Δr |≠Δs ,故ts tΔΔΔΔ≠r ,即|v |≠v .但由于|d r |=d s ,故ts td d d d =r ,即|v |=v .由此可见,应选(C).1 -2 一运动质点在某瞬时位于位矢r (x,y )的端点处,对其速度的大小有四种意见,即(1)t rd d ; (2)t d d r; (3)t sd d ; (4)22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x . 下述判断正确的是( )(A) 只有(1)(2)正确 (B) 只有(2)正确(C) 只有(2)(3)正确 (D) 只有(3)(4)正确 分析与解tr d d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率.通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量;td d r 表示速度矢量;在自然坐标系中速度大小可用公式ts d d =v 计算,在直角坐标系中则可由公式22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=t y t x v 求解.故选(D).1 -3 质点作曲线运动,r 表示位置矢量, v 表示速度,a 表示加速度,s 表示路程, a t表示切向加速度.对下列表达式,即(1)d v /d t =a ;(2)d r /d t =v ;(3)d s /d t =v ;(4)d v /d t |=a t. 下述判断正确的是( )(A) 只有(1)、(4)是对的 (B) 只有(2)、(4)是对的 (C) 只有(2)是对的 (D) 只有(3)是对的 分析与解td d v 表示切向加速度a t,它表示速度大小随时间的变化率,是加速度矢量沿速度方向的一个分量,起改变速度大小的作用;tr d d 在极坐标系中表示径向速率v r (如题1 -2 所述);ts d d 在自然坐标系中表示质点的速率v ;而td d v 表示加速度的大小而不是切向加速度at.因此只有(3) 式表达是正确的.故选(D).1 -4 一个质点在做圆周运动时,则有( ) (A) 切向加速度一定改变,法向加速度也改变 (B) 切向加速度可能不变,法向加速度一定改变 (C) 切向加速度可能不变,法向加速度不变 (D) 切向加速度一定改变,法向加速度不变分析与解 加速度的切向分量a t起改变速度大小的作用,而法向分量a n 起改变速度方向的作用.质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的.至于a t是否改变,则要视质点的速率情况而定.质点作匀速率圆周运动时, a t恒为零;质点作匀变速率圆周运动时, a t为一不为零的恒量,当a t改变时,质点则作一般的变速率圆周运动.由此可见,应选(B).1 -5 已知质点沿x 轴作直线运动,其运动方程为32262t t x -+=,式中x 的单位为m,t 的单位为 s .求:(1) 质点在运动开始后4.0 s 内的位移的大小; (2) 质点在该时间内所通过的路程;(3) t =4 s 时质点的速度和加速度.分析 位移和路程是两个完全不同的概念.只有当质点作直线运动且运动方向不改变时,位移的大小才会与路程相等.质点在t 时间内的位移Δx 的大小可直接由运动方程得到:0Δx x x t -=,而在求路程时,就必须注意到质点在运动过程中可能改变运动方向,此时,位移的大小和路程就不同了.为此,需根据0d d =tx 来确定其运动方向改变的时刻t p ,求出0~t p 和t p ~t 内的位移大小Δx 1 、Δx 2 ,则t 时间内的路程21x x s ∆+∆=,如图所示,至于t =4.0 s 时质点速度和加速度可用tx d d 和22d d tx 两式计算.题 1-5 图解 (1) 质点在4.0 s 内位移的大小m 32Δ04-=-=x x x (2) 由 0d d =tx得知质点的换向时刻为s 2=p t (t =0不合题意)则m 0.8Δ021=-=x x xm 40Δ242-=-=x x x所以,质点在4.0 s 时间间隔内的路程为m 48ΔΔ21=+=x x s(3) t =4.0 s 时1s0.4sm 48d d -=⋅-==t tx v2s0.422m.s36d d -=-==t tx a1 -6 已知质点的运动方程为j i r )2(22t t -+=,式中r 的单位为m,t 的单位为s.求: (1) 质点的运动轨迹;(2) t =0 及t =2s时,质点的位矢;(3) 由t =0 到t =2s内质点的位移Δr 和径向增量Δr ;分析 质点的轨迹方程为y =f (x ),可由运动方程的两个分量式x (t )和y (t )中消去t 即可得到.对于r 、Δr 、Δr 、Δs 来说,物理含义不同,(详见题1-1分析).解 (1) 由x (t )和y (t )中消去t 后得质点轨迹方程为2412x y -=这是一个抛物线方程,轨迹如图(a)所示.(2) 将t =0s和t =2s分别代入运动方程,可得相应位矢分别为j r 20= , j i r 242-=图(a)中的P 、Q 两点,即为t =0s和t =2s时质点所在位置. (3) 由位移表达式,得j i j i r r r 24)()(Δ020212-=-+-=-=y y x x其中位移大小m 66.5)(Δ)(ΔΔ22=+=y x r而径向增量m 47.2ΔΔ2020222202=+-+=-==y x y x r r r r题 1-6 图1 -16 一质点沿半径为R 的圆周按规律2021bt t s -=v 运动,v 0 、b 都是常量.(1) 求t时刻质点的总加速度;(2) t 为何值时总加速度在数值上等于b ?(3) 当加速度达到b 时,质点已沿圆周运行了多少圈?分析 在自然坐标中,s 表示圆周上从某一点开始的曲线坐标.由给定的运动方程s =s (t ),对时间t 求一阶、二阶导数,即是沿曲线运动的速度v 和加速度的切向分量a t,而加速度的法向分量为a n =v 2 /R .这样,总加速度为a =a te t+a n e n .至于质点在t 时间内通过的路程,即为曲线坐标的改变量Δs =s t -s 0.因圆周长为2πR,质点所转过的圈数自然可求得.解 (1) 质点作圆周运动的速率为bt ts -==0d d v v其加速度的切向分量和法向分量分别为b ts a t -==22d d , Rbt Ra n 202)(-==v v故加速度的大小为R)(402222bt b a aa a t tn-+=+=v其方向与切线之间的夹角为⎥⎦⎤⎢⎣⎡--==Rb bt a a θt n20)(arctan arctan v(2) 要使|a |=b ,由b bt b R R=-+4022)(1v 可得 bt 0v =(3) 从t =0 开始到t =v 0 /b 时,质点经过的路程为bs s s t 220v =-=因此质点运行的圈数为bRRs n π4π22v ==1 -19 一无风的下雨天,一列火车以v 1=20.0 m·s-1 的速度匀速前进,在车内的旅客看见玻璃窗外的雨滴和垂线成75°角下降.求雨滴下落的速度v2 .(设下降的雨滴作匀速运动)题 1-19 图分析 这是一个相对运动的问题.设雨滴为研究对象,地面为静止参考系S,火车为动参考系S′.v 1 为S′相对S 的速度,v 2 为雨滴相对S的速度,利用相对运动速度的关系即可解.解 以地面为参考系,火车相对地面运动的速度为v 1 ,雨滴相对地面竖直下落的速度为v 2 ,旅客看到雨滴下落的速度v 2′为相对速度,它们之间的关系为1'22v v v += (如图所示),于是可得1o12sm 36.575tan -⋅==v v。