梯形的中位线
- 格式:ppt
- 大小:359.00 KB
- 文档页数:12




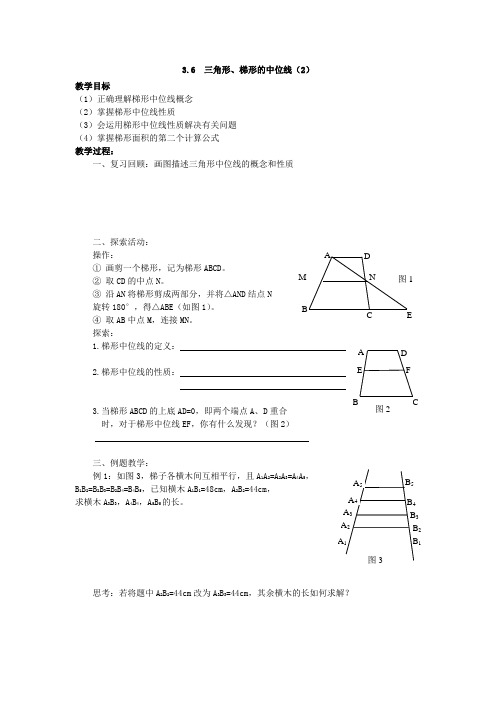
3.6 三角形、梯形的中位线(2)教学目标(1)正确理解梯形中位线概念 (2)掌握梯形中位线性质(3)会运用梯形中位线性质解决有关问题 (4)掌握梯形面积的第二个计算公式 教学过程:一、复习回顾:画图描述三角形中位线的概念和性质二、探索活动:操作: ① 画剪一个梯形,记为梯形ABCD 。
② 取CD 的中点N 。
③ 沿AN 将梯形剪成两部分,并将△AND 结点N 旋转180°,得△ABE (如图1)。
④ 取AB 中点M ,连接MN 。
探索:1.梯形中位线的定义:2.梯形中位线的性质:3.当梯形ABCD 的上底AD=0,即两个端点A 、D 重合时,对于梯形中位线EF ,你有什么发现?(图2)三、例题教学:例1:如图3,梯子各横木间互相平行,且A 1A 2=A 2A 3=A 4A 5,B 1B 2=B 2B 3=B 2B 4=B 4B 5,已知横木A 1B 1=48cm ,A 2B 2=44cm ,求横木A 3B 3,A 4B 4,A 5B 5的长。
思考:若将题中A 2B 2=44cm 改为A 3B 3=44cm ,其余横木的长如何求解?例2:如图4,梯形ABCD 中,AD∥BC,点E 是AB 中点, 连结EC 、ED 、CE ⊥DE ,CD 、AD 与BC 三条线段之间有什么 样的数量关系?请说明理由。
四、练一练(1)梯形的两底长分别为4cm 、6cm ,则中位线的长 。
(2)梯形的一底长6cm,中位线长10cm,则另一底的长 。
(3)若梯形中位线长26cm ,上、下底长度之比为1∶3,,则上底长 cm ,下底长 cm 。
(4)若梯形中位线长14cm ,高5cm ,梯形面积为 cm 2。
由(4)得:S 梯形=21(两底之和)×高 = 五、练习:⑴已知梯形中位线长是5cm ,高是4cm ,则梯形的面积是。
⑵等腰梯形的腰长是6cm ,中位线是5cm ,则梯形的周长是 。
⑶梯形上底与中位线之比是2:5,则梯形下底与中位之比是。

【初中数学】初中数学知识点:梯形,梯形的中位线梯形的定义:一组相对边平行的四边形和另一组相对边不平行的四边形称为梯形。
梯形中平行的两边叫做梯形的底,通常把较短的底叫做上底,较长的底叫做下底,梯形中不平行的两边叫做梯形的腰,梯形的两底的距离叫做梯形的高。
梯形中线:连结梯形两腰的中点的线段。
梯形特性:①梯形的上下两底平行;② 梯形的中线(连接两腰部中点的线称为中线)平行于两个底部,等于上下底部之和的一半。
③等腰梯形对角线相等。
梯形判断:一.一组对边平行,另一组对边不平行的四边形是梯形。
2.一组平行且不相等的四边形为梯形。
梯形中位线定理:梯形中线平行于两个基底,等于两个基底之和的一半。
梯形中位线×高=(上底+下底)×高度=梯形面积梯形中位线到上下底的距离相等中线长度=(上底+下底)梯形的周长和面积:梯形的周长公式为:上底+下底+腰+腰,用字母a+B+C+D表示。
等腰梯形的周长公式:上底+下底+2腰,用字母表示:a+b+2c。
梯形面积公式:(上底+下底)×高÷2,用字母表示:S=(a+b)×h 变形1:h=2s÷(a+b);变形2:a=2S÷H-B;变形3:b=2s÷h-a。
计算梯形面积的另一个公式:中线×高度,用字母表示:l?H对角线互相垂直的梯形面积为:对角线×对角线÷2。
梯形分类:等腰梯形:腰围相等的梯形。
直角梯形:有一个角是直角的梯形。
等腰梯形的特性:(1)等腰梯形的同一底边上的两个角相等。
(2)等腰梯形的对角线相等。
(3)等腰梯形是轴对称图形。
等腰梯形的测定:(1)定义:两腰相等的梯形是等腰梯形(2)定理:在同一基底上有两个相等角度的梯形是等腰梯形(3)对角线相等的梯形是等腰梯形。