函数家族

•Excel函数中最受欢迎的有三大家族，一个是以SUM函数为首的求和家族，一个是以VLOOKUP函数为首的查找引用家族，另外一个就是以IF函数为首的逻辑函数家族。

根据二八定律，学好这三大家族的函数，就能完成80%的工作。

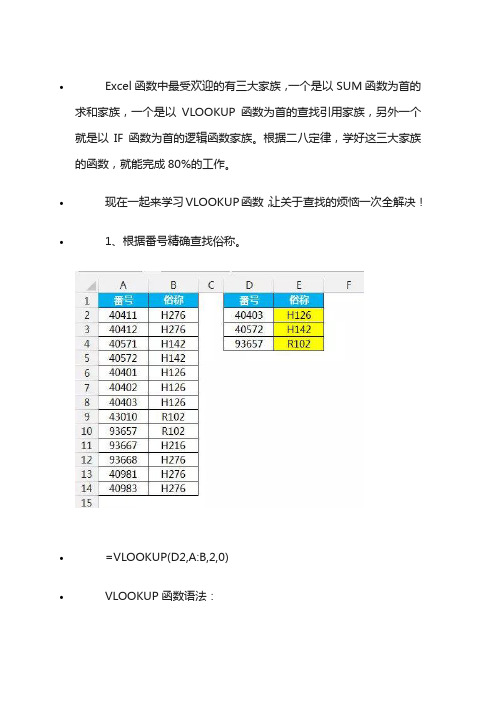
•现在一起来学习VLOOKUP函数，让关于查找的烦恼一次全解决！•1、根据番号精确查找俗称。

•=VLOOKUP(D2,A:B,2,0)•VLOOKUP函数语法：•=VLOOKUP(查找值,查找区域,返回查找区域第N列,查找模式)•VLOOKUP函数示意图。

•2、屏蔽错误值错误值查找。

•=VLOOKUP(D2,A:B,2,0)•VLOOKUP函数如果查找不到对应值会显示错误值#N/A，这个看起来很不美观。

这时可以在外面加个容错函数IFERROR，如果是2013版本那就更好，可以用IFNA函数，这个是专门处理#N/A这种错误值。

•=IFERROR(VLOOKUP(D2,A:B,2,0),"")=IFNA(VLOOKUP(D2,A:B,2,0),"")•函数语法：•=IFERROR(表达式,错误值要显示的结果)•说白了就是将错误值显示成你想要的结果，不是错误值就返回原来的值。

IFNA函数的作用也是一样，只是IFERROR函数是针对所有错误值，而IFNA函数只针对#N/A。

•3、按顺序返回多列对应值。

•通过上面的例子，我们知道可以通过更改第3参数，返回各项对应值如：•=VLOOKUP($A13,$A$1:$F$10,2,0)=VLOOKUP($A13,$A$1:$F$10,3,0)•如果项目少，更改几次参数也没什么，但项目多时，肯定不方便。

如图5-103所示，可以通过ROW、COLUMN产生行列号，从而得到1，2，……，n的值。

•=VLOOKUP($A13,$A$1:$F$10,COLUMN(B1),0)•因为这里是同一行产生序号，所以用COLUMN函数。

arctan(x)和sin(x)的泰勒公式一样1.引言在数学中，泰勒公式是展开一个函数为无穷级数的方法之一。

其中，s i n(x)的泰勒公式是我们常见的公式之一。

然而，你可能会好奇，除了s i n(x)之外，是否还有其他函数拥有类似的泰勒公式呢？本文将介绍a r ct an(x)函数，以及它与s in(x)函数的惊人相似之处。

2. si nus的泰勒公式首先，让我们回顾一下si n(x)函数的泰勒公式。

根据泰勒展开的定义，s i n(x)的泰勒公式可以表示为：$$\s in(x)=x-\f ra c{{x^3}}{{3!}}+\fra c{{x^5}}{{5!}}-\f ra c{{x^7}}{{7!}}+\do ts=\su m_{n=0}^\i nf ty\f ra c{{(-1)^n x^{2n+1}}}{{(2n+1)!}}$$此公式揭示了si n(x)函数可以用一个无穷级数的形式来表示。

它将x的各次幂以及阶乘联系在一起，形成了一个计算s in(x)的有效方法。

3. ar ctanx的泰勒公式a r ct an(x)函数是反三角函数之一，表示求解ta n(x)的逆运算。

让我们来揭开ar ct an(x)函数的泰勒公式之谜。

根据泰勒展开的定义，a r ct an(x)的泰勒公式可以表示为：$$\a rc ta n(x)=x-\fra c{{x^3}}{3}+\fra c{{x^5}}{5}-\f ra c{{x^7}}{7}+\d ot s=\s um_{n=0}^\in ft y\fr ac{{(-1)^n x^{2n+1}}}{{2n+1}}$$正如你所看到的，ar c ta n(x)的泰勒公式与si n(x)的泰勒公式非常相似。

它们具有相同的形式，只是s in(x)的泰勒公式分母为n的阶乘，而a r ct an(x)的泰勒公式分母为2n+1。

4.解释与比较虽然ar ct an(x)和si n(x)的泰勒公式具有相似之处，但它们之间仍存在一些关键差异。

双曲函数shx和chx-概述说明以及解释1.引言1.1 概述概述部分:双曲函数shx和chx是数学中常见的两个双曲函数，它们在数学分析、物理学、工程学等领域都有广泛的应用。

shx和chx函数分别代表双曲正弦函数和双曲余弦函数，在数学上具有类似于正弦函数和余弦函数的性质，但又有着独特的特点和应用价值。

本文将通过对shx和chx函数的介绍和比较，探讨它们在实际应用中的价值和意义。

同时，我们也将展望未来对shx和chx函数研究的方向，以期能够更深入地理解和利用这两个双曲函数。

通过本文的阐述，读者将能够更全面地认识和理解shx和chx函数，并掌握它们在数学和其他学科中的重要作用。

文章结构部分应包括对整篇文章的章节安排和内容概述。

在这一部分，我们将简要介绍文章各个章节的主要内容和论述逻辑，以及各章节之间的衔接关系。

编写如下内容："1.2 文章结构:本文将主要分为引言、正文和结论三大部分。

在引言部分，我们将对双曲函数shx和chx进行概述，介绍文章结构和写作目的。

正文部分将着重讨论shx和chx函数的定义、性质和具体应用，从而探讨它们的优劣势以及可能的发展方向。

最后，在结论部分，我们将通过对shx和chx函数的总结，分析它们在实际应用中的价值，并展望未来的研究方向。

整篇文章将围绕着双曲函数shx和chx展开详细的讨论，旨在为读者提供全面、清晰的认识和理解。

"1.3 目的：本文的主要目的是探讨和比较双曲函数shx和chx的性质、特点和应用。

通过深入分析这两个函数的定义、图像以及与传统三角函数的关系，我们希望读者能更好地理解双曲函数在数学和科学领域的重要性和应用价值。

同时，我们也将讨论shx和chx函数在实际问题中的具体应用，探讨其在工程、物理、经济等领域的实际意义。

通过本文的研究，我们希望为读者提供对双曲函数shx和chx更详细和全面的认识，启发读者对数学问题的新思考和探索。

2.正文2.1 shx函数：shx函数是双曲正弦函数，表示为shx(x)= (e^x - e^(-x))/2。

正弦函数和余弦函数的性质教学与反思正弦函数和余弦函数的性质的教学与学习，一直是数学教学中的一项重要内容。

这是一种基本的数学概念，常被应用于新的科学研究中。

最近，我从事了一项关于正弦函数和余弦函数性质的教学实践，希望从这个实践中学习到一些新的知识，以便更好地为学生提供有价值的教学服务。

一、性质及其应用1.弦函数和余弦函数的性质正弦函数(Sin)和余弦函数(Cos)是经常被引入的函数，它们属于三角函数家族的两个重要成员，它们的性质有：正弦函数的定义域是实数集；余弦函数的定义域也是实数集。

正弦函数的图像关于原点对称，其值域是[-1,1]；余弦函数的图像关于y轴对称，其值域是[-1,1]。

正弦函数和余弦函数在三角函数中具有重要的地位，它们的性质可以被用来推导其它三角函数。

2.用正弦函数和余弦函数的性质在日常的科学研究中有着广泛的应用。

比如，在电动势的研究中，正弦函数可以用来表达负号，这有助于学生理解电动势的变化情况。

在交流电的研究中，正弦波的正弦函数可以精确地描述振荡器的振荡状态，从而更好地理解交流电的性质。

在光学研究中，正弦函数和余弦函数可以用来描述波的变化情况，这对于学生了解各种光现象具有重要的现实意义。

二、实践过程1.学准备在教学准备阶段，我首先准备了一些方面的材料，包括课堂讲稿、教学案例、习题练习等，旨在为学生提供更全面的教学服务。

然后，我就正弦函数和余弦函数的性质进行理论讲解，让学生能够更好地理解此函数性质的规律性。

最后，我准备了一些例题，让学生练习找出正弦函数和余弦函数的性质。

2.学实施在教学实施阶段，我根据学生的学习水平和特点，讲授正弦函数和余弦函数的性质，从理论上介绍了三角函数家族的成员、它们的性质和图像的变化情况。

随后，我利用PowerPoint、视频等教学资料，让学生更直观地感受三角函数的特点。

最后，我准备了一系列的习题，让学生将所学的性质及其应用实践运用起来。

三、反思在这次实践中，我有更深入地了解了正弦函数和余弦函数的性质及其应用，也让学生对它们有了更深刻的理解。

trigonometricfunctions三角函数之歌皓月高照风轻吹，夜色中灵动星汇。

在这宁静的夜晚，我将向你呈现关于三角函数的绚丽歌曲，用1200多个字向你展示三角函数的奇妙之处。

三角函数，数学中的重要角色。

正弦、余弦、正切和它们的倒数，割弦、割割、反正弦、反余弦、反正切，它们呈现出丰富多样的属性。

对于我来说，三角函数是一个神奇的存在，它们与我们生活息息相关。

让我把这些关系与你分享。

首先，我们从最基本的正弦函数开始。

它描绘了一个周期性的波浪形，起起伏伏，曲线连绵不断。

正弦函数是由一个旋转的单位圆而得出的。

令人着迷的是，尽管它只依赖于角度，但它可以在许多不同领域和情境中找到应用。

正弦函数在音乐中扮演着重要的角色。

当你静静地听着美妙的乐曲时，那个优美的旋律正是由正弦函数的震动所产生的。

管弦乐器的弦线的振动、人类声音的波动、乐器的拍子，都可以用正弦函数来描述。

接下来，我们来看看余弦函数。

它与正弦函数非常相似，只是曲线的起点不同。

与正弦函数不同，余弦函数在最高点和最低点出现的时刻恰好是相反的。

余弦函数也在许多领域中发挥着重要作用。

在物理学中，余弦函数通常用于描述振动或波动的行为，比如机械波、光波等。

当受到外力的影响时，物体会发生振动，而余弦函数正是用来描述这种周期性运动的。

此外，在电工领域中，交流电信号也可以通过余弦函数来表示。

我们不能忘记另一位重要的成员，正切函数。

它定义了角度的比率，是一个在数学中非常有效的概念。

正切函数在三角学和几何学中扮演着重要的角色。

在数学中，正切函数常用于解决三角形的问题。

它是沿着直角边与斜边的比值。

通过正切函数，我们可以计算出不可测角以及测量其他角度的长度。

此外，正切函数也在物理学和工程学中广泛应用，比如在力学和电路中。

除了正弦、余弦和正切函数，我们还有一些相关的函数。

例如，割弦函数是正弦函数的倒数，割割函数是余弦函数的倒数。

它们在三角学中能够帮助我们计算以及解决一些特殊问题。

sum函数家族Sum函数家族是一种在Excel中广泛使用的函数类型，它们用于计算一组数字的总和。

在本文中，我们将介绍一些最常用的sum函数，以及它们的特点和用途。

1. Sum函数Sum函数是最基本的sum函数家族成员，它的语法如下：SUM(number1,number2,...)。

这个函数接受一组数字，并将它们相加得到总和。

例如，如果我们想求A1到A5单元格中数字的总和，我们可以这样写：=SUM(A1:A5)。

2. Sumif函数Sumif函数的语法为：SUMIF(range,criteria,sum_range)，它用于根据指定的条件对一组数字进行求和。

例如，如果我们想在A1到A5单元格中，只对大于等于10的数字进行求和，我们可以这样写：=SUMIF(A1:A5,">=10")。

3. Sumifs函数Sumifs函数用于根据多个条件对一组数字进行求和。

它的语法为：SUMIFS(sum_range,criteria_range1,criteria1,criteria_range2,criter ia2,...)，其中sum_range是要进行求和的数字范围，criteria_range1是第一个条件对应的数字范围，criteria1是第一个条件，以此类推。

例如，如果我们想对A1到A5中，颜色为"red"、尺寸为"large"的数字进行求和，我们可以这样写：=SUMIFS(A1:A5,B1:B5,"red",C1:C5,"large")。

4. Sumproduct函数Sumproduct函数用于对两列或多列数字进行求和，并返回乘积之和。

它的语法为：SUMPRODUCT(array1,array2,array3,...)，其中array1、array2、array3等是需要相乘的数字范围。

例如，如果我们想对A1到A5和B1到B5两列数字进行求和，我们可以这样写：=SUMPRODUCT(A1:A5,B1:B5)。

原函数与不定积分的原函数和不定积分是微积分中重要的概念，它们与求导和定积分密切相关。

在这篇文章中，我们将详细解释原函数和不定积分的概念，并探讨它们的性质和应用。

一、原函数的概念原函数是指一个函数的导函数，也就是说，如果函数F的导函数是f，则函数F被称为f的原函数。

可以表示为F'(x)=f(x)。

换句话说，在实数集上，原函数是导数的反函数。

例如，假设f(x)=3x^2，我们可以找到它的一个原函数F(x)=x^3、因为F'(x)=3x^2=f(x)。

在这个例子中，F(x)是f(x)的一个原函数。

原函数的存在性是微积分基本定理的一部分，该定理指出如果f是一个连续函数，则它有一个原函数。

这个定理是微积分的基石之一，为后续的不定积分提供了基础。

二、不定积分的概念不定积分是原函数的一种表示形式，也被称为积分常数。

不定积分是函数的一个反导函数的家族，它表示了在函数的导数中可能缺失的信息。

不定积分的基本性质是线性性质。

如果有两个函数f(x)和g(x)，以及常数a和b，则有以下等式：∫ (a * f(x) + b * g(x)) dx = a * ∫ f(x) dx + b * ∫ g(x)dx这意味着，对于两个函数的线性组合进行不定积分，可以将系数分别提取出来进行计算。

三、不定积分的计算方法计算不定积分的方法有很多种，其中最基本的方法是使用求导的反向运算。

也就是说，我们要找到一个函数F(x)，满足F'(x)=f(x)。

这个过程称为反求导。

常见的不定积分公式包括：1.幂函数积分：∫ x^n dx = (x^(n+1))/(n+1) + C其中n为任意实数，C为积分常数。

2.指数函数积分：∫ e^x dx = e^x + C其中e为自然对数的底数，C为积分常数。

3.三角函数积分：∫ sin(x) dx = -cos(x) + C∫ cos(x) dx = sin(x) + C∫ sec^2(x) dx = tan(x) + C在实际计算中，可以通过对积分公式进行适当的换元和分部积分等方法来简化计算过程。

微积分史The History of Calculus第七讲黎曼内容提要黎曼生平函数的起源对微积分的贡献•黎曼积分•黎曼病态函数•黎曼重排定理其他数学贡献黎曼猜想结语格奥尔格.弗雷德里希.波恩哈德.黎曼(Georg Friedrich Bernhard Riemann) 1826—1866, 德国著名数学家, 物理学家成长经历•黎曼于1826年9月17日出生于汉诺威王国(今德国)的小镇布列斯伦茨(Breselenz). 他的父亲是当地的路德会牧师. •1846年, 黎曼进入哥廷根大学学习哲学和神学. 在此期间他去听了一些数学讲座, 包括高斯(Guass) 关于最小二乘法的讲座. 在得到父亲的允许后, 黎曼改学数学.•1847年春, 黎曼转到柏林大学, 投入雅可比(Jacobi) 、狄利克雷(Dirichlet) 门下, 两年后(1849年)黎曼回到哥廷根在高斯指导下做博士论文, 并于1851年获博士学位.•黎曼是个安静多病而且害羞的人, 终生喜欢独处. 他的同事戴德金(Dedekind) 是少数了解他的人之一. 据戴德金说, 除了黎曼真正糟糕的身体状况之外, 他还是一名疑病症患者.工作经历•1854年, 成为哥廷根大学的讲师•1857年, 黎曼升为哥廷根大学的编外教授•1859年, 黎曼接替狄利克雷成为哥廷根大学的教授•1866年7月20日, 黎曼在第三次去意大利修养的的途中因肺结核在塞拉斯卡(Selasca) 去世, 享年还不到40岁.到了黎曼时代, “ 函数” 已经在分析学占据了举足轻重的位置. 当函数大家族繁衍得越来越复杂、越来越奇特时, 数学家们意识到他们只不过抓到了一只函数概念老虎的尾巴. 17世纪：像牛顿(Newton) 和莱布尼茨(Leibniz) 这样的学者们相信,他们创立的新学科的原始研究材料就是曲线.18世纪中叶：由于欧拉(Euler) 的影响, 人们的注意力从曲线转移到函数, 这一观点的重大转变要从欧拉于1748年出版的《无穷小分析引论》一书开始, 书中把实分析学定位为对函数及其特性的研究. 欧拉首先区分了“ 常量”(始终保持同一个值的量) 和“ 变量” (不确定的或通用的可以取为任何值的量). 然后欧拉提出如下定义:变量的函数是由变量与数值或常量以任何方式构成的解析表达式.19世纪中叶：函数重新出现在现实世界的弦振动和热扩散等问题的研究中. 这里出现了函数演义中的关键人物---傅里叶(Fourier, 1768—1830). 他开始相信-a 和a 之间的任何函数(无论它代表一条弦的位置, 还是一根杆中的热分布, 甚至某种完全“任意”的东西) 都可以表示成我们现在所谓的傅里叶级数:01()(cos sin ),2k k k a k x k x f x a b a aππ∞==++∑其中系数a k 和b k 由下式确定：1()cos ,a k a k x a f x dx a aπ-=⎰1()sin .a k a k x b f x dx a a π-=⎰(1)但并不清楚上边的傅里叶级数中的公式(1)是否总是成立? 系数a k 和b k 为积分式, 如何知道这些积分对一般函数都有意义? 傅里叶在这里至少隐讳地提出了定积分的存在问题, 或函数是否可积的问题. 这些问题由德国数学家狄利克雷(1805—1859) 于1829年提出并开始研究.傅里叶解释他的结果适用于“一个完全任意的函数, 即一组连续的已知值, 不论它们是否服从某个共同的定律”. 狄利克雷是一位才华横溢的数学家, 曾在德国师从高斯, 在法国向傅里叶学习. 他于1829年发表题为《论三角级数的收敛性, 这种级数表示一个介于已知界限之间的任意函数》, 其中讨论了函数用傅里叶级数表示的问题, 以及其中隐含的决定系数的那些积分的存在性问题.狄利克雷提出可用一种比柯西积分新的包容性更强的积分理论来处理区间内有无限多个不连续点的函数(柯西只对于区间[a , b ]上的连续函数定义了积分, 而后将该思想扩展到区间内有有限个不连续点的函数).但他没指出如何对高度不连续的函数积分, 他只给出了这种情况存在的例子, 即现在所说的狄利克雷函数, 可表示为, ()., c x x d x φ⎧=⎨⎩是有理数是无理数(2) 这显然是傅里叶意义下的函数, 但它没有连续点. 这个例子的意义是双重的：一方面表明傅里叶任意函数的思想已经成为处理它的有效方法; 另一方面显示了柯西积分的不足之处. 因此, 应该重建积分的定义, 以免数学家们仅仅局限于对连续函数的积分或对只有有限个不连续点的函数的积分.狄利克雷的学生黎曼接受了重建积分这个挑战, 他试图找到不需要预先假设函数必须如何连续就定义积分的途径. 这是一个大胆的, 极有创见性的思想: 使可积性和连续性分离. 在实分析领域, 黎曼最为杰出的贡献就是, 第一次严格地给出了积分公式---黎曼积分.黎曼作为一名有影响力的数学家, 在实分析、复分析、数论以及微分几何方面做出了持久而革命性的贡献.对微积分的贡献黎曼积分黎曼在1854年为获得哥廷根大学的讲师职位而写的“ 大学执教资格讲演” 这篇论文中, 把这个问题简单地陈述为:“ 如何理解”. 其中假设f (x )在闭区间[a , b ]上有界. ()?b a f x dx黎曼积分黎曼在区间[a, b]内取任意一系列值：a= x0< x1< x2< …< x n－1< x n= b,称之为一个划分. 他将得到的子区间的长度用delta1 = x1－a, delta2 = x2－x1, delta3 = x3－x2, …, delta n= b －x n－1,表示. 再令eps, eps2, eps3, …, eps n为0和1之间的一系列值. 对每个eps k,1x k+ eps k delta k in [x k－1 , x k],然后, 黎曼引入(现在所谓的) 黎曼和(见下图) :S = δ1f (a+ε1δ1) + δ2f (x2+ε2δ2) + … + δn f(x n-1+εnδn),至此, 黎曼给出他的关键定义：如果这个和具有这样的性质：a b x 1X k －1x k δk f (x k －1+eps k delta k )无论怎样选择delta k 和eps k ,当delta k 趋近于无穷小时, 它无限的接近一个固定值A , 那么我们称这个固定的值为().b a f x dx ⎰如果这个和不具备这样的性质, 那么没有意义.()b a f x dx ⎰黎曼积分这是黎曼积分的首次出现. 很明显, 这个定义没有对连续性做任何假设.为了考察可积性, 黎曼引入了新的和：R = delta 1D 1 + delta 2 D 2+ delta 3 D 3+ … +delta n D n , (3)其中D k 为函数f 在区间[x k －1, x k ] 上的“最大振幅”, 即f 在区间[x k －1, x k ] 上的最大值与最小值之差.即R 是如下图(1)所示的阴影区域的面积:a bx 1X k －1x k x 2X n －1delta k D k delta 1D 1delta n D n delta 3D 3图(1)现给定一个正数d > 0 , 黎曼考察区间[a , b ]上所有满足max{delta 1, delta 2,delta 3, …, delta n } 小于等于d 的划分. 即, 他考察那些最宽子区间的长度(即划分的范数) 小于等于d 的划分.黎曼积分然后, 黎曼引入Delta = Delta (d ) 为和式(3) 中范数小于等于d 的划分产生的所有和R 的“最大值” (事实上应为“上确界”).显然, 当且仅当时,黎曼积分0lim ()0d d →∆=() b a f x dx ⎰存在.在几何上, 这意味着当我们越来越细分区间[a , b ]时, 上图中最大阴影区域的面积将减小到0.黎曼积分至此, 黎曼提出了关键性问题：在何种情况下函数可以积分, 在何种情况下函数不能积分?他轻而易举地给出了答案---即现在所说的黎曼可积性条件.黎曼再次给定一个正数sigma > 0. 对于一个给定的划分, 他考察函数在子区间的振幅:称函数振幅大于sigma 的那些子区间为“ A 型” 子区间;而称振幅小于或等于sigma 的子区间为“ B 型”子区间.图(2)sigma a b x 1x 3x 4x 2x 5 黎曼积分图(2)中显示出函数,它的带阴影的那些矩形以及位于左侧的一个sigma 值.最后, 黎曼令s = s (sigma ) 为对于给定sigma 的所有A 型子区间的总长度, 即其中有2个为“ A 型” 子区间[a , x 1], [x 5, b ] 和4个“ B 型”子区间[x 1, x 2], [x 2, x 3], [x 3, x 4], [x 4, x 5].含义：f 可积当且仅当对于无论怎样小的sigma , 我们可以找到这样一个范数, 对于[a , b ]上具有同样小或更小范数的所有划分来说, 函数振幅大于sigma 的子区间的总长度是微不足道的.黎曼可积性条件：存在的充分必要条件是, 对于任意sigma > 0,A 型子区间的总长度s (sigma )在d 0时可以达到任意小. ()baf x dx 黎曼积分黎曼可积性条件的证明过程相对复杂, 但证明思想却很简单:为了使一个函数具有黎曼积分, 它的振幅必须受到限制. 跳变过于频繁过于剧烈的函数是不可积的.由此,黎曼给出了有界函数在[a , b ]上可积的一个充分必要条件.再来考察前边提到的狄利克雷函数. 为明确起见, 我们取c = 1,d = 0,于是有1, ().0, x x x φ⎧=⎨⎩是有理数是无理数黎曼积分问题根据黎曼的定义, 上述狄利克雷函数phi(x )是否可积?假设sigma = 1/2, 考察任意划分0= x 0< x 1< x 2< …<x n －1< x n = 1, 及任意子区间[x k , x k +1],不管这个子区间多么狭窄, 易见phi 在区间[x k , x k +1] 上的振幅为1 －0 > 1/2 = sigma .即划分的每个子区间都是A 型子区间,从而, 对于[0, 1]的任何划分, A 1() 1.2k s δ==∑型根据黎曼可积性条件, 狄利克雷函数不可积!黎曼病态函数直观上, 狄利克雷函数是如此彻底的不连续, 以至于不可积.这个现象提出了一个基本问题:按照黎曼积分的定义, 一个函数不连续到何种程度依然是可积的?这个谜团直到20世纪才解开, 但黎曼本人给出了一个函数,我们称之为黎曼病态函数. 可望提供解决该问题的一个证据.首先, 令(x) = x－n, 其中n是最接近x的整数.例如: (1.2) = (－1.8) = 0.2;(1.7) = (－1.3) = －0.3,如果x 位于两个整数的中间, 如4.5或－0.5, 他置(x) = 0.易见, 函数在每个x = m/2 处具有一个长度为1的跳变不连续性, 其中m是奇自然数. 如下图(3):黎曼接着考察了y =(2x ), 这个函数在水平方向上将图(3)的图形压缩, 产生图(4)的图形, 这时长度为1的跳变出现在x = ＋／－m /4 处, 其中m 是奇自然数.图(3)⋅︒⋅⋅⋅⋅⋅⋅⋅︒︒︒︒︒︒︒1-1-22⋅⋅-111/2y = (x ) 黎曼病态函数这个压缩过程用函数y =(3x ), y =(4x ) 等继续进行下去, 直至黎曼将这些函数组合成一个有趣的函数:图(4)⋅︒⋅⋅⋅⋅⋅⋅⋅︒︒︒1-1-22⋅⋅︒︒︒︒︒︒︒︒︒︒︒︒︒11/21/4⋅y = (2x ) 21()(2)(3)(4)()(),14916k x x x x kx f x k ∞==++++=∑(4) 黎曼病态函数图(5) 画出了函数(4)式在区间[0, 1]上的第7个部分和的图形, 即函数()(2)(3)(4)(5)(6)(7)14916253649x x x x x x x ++++++的图形. 即使在这一步, 也显示了函数f 的不连续性在迅速累积.图(5)黎曼病态函数注意到, 对所有x ,有|(kx )| 小于等于1/2, 运用用比较判别法黎曼在没有给出完整证明的情况下断言:2112k k∞=∑可知这个无穷级数处处收敛.(1) 函数f 在每个单独的函数y = (kx ) 的连续点是连续的,包括所有的无理数;(2) 如果x = m /2n , 其中m 和n 是互素的整数, 那么函数f在x 有一个长度为22211111(1)92549818n n π+++++=的跳变. (这里的级数求和参考欧拉的结果. )黎曼病态函数因此黎曼函数在这样的x = m /2n 处不连续, 而任意两个实数之间存在无限多这种点. 即黎曼函数具有“ 高度不连续性”.然而, 令人惊异的是存在.黎曼借助上面的可积性条件证明了这一点.10()f x dx ⎰任意取定sigma > 0,不妨设sigma = 1/20, 我们要找出振幅超出1/20的那些点.而这种点是形如x = m /2n 的有理数, 且在这种点的跳变幅度是pi 2/8n 2, 所以我们仅需考虑pi 2/8n 2> 1/20,由此推出10 4.967,2n π<≈而n 是正整数, 所以n 只能选择n = 1, 2, 3, 4.对微积分的贡献黎曼病态函数又m 和n 没有公因子, 且0 <<m /2n << 1,黎曼病态函数可推断仅有有限个这样的候选点. 在这种情况下, 函数在区间[0, 1]内的振幅超过1/20的点有11113152357,,,,,,,,,,.86438283468由于仅需处理有限个点, 我们可以建立区间[0, 1]的一个划分, 将这些点中的每一个都置于一个非常狭窄的子区间内,其总长度可以达到任意小. 于是黎曼病态函数可积.这里的关键问题在于振幅超过给定sigma的点为有限个.黎曼将这种情况总结如下:在所有不包含这些跳变点的子区间内, 函数的振幅小于sigma, 并且……包含这些跳变点的子区间的总长度可以随意地小.回忆莱布尼茨级数, 即级数11111.3579-+-+-假定我们按照下述方式重新排列这个级数的项:把第一个负值项排在前面两个正值项的后面; 把第二个负值项排在随后两个正值项的后面, 以此类推.黎曼重排定理在进行三项一组的重排分组后, 我们得到11111111(1)()()539137172111+-++-++-+(5)圆括号内的表达式可以表示为1112411, 1, 2, 3, 4,878341(87)(83)(41)k k k k k k k k -+-==------由于k >= 1, 所以最后这个分数的分子和分母都是正数, 于是, 式(5)中每一个三项分组都是正值. 由此可得关于重排级数的下述结果: 黎曼重排定理11111111(1)()()539137172111+-++-++-+1113(1)0000.86665315≥+-++++==另一方面, 莱布尼茨证明了原来的级数111110.7854.35794π-+-+-=≈即: 通过变更级数中项的位置而不改变其项值就改变了级数的和. 这看起来非常离奇. 事实上, 它的后果更为严重!黎曼证明了莱布尼茨级数竟然可以重排成收敛于任何数值的级数!黎曼重排定理事实上, 对于一般项级数(包含正项与负项)1, kn u∞=∑黎曼的老师狄利克雷证明了一个绝对收敛级数的任何重排必定收敛于原来级数的同一个和. 即对于绝对收敛级数, 重排它的项不会对和产生任何影响.而对于条件收敛级数, 黎曼证明可以把它重排为收敛于我们希望的任意值.这就是“黎曼惊人的重排结果”.黎曼重排定理黎曼的证明思想:令C是一个固定数(不妨设C为一个正数)---可以说是“靶子”.黎曼这样开始: “以交替的方式, 首先取级数足够多的正值项使其和超过C, 然后取足够多的负值项使总和小于C.”.一直重复这一过程. 可以证明用这种交替方案进行的重排级数将收敛于C.为了说明起见, 下面假定我们寻找莱布尼茨级数的一个重排使之收敛于1.10.(3) 然后再加上某些正值项使其和超过1.10, 再减去某些负值项使其差小于1.10,以此类推. 得莱布尼茨级数如下:黎曼重排定理11111111111(1)()()539131772125293311+-+++-++++-+黎曼的级数重排定理证明了无穷求和是一个微妙的问题. 这再一次印证了: 无穷过程的研究或分析, 可能使我们陷入困境!(1) 先找出足够多的正值项使其和超过1.10:1 + 1/5 = 1.2 > 1.10;(2) 接着减去一个负值项使其差小于1.10:1 + 1/5 -1/3 = 0.8666… < 1.10;其他数学贡献复分析黎曼在复分析领域, 最为杰出的贡献是黎曼曲面的引入, 以及对于复分析的自然的几何处理.•1851年, 黎曼的博士论文即为《单复变函数一般理论基础》, 得到高斯的赞赏, 高斯以少有的激情给黎曼写下了评语: “黎曼先生提交的博士论文提供了可信的证据, 表明作者对他的论文所涉及的主题进行了全面、深入的研究,显示了一个具有创造力的、活跃的、真正数学的头脑以及了不起的富有成果的独创性.”•其中论证了复变函数可导的必要充分条件(即柯西-黎曼方程) , 借助狄利克雷原理阐述了黎曼映射定理, 成为函数的几何理论的基础.其他数学贡献微分几何黎曼对微分几何开创性的贡献奠定了广义相对论的基础.•1854年, 黎曼作了题为《论作为几何基础的假设》的演讲, 发扬了高斯关于曲面的微分几何研究, 提出用流形的概念理解空间的实质, 用微分弧长度的平方所确定的正定二次型理解度量, 建立了黎曼空间的概念, 开创了黎曼几何, 把欧氏几何、非欧几何包括进他的体系之中, 为爱因斯坦的广义相对论提供了数学基础;•1857年, 黎曼发表了关于阿贝尔函数的研究论文, 引出黎曼曲面的概念, 将阿贝尔积分与阿贝尔函数的理论带到新的转折点并做系统的研究, 其中对黎曼曲面从拓扑、分析、代数几何各角度作了深入研究, 创造了一系列对代数拓扑发展影响深远的概念, 阐明了后来为G.罗赫所补足的黎曼-罗赫定理.黎曼猜想•1859年, 黎曼被选为了柏林科学院的通信院士. 作为对这一崇高荣誉的回报, 黎曼向柏林科学院提交了一篇题为《不超过已知数的素数的数量》只有短短八页的论文. 这篇论文就是黎曼猜想的“ 诞生地”, 被公认为是解析数论领域最有影响力的论文.•黎曼猜想要解决的问题是黎曼zeta函数ζ(s)的非平凡零点都位于复平面Re(s)=1/2直线上. 数学家们把这条直线称为临界线. 运用这一术语, 黎曼猜想可以表述为：黎曼ζ(s)函数的所有非平凡零点都位于临界线上.•黎曼猜想是希尔伯特(Hilbert) 在1900年提出的二十三个问题的第八问题, 现在又被列为千禧年七大难题之一.黎曼猜想黎曼猜想•有人曾经问希尔伯特: “如果500年后能重回人间, 他最希望了解的事情是什么?”希尔伯特回答说：“我想知道, 黎曼猜想解决了没有.”•美国数学家蒙哥马利(Montgomery) 曾经也表示, 如果有魔鬼答应让数学家们用自己的灵魂来换取一个数学命题的证明, 多数数学家想要换取的将会是黎曼猜想的证明.•2018年9月, 菲尔茨奖和阿贝尔奖双料得主, 89岁高龄的迈克尔·阿蒂亚(Michael Atiyah)声称自己证明了黎曼猜想, 他于9月24日在海德堡获奖者论坛上宣讲了他的证明, 同时贴出了他证明黎曼猜想的预印本. 但阿蒂亚的证明有不少疑点, 尚待考证.结语黎曼在他短暂的一生中, 对于几何、分析和物理学的众多领域都作了开创性的贡献. 他耗尽毕生心血为我们创造了崭新的概念和强有力的方法. 有数学家评论说:“黎曼是一个富有想象力的天才, 他的想法即使没有证明, 也鼓舞了整整一个世纪的数学家”.大数学家冯.诺依曼(Von Neumann) 说: “ 黎曼的科学个性是数学的两重性的光辉榜样”.黎曼给我们的启示任何创新的道路上都没有坦途, 都不是一帆风顺, 但做科学研究要敢于大胆假设, 小心求证.谢谢观看Thanks参考文献1.《微积分的历程：从牛顿到勒贝格》, William Dunham著, 李伯民, 汪军, 张怀勇译, 北京：人民邮电出版社, 2010.2.《天才引导的历程---数学中的伟大定理》, William Dunham著, 李繁荣, 李莉萍译, 北京：机械工业出版社, 2013.3.《数学史》, Carl. B. Boyer著, Uta C.Merzbach修订, 秦传安译, 北京：中央编译出版社, 2012.4.《古今数学思想》, Morris Kline著, 邓东皋, 张恭庆等译, 上海：上海科学技术出版社,2014.5.《数学恩仇录---数学家的十大论战》, Hal Hellman著, 范伟译, 上海：复旦大学出版社,2009.6.《数学星空中的璀璨群星》, 易南轩, 王芝平编著, 北京：科学出版社, 2009.7.《文明之光---图说数学史》, 李文林主编, 山东教育出版社, 2005.8.《大数学家---从阿基米德到陈省身》, 陈诗谷, 葛孟曾著, 北京：中国青年出版社, 2012.9.《三次数学危机与数学悖论》, 韩雪涛著, 北京：人民邮电出版社, 2016.10.《数学史概论》(第三版), 李文林, 北京：高等教育出版社, 2010.11.《微积分的创立者及其先驱》(第3版), 李心灿编, 北京：高等教育出版社, 2007.12.《数学精英》, Bell. E. T. 著, 徐源译, 北京：商务印书馆, 1991.13.百度百科(部分图片来源于百度百科).。

正切余切正割余割在数学的三角函数世界里，正切、余切、正割、余割是四个重要的概念。

它们在解决几何问题、物理问题以及工程应用中都发挥着关键的作用。

咱们先来聊聊正切。

正切用符号“tan”表示，它是一个角的对边与邻边的比值。

简单来说，如果我们有一个直角三角形，一个锐角所对应的对边长度为 a，邻边长度为 b，那么这个角的正切值就是 a/b。

比如说，一个角的对边是 3，邻边是 4，那这个角的正切值就是 3/4。

正切函数的图像可是很有特点的。

它的定义域是整个实数集，但要除去一些特殊的点，比如π/2 ＋kπ（k 是整数），因为在这些点上，正切函数是没有定义的。

正切函数的图像在定义域内是周期性的，周期是π。

而且，它的图像在不同的区间内呈现出不同的增减性。

接着说说余切。

余切用“cot”表示，它是邻边与对边的比值。

还是用刚才那个直角三角形举例，如果对边是 a，邻边是 b，那这个角的余切值就是 b/a。

余切函数的定义域也是除去一些特殊点的实数集，它的周期同样是π。

正切和余切之间有着密切的关系。

它们互为倒数，也就是说tanα × cotα ＝ 1。

这一关系在解决很多数学问题时都能派上用场。

再来讲讲正割。

正割用“sec”表示，它是斜边与邻边的比值。

对于那个直角三角形，斜边长度是 c，邻边长度是 b，那么这个角的正割值就是 c/b。

正割函数的定义域也是除去一些特殊点的实数集。

余割呢，用“csc”表示，是斜边与对边的比值。

在同一个直角三角形中，如果斜边是 c，对边是 a，那么这个角的余割值就是 c/a。

正割和余割之间也存在类似正切和余切的关系，那就是secα × cscα＝ 1。

在实际应用中，正切、余切、正割、余割都非常有用。

比如在物理学中，研究波动现象、交流电等问题时，经常会用到这些三角函数。

在工程领域，计算建筑物的倾斜度、桥梁的受力分析等，也离不开它们。

咱们通过一个具体的例子来感受一下。

假设要计算一个斜坡的坡度，我们就可以用正切来表示。