茎叶图例题配置说课
- 格式:ppt
- 大小:152.50 KB
- 文档页数:13

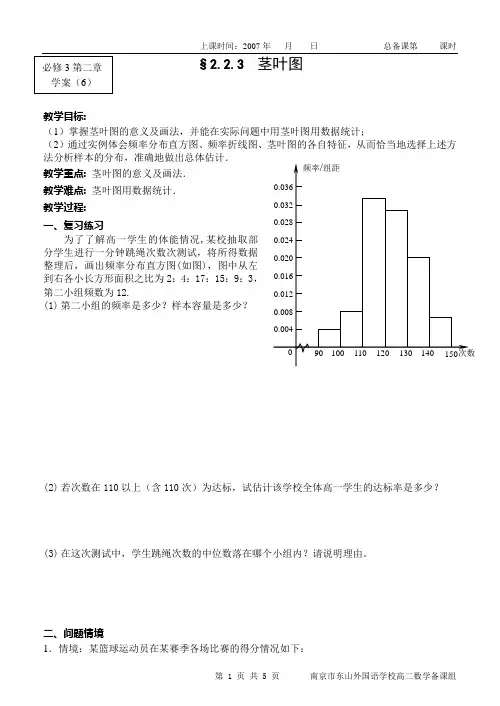
教学目标:(1)掌握茎叶图的意义及画法,并能在实际问题中用茎叶图用数据统计;(2)通过实例体会频率分布直方图、频率折线图、茎叶图的各自特征,从而恰当地选择上述方法分析样本的分布,准确地做出总体估计.教学重点:茎叶图的意义及画法.教学难点:茎叶图用数据统计.教学过程:一、复习练习为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数次测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.(1)第二小组的频率是多少?样本容量是多少?(2)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?(3)在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由。
二、问题情境1.情境:某篮球运动员在某赛季各场比赛的得分情况如下:12,15,24,25,31,31,36,36,37,39,44,49,50.2.问题:如何有条理地列出这些数据,分析该运动员的整体水平及发挥的稳定程度?三、建构数学1.茎叶图的概念:_______________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________2.茎叶图的特征:_______________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________四、数学运用1.例题:例1.(1)情境中的运动员得分的茎叶图如图:(2)从这个图可以直观的看出该运动员平均得分及中位数、众数都在20和40之间,且分布较对称,集中程度高,说明其发挥比较稳定.例2.甲、乙两篮球运动员在上赛季每场比赛的得分如下,试比较这两位运动员的得分水平.甲 12,15,24,25,31,31,36,36,37,39,44,49,50.乙8,13,14,16,23,26,28,33,38,39,512.练习:(1)右面是甲、乙两名运动员某赛季一些场次得分的茎叶图,据图可知()A.甲运动员的成绩好于乙运动员B.乙运动员的成绩好于甲运动员C.甲、乙两名运动员的成绩没有明显的差异D.甲运动员的最低得分为0分(2)课本第58页,练习第1题.五、回顾小结:1.绘制茎叶图的一般方法;2.茎叶图的特征.六、课外作业:课本第60页第7、8、9题.甲12345乙824719936250328754219441练习1、在某电脑杂志的一篇文章中,每个句子的字数如下:10,28,31,17,23,27,18,15,26,24,20,19,36,27,14,25,15,22,11,24,27,17。


2.2.3茎叶图教学目标:1.掌握茎叶图的意义及画法,并能在实际问题中用茎叶图用数据统计;2.通过实例体会频率分布直方图、频率折线图、茎叶图的各自特征,从而恰当地选择上述方法分析样本的分布,准确地做出总体估计.教学重点:茎叶图的意义及画法.教学难点:用茎叶图进行数据统计.教学方法:1.通过组织学生观察茎叶图特点,用图形直观的方法引出茎叶图的概念,有利于学生对概念的了解.2.通过本课的学习,使学生进一步体会观察、比较、归纳、分析等一般科学方法的运用.教学过程:一、问题情境情境:某篮球运动员在某赛季各场比赛的得分情况如下:12,15,24,25,31,31,36,36,37,39,44,49,50.二、学生活动如何有条理地列出这些数据,分析该运动员的整体水平及发挥的稳定程度?三、建构数学1.茎叶图的概念:一般地:当数据是一位和两位有效数字时,用中间的数字表示十位数,即第一个有效数字,两边的数字表示个位数,即第二个有效数字,它的中间部分像植物的茎,两边部分像植物茎上长出来的叶子,因此通常把这样的图叫做茎叶图.茎按从小到大的顺序从上向下列出,共茎的叶一般按从大到小(或从小到大)的顺序同行列出.2.茎叶图的特征:(1)用茎叶图表示数据有两个优点:一是从统计图上没有原始数据信息的损失,所有数据信息都可以从茎叶图中得到;二是茎叶图中的数据可以随时记录,随时添加,方便记录与表示;(2)茎叶图只便于表示两位(或一位)有效数字的数据,对位数多的数据不太容易操作;而且茎叶图只方便记录两组的数据,两个以上的数据虽然能够记录,但是没有表示两个记录那么直观,清晰;(3)茎叶图对重复出现的数据要重复记录,不能遗漏四、数学运用1.例题.例1 (1)情境中的运动员得分的茎叶图如图: (2)从这个图可以直观的看出该运动员平均得分及中位数、众数都在20和40之间,且分布较对称,集中程度高,说明其发挥比较稳定.例2 甲、乙两篮球运动员在上赛季每场比赛的得分如下,试比较这两位运动员的得分水平.甲 12,15,24,25,31,31,36,36,37,39, 44,49,50. 乙 8,13,14,16,23,26,28,33,38,39,51 解:画出两人得分的茎叶图.2.练习:(1) 右面是甲、乙两名运动员某赛季一些场次得分的茎叶图,据图可知 ( A )A .甲运动员的成绩好于乙运动员B .乙运动员的成绩好于甲运动员C .甲、乙两名运动员的成绩没有明显的差异D .甲运动员的最低得分为0分 (2)课本第61页练习第1,3题. 五、要点归纳与方法小结 1.绘制茎叶图的一般方法;甲 0 1 2 3 4 5 乙 8 247 199 36 25032 875421 944 12.茎叶图的特征.。






茎叶图一.茎叶1.茎叶:茎按从小到大的序从上向下列出,共茎的叶一般按从大到小( 或从小到大 ) 的序同行列出。
2.茎叶的特征(1)用茎叶表示数据有两个点:一是上没有原始数据信息的失,所有数据信息都可以从茎叶中得到;二是茎叶中的数据可以随,随添加,方便与表示。
(2)茎叶只便于表示两位有效数字的数据,而且茎叶只方便两的数据,两以上的数据然能,但是没有表示两个那么直、清晰。
当本数据多,因每一个数据都要在中占据一个空,用茎叶很不方便。
3.制作茎叶图的方法是:将所有两位数的十位数字作为“茎”,个位数字作为“叶”,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出,共茎的叶一般按从大到小(或从小到大)的顺序同行列出.茎叶图对于分布在0~99 的容量较小的数据比较合适,此时,茎叶图比直方图更详尽地表示原始数据的信息 .在茎叶图中,茎也可以放两位,后面位数多可以四舍五入后再制图.4.画茎叶的注意事(1)将每个数据分茎(高位)和叶(低位)两部分,当数据是两位整数,茎十位上的数字,叶个位上的数字;当数据是由整数部分和小数部分成,可以把整数部分作茎,小数部分作叶。
(2)将茎上的数字按大小次序排成一列。
(3)了方便分析数据,通常将各数据的叶按大小次序写在其茎右(左)。
(4)用茎叶比数据,一般从数据分布的称性、中位数,定性等方面来比。
二.茎叶中常用的几个量:众数. 中位数 . 平均数(本的数字特征)(1)众数:出次数最多的数叫做众数.(2)中位数:如果将一数据按大小序依次排列,把在最中位置的一个数据或中两个数据的平均是叫做数据的中位数. ( 例: 2、 3、 4、 5、 6、 7中位数:( 4+5)/2= (例: 1、 2、 3、 6、 7的中位数是 3。
)xn叫做(3)平均数与加平均数:如果有n 个数1,2,x 3,xn,那么xx1x2nx xn个数的平均数 . 如果在 n 个数中 , 11次 ,x22次 ,k2次,x出次 f出次 f⋯⋯,x出次 f(里 f1 f2f k n),那么x1( x1 f1x2 f2x k f k ) 叫做n个数的加平均n数,其中 f1,f 2, f k叫做.( 4)准差与方差:一数据x1, x2, x3的平均数x,, x n,ss2( x1 x)2(x2x) 2( x n x)2,其中s2 表示方差,s表示准差.n例 1 下面一数据是某生 30 名工人某日加工零件的个数,适当的茎叶表示数据,并由出明一下个此日的生情况。
2。
2.3茎叶图整体设计教材分析通过比较甲、乙两个运动员比赛得分情况引入茎叶图,从而得出画茎叶图的步骤,从茎叶图中的枝叶分布情况就可以感受到样本数据的分布特点。
结合实例说明,可根据数据的特点灵活地决定茎叶图中数据的茎和叶的划分.茎叶图,频率分布表和频率分布直方图都是用来描述样本数据的分布情况的。
茎叶图由所有样本数据构成,没有损失任何样本信息,可以在抽样的过程中随时记录;而频率分布表和频率分布直方图则损失了样本的一些信息,必须在完成抽样后才能制作.三维目标1。
通过实例使学生掌握茎叶图的意义及画法,体会分布的意义和作用,在表示样本数据的过程中,进一步学会列频率分布表及画频率分布直方图、频率折线图、茎叶图,体会它们各自的特点.2。
使学生进一步体会用样本估计总体的思想,会用样本的频率分布估计总体分布。
重点难点教学重点:1。
使学生掌握茎叶图的意义及画法,结合实例体会茎叶图的优点;2.继续掌握如何用样本频率分布估计总体分布。
教学难点:对频率分布直方图的理解和应用.课时安排1课时教学过程导入新课设计思路一:(复习导入)一般地,对于n 个数x 1,x 2,…,x n ,我们把n n x x x n +++...21叫做这n个数的算术平均数,简称平均数。
平均数常用于表示一组数据的平均水平。
计算平均数时,所有数据都参加运算,它能充分利用数据所描述的信息,因此在生活中较为常见,但它易受端点值的影响。
一般地,n 个数根据大小顺序排列后,处于中间位置的一个数据(或中间两个数据的平均数)叫做这组数据的中位数。
由中位数的定义可知,当数据的个数是奇数时最中间的一个数据是中位数;当数据的个数是偶数时,则最中间两个数据的平均数是中位数.中位数受端点值的影响小,但不能充分利用所有数据的信息.众数则是一组数据中出现次数最多的那个数据.为了避开以上缺点,今天学习——茎叶图.因为所有信息都可以从茎叶图中得到体现。
设计思路二:(事例导入)某篮球运动员某赛季各场比赛的得分情况如下:12,15,24,25,31,31,36,36,37,39,44,49,50.如何分析该运动员的整体水平及发挥的稳定程度?推进新课新知探究除了前几天学的图、表以及上面的各种数能帮助我们分析数据外,统计中还有一种用来表示数据的茎叶图(stem and leaf display).顾名思义,茎是指中间的一列数,叶就是指从茎的两旁生长出来的数,中间的数字表示得分的十位数,旁边的数字分别表示两名运动员得分的个位数,像这样用来表示数据,帮助我们理解样本数据的图,我们称为茎叶图.制作茎叶图的方法是:当所给数据为一位数时,可将0作为茎叶较长的茎,而它本身作为叶;当所给数据为两位数时,将所有两位数的十位数字作为“茎”,个位数字作为“叶”;当所给的数据为三位数时,可将百位和十位作为“茎”,而个位数字作为“叶”.茎相同的数据共用一个茎,茎按从小到大的顺序从上到下排列,共用茎的叶一般要按从大到小(也可以从小到大)的顺序同行排出.制作茎叶图时,一般用一个竖线将茎叶隔开,竖线的左边是茎,右边是叶。
茎叶图教学目标(1)掌握茎叶图的意义及画法,并能在实际问题中用茎叶图用数据统计;(2)通过实例体会频率分布直方图、频率折线图、茎叶图的各自特征,从而恰当地选择上述方法分析样本的分布,准确地做出总体估计.教学重点茎叶图的意义及画法.教学难点茎叶图用数据统计.教学过程一、复习练习:为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数次测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12. (1)第二小组的频率是多少?样本容量是多少? (2)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?(3)在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由。
分析:在频率分布直方图中,各小长方形的面积等于相应各组的频率,小长方形的高与频数成正比,各组频数之和等于样本容量,频率之和等于1。
解:(1)由于频率分布直方图以面积的形式反映了数据落在各小组内的频率大小, 因此第二小组的频率为:40.0824171593=+++++ 又因为频率=第二小组频数样本容量所以 121500.08===第二小组频数样本容量第二小组频率 (2)由图可估计该学校高一学生的达标率约为171593100%88%24171593+++⨯=+++++ (3)由已知可得各小组的频数依次为6,12,51,45,27,9,所以前三组的频数之和为69,前四组的频数之和为114,所以跳绳次数的中位数落在第四小组.二、问题情境1.情境:某篮球运动员在某赛季各场比赛的得分情况如下:12,15,24,25,31,31,36,36,37,39,44,49,50.2.问题:如何有条理地列出这些数据,分析该运动员的整体水平及发挥的稳定程度?三、建构数学1.茎叶图的概念:一般地:当数据是一位和两位有效数字时,用中间的数字表示十位数,即第一个有效数字,两边的数字表示个位数,即第二个有效数字,它的中间部分像植物的茎,两边部分像植物茎上长出来的叶子,因此通常把这样的图叫做茎叶图。
江苏省徐州市高中数学2.2.3 茎叶图教案苏教版必修3编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(江苏省徐州市高中数学2.2.3 茎叶图教案苏教版必修3)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为江苏省徐州市高中数学2.2.3 茎叶图教案苏教版必修3的全部内容。
茎叶图教学目标是学生掌握茎叶图的意义及画法,并能在实际问题中用茎叶图进行数据统计教学重难点要能够通过茎叶图,分析单组数据,以及比较两组数据的差异教学参考书教参授课方法讲练结合教学辅助手段多媒体专用教室教学教学二次备课过程设计新课学习案例:某篮球运动员在某赛季各场比赛的得分情况如下:12,15,24,25,31,31,36,36,37,39,44,49,50.如何分析该运动员的整体水平及发挥的稳定程度.分析:1、上节课我们介绍了频率分布表,频率分布直方图帮助我们分析数据。
我们还有一种简易的方法,就是将这些数据有条理地列出来,从中观察数据的分布情况.这种方法就是画出该运动员得分的茎叶图.【精典范例】甲、乙两篮球运动员上赛季每场比赛的得分如下,试比较这两位运动员的得分水平甲:12,15,24,25,31,31,36,36,37,39,44,49,50乙:8,13,14,16,23,26,28,33,38,39,51【解】画出两人得分的茎叶图,为便于对比分析,可将茎放在中间共用,叶分别列左、右两侧:从这个茎叶图可以看出:1、甲运动员2、乙运动员3、甲、乙比较课前准备:仔细阅读课本P60--612、制作茎叶图的方法是:将所有两位数的十位数字作为“茎”,个位数字作为“叶”,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出,共茎的叶一般按从大到小(或从小到大)的顺序同行列出.茎叶图:3、从茎叶图可以粗略地看出,该运动员平均得分及中位数、众数都在20到40之间,且分布较对称,集中程度高,说明其发挥比较稳定.教学教学二次备课过程设计当堂训练:1、一球员在NBA某些场次的比赛所得篮板球数分别为,请制作这些数据的茎叶图166351219149710121486101010761110129151581361031091161111139105121741281213188162.下面是甲、乙两名运动员某赛季一些场次得分的茎叶图:甲乙0 850 1 24732 2 199875421 3 36944 41 5 2(1)甲、乙两名队员的最高得分各是多少?(2)哪名运动员的成绩好一些?课堂小结:1、茎叶图画法2、茎叶图的意义【小结】1、茎叶图的优点在于保持数据无损的情况下较为直观地反映数据分布特征,对两位数(或只有末两位不同的多位数)的数据表示很方便,缺点在于多位数的表示不太方便、直观.2、.茎叶图可用于展示原始数据的分布,同时还保留原始数据在图形里面,相当直观.从茎叶图中,可直接看出数据是否对称、是否有极端值以及数据的集中趋势和离中趋势.3、茎叶图可以分析单组数据,也能对两组数据进行比较,画出两组数据的茎叶图,可将茎放在中间共用,叶分列左、右两侧,左侧的叶按从大到小的顺序写,右侧的叶按从小到大的顺序。
茎叶图一.茎叶图1.茎叶图:茎按从小到大的顺序从上向下列出,共茎的叶一般按从大到小(或从小到大)的顺序同行列出。
2.茎叶图的特征(1)用茎叶图表示数据有两个优点:一是统计图上没有原始数据信息的损失,所有数据信息都可以从茎叶图中得到;二是茎叶图中的数据可以随时记录,随时添加,方便记录与表示。
(2)茎叶图只便于表示两位有效数字的数据,而且茎叶图只方便记录两组的数据,两组以上的数据虽然能够记录,但是没有表示两个记录那么直观、清晰。
当样本数据较多时,因为每一个数据都要在图中占据一个空间,用茎叶图很不方便。
3.制作茎叶图的方法是:将所有两位数的十位数字作为“茎”,个位数字作为“叶”,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出,共茎的叶一般按从大到小(或从小到大)的顺序同行列出.茎叶图对于分布在0~99的容量较小的数据比较合适,此时,茎叶图比直方图更详尽地表示原始数据的信息. 在茎叶图中,茎也可以放两位,后面位数多可以四舍五入后再制图.4.画茎叶图时的注意事项(1)将每个数据分为茎(高位)和叶(低位)两部分,当数据是两位整数时,茎为十位上的数字,叶为个位上的数字;当数据是由整数部分和小数部分组成时,可以把整数部分作为茎,小数部分作为叶。
(2)将茎上的数字按大小次序排成一列。
(3)为了方便分析数据,通常将各数据的叶按大小次序写在其茎右(左)侧。
(4)用茎叶图比较数据时,一般从数据分布的对称性、中位数,稳定性等方面来比较。
二.茎叶图中常用的几个量:众数.中位数.平均数(样本的数字特征) (1)众数:出现次数最多的数叫做众数.(2)中位数:如果将一组数据按大小顺序依次排列,把处在最中间位置的一个数据或中间两个数据的平均是叫做这组数据的中位数. (例:2、3、4、5、6、7 中位数:(4+5)/2= (例:1、2、3、6、7的中位数是3。
)(3)平均数与加权平均数:如果有n 个数,,,,n x x x x ⋯⋯321那么12nx x x x n++⋅⋅⋅+=叫做这n个数的平均数. 如果在n 个数中,1x 出现次1f 次, 2x 出现次2f 次,……,k x 出现次2f 次,(这里),n f f f k =+⋯⋯++21那么11221()k k x x f x f x f n =++⋅⋅⋅+叫做这n 个数的加权平均数,其中k f f f ⋯⋯,,21叫做权.(4)标准差与方差:设一组数据123nx x x x ⋯,,,,的平均数为x ,则nx x x x x x s s n 222212)()()(-++-+-==Λ,其中2s 表示方差,s 表示标准差. 例1 下面一组数据是某生产车间30名工人某日加工零件的个数,请设计适当的茎叶图表示这组数据,并由图出发说明一下这个车间此日的生产情况。