新课标九年级数学竞赛辅导讲座 第一讲 走进追问求根公式【教案】
- 格式:doc
- 大小:516.01 KB
- 文档页数:5

新课标九年级数学竞赛培训第01讲:求根公式© 2011 菁优网一、填空题(共7小题,每小题3分,满分21分)1、满足(n2﹣n﹣1)n+2=1的整数n有_________个.2、已知a,b为实数,且+|b﹣|=0,则关于x的方程(a+2)x2+b2=a﹣1的解为_________.3、(2001•四川)若x2﹣3x﹣2=0,则=_________.4、已知x2+xy+y=14①,y2+xy+x=28②,则x+y的值为_________.5、若x2﹣5x+1=0,则=_________.6、已知m、n是有理数,方程x2+mx+n=0有一个根是,则m+n的值为_________.7、已知a是方程x2﹣x﹣2000=0的一个正根.则代数式的值为_________.二、选择题(共7小题,每小题3分,满分21分)8、设x1、x2是二次方程x2+x﹣3=0的两个根,那么x13﹣4x22+19的值等于()A、﹣4B、8C、6D、09、若两个方程x2+ax+b=0和x2+bx+a=0只有一个公共根,则()A、a=bB、a+b=0C、a+b=1D、a+b=﹣110、当分式有意义时,x的取值范围是()A、x<﹣1B、x>4C、﹣1<x<4D、x≠﹣1且x≠411、方程(x+1)|x+1|﹣x|x|+1=0的实根的个数是()A、0B、1C、2D、312、对于方程x2﹣2|x|+2=m,如果方程实根的个数恰为3个,则m值等于()A、1B、2C、D、2.513、自然数n满足,这样的n的个数是()A、2B、1C、3D、414、设a,b都是正实数且,那么的值为()A、B、C、D、三、解答题(共11小题,满分73分)15、是否存在某个实数m,使得方程x2+mx+2=0和x2+2x+m=0有且只有一个公共的实根?如果存在,求出这个实数m及两方程的公共实根;如果不存在,请说明理由.16、解关于x的方程(p+1)x2﹣2px+p﹣2=0.17、设方程x2﹣|2x﹣1|﹣4=0,求满足该方程的所有根之和.18、已知实数a、b、c、d互不相等,且,试求x的值.19、解下列关于x的方程:(1)(m﹣1)x2+(2m﹣1)x+m﹣3=0;(2)x2﹣|x|﹣1=0;(3)|x2+4x﹣5|=6﹣2x.20、(2003•上海)已知x2﹣2x=2,求代数式(x﹣1)2+(x+3)(x﹣3)+(x﹣3)(x﹣1)的值.21、已知,求的值.22、已知m、n是方程x2+2003x+7=0的两根,求(m2+2002m+6)(n2+2004n+8)的值.23、在一个面积为l的正方形中构造一个如下的小正方形:将正方形的各边n等分,然后将每个顶点和它相对顶点最近的分点连接起来,如图所示,若小正方形面积为,求n的值.24、已知方程x2﹣3x+1=0的两根α、β也是方程x4﹣px2+q=0的根,求p、q的值.25、如图,锐角△ABC中,PQRS是△ABC的内接矩形,且S△ABC=nS矩形PQRS,其中n为不小于3的自然数.求证:需为无理数.答案与评分标准一、填空题(共7小题,每小题3分,满分21分)1、满足(n2﹣n﹣1)n+2=1的整数n有4个.考点:负整数指数幂。

第一讲走进追问求根公式形如 ax2bx c0 ( a0 )的方程叫一元二次方程,配方法、公式法、因式分解法是解一元二次方程的基本方法。
而公式法是解一元二次方程的最广泛、最拥有一般性的方法。
求根公式 x1,2bb 24ac内涵丰富:它包括了初中阶段已学过的所有代数运算;它回答了一元2a二次方程的诸如如何务实根、实根的个数、何时有实根等基本问题;它展现了数学的简短美。
降次转变是解方程的基本思想,有些条件中含有 (或可转变为 )一元二次方程有关的问题,直接求解可能给解题带来很多不便,常常不是去解这个二次方程,而是对方程进行适合的变形来代换,进而使问题易于解决。
解题经常用到变形降次、整体代入、结构零值多项式等技巧与方法。
【例题求解】【例 1】知足(n2n 1)n2 1 的整数n有个。
思路点拨:从指数运算律、± 1 的特点人手,将问题转变为解方程。
【例 2】设 x1、 x2是二次方程 x2x 30 的两个根,那么x13 4 x2219的值等于()A、一 4 B 、8C、 6D、 0思路点拨:求出 x1、 x2的值再代入计算,则计算繁难,解题的重点是利用根的定义及变形,使多项式降次,如 x123x1, x223x2。
【例 3】解对于x的方程(a1) x 22ax a 0 。
思路点拨:因不了解原方程的种类,故需分 a 10及 a10 两种状况议论。
【例 4】设方程 x22x140 ,求知足该方程的所有根之和。
思路点拨:经过议论,脱去绝对值符号,把绝对值方程转变为一般的一元二次方程求解。
【例 5 】已知实数 a 、b、 c 、d互不相等,且a 1b11d1试求 x 的值。
b cc x ,d a思路点拨:运用连等式,经过迭代把 b 、c、 d 用a的代数式表示,由解方程求得x 的值。
注:一元二次方程常有的变形形式有:(1)把方程 ax2bx c0 ( a0 )直接作零值多项式代换;(2)把方程 ax2bx c0 ( a0 )变形为 ax 2bx c ,代换后降次;(3)把方程 ax2bx c0( a0 )变形为 ax 2bx c 或 ax2c bx ,代换后使之转变关系或整体地消去 x 。

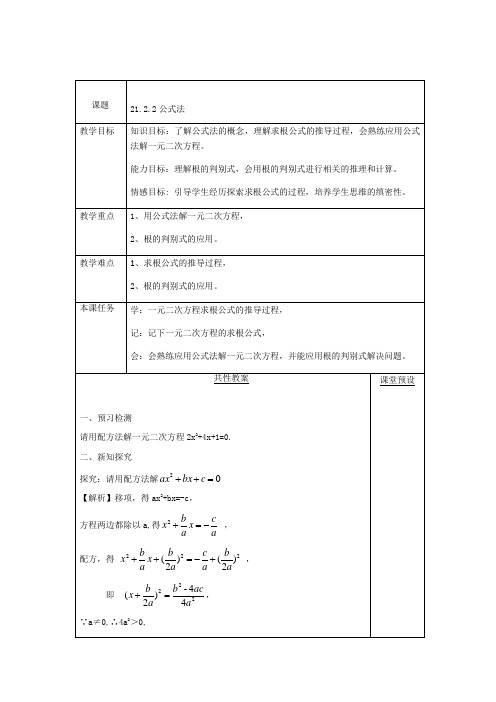


《公式法解一元二次方程》一、教学目标:知识目标:理解一元二次方程求根公式的推导过程,了解公式法的概念,会熟练运用公式法解一元二次方程。
能力目标:(1)通过求根公式的推导,加强推理技能的训练,培养学生数学推理的严密性及严谨性。
(2)培养学生准确快速的计算能力。
情感目标:(1)通过公式的引入,培养学生寻求简便方法的探索精神及创新意识。
(2)通过求根公式的推导,渗透分类讨论的数学思想。
二、教学重难点重点:求根公式的推导及公式法的应用难点:对求根公式推导过程中依据的理论的深刻理解。
三、教学过程温故知新1」用配方法解一元二次方程方程(1)x2-4x-3=0探索新知1、学生自主探究根据幻灯上展示的用配方法的步骤解一元二次方程2、合作交流:将自己的问题在小组内交流寻求帮助,并给出以下几个问题在小组内讨论交流问题:(1)哪些一元二次方程适合用直接开平方法解?(mx+n)2=p(p≥0)(2)在开方时,方程右边的数含有字母系数,你能确定它的正负吗?包含几种情况?在这呢我引导学生发现他有可能大于0、小于0、也有可能等于0(3)b 2 -4ac 的正负由谁来决定?为什么?这些问题解决了一元二次方程方程的根也就求出来了再返回去,引导学生发现b平方减4ac的正负与一元二次方程跟之间的关系:当它大于0时,方程有两个不相等的实数根,当它等于0时,方程有两个相等的实数根,当它小于0时,方程无实数根,(再幻灯上展示)既然知道了它们之间存在这样的关系,那么通过计算b平方减4ac的值,并与0作比较,就能判断出一元二次方程根的情况,所以我们把式子b平方减4ac来表示,引导学生通过上面的解答过程,发现当b平方减4ac大于或等于时,方程有实数根大于或等于0时,方程有实数根为:aacbbx242-±-=也就是说当(042≥-acb)可以利用这个公式可以求出方程的两根,把它就叫做一元二次方程的求根公式,用求根公式解方程的方法叫公式法。
教学目标1.会用根的判别式判断一个一元二次方程的根的情况。
2.会运用根的判别式求一元二次方程中字母系数的取值范围。
3.通过对问题的探究,进一步体会分类的数学思想,提高观察、分析、归纳的能力。
2学情分析本节课是在学生学习完一元二次方程后学习探索判断方程根的情况。
学生对一元二次方程的解法已经学习完直接开平方法、配方法和公式法,基本熟知解一元二次方程的基本思想——降次。
一元二次方程的根的判别式在整个中学数学中占有重要的地位,既可以根据它来判断一元二次方程的根的情况,又可以为今后研究不等式,二次三项式,二次函数,二次曲线等奠定基础,并且用它可以解决许多其它综合性问题。
通过这一节的学习,培养学生的探索精神和观察、分析、归纳的能力,以及逻辑思维能力、推理论证能力,并向学生渗透分类的数学思想,渗透数学的简洁美。
3重点难点重点:根的判别式的正确理解和运用难点:根的判别式的运用4教学过程4.1 第二学时4.1.1教学活动活动1【导入】一、知识回顾:用公式法解下列方程(1) 2x2-x-3=0 (2) 2x2-4x+2=0 (3) 4x2+x+1=0【用公式法解一元二次方程,从特殊的三个方程根的情况猜想任意一元二次方程根的情况,体现从特殊到一般的思想。
】一元二次方程ax2+bx+c=0(a≠0)的根的情况可由b2-4ac来判定。
我们把b2-4ac叫做一元二次方程的根的判别式,用“△”来表示。
(1)△>0时,方程有两个不相等的实数根;(2)△=0时,方程有两个相等的实数根;[△≥0时,方程有实数根](3)△<0时,方程没有实数根.活动2【讲授】二、新课讲授例1.不解方程,判断下列关于x的方程的根的情况(1) 2x2+3x-4=0(2) 4x2+9=12x(3) 5(x2+1)-7x=0(4) x2+(2k+1)x+k-1=0(5) x2+mx+2m-5=0【前三问直接用判别式进行判断即可,应用新知的能力。
第一讲 走进追问求根公式
形如02=++c bx ax (0≠a )的方程叫一元二次方程,配方法、公式法、因式分解法是解一元二次方程的基本方法.而公式法是解一元二次方程的最普遍、最具有一般性的方法. 求根公式a
ac b b x 2422,1-±-=内涵丰富:它包含了初中阶段已学过的全部代数运算;它回答了一元二次方程的诸如怎样求实根、实根的个数、何时有实根等基本问题;它展示了数学的简洁美.
降次转化是解方程的基本思想,有些条件中含有(或可转化为)一元二次方程相关的问题,直接求解可能给解题带来许多不便,往往不是去解这个二次方程,而是对方程进行适当的变形来代换,从而使问题易于解决.解题时常用到变形降次、整体代入、构造零值多项式等技巧与方法.
【例题求解】
【例1】满足1)1(22=--+n n n 的整数n 有 个.
思路点拨 从指数运算律、±1的特征人手,将问题转化为解方程.
【例2】设1x 、2x 是二次方程032=-+x x 的两个根,那么1942231+-x x 的值等于( )
A . 一4
B .8
C .6
D .0
思路点拨 求出1x 、2x 的值再代入计算,则计算繁难,解题的关键是利用根的定义及变形,使多项式降次,如1213x x -=,2223x x -=.
【例3】 解关于x 的方程02)1(2=+--a ax x a .
思路点拨 因不知晓原方程的类型,故需分01=-a 及01≠-a 两种情况讨论.
【例4】 设方程04122=---x x ,求满足该方程的所有根之和.
思路点拨 通过讨论,脱去绝对值符号,把绝对值方程转化为一般的一元二次方程求解.
【例5】 已知实数a 、b 、c 、d 互不相等,且x a
d d c c b b a =+=+=+=+1111, 试求x 的值.
思路点拨 运用连等式,通过迭代把b 、c 、d 用a 的代数式表示,由解方程求得x 的值.
注: 一元二次方程常见的变形形式有:
(1)把方程02=++c bx ax (0≠a )直接作零值多项式代换;
(2)把方程02=++c bx ax (0≠a )变形为c bx ax --=2,代换后降次;
(3)把方程02=++c bx ax (0≠a )变形为c bx ax -=+2或bx c ax -=+2,代换后使之转化关系或整体地消去x .
解合字母系数方程02=++c bx ax 时,在未指明方程类型时,应分0=a 及0≠a 两种情况讨论;解绝对值方程需脱去绝对值符号,并用到绝对值一些性质,如222
x x x ==.
学历训练
1.已知a 、b 是实数,且0262=-++b a ,那么关于x 的方程1)2(22-=++a x b x a 的根为 .
2.已知0232=--x x ,那么代数式11)1(23-+--x x x 的值是 .
3.若142=++y xy x ,282=++x xy y ,则y x +的值为 .
4.若两个方程02=++b ax x 和02=++a bx x 只有一个公共根,则( )
A .b a =
B .0=+b a
C .1=+b a
D .1-=+b a
5.当分式4
312++-x x 有意义时,x 的取值范围是( ) A .1-<x B .4>x C .41<<-x D .1-≠x 且4≠x
6.方程011)1(=+-++x x x x 的实根的个数是( )
A .0
B .1
C .2
D .3
7.解下列关于x 的方程:
(1)03)12()1(2=-+-+-m x m x m ; (2)012=--x x ; (3)x x x 26542-=-+.
8.已知0222=--x x ,求代数式)1)(3()3)(3()1(2--+-++-x x x x x 的值.
9.是否存在某个实数m ,使得方程022=++mx x 和022=++m x x 有且只有一个公共的实根?如果存在,求出这个实数m 及两方程的公共实根;如果不存在,请说明理由.
注: 解公共根问题的基本策略是:当方程的根有简单形式表示时,利用公共根相等求解,当方程的根不便于求出时,可设出公共根,设而不求,通过消去二次项寻找解题突破口.
10.若0152=+-x x ,则15
39222+++-x x x = .
11.已知m 、n 是有理数,方程02=++n mx x 有一个根是25-,则n m +的值为 .
12.已知a 是方程020002=--x x 的一个正根。
则代数式a
200012000120003+++的值为 . 13.对于方程m x x =+-222,如果方程实根的个数恰为3个,则m 值等于( )
A .1 n .2 C .3 D .2.5
14.自然数n 满足16162472)22()22(2-+--=--n n n n n n ,这样的n 的个数是( )
A .2
B .1
C .3
D .4
15.已知a 、b 都是负实数,且
0111=--+b a b a ,那么a b 的值是( ) A .215+ B .251- C .2
51+- D .251-- 16.已知3819-=x ,求15
82318262234+-++--x x x x x x 的值. 17.已知m 、n 是一元二次方程0720012=++x x 的两个根,求)82002)(62000
(22++++n m m m 的值.
18.在一个面积为l 的正方形中构造一个如下的小正方形:将正方形的
各边n 等分,然后将每个顶点和它相对顶点最近的分点连结起来,如图所示,若小正方形面积为3281
1,求n 的值. 19.已知方程0132=+-x x 的两根α、β也是方程024=+-q px x 的根,
求p 、q 的值.
20.如图,锐角△ABC 中,PQRS 是△ABC 的内接矩形,且S △ABC =n S 矩形PQRS ,其中n 为不小于3
的自然数.求证:
AB
BS 需为无理数.
参考答案。