认同一致性分析(计数型)
- 格式:ppt
- 大小:1.80 MB
- 文档页数:23


测量系统分析管理规定1.目的通过对关键测量设备进行MSA分析,确保关键测量设备能够提供高质量的测量数据,以及准确、精密地评定产品与过程的质量,为判断产品是否合格、过程是否稳定提供可靠保证。
2.适用范围公司各基地所有的关键测量设备。
3.定义3.1 关键测量设备:用来监视或者测量产品/过程的关键/重要特性的测量设备。
关键测量设备从以下测量设备中评选:3.1.1控制计划中列出的用来测量关键/重要特性的测量设备;3.1.2SPC时涉及到的测量设备;3.1.3客户指定要求做MSA的测量设备;3.1.4PPAP中要求做MSA的测量设备;4.职责4.1 计量中心4.1.1负责整体策划、制定MSA计划;4.1.2负责评定MSA方案;4.1.3负责监督数据收集过程;4.1.4负责分析数据并形成分析报告;4.1.5负责监督不合格机台改善过程;4.2 需求部门Demand departments4.2.1负责向计量中心提出MSA申请;.4.2.2负责选取分析样本;4.2.3负责收集分析数据;4.2.4负责实施不合格设备的改善;5.作业流程Operation process6.作业说明6.1 需求申请6.1.1分析时机1)首次使用前分析:关键测量设备在首次使用前,必须进行MSA;2)计划外分析:当关键测量设备涉及到以下情况,由计量中心判定是否需要进行计划外的分析;A 设备维修(例如对IV测试仪的滤光片、暗房、底座进行维护后,需进行MSA);B 升级后(包含软件升级和硬件升级);C 设备的使用地点有变动(搬动过程中对设备进行了拆卸及重新组装);D 设备的使用人员出现变动;E 新控制计划;F PPAP要求;3) 周期性分析:根据每一种关键测量设备的重要程度、数量以及分析方法,确定分析周期,定期给所有关键测量设备进行MSA分析。
6.1.2关键测量设备的状态符合“6.1.1分析时机”中的条款时,需求部门需向计量中心申请进行MSA,由计量中心判定是否需要进行分析。
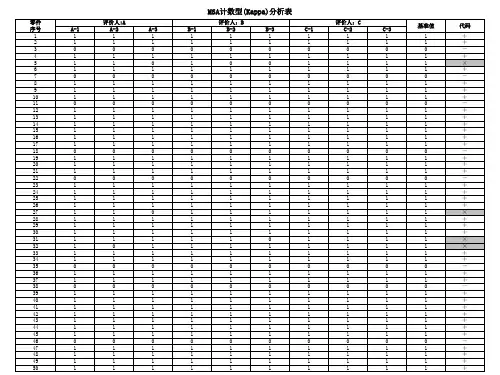
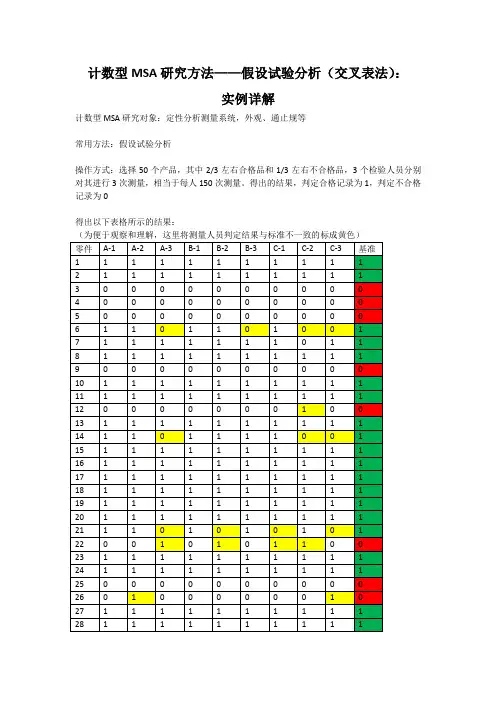
计数型MSA研究方法——假设试验分析(交叉表法):实例详解计数型MSA研究对象:定性分析测量系统,外观、通止规等常用方法:假设试验分析操作方式:选择50个产品,其中2/3左右合格品和1/3左右不合格品,3个检验人员分别对其进行3次测量,相当于每人150次测量。
得出的结果,判定合格记录为1,判定不合格记录为0得出以下表格所示的结果:(为便于观察和理解,这里将测量人员判定结果与标准不一致的标成黄色)计数型MSA的指标要求和计算:1、Kappa:判定人员一致性好坏的指标,接收准则:Kappa>0.75 1.1人员之间的一致性:期望发生的次数:根据判定结果的概率,会发生的次数A判定为0的概率=A判定为0的次数/A判定的总次数=(44+6)/150=0.333 A判定为1的概率=A判定为1的次数/A判定的总次数=(3+97)/150=0.667 B判定为0的概率=B判定为0的次数/A判定的总次数=(44+3)/150=0.313 B判定为1的概率=B判定为1的次数/A判定的总次数=(6+97)/150=0.687A判定为0,同时B判定为0的概率=0.333*0.313=0.104A判定为0,同时B判定为1的概率=0.333*0.687=0.229A判定为1,同时B判定为0的概率=0.667*0.313=0.209A判定为1,同时B判定为1的概率=0.667*0.687=0.458A判定为0,同时B判定为0期望的次数=0.104*150=15.6A判定为0,同时B判定为1期望的次数=0.229*150=34.35A判定为1,同时B判定为0期望的次数=0.209*150=31.35A判定为1,同时B判定为1期望的次数=0.458*150=68.7Po:A与B判定结果一致的概率=(44+97)/150=0.94Pe:期望结果一致的概率=(15.6+68.7)/150=0.562Kappa=== 0.863Kappa>0.75,说明A与B一致性较好A与C、B与C按相同方式计算并进行判定1.2人员与标准之间的一致性Po=(45+97)/150=0.947Pe=(16+68)/150=0.56Kappa=(0.947-0.56)/(1-0.56)=0.879Kappa>0.75,说明A与标准一致性较好B、C与标准的一致性按相同方式计算并进行判定2、有效率、漏判率、错判率:判定单个人员好坏的指标有效率:完全判定正确的零件个数/总零件个数漏判率:将不合格判定为合格的次数/标准为不合格的次数(Ⅱ类风险,顾客风险)错判率:将合格判定为不合格的次数/标准为合格的次数(Ⅰ类风险,工厂风险)根据数据计算结果:人员A有效率=42/50=84%人员A漏判率=3/48=6.25%人员A错判率=5/102=4.9%结果表明,人员A有效率位于可接受边缘,漏判率不接受,错判率接受。



计数型测量系统分析(MSA)计数型测量系统的最大特征是其测量值是一组有限的分类数,如合格、不合格、优、良、中、差、极差,等等。
当过程输出特性为计数型数据时,测量系统的分析方法会有所不同,一般可以从一致性比率和卡帕值两个方面着手考虑计数型测量系统分析。
➢计数型测量系统分析——一致性比率一致性比率是度量测量结果一致性最常用的一个统计量,计算公式可以统一地概括为:一致性比率=一致的次数/测量的总次数根据侧重点和比较对象的不同,又可以分为4大类。
1. 操作者对同一部件重复测量时应一致,这类似于计量型测量系统的重复性分析。
每个操作者内部的计数型测量系统都有各自的一致性比率。
2. 操作者不但对同一部件重复测量时应一致,而且应与该部件的标准值一致(若标准值已知),这类似于计量型系统的偏倚分析。
将每个操作者的计数型测量系统的结果与标准值相比较、分析,又有各自不同的一致性比率。
3. 所有操作者对同一部件重复测量时应一致,这类似计量型测量系统的再现性分析,操作者计数型测量系统分析之间有一个共同的一致性比率。
4. 各操作者不但对同一部件重复测量时应一致,而且应与该部件的标准值一致(若标准值已知)。
通常,使用这种一致性比率来衡量计数型测量系统的有效性。
一般说来,一致性比率至少要大于80%,最好达到90%以上。
当值小于80%,应采取纠正措施,以保证测量数据准确可靠。
➢计数型测量系统分析——卡帕值(k)K(希腊字母,读音kappa,中文为卡帕)是另一个度量测量结果一致程度的统计量,只用于两个变量具有相同的分级数和分级值的情况。
它的计算公式可以统一的概括为:以上公式中,P0为实际一致的比率;P e为期望一致的比率。
K在计算上有两种方法:Cohen 的k和Fleiss的k。
K的可能取值范围是从-1到1,当k为1时,表示两者完全一致;k为0时,表示一致程度不比偶然猜测好;当k为-1时,表示两者截然相反,判断完全不一致。
通常,k为负值的情况很少出现,下表归纳了常规情况下k的判断标准。
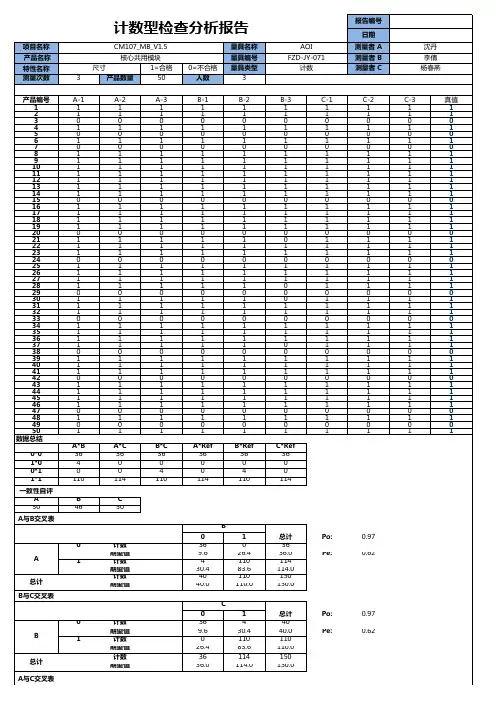


计数型GRR是什么
计数型GRR(Gauge Repeatability and Reproducibility for Attribute Data)是用于评估测量系统准确性的一种方法,特别是当测量数据是属性数据(非连续的,如合格/不合格)时。
与连续数据的GRR分析(通常用于测量物理量,如长度、重量等)不同,计数型GRR关注的是分类判断的一致性和准确性。
在计数型GRR中,重点在于评估以下两个方面:
1、重复性(Repeatability):这是指同一操作者使用相同的测量工具在重复条件下对同一样品进行多次测量时结果的一致性。
在计数型GRR中,这意味着检查一个操作者在重复判断同一样品时的一致性(例如,多次判断产品是否合格)。
2、再现性(Reproducibility):这是指不同操作者使用相同的测量工具和方法对同一样品进行测量时结果的一致性。
在计数型GRR中,这意味着检查不同操作者在对同一样品做出判断时的一致性(例如,不同人员判断同一产品的合格性)。
计数型GRR分析通常用于生产环境中,尤其是在质量控制过程中,当输出结果是基于分类判断(如合格/不合格,良品/次品)时。
它有助于识别和量化测量系统中的变异性,从而确保评估和控制过程的准确性和一致性。
通过计数型GRR分析,可以确定测量系统是否适合于其预定的用途,以及是否需要进一步的改进或校准。
1.目的保证公司有效展开测量系统分析(MSA工作,保证测量系统的可靠性,提高测量数据的质量,并为改进提供支持。
2.适用范围在控制计划中所要求的用于测量产品的特性与性能的测量系统。
3.引用文件《测量系统分析》第三版。
4.术语定义4.1.测量:赋值(或数)给具体事物以表示它们之间关于特定特性的关系。
4.2.量具:任何用来获得测量结果的装置,经常用来特指用在车间的装置,包括用来测量合格/不合格的装置.4.3.测量系统:用来对被测特性赋值的操作、程序、量具、设备、软件以及操作人员的集合,用来获得测量结果的整个过程.4.4.稳定性:是测量系统在某持续时间内测量同一基准或零件的单一特性时获得的测量值总变差. 偏倚:是测量结果的观测平均值与基准值的差值.4.5.线性:是在量具预期的工作范围内,偏倚值的差值.4.6.重复性(EV :是由一个检验员,采用一种测量仪器,多次测量同一零件的同一特性时获得的测量值变差.4.7.再现性(M):是由不同的检验员,采用相同的测量仪器,测量同一零件的同一特性时测量平均值的变差.4.8.零件变差(PV :不同零件之间的变差,零件在多人多次同一个量具测量出的平均值的变差。
4.9.总变差(TV :测量值与真值(基准值)之间的总变差。
4.10.检具能力:由检测设备的测量不确定度与检验特性的公差的比例关系确定.5.职责5.1.质量部负责并组织研发、生产等测量系统涉及人员实施测量系统分析5.2.新产品开发APQP组成员评价测量系统的可接收性,并对存在的问题采取纠正措施,根据测量, 在检验基准书上配置合适的量检具6.工作程序6.1.测量系统的分类6.1.1质量部组织确认测量系统类型,类型包括计量型测量系统、计数型测量系统、复杂测量系统、量化过度测量系统。
6.1.2质量部组织确认需要研究的范围计量型测量系统研究稳定性、偏倚、线性、重复性和再现性。
计数型测量系统研究检验员自身一致性、检验员之间一致性、检验员与标准之间一致性复杂测量系统研究稳定性和变异性6.2.计量型测量系统分析6.2.1仪器和人员的选择测量仪器必须是经过检定或校准合格,测量仪器分辨率的第一准则是能够分辨过程变差的10% 基于对整个测量系统的评价,从日常操作该仪器的人中挑选测量人。
计数型msa判定标准计数型MSA(Microbial Species Aggregates)是一种用于微生物分类的方法,可以判定和描述不同微生物的物种间关系和分类情况。
下面是一些与计数型MSA判定标准相关的参考内容,以帮助理解该方法:1. 基本原理:计数型MSA是通过分析不同微生物共同出现的频率和数量信息来判定它们的分类关系。
在一组样本中,如果两个微生物的共同出现频率和数量达到一定的阈值,就可以认为它们属于同一类或属于同一物种。
计数型MSA不依赖于微生物的遗传信息或形态特征,而是通过计数数据来进行分类。
2. MSA指标:计数型MSA使用一些指标来衡量微生物间的关系和分类情况。
常见的指标包括共现频率、共现数量、平均计数、标准差等。
这些指标可以通过在多个样本中计数微生物的出现情况来计算。
3. 阈值的确定:计数型MSA需要确定一些阈值来划分微生物的分类关系。
阈值可以基于实验数据进行确定,也可以通过统计分析来估计。
通常,阈值的选择要根据实验目的和研究者的经验来进行。
例如,可以根据共现频率和共现数量的分布情况,选择一个能够区分不同微生物群落的阈值。
4. 应用领域:计数型MSA广泛应用于微生物群落研究、环境监测、食品安全等领域。
通过该方法可以了解微生物之间的物种关系、生态角色和相互作用等信息,有助于深入理解微生物的生态系统。
5. 优缺点:计数型MSA的优点包括操作简单、成本低、适用范围广等。
同时,它也有一些局限性,比如对共生或互利共生关系的判断相对困难,对于稀有物种的判定可能存在误差等。
6. MSA在其他方法中的应用:计数型MSA和其他分类方法可以结合使用,相互补充。
例如,可以将计数型MSA的结果与基于遗传信息的分类方法进行对比,验证它们的一致性和可靠性。
7. 进一步研究:计数型MSA作为一种新兴的分类方法,仍有许多需要进一步研究的问题。
例如,如何更准确地选择阈值、如何解决不同样品中微生物计数数据的差异等。