阵列信号处理仿真作业
- 格式:doc
- 大小:621.00 KB
- 文档页数:5

1 阵列信号模型通常情况下,考虑M 元等距线阵,阵元间距为d ,且假设阵元均为各向同性阵元。
如图2.1所示,每个阵元后面接一路接收机,各阵元接收的信号进入自适应阵列处理器进行加权相加,得到阵列输出。
远场处有一个期望信号和P 个窄带干扰以平面波入射(波长为λ),期望信号到达角度为0θ,P 个干扰的角度分别为()1,2,,k k p θ= ,图2.1中Rc 代表各阵元接收机,()()()12,,,M x t x t x t 分别为M 个接收通道的输出信号,12,,,M w w w 分别为对各阵元通道接收信号的加权值。
()t w 阵列输出波前(等相位图2.1 自适应阵列空间位置关系示意图阵列接收的快拍数据可以表示为()()()t t t =+X AS n(2-1)式中,()t X 为1M ⨯阵列接收数据向量,()()()()12,,,TM t x t x t x t =⎡⎤⎣⎦X 。
[]T表示对矩阵进行转置,()t n 为1M ⨯的噪声向量,()()()()01,,,TP t s t s t s t =⎡⎤⎣⎦S 为信号复包络向量,()k s t 为第k 个信源复包络,()()()01,,,P θθθ=⎡⎤⎣⎦A a a a 为信号指向矩阵,其中,()()(1)1,,,,0,1,i iTj j N i i e e i P ββθ-⎡⎤===⎣⎦a a 为第i 个信号源的导向矢量,即2sin i i d πβθλ=(2-2)定义阵列的协方差矩阵为()()2H H x s n E t t σ⎡⎤==+⎣⎦R X X AR A I (2-3)式中,()()H s E t t ⎡⎤=⎣⎦R S S 为信号的协方差矩阵,I 为M 维单位矩阵,2n σ为阵元的噪声功率,本文中约定,[]T表示转置,[]*表示共轭,[]H表示共轭转置。
式(2-3)常由接收数据采样协方差矩阵ˆx R 代替,即()()11ˆNH xiii t t N==∑R x x(2-4)如图2.1所示的自适应阵列模型,阵列的M 个通道接收信号经加权处理后,最后的输出信号为()()()1MH i i i y t w x t t *===∑w x(2-5)阵列的方向图()p θ定义为()()H p θθ=w a(2-6)调整自适应阵列的权矢量w ,可以改变阵列的方向图,即改变各个方向上入射信号增益。

MUSIC 算法仿真实验一、数学模型与MUSIC 算法多重信号分类(MUSIC )算法的基本思想是将任意阵列输出数据的协方差矩阵进行特征分解,从而得到与信号分量相对应的信号子空间和与信号分量相正交的噪声子空间,然后利用这两个子空间的正交性来估计信号的参数。
考虑N 个远场信号入射到空间某阵列上,其中天线由M 个阵元组成。
当信号源是窄带的假设下,信号可用如下的复包络形式表示:00(()()()()()j t t i i j ii s t u t e s t s t e ωϕ)ωττ+−⎧=⎨−=⎩ (1) 第l 个阵元接收信号为1()()(),1,2,,Nl li i li l i x t g s t n t l τ==−+=∑"M (2)式中是第l 个阵元对第i 个信号的增益,表示第l 个阵元在t 时刻的噪声,li g ()l n t li τ表示第个信号到达第个阵元时相对于参考阵元的时延。
写为矩阵形式:i l()()()X t AS t N t =+ (3)[]12()()()()TM X t x t x t x t ="为1M ×维快拍数据矢量,[]12()()()()TM N t n t n t n t ="为1M ×维快拍噪声数据矢量,为12()[()()()]TN S t s t s t s t ="1N ×维空间信号矢量,为011012010210220201020111212122212NNM M MN 维流型矩阵(导向矢量阵),且 j j j N j j j N j j j M M MN g e g e g e g e g e g e A g e g e g e ωτωτωτωτωτωτωτωτωτ−−−−−−−−−⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦""##%#"M N ×10200[()()()]N A a a a ωω="ωN =" (4)假设阵列中各阵元是各向同性的且不存在通道不一致或互相耦合等因素的影响,则,此时导向矢量1,(,)({1,2,,},{1,2,,})ij g i j M N =∈""(5)010200()[],1,2,,ii Mi j j j T i a e e e i ωτωτωτω−−−="注意到通常τ与信号到达方向有关,因此问题可表述为:如何根据式(3)由接收到的数据()X t 去估计信号的参数,包括信号源数目,信号方向(与()S t N τ有关)等。
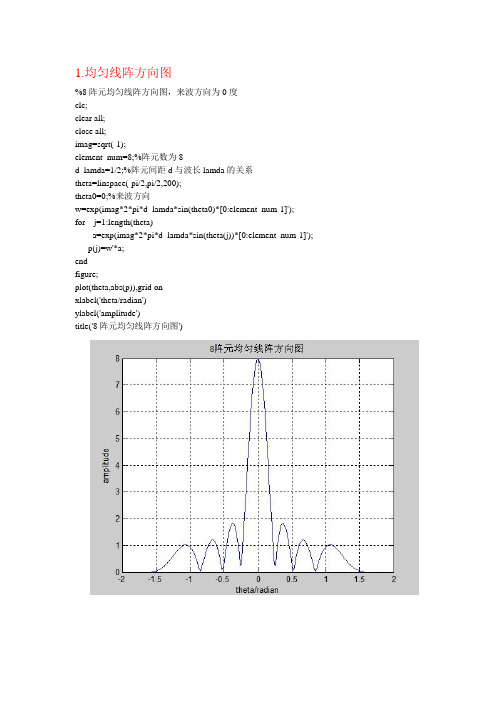
1.均匀线阵方向图%8阵元均匀线阵方向图,来波方向为0度clc;clear all;close all;imag=sqrt(-1);element_num=8;%阵元数为8d_lamda=1/2;%阵元间距d与波长lamda的关系theta=linspace(-pi/2,pi/2,200);theta0=0;%来波方向w=exp(imag*2*pi*d_lamda*sin(theta0)*[0:element_num-1]');for j=1:length(theta)a=exp(imag*2*pi*d_lamda*sin(theta(j))*[0:element_num-1]');p(j)=w'*a;endfigure;plot(theta,abs(p)),grid onxlabel('theta/radian')ylabel('amplitude')title('8阵元均匀线阵方向图')当来波方向为45度时,仿真图如下:8阵元均匀线阵方向图如下,来波方向为0度,20log(dB)随着阵元数的增加,波束宽度变窄,分辨力提高:仿真图如下:2.波束宽度与波达方向及阵元数的关系clcclear allclose allima=sqrt(-1);element_num1=16; %阵元数element_num2=128;element_num3=1024;lamda=0.03; %波长为0.03米d=1/2*lamda; %阵元间距与波长的关系theta=0:0.5:90;for j=1:length(theta);fai(j)=theta(j)*pi/180-asin(sin(theta(j)*pi/180)-lamda/(element_num1*d));psi(j)=theta(j)*pi/180-asin(sin(theta(j)*pi/180)-lamda/(element_num2*d));beta(j)=theta(j)*pi/180-asin(sin(theta(j)*pi/180)-lamda/(element_num3*d)); endfigure;plot(theta,fai,'r',theta,psi,'b',theta,beta,'g'),grid onxlabel('theta');ylabel('Width in radians')title('波束宽度与波达方向及阵元数的关系')仿真图如下:3. 当阵元间距时,会出现栅瓣,导致空间模糊。


现代信号处理仿作业(谐波恢复)现代信号处理仿作业(谐波恢复)————————————————————————————————作者:————————————————————————————————日期:现代信号处理仿真作业一(3.18谐波恢复)班级:自研42 姓名:李琳琳学号:2004211068一.谐波恢复的基本理论与方法:1. Pisarenko 谐波分解理论谐波过程可用差分方程描述,首先利用Pisarenko 谐波分解理论推导谐波过程所对应的差分方程。
对单个正弦波()sin(2)x n fn πθ=+利用三角函数恒等式,有:()2cos(2)(1)(2)0x n f x n x n π--+-=对上式作z 变换,得:12[12cos(2)]()0f z z X z π---+=得到特征多项式:1212cos(2)0f z z π---+=。
由此可见,正弦波的频率可以由相应特征方程的一对共轭根来决定:|arctan[Im()/Re()]|/2i i i f z z π=将单个正弦波推广到多个正弦波的情形,得:如果p 个实的正弦波信号没有重复频率的话,则这p 个频率应该由特征多项式1(21)212110p p p a z a z z -----++++=K (1)的根决定。
由此可得到p 个实正弦波所组成的谐波过程可以用以下的差分方程进行描述:21()()0pi i x n a x n i =+-=∑这是一个无激励的AR 过程。
2. 谐波恢复的ARMA 建模法在无激励的AR 模型差分方程21()()0pi i x n a x n i =+-=∑两边同乘()x n k -,并取数学期望,则有:21()()0,px i x i R k a R k i k =+-=?∑ (2)正弦波过程一般是在加性白噪声中被观测的,设加性白噪声为()w n ,即观测过程为: 1()()()sin(2)()pi i i i y n x n w n A f n w n πθ==+=++∑,其中()w n 为0均值的高斯白噪声。
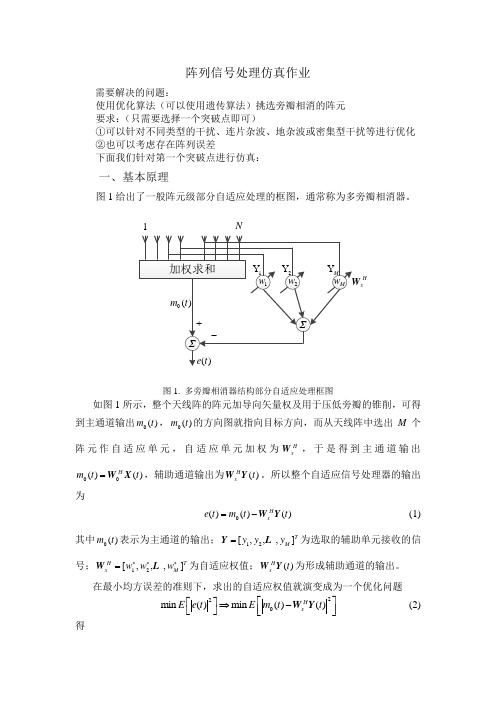
阵列信号处理仿真作业需要解决的问题:使用优化算法(可以使用遗传算法)挑选旁瓣相消的阵元 要求:(只需要选择一个突破点即可)①可以针对不同类型的干扰、连片杂波、地杂波或密集型干扰等进行优化 ②也可以考虑存在阵列误差下面我们针对第一个突破点进行仿真:一、基本原理图1给出了一般阵元级部分自适应处理的框图,通常称为多旁瓣相消器。
1NHx图1. 多旁瓣相消器结构部分自适应处理框图如图1所示,整个天线阵的阵元加导向矢量权及用于压低旁瓣的锥削,可得到主通道输出0()m t ,0()m t 的方向图就指向目标方向,而从天线阵中选出M 个阵元作自适应单元,自适应单元加权为H x W ,于是得到主通道输出00()()H m t t =W X ,辅助通道输出为()H x t W Y 。
所以整个自适应信号处理器的输出为0()()()H x e t m t t =-W Y(1)其中0()m t 表示为主通道的输出;12[,,,]T M y y y =Y L 为选取的辅助单元接收的信号;12[,,,]H Tx M w w w ***=W L 为自适应权值;()H x t W Y 为形成辅助通道的输出。
在最小均方误差的准则下,求出的自适应权值就演变成为一个优化问题220min ()min ()()H x E e t E m t t ⎡⎤⎡⎤⇒-⎢⎥⎣⎦⎣⎦W Y (2)得10()()()()H H xE t t E t m t -*⎡⎤⎡⎤=⎣⎦⎣⎦WY Y Y(3)为了保证目标信号不损失,应对自适应权作约束,约束条件是在目标信号的方向上,阵列自适应处理的增益为一常数。
即在权值调整过程中,无论权x W 怎样变化,对有用信号的增益不变。
这样在使自适应阵输出()e t 的均方值2()E e t ⎡⎤⎣⎦最小时,能最大限度地抑制干扰且不损失有用信号能量。
图1中应用式( 2) 的无约束优化方程显然不合理,它不能保证有用信号增益不变。
作业一 在球坐标系下推导平面波表达式球面波波动方程:22222222()E E x y z tεμ∂∂∂∂++=∂∂∂∂ 将直角坐标与球坐标的关系带入得到:22222222221111()(sin )sin sin s s sr r r r r r c tθθθθθϕ∂∂∂∂∂∂++=∂∂∂∂∂∂ 应用球面波方程一般都是球对称的,简化为:2222211()s sr r r r c t∂∂∂=∂∂∂ 经过变化,可得:222221rs rsr c t ∂∂=∂∂ 该方程的一个解为:exp[()As j t kr rω=- 同样有如下关系:/k c ω=根据平面波的定义,在球坐标系下,单频平面波的表达式为:(,)exp[()]As r t j t k r rω=-⋅作业二对于有限孔径的感应器,某一感应器接收的信号可以表示为:(,)()(,)z x t w x f x t =其中()w x 为窗函数。
通过空间傅立叶变换可得:()()exp()W k w x jk x dx ∞-∞=⋅⎰(,)(,)exp[()F k f x t j t k x dxdt ωω∞∞-∞-∞=--⋅⎰⎰对接收信号(,)z x t 进行傅立叶变换:()()()()[]()()()(){}()(),,exp[(),exp exp ,exp ,exp exp ,exp exp o Z k z x t j t k x dxdtw x f x t j t jk x dxdtw x F x jk x dxw x F l jl x dl jk x dx w x F l jl x jk ωωωωωω∞∞-∞-∞∞∞-∞-∞∞-∞∞∞-∞-∞∞∞-∞-∞=--⋅⎡⎤=-⋅⎣⎦⎡⎤=⋅⎣⎦⎡⎤⎡⎤=-⋅⋅⎣⎦⎣⎦⎡⎤=-⋅⋅⎣⎦⎰⎰⎰⎰⎰⎰⎰⎰⎰()()(){}()(),exp ,x dldxF l w x j k l x dx dlW k l F l dlωω∞∞-∞-∞∞-∞⎡⎤⎣⎦⎡⎤=-⋅⎣⎦=-⎰⎰⎰ 其中,()()[],,exp o F x f x t j t dt ωω∞-∞=-⎰。
阵列信号处理仿真作业
需要解决的问题:
使用优化算法(可以使用遗传算法)挑选旁瓣相消的阵元 要求:(只需要选择一个突破点即可)
①可以针对不同类型的干扰、连片杂波、地杂波或密集型干扰等进行优化 ②也可以考虑存在阵列误差
下面我们针对第一个突破点进行仿真:
一、基本原理
图1给出了一般阵元级部分自适应处理的框图,通常称为多旁瓣相消器。
1
N
H
x
图1. 多旁瓣相消器结构部分自适应处理框图
如图1所示,整个天线阵的阵元加导向矢量权及用于压低旁瓣的锥削,可得到主通道输出0()m t ,0()m t 的方向图就指向目标方向,而从天线阵中选出M 个阵元作自适应单元,自适应单元加权为H x W ,于是得到主通道输出
00()()H m t t =W X ,辅助通道输出为()H x t W Y 。
所以整个自适应信号处理器的输出为
0()()()H x e t m t t =-W Y
(1)
其中0()m t 表示为主通道的输出;12[,,,]T M y y y =Y L 为选取的辅助单元接收的信
号;12[,,,]H T
x M w w w ***=W L 为自适应权值;()H x t W Y 为形成辅助通道的输出。
在最小均方误差的准则下,求出的自适应权值就演变成为一个优化问题
220min ()min ()()H x E e t E m t t ⎡⎤⎡⎤⇒-⎢⎥⎣⎦⎣⎦
W Y (2)
得
1
0()()()()H H x
E t t E t m t -*
⎡⎤⎡⎤=⎣⎦⎣⎦W
Y Y Y
(3)
为了保证目标信号不损失,应对自适应权作约束,约束条件是在目标信号的
方向上,阵列自适应处理的增益为一常数。
即在权值调整过程中,无论权x W 怎
样变化,对有用信号的增益不变。
这样在使自适应阵输出()e t 的均方值2
()E e t ⎡⎤
⎣⎦
最小时,能最大限度地抑制干扰且不损失有用信号能量。
图1中应用式( 2) 的无
约束优化方程显然不合理,它不能保证有用信号增益不变。
即由于辅助通道中包含有用信号的能量,就会导致辅助阵元中目标信号分量与主通道中目标信号相减,引起目标信号对消,导致目标增益下降。
对此,应设法阻塞目标信号进入辅助支路,避免信号对消现象。
一种方法是在优化方程中加入单位增益约束,强制目标方向增益不变,这样的优化方程求解比较麻烦,而且不适合自适应单元自动选取的算法。
这里,采用信号阻塞矩阵来抑制目标信号,使目标信号能量不能进入辅助通道。
0=X JX
(4)
其中12[,,,]T N x x x =X L 为阵列信号;01020(1)0[,,,]T N x x x -=X L ;J 为信号阻塞矩阵(N -1)×N 。
在一般情况下,信号到达角为0θ,则信号阻塞矩阵J 可表示为
00001exp(())001exp(())01exp(())0
001exp(())j j j j ϕθϕθϕθϕθ⎡⎤--⎢⎥--=⎢⎥--⎢⎥--⎣⎦J L L L L 其中002()sin()d
πϕθθλ
=,当00θ=︒时,阻塞矩阵变为 11000110
0000
11-⎡⎤-⎢⎥⎢⎥=⎢
⎥⎢⎥⎢⎥-⎣⎦
J L
L L L
L L L
L 这样就得到整个自适应系统框图(图2)。
图2中上支路为主通道, 保证信号完全通过,其加权为导向矢量权和压低旁瓣的锥削。
下支路为辅助支路,信号阻塞矩阵阻止信号能量通过,将N 个阵元信号变成N -1个信号(降维),然后由辅助单元选择通路并选择参与自适应的单元,加自适应权后与上支路信号相减,得到自适应输出。
:N 阵元数
:J 信号阻塞矩阵:x W 自适应加权
:M 自适应单元数0:W 主通道加权
图2. 带信号阻塞矩阵的自适应系统框图
现在介绍一下辅助单元选取的准则。
由上面的分析可知,图2所示的辅助通道加了信号阻塞矩阵的自适应信号处理系统,将使目标信号增益不变。
由于干扰、信号、噪声相互独立,那么系统输出可分成信号能量、干扰能量和噪声能量。
在一定的信号环境中,系统对目标的增益不变决定了系统输出的信号能量不变,即不论自适应单元如何选取,也不论自适应权值如何变化,输出中包含的信号能量
始终不变。
这样,在信号环境不变的前提下,系统输出()e t 均方值越小2()E e t ⎡⎤⎣⎦
,
系统的信号与干扰噪声比就越大。
由上,可以在同一组快拍数据下,得到自适应
系统输出的()e t 的均方值2
()E e t ⎡⎤⎣⎦
,实际上就是系统输出能量作为选择自适应单
元好坏的标准。
二、利用遗传算法选取自适应单元
有了衡量自适应单元选取好坏的准则,下面就要解决如何用较小的运算量来
寻找较好的自适应单元的问题。
我们利用遗传算法寻优来解决自适应单元的选取。
假设阵元数为N ,欲寻找的辅助单元数为M 及辅助单元的组合顺序。
第一步:编码(产生初始种群)
由于自变量是要在总阵元中寻找到M 个(M <=N -1)辅助单元及其组合顺序。
信号经过阻塞矩阵后的输出N -1个信号,那么其可行解就有1M N C -种,
我们记自变量为121,,,,01,1,2,,1T
N i Q q q q q i N -⎡⎤===-⎣⎦L L 或(其中0i q =表示第i 个阵元没有被选中参与自适应过程,否则表示被选中参与自适应过程)。
我们对该可行解进行二进制编码,注意由于自变量Q 刚好是一个二进制序列,因此我们直接将该变量对应的序列当成编码。
我们随机的产生K 个(K <<1M
N C -)初始种群。
第二步:选取适应度函数
可以在同一组快拍数据下,得到自适应系统输出的()e t 的均方值2
()E e t ⎡⎤⎣⎦
,
实际上就是系统输出能量作为选择自适应单元好坏的标准。
由于均方值
2
()E e t ⎡⎤⎣⎦
越小,代表该自适应单元选取效果更好,因此我们选取适应度函数为
2
1
()()f Q E e t =
⎡⎤⎣⎦
(5)
由式(1)我们有
201
()()()H x f Q E m t t =
⎡⎤-⎢⎥⎣⎦
W Y (6)
为了能够在适应度函数()f Q 中体现自变量Q 和阻塞矩阵J ,我们需要将式(6)进行变形得到
22
001
1
()()()()()H H x x f Q E m t t E m t t =
=
⎡⎤⎡⎤--⎢⎥⎢⎥⎣⎦
⎣⎦
W Y W Y %% (7)
其中()t Q =∙Y JX %,其中的符号“∙”表示点乘操作。
x
W %表示与()t Y %同维数的权矢量,并且其中的一部分元素是将x W 中元素的与Q 中1的位置依次对应的,另一部分只要
是非零的数即可。
第三步:利用遗传算子,产生新一代的群体 (1)选择运算
遗传算法使用选择运算来实现对群体中的个体进行优胜劣汰操作:适应度高的个体被遗传到下一代群体中的概率大;适应度低的个体,被遗传到下一代群体中的概率小。
选择操作的任务就是按某种方法从父代群体中选取一些个体,遗传到下一代群体。
基本遗传算法(Simple Genetic Algorithms ,简称SGA ,又称简单遗传算法或标准遗传算法)中选择算子采用轮盘赌选择方法。
轮盘赌选择又称比例选择算子,它的基本思想是:各个个体被选中的概率与其适应度函数值大小成正比。
设群体大小为n ,个体i 的适应度为i F ,则个体i 被选中遗传到下一代群体的概率为:
1
i
i n
i
i F P F
==
∑
轮盘赌选择方法的实现步骤:
①计算群体中所有个体的适应度函数值(需要解码)
②利用比例选择算子的公式,计算每个个体被选中遗传到下一代群体的概率;
③采用模拟赌盘操作(即生成0到1之间的随机数与每个个体遗传到下一代
群体的概率进行匹配)来确定各个个体是否遗传到下一代群体中。
(2)交叉运算
所谓交叉运算,是指对两个相互配对的染色体依据交叉概率Pc 按某种方式相互交换其部分基因,从而形成两个新的个体。
交叉运算是遗传算法区别于其他进化算法的重要特征,它在遗传算法中起关键作用,是产生新个体的主要方法。
SGA中交叉算子采用单点交叉算子。
单点交叉算子的交叉位置是随机产生的。
(3)变异算子
所谓变异运算,是指依据变异概率Pm 将个体编码串中的某些基因值用其它基因值来替换,从而形成一个新的个体。
遗传算法中的变异运算是产生新个体的辅助方法,它决定了遗传算法的局部搜索能力,同时保持种群的多样性。
交叉运算和变异运算的相互配合,共同完成对搜索空间的全局搜索和局部搜索。
SGA 中变异算子采用基本位变异算子。
基本位变异算子是指对个体编码串随机指定的某一位或某几位基因作变异运算。
对于基本遗传算法中用二进制编码符号串所表示的个体,若需要进行变异操作的某一基因座上的原有基因值为0,则变异操作将其变为1;反之,若原有基因值为1,则变异操作将其变为0 。
经过上述三个运算步骤,将会产生相应的新一代群体。
然后判断新一代群体是否满足停止准则,若是满足,则输出结果并结束;若是不满足,则转到第三步,直到满足停止准则。