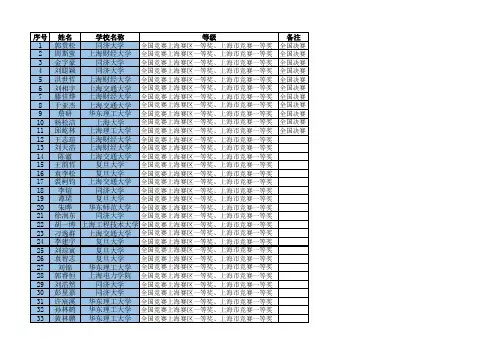
第十届全国大学生数学竞赛决赛(非数学类)获奖名单

山西大学学子获第十届全国大学生数学竞赛决赛一等奖等6 则作者：暂无来源：《山西教育·管理》 2019年第5期山西大学学子获第十届全国大学生数学竞赛决赛一等奖第十届全国大学生数学竞赛决赛于3 月29 日—31 日在哈尔滨工业大学举行，山西大学数学科学学院2016 级学生陈皓获数学专业高年级组一等奖，动力工程系2015 级学生王浩、2016 级学生刘森获得非数学专业三等奖。

第十届全国大学生数学竞赛参赛赛区达31 个，报名人数138832 人，包括北京大学、复旦大学、山东大学等参赛高校达784 所。

经过2018 年10 月的预赛，共有203 所高校的539名学生取得决赛资格。

本次决赛数学专业参赛人数191 人，其中高年级组获全国一等奖仅26 人。

本次竞赛实现了全国大学生数学竞赛山西省数学专业全国一等奖零的突破。

本次比赛所取得的成绩充分体现了山西大学以赛促教、以赛促学、以赛促创，积极推进学校学科竞赛的发展，充分发挥学科竞赛在创新型人才培养中的作用，不断提高人才培养的质量。

山西省教育厅组织收看全国综合防控儿童青少年近视暨推进学校卫生与健康教育工作视频会议4 月3 日下午，全国综合防控儿童青少年近视暨推进学校卫生与健康教育工作视频会议在京召开，我省设立分会场，组织省直有关部门，全国儿童青少年近视防控改革试验区、试点县（市、区）人民政府分管领导同志及相关部门负责同志，太原市部分中小学、幼儿园代表，以及省教育厅机关有关处室负责人收听收看。

省人民政府副省长张复明，省委教育工作委员会书记、省教育厅厅长吴俊清，省卫生健康委员会副主任武晋，省教育厅党组成员、副厅长任月忠参加了会议。

教育部党组书记、部长陈宝生指出，党中央、国务院高度重视儿童青少年身心健康。

儿童青少年近视问题是体现国家意志的政治问题、事关民族复兴和国家前途的重大问题、关系人民群众美好生活新期待的民心问题，我们要进一步深入贯彻落实习近平总书记关于防控近视工作的重要指示精神，提高政治站位，打好综合防控儿童青少年近视攻坚战，给党和人民群众交上一份合格的答卷。

十四届中国大学生数学竞赛获奖名单一、全国一等奖1.康宁，辽宁大学;2.陈思涛，北京大学;3.杨睿，清华大学;4.张浩然，复旦大学;5.林易，浙江大学;6.郑泽南，南京大学;7.郑浩，西安交通大学;8.郑文杰，武汉大学;9.蒋一帆，中南大学;10.熊昷，厦门大学;11.郑立灿，南开大学;12.贺雨桐，东南大学;13.马翔宇，太原理工大学;14.王云瀚，同济大学;15.李晗，电子科技大学;16.刘宇凡，中山大学;17. 郑小平，重庆邮电大学。

二、全国二等奖1.童维，西北工业大学;2.付新，西安电子科技大学;3.谭羽佳，南京航空航天大学;4.张涛，中国农业大学;5.杨汉龙，东北大学;6.谢嘉玮，上海交通大学;7.王峥然，中国科学技术大学;8.刘钰，哈尔滨工业大学;9.沈明雄，华东师范大学;10.孙名字，华中科技大学;11.许亮，南京农业大学;12.杨瑞昊，浙江师范大学;13.陶炜龙，合肥工业大学;14.张璇，北京师范大学;15.黄晓渝，中央民族大学;16.魏琪，苏州大学;17.周杨，北京交通大学;18.黄珩庆，中国人民大学;19.赵士卿，山东大学;20.李新，吉林大学。

三、全国三等奖1.马跃，北京航空航天大学;2.范苓，南京理工大学;3.张迪，湖南大学;4.罗家乐，深圳大学;5.李洋，大连理工大学;6.马艳秋，山东大学威海分校;7.丁耀，广西大学;8.王敏，安徽大学;9.马超，湖北大学;10.金鑫，西南大学;11.张俊宁，西安理工大学;12.马茹，西安科技大学;13.黄莎莎，中国矿业大学徐州校区;14.陈志伟，四川大学;15.孙健，武汉理工大学;16.赵洋，兰州大学;17.刘憬，深圳大学;18.李健，东北林业大学;19.崔传洁，河北工业大学;20.李益，北京科技大学。

四、特别奖1.郑凡，华南师范大学;2.刘磊，山西大学;3.张轩，西南民族大学;4.邓昊，四川师范大学;5.范妍，河南师范大学;6.李楠，江苏大学;7.丁晨，宁夏大学;8.陈江萁，云南大学;9.庞宗涛，福建师范大学;10.张志萍，山西农业大学;11.朱洋，西北农林科技大学;12.庞俊涛，浙江财经大学;13.张玉梅，青海大学;14.白赫，新疆师范大学;15.马昕，云南师范大学;16.刘浩，湖北中医药大学;17.曹舒，四川农业大学;18.李林，大连科技学院;19.张定祥，青岛大学;20.高雪琪，中国地质大学（武汉）。

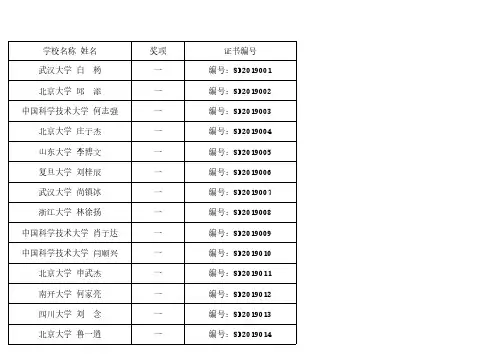
第十届全国大学生数学竞赛决赛试题参考答案及评分标准（非数学类，2019年3月30日）一、填空题（本题满分30分，每小题6分）1、设函数在点在处连续，则的值为答案：2、设则答案：3、设曲线L是空间区域的表面与平面的交线，则答案：4、设函数由方程确定，其中具有连续二阶偏导数，则答案：5、已知二次型，则的规范形为答案：二、设内三阶连续可导，满足，又设数列满足严格单调减少且计算【解】由于在区间（-1,1）内三阶可导，在处有Taylor公式又，所以分①由于数列严格单调且，则，且为严格单调增加趋于正无穷的数列，注意到，故由Stolz定理及①式，有分分三、设上具有连续导数，且证明：对于成立【证明】令则故函数在上严格单调增加，记的反函数为，则定义在上，且4分于是根据积分中值定理，存在使得分因此注意到则即分四、计算三重积分：，其中【解】采用“先二后一”法，并利用对称性，得其中分用极坐标计算二重积分，得交换积分次序，得分作变量代换:并利用对称性，得所以.分五、之和.【解】级数通项令分其中.因为所以满足解这个一阶线性方程，得由得,故且分六、设A是n阶幂零矩阵,即满足证明:若A的秩为r，且则存在n阶可逆矩阵P其中为r阶单位矩阵. 【证】存在n阶可逆矩阵H,Q，使得因为所以有分对QH作相应分块为则有因此分而所以显然，所以为行满秩矩阵.8分因为使得分令则有分七、设为单调递减的正实数列,收敛，证明：收敛，所以对任意给定，存在自然数，使得当时,有因为单调递减的正数列，所以分注意到当时，有令得到分下面证明：对于任意自然数n，如果满足则有事实上,即得到分利用（2），令可以得到即分又由知，存在自然数，使得分取则当时，有因此分。

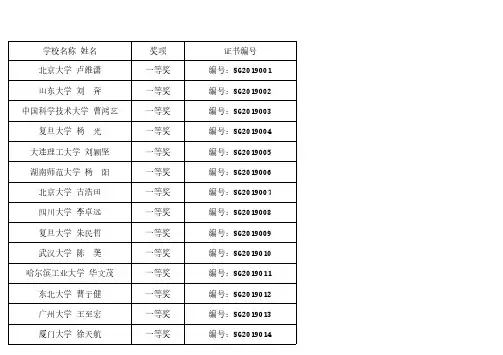
第十届全国大学生数学竞赛（非数学类）预赛试题及一、填空题（本题满分24分, 共4小题, 每小题6分)（1）设(0,1),α∈则()lim (1)n n n αα→+∞+-=＿＿＿＿＿＿＿.（2）若曲线()y y x =由+cos +sin 1yx t te ty t =⎧⎨+=⎩确定，则此曲线在0t =对应点处的切线方程为（3）23/2ln((1)x dx x ++⎰=（4）201-cos lim x x →=＿＿＿＿＿＿＿.f t ()0t ≠(1)0f =二 (本题满分8分) 设函数在时一阶连续可导，且，求函数f x -y 22()，使得曲线积分2222L ⎰y (2-f (x -y ))⎡⎤⎣⎦dx +xf (x -y )dy 与路径无关，其中L 为任一不与直=±y x 线相交的分段光滑闭曲线.f x ()0,11)3(f x ≤≤三 (本题满分14分) 设 在区间[ ]上连续，且 .证明：11141)3f (x )dx dx (f x ⎰≤≤⎰.四 (本题满分12分)计算三重积分22⎰⎰⎰x +y ()dV （V ）（V ），其中是由222x +y +(z -2)≥4，222x +y +(z -1)≤9，0z ≥所围成的空心立体.五 (本题满分14分) 设(,)f x y 在区域D M ≤，11(,)A x y ，22(,)B x y 是D 内两点，线段AB 包含在D 内。

证明：1122|(,)(,)|||f x y f x y M AB -≤，其AB ||AB 中表示线段的长度.)0(f x >六(本题满分14分) 证明：对于连续函数，有11lnf (x )dx ≥⎰⎰ln f (x )dx .七 (本题满分14分) 已知{}k a ，{}k b 是正项数列，且10,k k b b δ+-≥>，δ为一常数.证明：若级数1k k a +∞=∑收敛，则级数11k k k+∞=+.1,2,k。

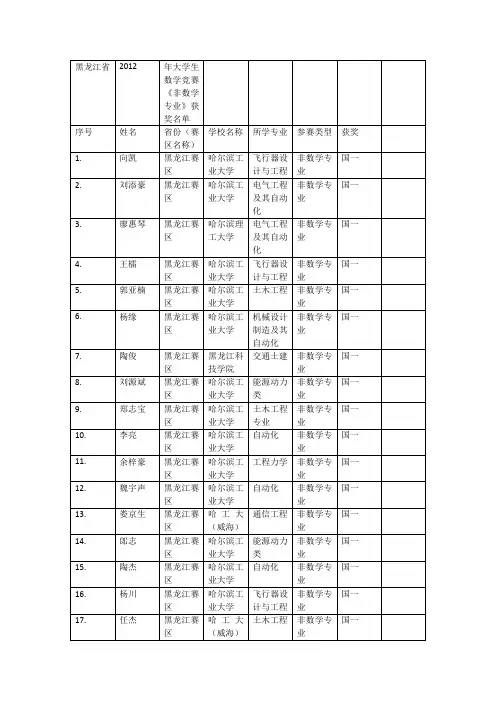
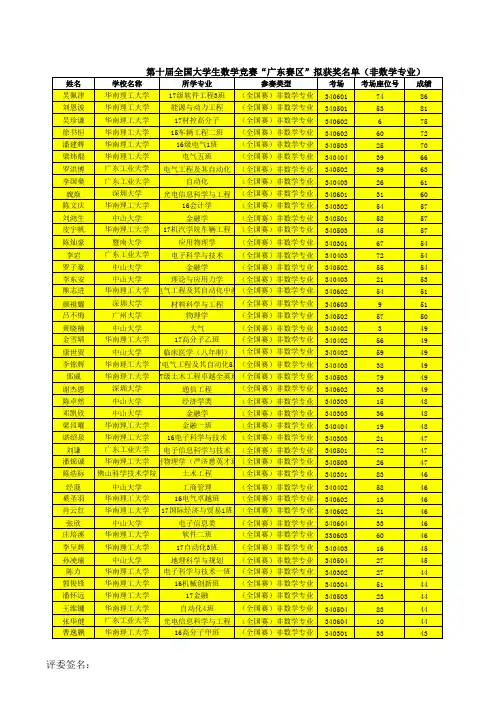
准考证号所在赛区姓名学校获奖等级201151303河北马非河北师范大学一等奖201152103辽宁章世骏大连交通大学一等奖201153106上海马宇飞同济大学一等奖201153108上海何金强上海大学一等奖201153305浙江薛思润浙江工业大学一等奖201155104四川刘丛志西南交通大学一等奖201153201江苏江汇河海大学一等奖201156702北京李卫华北京航空航天大学一等奖201151109北京黄舟北京航空航天大学一等奖201151201天津许彬慈天津大学一等奖201152305黑龙江郭腾虎哈尔滨工业大学一等奖201153208江苏罗川南京工业大学一等奖201153107上海高龙飞同济大学一等奖201151106北京周龙飞北京理工大学一等奖201152105辽宁邵华大连理工大学一等奖201154209湖北庞博清武汉大学一等奖201151103北京程正谦北京大学一等奖201151111北京滕锡超北京航空航天大学一等奖201152308黑龙江侯建哈尔滨工业大学一等奖201153109上海林胤嘉同济大学一等奖201156701北京唐明智北京航空航天大学一等奖201151108北京孙磊北京航空航天大学一等奖201151207天津吴雨杭天津大学一等奖201153308浙江康恒一浙江大学一等奖201154202湖北韦绘兵华中科技大学一等奖201154204湖北刘芳华中科技大学一等奖201154205湖北王利华中科技大学一等奖201155103四川肖俊超四川大学一等奖201156604国防科大刘俊海军航空工程学院一等奖201151104北京曲振北京交通大学二等奖201151202天津孟凡超天津大学二等奖201153102上海汪洋华东理工大学二等奖201154208湖北李本哲武汉大学二等奖201156104陕西郑无索空军工程大学理学院二等奖201153303浙江郭宇浙江大学二等奖201153304浙江吕武略浙江大学二等奖201154303湖南吉立勇湖南科技大学二等奖201151204天津贺凯天津大学二等奖201151206天津张鸿翔天津大学二等奖201154206湖北杨飞华中科技大学二等奖201156605国防科大陈一帆国防科技大学二等奖201151105北京吴岳北京邮电大学二等奖201154203湖北吴育家华中科技大学二等奖201156105陕西刘伟伟西北大学二等奖201156601国防科大孟兴解放军理工大学二等奖201156607国防科大刘伟国防科技大学二等奖201151203天津侯剑堃天津大学二等奖201154207湖北赵天楷华中科技大学二等奖201151304河北俞鹏先东北大学秦皇岛分校二等奖201152101辽宁杨帆大连理工大学城市学院二等奖201152302黑龙江王鹏飞哈尔滨理工大学二等奖201153202江苏刘华江南京理工大学二等奖201153206江苏李文青南京工业大学二等奖201151401山西毛人杰太原理工大学二等奖201152307黑龙江郑杰东北林业大学二等奖201153103上海易江同济大学二等奖201151205天津赵鹏伟天津工业大学二等奖201153404安徽曹丁红合肥工业大学二等奖201154505广西吴秀广西大学二等奖201151112北京王悠北京科技大学二等奖201153105上海郜煜华东理工大学二等奖201153203江苏罗斌河海大学二等奖201153207江苏杨威河海大学二等奖201154305湖南吴晓风中南大学二等奖201155107四川涂新电子科技大学二等奖201154304湖南续立志湖南工业大学二等奖201153205江苏吴在强河海大学二等奖201151110北京张凯北京航空航天大学二等奖201151301河北张涛东北大学秦皇岛分校二等奖201152303黑龙江丁有爽哈尔滨工业大学二等奖201154502广西王荣广西民族大学二等奖201154504广西丁畅广西大学二等奖201156103陕西邱于保西安邮电学院二等奖201151113北京黄厚军北方工业大学二等奖201151114北京刘自强北京邮电大学二等奖201153306浙江吴楠浙江大学二等奖201154501广西赖廷煜广西师范大学二等奖201151118北京杨泽南北京科技大学二等奖201153204江苏黄安东南京理工大学二等奖201153605江西熊高鹏江西理工大学二等奖201151102北京付建龙北京大学二等奖201153311浙江应佳男浙江大学二等奖201153705山东杨羽昊 山东大学二等奖201156205甘肃刘帅兰州大学二等奖201156603国防科大段化杰解放军理工大学二等奖201153401安徽王武翟中国科大少年班学院二等奖201153403安徽潘照第中国科大物理学院二等奖201153706山东孙臻中国石油大学（华东）二等奖201154103河南祝钰枢河南大学二等奖201154201湖北郭乾东武汉大学二等奖201156101陕西张帅第二炮兵工程学院二等奖201156606国防科大孙宝全海军工程大学二等奖201151115北京熊浩北京科技大学二等奖201152104辽宁王旦大连理工大学二等奖201155002重庆徐图重庆邮电大学二等奖201151117北京褚世敢北京大学三等奖201152205吉林林忠劲长春理工大学三等奖201155101重庆朱小东电子科技大学三等奖201153501福建陈国锋福州大学三等奖201153603江西陈旭浪南昌工程学院三等奖201154302湖南杨鹏中南大学三等奖201153309浙江包思遥浙江大学三等奖201153405安徽朱多宾安徽工业大学三等奖201153502福建林志杰厦门理工学院三等奖201156106陕西李俊洁陕西科技大学三等奖201156204甘肃赵琴兰州大学三等奖201153101上海李旸同济大学三等奖201153402安徽朱长皓安徽工业大学三等奖201153704山东曹安州中国海洋大学三等奖201155003重庆余肇飞重庆大学三等奖201155106四川刘尧电子科技大学三等奖201151302河北张来园河北工业大学三等奖201153504福建王坤发福州大学三等奖201154104河南韩颖薇河南科技大学三等奖201152202吉林张宝骥长春理工大学三等奖201153707山东宗杰 山东大学三等奖201154101河南乔佳楠中原工学院三等奖201155007重庆姜昆重庆大学三等奖201155105四川吴晨电子科技大学三等奖201156202甘肃赵文闻陇东学院三等奖201151107北京吴泰霖北京大学三等奖201152106辽宁王楠大连海洋大学三等奖201155001重庆邹建林重庆理工大学三等奖201153503福建寇智慧福州大学三等奖201156602国防科大向新朋国防科技大学三等奖201152301黑龙江许金鑫哈尔滨工业大学三等奖201152304黑龙江钟建文哈尔滨工业大学三等奖201153602江西方赞江西理工大学三等奖201154301湖南魏松柏湖南师范大学三等奖201153104上海成茂华东理工大学三等奖201153302浙江倪彬鑫浙江工业大学三等奖201153406安徽严成合肥工业大学三等奖201153709山东李兵山东理工大学三等奖201153708山东洪蒂 滨州学院三等奖201152306黑龙江白瑾珺哈尔滨工业大学三等奖201153604江西李国樑江西科技师范学院三等奖201154503广西夏孝军广西大学三等奖201156107陕西张洪伦西安邮电学院三等奖201156703北京徐冬北京航空航天大学三等奖201153701山东陈亮 山东大学三等奖201155005重庆王亚伟重庆大学三等奖201156109陕西于杰第二炮兵工程学院三等奖201156403宁夏章良微宁夏大学三等奖201151116北京夏青中国矿业大学（北京）三等奖201154105河南李欣欣河南大学三等奖201155006重庆孟志高重庆大学三等奖201156201甘肃顾尚廉兰州交通大学三等奖201151403山西李瑞中北大学三等奖201152203吉林赵江龙吉林建筑工程学院三等奖201154102河南张聪聪黄淮学院三等奖201152108辽宁刘星星大连海洋大学三等奖201153209江苏陈亚南京理工大学三等奖201156108陕西陆黄超西安建筑科技大学三等奖201151405山西毛雅俊山西师范大学三等奖201152107辽宁吴帮雄辽宁工程技术大学三等奖201154602海南方伟琼州学院三等奖201151305河北谭湘林东北大学秦皇岛分校三等奖201153702山东陈祥芹山东理工大学三等奖201151404山西刘伟太原科技大学三等奖201152102辽宁张波辽宁工业大学三等奖201152201吉林胡国栋长春工业大学三等奖201153703山东王圣英 山东大学三等奖201154604海南张文凯琼州学院三等奖201155004重庆姜泽浩重庆理工大学三等奖201156401宁夏文渊北方民族大学三等奖201154601海南霍猛海南大学三亚学院三等奖201156402宁夏陈慧北方民族大学三等奖201156203甘肃林磊兰州理工大学三等奖201152204吉林吴健华长春大学三等奖201156102陕西陈军西北大学三等奖201156404宁夏李嘉北方民族大学三等奖201151406山西赵磊太原理工大学三等奖201154603海南李枚芳海南大学三等奖201154605海南杨建涛海南师范大学三等奖。

第十届全国大学生数学竞赛（非数学类）预赛试题及答案一、填空题（本题满分24分, 共4小题, 每小题6分)（1）设(0,1),α∈则()lim (1)n n n αα→+∞+-=＿0＿＿＿＿＿＿.解 由于 1111,n n α⎛⎫⎛⎫+<+ ⎪ ⎪⎝⎭⎝⎭则 αααααα-=⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+<⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+=-+11111111)1(n n n n n n n ， 于是 ααα-<-+<11)1(0nn n ，应用两边夹法则，()lim (1)0n n n αα→+∞+-=. （2）若曲线()y y x =由+cos +sin 1yx t t e ty t =⎧⎨+=⎩确定，则此曲线在0t =对应点处的切线方程为0(1)y x -=--解：当0t =时，1,0x y ==，对cos x t t =+两边关于t 求导：1sin dx t dt =-，01t dxdt ==， 对+sin 1y e ty t +=两边关于t 求导：cos 0y dy dy e y t t dt dt +++=，01t dy dt ==-， 则01t dydx ==-.所以，切线方程为0(1)y x -=--.（3）21ln(1)C 2x x +-++ 解1：tan ln(tan sec )ln(tan sec )sin sec x t t t dt t t d t t=+==+⎰⎰ln(tan sec )sin sin ln(tan sec )sint ln(tan sec )t t d t t t t d t t =+=+-+⎰⎰21sin ln(tan sec )sint(sec tan sec )tan sec t t t t t t dt t t =+-++⎰sin sin ln(tan sec )cos tt t t dt t=+-⎰21sin ln(tan sec )ln |cos |C ln(1)C 2t t t t x x =+++-++.解2：ln(x d =+⎰1x dx ⎛⎫=-21xx dxx=-+⎰21ln(1)C2x x-++（4）21coslimx x→-=＿＿＿3＿＿＿＿.解答：2001coslimx xxx→→⎡-=⎢⎣⎦211lim2x x→=+2211lim2x x x→⎡⎤=++⎢⎥⎣⎦1lim2x→=++⎢⎥⎣⎦220011cos21cos313lim lim1322322x xx xx x→→--=++=++=.二 (本题满分8分) 设函数()f t在0t≠时一阶连续可导，且(1)0f=，求函数22()f x y-，使得曲线积分2222(2())()Ly f x y dx xf x y dy⎡⎤--+-⎣⎦⎰与路径无关，其中L为任一不与直线y x=±相交的分段光滑闭曲线.解：设22(,)(2())P x y y f x y=--，22(,)()Q x y xf x y=-，由题设可知，积分与路径无关，于是有(,)Q x y Px y∂∂=∂∂，由此可知222222()()()1x y f x y f x y'--+-=-----------5分记22t x y=-，则得微分方程()()1tf t f t'+=，即(())1tf t'=，())tf t t C=+又(1))0f=，可得1,C=-1())1f tt=-，从而22221()1f x yx y-=--.------------8分三 (本题满分14分) 设()f x在区间[0,1]上连续，且1()3f x≤≤.证明：1100141()()3f x dx dxf x≤≤⎰⎰.证明. 由柯西不等式111()()f x dx dx f x ⎰⎰≥201⎛⎫= ⎪ ⎪⎝⎭⎰. --------4分 又由于 ()()()1()30f x f x --≤，则()()()1()3/()0f x f x f x --≤，即 3()4()f x f x +≤， 103()4()f x dx f x ⎛⎫+≤ ⎪⎝⎭⎰. ----------10分 由于21111000313()()()4()f x dx dx f x dx f x f x ⎛⎫≤+ ⎪⎝⎭⎰⎰⎰⎰故 11141()()3f x dx dx f x ≤≤⎰⎰. -----------14分 四 (本题满分12分)计算三重积分22()V xy dV +⎰⎰⎰（），其中V （）是由222(2)4x y z ++-≥，222(1)9x y z ++-≤，0z ≥所围成的空心立体.解：（1）1sin cos ,sin sin ,1cos ():03,0,02x r y r z r V r ϕθϕθϕϕπθπ==-=⎧⎨≤≤≤≤≤≤⎩123222225()8()sin sin 315V x y dV d d r r dr ππθϕϕϕπ+==⋅⋅⎰⎰⎰⎰⎰⎰ ----------4分 （2）2sin cos ,sin sin ,2cos ():02,0,02x r y r z r V r ϕθϕθϕϕπθπ==-=⎧⎨≤≤≤≤≤≤⎩222222225()8()sin sin 215V x y dV d d r r dr ππθϕϕϕπ+==⋅⋅⎰⎰⎰⎰⎰⎰ ----------8分 （3）3cos ,sin ,10():02x r y r z V r θθθπ⎧==≤≤⎪⎨≤≤≤≤⎪⎩3022223510()22()1)(1243)55V r x y dV rdrd dz d dr πθθπ≤+===-⋅+⎰⎰⎰⎰⎰⎰12322222222()()()()256()()()()3V V V V x y dV x y dV x y dV x y dV π+=+-+-+=⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰------12分 五 (本题满分14分) 设(,)f x y 在区域DM ≤，11(,)A x y ，22(,)B x y 是D 内两点，线段AB 包含在D 内。

2010年全国大学生数学竞赛获奖名单（安徽赛区）2010年全国大学生数学竞赛获奖名单第二届全国大学生数学竞赛安徽赛区数学专业获奖名单大学组序号姓名学校名称参赛类别赛区奖项1苏长剑中国科大华罗庚班数学专业赛区一等奖2杜润东中国科大华罗庚班数学专业赛区一等奖3韩邦先中国科大数学系数学专业赛区一等奖4刘彦麟中国科大华罗庚班数学专业赛区一等奖5万喆彦中国科大数学系数学专业赛区一等奖6王华中国科大数学系数学专业赛区一等奖7胡越中国科大华罗庚班数学专业赛区一等奖8吴思鑫中国科大数学系数学专业赛区二等奖9权超禹中国科大华罗庚班数学专业赛区二等奖10高悦安徽大学数学专业赛区二等奖11冯骁毅中国科大华罗庚班数学专业赛区二等奖12徐海峰中国科大华罗庚班数学专业赛区二等奖13陈俊敏安徽师范大学数学专业赛区二等奖14晏明涵中国科大华罗庚班数学专业赛区三等奖15方龙飞安徽理工大学数学专业赛区三等奖16孙伟枫中国科大数学系数学专业赛区三等奖17陈同舟中国科大华罗庚班数学专业赛区三等奖18常天根中国科大数学系数学专业赛区三等奖19郑骞合肥工业大学数学专业赛区三等奖20彭丰斌安徽理工大学数学专业赛区三等奖21王鹏中国科大数学系数学专业赛区三等奖22雷闻宇中国科大数学系数学专业赛区三等奖23许广繁合肥工业大学数学专业赛区三等奖学院组序号姓名学校名称参赛类别赛区奖项1梁浩阜阳师范学院数学专业赛区一等奖2宋佳安庆师范学院数学专业赛区一等奖3汪飞巢湖学院数学专业赛区一等奖4汪华东黄山学院数学专业赛区一等奖5马超阜阳师范学院信息工程学院数学专业赛区二等奖6周国兵巢湖学院数学专业赛区二等奖7詹婷安庆师范学院数学专业赛区二等奖8张怀品滁州学院数学专业赛区二等奖9张蕊合肥师范学院数学专业赛区二等奖10蒋秀军安庆师范学院数学专业赛区二等奖11刘娟娟阜阳师范学院数学专业赛区三等奖12汪陈斯安庆师范学院数学专业赛区三等奖13操叶龙铜陵学院数学专业赛区三等奖14孙建举阜阳师范学院数学专业赛区三等奖15黄俊俊皖西学院数学专业赛区三等奖16卢霖宿州学院数学专业赛区三等奖17熊然合肥师范学院数学专业赛区三等奖18赵得扬阜阳师范学院信息工程学院数学专业赛区三等奖非数学专业获奖名单大学组序号姓名学校名称参赛类别赛区奖项1王武翟中国科大少年班学院非数学专业赛区一等奖2潘照第中国科大物理学院非数学专业赛区一等奖3朱多宾安徽工业大学非数学专业赛区一等奖4张棋中国科大信息学院非数学专业赛区一等奖5朱长皓安徽工业大学非数学专业赛区一等奖6曹丁红合肥工业大学非数学专业赛区一等奖7严成合肥工业大学非数学专业赛区一等奖8魏连风合肥工业大学非数学专业赛区二等奖9耿林合肥工业大学非数学专业赛区二等奖10林立枫中国科大少年班学院非数学专业赛区二等奖11刘迪源合肥工业大学非数学专业赛区二等奖12袁振亨安徽大学非数学专业赛区二等奖13曹朋朋合肥工业大学非数学专业赛区二等奖14时中中国科大物理学院非数学专业赛区二等奖15冯剑合肥工业大学非数学专业赛区二等奖16谢国涛合肥工业大学非数学专业赛区二等奖17朱程涛安徽大学非数学专业赛区三等奖18李柏中国科大少年班学院非数学专业赛区三等奖19吴德云安徽师范大学非数学专业赛区三等奖20佟亚楠合肥工业大学非数学专业赛区三等奖21朱峰安徽大学非数学专业赛区三等奖22胡友超安徽大学非数学专业赛区三等奖23涂江波安徽工业大学非数学专业赛区三等奖24陶诗飞安徽工业大学非数学专业赛区三等奖25葛凤琴安徽工业大学非数学专业赛区三等奖26苏来锁合肥工业大学非数学专业赛区三等奖27姚明波安徽大学非数学专业赛区三等奖28孟非凡安徽大学非数学专业赛区三等奖29张平安徽工程大学非数学专业赛区三等奖学院组序号姓名学校名称参赛类别赛区奖项1徐正正合肥学院非数学专业赛区一等奖2叶益龙黄山学院非数学专业赛区一等奖3陈荣梅合肥学院非数学专业赛区一等奖4徐凯黄山学院非数学专业赛区一等奖5方艳黄山学院非数学专业赛区一等奖6陈合理淮南师范学院非数学专业赛区一等奖7殷维维合肥学院非数学专业赛区一等奖8吴迎君淮南师范学院非数学专业赛区二等奖9胡佩佩铜陵学院非数学专业赛区二等奖10曹亚军合肥学院非数学专业赛区二等奖11胡雪峰合肥学院非数学专业赛区二等奖12叶超龙安庆师范学院非数学专业赛区二等奖13刘俊旭合肥学院非数学专业赛区二等奖14罗之虎阜阳师范学院非数学专业赛区二等奖15范娇铜陵学院非数学专业赛区二等奖16杨娟娟安庆师范学院非数学专业赛区二等奖17丁肇臻铜陵学院非数学专业赛区三等奖18余奎铜陵学院非数学专业赛区三等奖19魏胜黄山学院非数学专业赛区三等奖20王青合肥学院非数学专业赛区三等奖21秦帅铜陵学院非数学专业赛区三等奖22马慧敏黄山学院非数学专业赛区三等奖23徐冬生黄山学院非数学专业赛区三等奖24袁德飞皖西学院非数学专业赛区三等奖25程雷鸣淮南师范学院非数学专业赛区三等奖26潘义文合肥学院非数学专业赛区三等奖27李本亮合肥学院非数学专业赛区三等奖28王柳生合肥学院非数学专业赛区三等奖29干荣亮合肥师范学院非数学专业赛区三等奖30周登艳阜阳师范学院非数学专业赛区三等奖31陈士涛皖西学院非数学专业赛区三等奖32李鹏铜陵学院非数学专业赛区三等奖33金光勇黄山学院非数学专业赛区三等奖34曹祯记合肥学院非数学专业赛区三等奖35赵学茂合肥学院非数学专业赛区三等奖36杨德志阜阳师范学院非数学专业赛区三等奖37钱玉彬滁州学院非数学专业赛区三等奖38钱莉安庆师范学院非数学专业赛区三等奖39钟洋安庆师范学院非数学专业赛区三等奖40王龙安庆师范学院非数学专业赛区三等奖解放军电子工程学院获奖名单序号姓名学校名称参赛类别赛区奖项1陶会锋解放军电子工程学院非数学专业赛区一等奖2杨玚解放军电子工程学院非数学专业赛区二等奖3张渡兵解放军电子工程学院非数学专业赛区二等奖4吴重霄解放军电子工程学院非数学专业赛区三等奖5周龙健解放军电子工程学院非数学专业赛区三等奖6耿江解放军电子工程学院非数学专业赛区三等奖7朱中友解放军电子工程学院非数学专业赛区三等奖安徽省数学会2010．12．16。

全国大学生数学竞赛大纲（非数学专业类）为了进一步推动高等学校数学课程的改革和建设，提高大学数学课程的教学水平，激励大学生学习数学的兴趣，发现和选拔数学创新人才，更好地实现“中国大学生数学竞赛”的目标，特制订本大纲。

一、竞赛的性质和参赛对象“中国大学生数学竞赛”的目的是：激励大学生学习数学的兴趣，进一步推动高等学校数学课程的改革和建设，提高大学数学课程的教学水平，发现和选拔数学创新人才。

“中国大学生数学竞赛”的参赛对象为大学本科二年级及二年级以上的在校大学生。

二、竞赛的内容中国大学生数学竞赛（非数学专业类）竞赛内容为大学本科理工科专业高等数学课程的教学内容，具体内容如下：一、函数、极限、连续1．函数的概念及表示法、简单应用问题的函数关系的建立.2．函数的性质：有界性、单调性、周期性和奇偶性.3．复合函数、反函数、分段函数和隐函数、基本初等函数的性质及其图形、初等函数.4．数列极限与函数极限的定义及其性质、函数的左极限与右极限.5．无穷小和无穷大的概念及其关系、无穷小的性质及无穷小的比较.6．极限的四则运算、极限存在的单调有界准则和夹逼准则、两个重要极限.7．函数的连续性（含左连续与右连续）、函数间断点的类型.8．连续函数的性质和初等函数的连续性.9．闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理).二、一元函数微分学1. 导数和微分的概念、导数的几何意义和物理意义、函数的可导性与连续性之间的关系、平面曲线的切线和法线.2. 基本初等函数的导数、导数和微分的四则运算、一阶微分形式的不变性.3. 复合函数、反函数、隐函数以及参数方程所确定的函数的微分法.4. 高阶导数的概念、分段函数的二阶导数、某些简单函数的n阶导数.5. 微分中值定理，包括罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理.6. 洛必达(L’Hospital)法则与求未定式极限.7. 函数的极值、函数单调性、函数图形的凹凸性、拐点及渐近线(水平、铅直和斜渐近线)、函数图形的描绘.8. 函数最大值和最小值及其简单应用.9. 弧微分、曲率、曲率半径.三、一元函数积分学1. 原函数和不定积分的概念.2. 不定积分的基本性质、基本积分公式.3. 定积分的概念和基本性质、定积分中值定理、变上限定积分确定的函数及其导数、牛顿-莱布尼茨(Newton-Leibniz)公式.4. 不定积分和定积分的换元积分法与分部积分法.5. 有理函数、三角函数的有理式和简单无理函数的积分.6. 广义积分.7. 定积分的应用：平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力及函数的平均值．四.常微分方程1. 常微分方程的基本概念：微分方程及其解、阶、通解、初始条件和特解等.2. 变量可分离的微分方程、齐次微分方程、一阶线性微分方程、伯努利(Bernoulli)方程、全微分方程.3. 可用简单的变量代换求解的某些微分方程、可降阶的高阶微分方程：.4. 线性微分方程解的性质及解的结构定理.5. 二阶常系数齐次线性微分方程、高于二阶的某些常系数齐次线性微分方程.6. 简单的二阶常系数非齐次线性微分方程：自由项为多项式、指数函数、正弦函数、余弦函数，以及它们的和与积7. 欧拉(Euler)方程.8. 微分方程的简单应用五、向量代数和空间解析几何1. 向量的概念、向量的线性运算、向量的数量积和向量积、向量的混合积.2. 两向量垂直、平行的条件、两向量的夹角.3. 向量的坐标表达式及其运算、单位向量、方向数与方向余弦.4. 曲面方程和空间曲线方程的概念、平面方程、直线方程.5. 平面与平面、平面与直线、直线与直线的夹角以及平行、垂直的条件、点到平面和点到直线的距离.6. 球面、母线平行于坐标轴的柱面、旋转轴为坐标轴的旋转曲面的方程、常用的二次曲面方程及其图形.7. 空间曲线的参数方程和一般方程、空间曲线在坐标面上的投影曲线方程.六、多元函数微分学1. 多元函数的概念、二元函数的几何意义.2. 二元函数的极限和连续的概念、有界闭区域上多元连续函数的性质.3. 多元函数偏导数和全微分、全微分存在的必要条件和充分条件.4. 多元复合函数、隐函数的求导法.5. 二阶偏导数、方向导数和梯度.6. 空间曲线的切线和法平面、曲面的切平面和法线.7. 二元函数的二阶泰勒公式.8. 多元函数极值和条件极值、拉格朗日乘数法、多元函数的最大值、最小值及其简单应用.七、多元函数积分学1. 二重积分和三重积分的概念及性质、二重积分的计算(直角坐标、极坐标)、三重积分的计算(直角坐标、柱面坐标、球面坐标).2. 两类曲线积分的概念、性质及计算、两类曲线积分的关系.3. 格林(Green)公式、平面曲线积分与路径无关的条件、已知二元函数全微分求原函数.4. 两类曲面积分的概念、性质及计算、两类曲面积分的关系.5. 高斯(Gauss)公式、斯托克斯(Stokes)公式、散度和旋度的概念及计算.6. 重积分、曲线积分和曲面积分的应用(平面图形的面积、立体图形的体积、曲面面积、弧长、质量、质心、转动惯量、引力、功及流量等)八、无穷级数1. 常数项级数的收敛与发散、收敛级数的和、级数的基本性质与收敛的必要条件.2. 几何级数与p级数及其收敛性、正项级数收敛性的判别法、交错级数与莱布尼茨(Leibniz)判别法.3. 任意项级数的绝对收敛与条件收敛.4. 函数项级数的收敛域与和函数的概念.5. 幂级数及其收敛半径、收敛区间（指开区间）、收敛域与和函数.6. 幂级数在其收敛区间内的基本性质(和函数的连续性、逐项求导和逐项积分)、简单幂级数的和函数的求法.7. 初等函数的幂级数展开式.8. 函数的傅里叶(Fourier)系数与傅里叶级数、狄利克雷(Dirichlei)定理、函数在[-l，l]上的傅里叶级数、函数在[0,l]上的正弦级数和余弦级数。