平行四边形中的面积问题

《平行四边形的面积》习题精选1．下面图中每个方格代表1平方厘米，请按要求画出平行四边形．（1）分别画出底边5厘米、高3厘米，底边3厘米、高5厘米的平行四边形和长是5厘米、宽是3厘米的长方形．数一数它们的面积是多少？（2）以5厘米长的线段为同一底边，画出高为3厘米的不同形状的平行四边形，你能画出多少个？你发现了什么？（3）以7厘米长的线段为同一底边，分别画出高为2厘米、4厘米、6厘米……的平行四边形，它的面积是怎样变化的？2．计算下面每个平行四边形的面积．3．量一量下面平行四边形的底和高的长度，并计算出它的面积．底是（）厘米；高是（）厘米．4．底/厘米85 31.6 34.8 13.2高/厘米34 10.9 21.5 8.5面积/平方厘米5．一块平行四边形的钢板，底是3.8米，高是1.5米，求它的面积．这块钢板1平方米重39千克，这块钢板重多少千克？6．一块平行四边形菜地，底是18.4米，高是9.2米．在这块地种茄子，每棵苗占地0.18平方米，这块地可种茄子多少棵？（得数保留整数）7．一块六边形水泥砖（如图），由三个面积相同的平行四边形组成．要铺300平方米地面大约需要多少块这样的水泥砖？参考答案1．（1）15平方厘米 15平方厘米 15平方厘米（2）无数个它们面积都相等（3）14平方厘米 28平方厘米 42平方厘米2．540m2 85.12cm23．略4．2890 344.44 748.2 112.25．5.7平方米 222.3千克6．169.28 ≈940棵7．≈2858块《平行四边形的面积》习题精选一、填空．1．4.5平方米＝（）平方分米 2400平方厘米＝（）平方分米2．一个平行四边形的底是9分米，高是底的2倍，它的面积是（）平方分米．3．一个平行四边形的底是12厘米，面积是156平方厘米，高是（）厘米．4．一块平行四边形钢板，底是1.5米，高是1.2米，如果每平方米钢板重23.5千克，这块钢板重（）千克．二、判断题．1．平行四边形的面积等于长方形面积．（）2．一个平行四边形的底是5分米，高是20厘米，面积是100平方分米．（）3．一个平行四边形面积是42平方米，高是6米，底是7米．（）三、选择题．1．下面的长方形和平行四边形面积（）a．相等b．不相等2．用木条钉成的长方形拉成一个平行四边形，它的高和面积（）a．都比原来大b．都比原来小c．都与原来相等3．平行四边形的底扩大3倍，高缩小3倍，面积（）a．扩大3倍b．缩小3倍c．不变d．不好判断四、评议．下面是四个平行四边形，小红认为它们的面积都是6平方厘米，你认为对吗？（单位：厘米）23323232五、已知下图中正方形的周长为36厘米，求平行四边形的面积．参考答案一、填空1．450 24 2．162 3．13 4．42．3二、判断题．1．（×） 2．（×） 3．（√）三、选择题．1．a 2．b 3．c四、评议．2332（√）（×）3232（√）（×）五、已知下图中正方形的周长为36厘米，求平行四边形的面积．36÷4＝9（厘米） 9×9＝81（平方厘米）《平行四边形的面积》典型例题例．求下面平行四边形的面积．分析：图中给出的两个已知条件并不是一组相对应的底和高，要根据平行四边形“对边相等”的特性可以得出和高（6厘米）相对应的底也是4厘米，利用平行四边形的面积公式可以求出它的面积．解：2464=⨯（平方厘米）答：这个平行四边形的面积是24平方厘米．《平行四边形的面积》典型例题例．在两条平行线间画出两个平行四边形（如下图），试判断甲和乙谁的面积大？乙甲CB EFDA分析：平行四边形ABCD 和BCEF 是画在两条平行线之间，那么这两个平行四边形的高相等，因为两条平行线间的距离处处相等．这两个平行四边形都是以BC 为底，所以说这两个平行四边形的底也相等的．4厘米6厘米底和高都分别相等，那么底和高的乘积（面积）也相等，从两个面积相等的平行四边形中减去同样的一个三角形，剩下的面积也相等，所以甲和乙的面积是一样大的．解答：一样大．《平行四边形的面积》典型例题例．如图，正方形BDEC 周长是24厘米，平行四边形ADEB 面积是多少平方厘米？分析：从图上可以看出，平行四边形的底和高，都与正方形的边长相等．而正方形的边长是 （24÷4）厘米，所以平行四边形ADEB 的面积就是（24÷4）×（24÷4）＝6×6＝36（平方厘米）答：平行四边形ADEB 面积是36平方厘米．《平行四边形的面积》典型例题例．求下面平行四边形的周长（单位：分米）1267分析：已知平行四边形的一组底和高分别是12分米和7分米，可以求出它的面积是84712=⨯（平方分米），通过“平行四边形面积＝底×高”，可以逆推出：底＝平行四边形面积÷高，已知面积是84平方分米，高是6分米，可以求出和6分米相对应的底，用14684=÷（分米），平行四边形对边相等，已知平行四边形相邻的两条边分别是12分米和14分米，就可以求出它的周长．解：5221412=⨯+）（（分米）答：这个平行四边形的周长是52分米．《平行四边形的面积》典型例题例．一个平行四边形，若底增加2厘米，高不变，则面积增加6平方厘米；若高增加1厘米，底不变，则面积增加4平方厘米，原平行四边形的面积是多少？分析：要求原平行四边形的面积，必须知道原平行四边形的底和高．根据第一组条件，增加部分是一个底是2厘米，面积是6平方厘米的平行四边形，根据平行四边形的面积公式可以求出这个平行四边形的高，即求出原平行四边形的高．根据第二组条件，，增加部分是一个高为1厘米，面积为4平方厘米的平行四边形，由此可以求出增加部分的底，即求出原平行四边形的底．解：12)14()26(=÷⨯÷（平方厘米）答：原平行四边形的面积是12平方厘米．《平行四边形的面积》典型例题例．在一块长80米，宽35米的长方形地上，修了两条宽分别为3米和2米的通道，其余的地方铺上草皮（如图）．问：应铺多少平方米的草皮？分析：很显然，铺草皮的面积等于长方形的面积减去两条通道的面积，问题的关键是这两条 通道是什么图形？因为两条通道都是四边形，且两组对边分别平行，所以两条通道都是平行四边形．要求出这两个平行四边形的面积，底边分别是3米和2米，高是多少呢？这恐怕是个难点，你发现了吗？它们的高就是长方形的宽35米，问题得解．解：80×35－（3×35＋2×35） ＝2800－175＝2625（平方米）答：应铺2625平方米的草皮．《平行四边形的面积》典型例题例．如图，平行四边形的面积是150平方米，它的阴影部分的面积是多少平方米？分析：平行四边形的面积为已知，底边长已知，所以平行四边形的高可求出，由观察知阴影部分是一个直角梯形，这个直角梯形的上底为15米，下底为15－4＝11（米），高就是平行四边形的高，问题得解．解：[15＋（15－4）]×（150÷15）÷2＝26×10÷2＝130（平方米）答：阴影部分的面积是130平方米．。

第1篇一、引言平行四边形是一种常见的几何图形，它在数学、物理、工程等领域都有广泛的应用。

平行四边形的面积计算是基础数学知识的重要组成部分，也是培养学生逻辑思维能力和空间想象能力的重要途径。

本文旨在通过对平行四边形面积的推理，揭示其计算方法，为读者提供一种简洁、直观的解题思路。

二、平行四边形面积的定义平行四边形面积是指平行四边形内部所覆盖的区域大小。

设平行四边形ABCD的底边为AB，高为h，则平行四边形ABCD的面积S可以表示为：S = 底边AB × 高h三、平行四边形面积推理过程1. 拼接法将两个完全相同的平行四边形拼接在一起，形成一个长方形。

由于两个平行四边形完全相同，所以拼接后的长方形的长等于平行四边形的底边AB，宽等于平行四边形的高h。

因此，长方形的面积等于两个平行四边形面积之和：长方形面积= 2 × 平行四边形ABCD的面积即：AB × h = 2S解得：S = AB × h / 22. 切割法将平行四边形ABCD沿着高h切割成两个三角形ABC和ABD。

由于三角形ABC和ABD 的高都是h，底边都是AB，所以两个三角形的面积相等：三角形ABC的面积 = 三角形ABD的面积即：(AB × h) / 2 = (AB × h) / 2因此，平行四边形ABCD的面积S等于三角形ABC和ABD面积之和：S = 三角形ABC的面积 + 三角形ABD的面积即：S = (AB × h) / 2 + (AB × h) / 2解得：S = AB × h3. 移动法将平行四边形ABCD沿着高h向上平移，使其与一个矩形重合。

此时，矩形的长等于平行四边形的底边AB，宽等于平行四边形的高h。

因此，矩形的面积等于平行四边形ABCD的面积：矩形面积 = 平行四边形ABCD的面积即：AB × h = S四、结论通过拼接法、切割法和移动法三种推理过程，我们得出平行四边形面积的计算公式：S = 底边AB × 高h。

6.1平行四边形的面积1．王老伯家一块平行四边形菜地,底边长8米,高6米,已知平均每平方米可收青菜15千克,这块菜地可以收青菜多少千克？2．用一根铁丝折成一个长方形,这个长方形的长是12厘米、宽是8厘米．如果把它拉成一个平行四边形(如图),面积就减少了6平方厘米．平行四边形12厘米的底边上的高是多少厘米？3．用一根铁丝围成一个边长是8分米的正方形,如果把它拉成平行四边形,面积减少了16平方分米,这个平行四边形的高是多少分米？4．有一块平行四边形菜地,底40米,高25米,如果每平方米能收获7千克青菜．这块地一共可以收获多少千克青菜？5．一个平行四边形的果园内栽了1800棵果树,平均每棵果树占地10平方米,这个平行四边形果园的底是360米,高是多少米？6．一块平行四边形的土地,底是10.5米,高是6.4米．用这块地种辣椒,每棵辣椒占地0.2平方米,这块地一共可以种多少棵辣椒？7．植物是制造氧气的“工厂”,根据有关测算,1平方米的草坪,每天能够释放0.03千克的氧气．下图这块近似于平行四边形的草坪一周(按7天算)大约能释放氧气多少千克？8．一个平行四边形的菜地,高6米,底是高的3倍还多2米,这块地有多大？如果每平方米收菜5.5千克,一共收多少千克的菜？9．画出下面图形的高,并量出有用的数据标在图上,再计算图形的面积．10．一块平行四边形的麦地底是48米,高50米,如果每平方米收小麦4千克,这块地一共收小麦多少千克？11．如图是用1：400的比例尺画出的图形．先作出平行四边形的高,并量出有关的数据,(取整厘米数),再计算出这个平行四边形的实际面积是多少平方米？每平方米收小麦0.5千克,这块地可收小麦多少千克．12．干强胜老师准备在自家的空地开辟一块平行四边形的菜地,底是12米,比高长4米,这块菜地平均每平方米种3棵白菜,这块菜地一共可以种植多少棵白菜？13．在一块平行四边形地里共收稻谷32400千克．已知平行四边行地的底450米,高120米,平均每公顷产稻谷多少千克？14．一块平行四边形小麦地,底长80米,高是底的一半,平均每平方米可收小麦6.4千克．这块小麦地可收小麦多少千克？15．看图填表．(每个小方格的边长表示1cm．)平行四边形的面积a/cm h/cm S/cm2①②③16．一块平行四边形的麦地底是48米,高50米,如果每平方米收小麦4千克,这块地一共收小麦多少千克？17．有一条水渠穿过一块菜地(如图),这块菜地的面积是多少？18．如图中长方形的周长是20cm,计算平行四边形的面积．19．一块平行四边地,底长150m,高80m,这块地有多少公顷？在这块地里共收小麦7680千克,平均每公顷收小麦多少千克？20．计算如图所示每个平行四边形的面积,你发现了什么？21．如图,大平行四边形的面积是72cm2,图中小平行四边形(阴影部分)的面积是多少？22．如下图,一块近似平行四边形的草坪中间有条石子小路．如果铺好1平方米草坪需要12元,铺好这块草坪大约需要多少元？23．平行四边形的底扩大4倍,高扩大2倍,它的面积有什么变化？24．一块平行四边形的地,底边长1200米,高约为600米,在这块地里种小麦,平均每平方米可收小麦0.56千克,这块地共收割小麦多少千克？合多少吨？25．一块平行四边形的草地中有一条长8米、宽1米的小路,求草地的面积．参考答案1．8×6×15=48×15,=720(千克)．答：这块菜地可以收青菜720千克．2．(12×8﹣6)÷12,=(96﹣6)÷12,=90÷12,=7.5(厘米)．答：平行四边形12厘米的底边上的高是7.5厘米．3．(8×8﹣16)÷8,=(64﹣16)÷8,=48÷8,=6(分米)．答：这个平行四边形的高是6分米．4．7×(40×25),=7×1000,=7000(千克)；答：这块地一共可以收获7000千克青菜．5．1800×10÷360,=18000÷360,=50(米)．答：高是50米．6．5×6.4÷0.2,=67.2÷0.2,=336(棵),答：这块地一共可以种336棵辣椒．7．(20﹣1)×9×(0.03×7),=19×9×0.21,=171×0.21,=35.91(千克)；答：大约能释放氧气35.91千克．8．(6×3+2)×6,=20×6,=120(平方米),120×5.5=660(千克),答：这块地的面积是120平方米,可以收菜660千克．9．6×2.5,=15(平方分米)．答：平行四边形的面积是15平方分米．10．48×50×4,=2400×4,=9600(千克)．答：这块地一共收小麦9600千克．11．(1)实际的底为：3÷=1200(厘米),1200厘米=12米；实际的高为：2=800(厘米),800厘米=8米；平行四边形的实际面积是：12×8=96(平方米)；(2)0.5×96=48(千克),答：这个平行四边形的实际面积是96平方米；这块地可收小麦48千克．12．平行四边形的面积：12×(12﹣4),=12×8,=96(平方米)；一共种多少棵白菜：96×3=288(棵)．答：这块菜地一共可以种288棵白菜．13．450×120=54000(平方米)54000平方米=5.4公顷32400÷5.4=6000(千克)答：平均每公顷的稻谷产量是6000千克．14．80×(80÷2)×6.4=80×40×6.4,=3200×6.4,=20480(千克)；答：这块小麦地可收小麦20480千克．15．①3×3=9(平方厘米)；②2×4=8(平方厘米)；③4×3=12(平方厘米)．故答案为16．48×50×4,=2400×4,=9600(千克)．答：这块地一共收小麦9600千克．17．解：(40﹣5)×25,=35×25,=875(平方米)；答：这块菜地的面积是875平方米．18．解：(20÷2﹣4)×4,=6×4,=24(平方厘米),答：这个平行四边形的面积是24平方厘米．19．150×80=12000(平方米)12000平方米=1.2公顷7680÷1.2=6400(千克)答：这块地有1.2公顷,平均每公顷收小麦6400千克．20．(1)S=ah,=2×3,=6(平方分米)．(2)S=ah,=2×3,=6(平方分米)．(3)S=ah,=2×3,=6(平方分米)．我发现它们的面积都相等,它们的形状虽然不同,但是它们的高和底都相同．所以等底等高的平行四边形的面积相同．答：我发现等底等高的平行四边形的面积相同．21．解：72÷12×4,=6×4,=24(平方厘米),答：阴影部分的面积是24平方厘米．22．20×9-1×9=171(平方米)171×12=2052(元)23．解：因为平行四边形面积=底×高,底扩大4倍,高扩大2倍,则面积扩大了4×2=8倍,答：平行四边形的面积扩大8倍．24．56×(1200×600),=0.56×720000,=403200(千克),=403.2吨．答：这块地共收割小麦403200千克,合403.2吨．25．(20﹣1)×8=19×8,=152(平方米)；答：草地的面积为152平方米．。

（ 陶桥 ）小学（ 五 ）年级（一）班 胡屯镇联合校第三单元多边形面积的计算1·平行四边形面积的计算课题一：平行四边形面积的计算教学目的：1．使学生在理解的基础上掌握平行四边形的面积计算公式，能够正确地计算平行四边形的面积。

2．使学生通过操作和对图形的观察、比较，发展学生的空间观念，培养学生的分析、综合、抽象、概括和解决实际问题的能力。

教学重点：掌握平行四边形的面积计算公式，能够正确地计算平行四边形的面积。

教学难点：通过操作和对图形的观察、比较，发展学生的空间观念。

教具准备：参照教科书第70页的方格纸，投影片；教学过程：一、复习1．出示方格纸上画的平行四边形。

提问:方格纸上面的是什么图形？什么叫平行四边形？它有什么特征？2·让学生指出平行四边形的底，再指出它的高。

然后让每个学生在自己准备的平行四边形上画高。

（教师巡视，注意画得是否正确。

）教师：今天我们就来学习平行四边形面积的计算方法。

板书课题：平行四边形的面积二、新课1．用数方格的方法计算平行四边形的面积。

（1）我们在计算长方形的面积时，曾经用数方格的方法来计算它的面积，现在我们学习平行四边形面积的计算，也先用数方格的方法数一数它的面积是多少。

请打开教科书，看第70页上边的平行四边形图，每一个方格表示一平方厘米，自己数一数是多少平方厘米？请同学们认真观察一下，平行四边形在方格纸上出现了不满一格的，该怎么数呢？（可以都按半格计算。

）然后指名说出数得的结果，并说一说是怎样数的。

（2）出示方格纸上画的长方形，要求直接计算出它的面积。

然后指名说出计算结果。

（3）比较平行四边形和长方形。

提问：平行四边形的底和长方形的长有什么关系？平行四边形的高和长方形的宽呢？它们的面积怎么样？启发学生把比较的结果重复说一遍。

平行四边形的底和长方形的长，平行四边形的高和长方形的党分别相等，它们的面积也相等。

（4）小结：从上面的研究我们知道，平行四边形的面积也可以用数方格的方法求出来。

平行四边形的面积公式计算全文共四篇示例，供读者参考第一篇示例：平行四边形是几何学中非常重要的一个概念，它有着许多特殊的性质和公式。

其中面积公式计算是平行四边形的一个基础知识，能够帮助我们更好地理解和应用平行四边形的性质。

在本文中，我们将深入探讨平行四边形的面积公式计算方法，并结合实际例题进行详细说明。

让我们先来回顾一下平行四边形的定义。

平行四边形是一种具有两组平行的边的四边形，它有两对对边长度相等、对角线互相平分和夹角相等等特点。

根据平行四边形的性质，我们可以得知它的面积公式为：面积=底边长度*高。

接下来，让我们通过一个具体的例题来说明如何计算平行四边形的面积。

假设我们有一个平行四边形，其中底边长度为6cm，高为4cm。

我们需要计算这个平行四边形的面积。

根据上面提到的面积公式，我们可以直接将底边长度和高代入公式中进行计算。

所以这个平行四边形的面积为：6cm*4cm=24平方厘米。

如果我们知道平行四边形的对角线长度和夹角的话，也可以通过以下公式计算面积：面积=1/2*对角线1*对角线2*sin夹角。

这个公式是根据平行四边形的对角线长度和夹角的三角形特性推导得出的，可以帮助我们更快速地计算平行四边形的面积。

除了使用公式计算平行四边形的面积，我们还可以通过将平行四边形分解成矩形和三角形等简单图形来计算面积。

这种方法称为分割法，通过将平行四边形分割成简单的图形来计算每个小图形的面积，最后将所有小图形的面积相加得到平行四边形的面积。

这种方法在一些情况下比直接使用公式计算更加简便和直观。

计算平行四边形的面积需要我们熟练掌握面积公式和相关知识，通过实际例题的练习和思考来提高计算的准确性和效率。

希望通过本文的介绍和讲解，读者能够更加深入地理解和掌握平行四边形的面积计算方法，从而在数学学习和实际运用中更加得心应手。

【字数约800字】第二篇示例：平行四边形是几何学中的一种基本图形，其具有特定的性质和特点。

在学习平行四边形时，计算其面积是一个非常重要的内容。

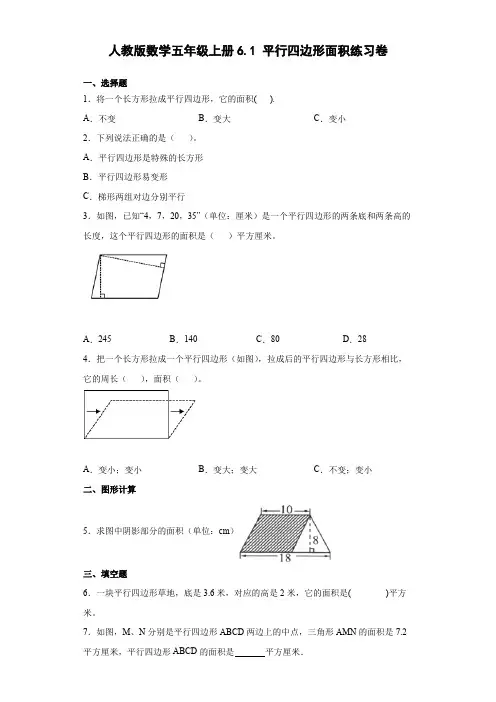
人教版数学五年级上册6.1 平行四边形面积练习卷一、选择题1．将一个长方形拉成平行四边形，它的面积().A．不变B．变大C．变小2．下列说法正确的是（）。

A．平行四边形是特殊的长方形B．平行四边形易变形C．梯形两组对边分别平行3．如图，已知“4，7，20，35”（单位：厘米）是一个平行四边形的两条底和两条高的长度，这个平行四边形的面积是（）平方厘米。

A．245B．140C．80D．284．把一个长方形拉成一个平行四边形（如图），拉成后的平行四边形与长方形相比，它的周长（），面积（）。

A．变小；变小B．变大；变大C．不变；变小二、图形计算5．求图中阴影部分的面积（单位：cm）三、填空题6．一块平行四边形草地，底是3.6米，对应的高是2米，它的面积是( )平方米。

7．如图，M、N分别是平行四边形ABCD两边上的中点，三角形AMN的面积是7.2平方厘米，平行四边形ABCD的面积是平方厘米．8．一个平行四边形相邻的两条边分别是4厘米和6厘米，如果较长边上的高是2厘米，那么这个平行四边形的面积是( )．9．如图，正方形ABCD的边长为4厘米，EF和BC平行，ECH的面积是7平方厘米，EG的长为( )。

10．把一个木条做成的长方形框架沿着对角拉成一个平行四边形，拉成后的平行四边形与原长方形比较，周长( )。

11．一个边长5厘米的正方形木框，拉成一个平行四边形后，面积减少了5平方厘米．拉成的平行四边形的高是厘米．四、判断题12．在平行四边形内画一个最大的三角形，三角形的面积一定等于平行四边形面积的一半。

( )13．两个平行四边形的面积相等，这两个平行四边形的形状也一定相同．_____．（判断对错）14．计算组合图形面积时，常用的方法有分割法和添补法．．15．一个平行四边形的高和底都扩大到原数的4倍，那么这个平行四边形的面积也要扩大到原数的4倍。

( )16．把平行四边形割补成一个长方形后,面积变小。

( )五、解答题17．植物园里有一个平行四边形的玫瑰园，玫瑰园的底是120m，高是60m，如果每平方米种8株玫瑰，这个玫瑰园一共能种多少株玫瑰？18．河西村有一块平行四边形的实验田，底长600米，高250米．平均每公顷收稻谷1.2吨，这块田可收稻谷多少吨？19．一个平行四边形，若底增加2厘米，高不变，则面积增加6平方厘米；若高增加1厘米，底不变，则面积增加4平方厘米，原平行四边形的面积是多少？参考答案：1．C【详解】2．B（1）平行四边形的两组对边平行且相等，长方形不仅两组对边平行且相等，四个角均为直角。

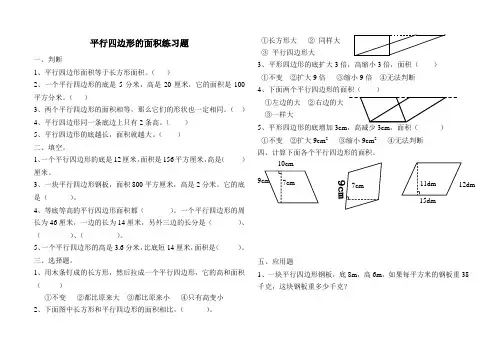
平行四边形的面积练习题一、判断1、平行四边形面积等于长方形面积。

（）2、一个平行四边形的底是5分米，高是20厘米，它的面积是100平方分米。

（）3、两个平行四边形的面积相等，那么它们的形状也一定相同。

（）4、平行四边形同一条底边上只有2条高。

（）5、平行四边形的底越长，面积就越大。

（）二、填空。

1、一个平行四边形的底是12厘米，面积是156平方厘米，高是（）厘米。

3、一块平行四边形钢板，面积800平方厘米，高是2分米。

它的底是（）。

4、等底等高的平行四边形面积都（）。

一个平行四边形的周长为46厘米，一边的长为14厘米，另外三边的长分是（）、（）、（）。

5、一个平行四边形的高是3.6分米，比底短14厘米，面积是（）。

三、选择题。

1、用木条钉成的长方形，然后拉成一个平行四边形，它的高和面积（）①不变②都比原来大③都比原来小④只有高变小2、下面图中长方形和平行四边形的面积相比，（）。

①长方形大②同样大③平行四边形大3、平形四边形的底扩大3倍，高缩小3倍，面积（）①不变②扩大9倍③缩小9倍④无法判断4、下面两个平行四边形的面积（）①左边的大②右边的大③一样大5、平形四边形的底增加3cm，高减少3cm，面积（）①不变②扩大9cm2③缩小9cm2④无法判断四、计算下面各个平行四边形的面积。

五、应用题1、一块平行四边形钢板，底8m，高6m，如果每平方米的钢板重38千克，这块钢板重多少千克？2、有两块面积相同的平行四边形地，一块地的的底是6米，高是3米，另一块地的底是9米，高是多少米？3、有一块平行四边形的草地，底是24米，高是底的一半，如果每平方米草地可以供3头羊吃一天，这块草地共可以供多少头羊吃一天？4、已知正方形周长为48cm，求下面平行四边形的面积。

5、如果用铁丝围成下图一样的平行四边形，需要多长的铁丝？6、一个平行四边形的周长是78cm（如图），以CD为底时，它的高是18cm，又BC是24cm，求它的面积。

6.1平行四边形的面积1．一个平行四边形果园,底长150米,高40米．如果这个果园一共种了1000棵果树,那么每棵果树平均占地多少平方米?2．一块平行四边形形稻田,底是90米,高60米,如果每平方米施肥0.2千克,这块稻田需施肥多少千克?3．一个平行四边形的面积是90平方厘米．它的底是15厘米,高是多少厘米?（列方程解）4．有一块平行四边形的菜地,底和高都是12米,它的面积是多少平方米?如果每平方米种10颗白菜,那么这块菜地一共可以种多少棵白菜?5．李大伯家有一块平行四边形的稻田,底是110m,是高的0.25倍．他今年计划每公顷稻田需施肥45kg,那么这块稻田共要施肥多少千克?6．有一块平行四边形的瓜地,底是6.8m,是高的2倍,如果每平方米栽瓜苗5棵,大约可栽多少棵瓜苗?7．如图,红星广告公司要将一块平行四边形的铁板的一面刷上油漆,如果每千克油漆能刷1.2平方米,这块铁板共需多少千克油漆?8．（如图）请回忆老师引导你推导平行四边形面积公式进的情境,给（1）、（2）填空；（3）计算．（1）以将平行四边形转化为长方形来推导平行四边形的面积公式．把平行四边形转化成长方形采用的方法是：（2）观察转化前的平行四边形与转化后的长方形,你发现了什么?（请写在下面的横线上,至少写三条）（3）计算上面平行四边形的面积.（先动手在图中量出计算时需要的数据,再算出它的面积）9．自己测量需要的数据,并求出图中草地的总面积．（测量数据以厘米为单位四舍五入到整数）10．张大爷有一块平行四边形的地,底长175米,高80米,今年共收绿豆2856千克,平均每公顷收绿豆多少千克?这块平行四边形的面积是多少平方米?合多少公顷呢?11．一块底长1.5米,高1.2米的平行四边形铁板．现在要油漆它的两面,每平方米用油漆0.3千克,一共要油漆多少千克?12．学校要制作一块平行四边形宣传牌,底长4米,高2米,如果广告公司制作广告牌每平方米收费30元,那么学校应支付给这个广告公司多少元?13．一块平行四边形的地,底边长250m,高84m,在这块地里种小麦,共收小麦14.7吨,平均每公顷收小麦多少吨?14．在一块底50m,高30m的平行四边形地里栽桃树,平均每6m2栽一棵,这块地能栽多少棵桃树?如果每棵收4.5kg桃子,这块土地共收桃子多少千克?15．有一块平行四边形的菜地,底长48米,高是底的一半,这块地的面积是多少平方米?16．画出下面图形的高,并量出有用的数据标在图上,再计算图形的面积．17．有一块平行四边形的麦田,底225米,高60米,共收小麦10.8吨,这块麦田有多少公顷?平均每公顷收小麦多少吨?18．一块平行四边形的花生地,底长45米,高18米,每平方米种花生6棵,每棵花生的产量约是0.8千克,这块花生地共收花生多少千克?19．一块平行四边形的地共收油菜籽3400kg,它的底长250m,高68m．平均每公顷收油菜籽多少千克?20．某乡镇中学开垦了一块平行四边形荒地种油菜,这块平行四边形地的底是32米,高是35米．如果平均每平方米收油菜1.5千克．这块地一共收油菜多少千克?21．如图,一块长方形草地,长方形的长是16米,宽是10米,中间铺了一条石子路。

一、填空：（每空 2 分，共 34 分）姓名：1、平行四边形的面积=（），公式用字母表示（）。

2、等底等高的平行四边形面积都（）。

3、平行四边形的高是 5 厘米，底是高的2 倍，它的面积是（）平方厘米。

4、把一个平行四边形沿此中一条高剪开，平移后能够拼成一个（），长方形的长就是平行四边形的（），长方形的宽就是平行四边形的（）。

5、 0.96公顷=（）平方米0. 65 平方千米 =（）公顷86000 平方米 =（）公顷8.96平方米=（）平方米（）平方分米7.28 平方米 =（）平方分米=（）平方厘米6、一个平行四边形的周长为52 厘米，一边的长为12 厘米，此外三边的长分是（）、（）、（）。

二、选择题。

（每空 2 分，共 10 分。

）1 、平行四边形的底扩大 6 倍，高不变，它的面积（）。

①不变②扩大 6倍③减小3倍④扩大2倍2 、用木条钉成的长方形拉成一个平行四边形，它的高和面积（）①不变②都比本来大③都比本来小④只有高变小3 、平行四边形同一底上能够画（）条高。

①无数②1③2④5①变大②不变③变小④没法比较三、画出以下各图形给定底边上的高。

（9 分）底底底四、解决问题。

（共 47 分）1、一个平行四边形的泊车场，底是65 米，高是24 米。

均匀每辆车占地15平方米，这个泊车场可泊车多少辆？（10 分）2、有一块平行四边形麦田，底是260 米，高是 75米，共收小麦15.6 吨。

这块麦田有多少公顷？均匀每公顷收小麦多少吨？（10 分）4 、将一个平行四边形剪开、平移拼成一个长方形，面积（），周长（）。

3 、如图，平行四边形的面积是64 平方米， A、 B 是上、下两边的中点，你能求出暗影部分的面积吗？（9分）AB4 、一个平行四边形的面积是42 平方米，高是7 米，它的底是多少米？（8分）5 、假如要用铁丝围成下边这样一个平行四边形，起码要用多少铁丝？（10分）6、一个平行四边形的周长是78cm（如图），以 CD为底时，它的高是18cm，又BC是 24cm，求它的面积。

教学内容：平行四边形面积的实际问题教学目的:1．使学生理解平行四边形面积计算公式的来源，能运用公式正确地计算平行四边形的面积，并会计算一些简单的有关平行四边形面积的实际问题。

2．培养学生初步的逻辑思维能力和空间观念。

3．结合教材渗透转化思想。

教学重点:掌握和运用平行四边形面积计算公式。

教学难点:平行四边形面积公式的推导过程。

课前准备:投影器、长方形框架、平行四边形纸片等。

教学过程:一、创设情境，引入新课师:自从我校开展科技小制作活动以来，同学们做了很多精美的小制作。

这是××同学制作的，大家认识它吗?生:长方形框架。

师:如果这个长方形长3分米，宽2分米，那么它的面积是多少?生:略师:老师如果捏住这个长方形的一组对角，向外拉，将拉成什么图形?生:平行四边形。

师:你们能猜出它的面积吗?生1:它的面积不变，还是6平方分米。

生2:它的面积比6平方分米小。

师:到底哪个答案正确?相信你们学了"平行四边形面积的计算"，就会茅塞顿开。

[评析:把长方形拉成平行四边形后，由于四条边的长度不变，所以不少学生认为其面积也不变。

这是学生认知中的误区，教者以此为契机，创设情境，导入新知，不但温习旧知，还设下悬念，激发学生的求知欲望。

]二、动手操作，推导公式师:(投影出示)这是画有两个不同图形的方格图（如下图所示），图中每个方格表示1平方厘米，不满一格的都按半格计算。

请大家看一看，想一想、议一议，可从中发现什么?生1:长方形的长与平行四边形的底相等。

生2:长方形的宽与平行四边形的高相等。

生3:长方形的面积与平行四边形的面积相等。

师:这几位同学回答得很好!综合他们的回答，我们可以得出一个什么样的结论?生:如果平行四边形的底和高分别与长方形的长和宽相等，那么它们的面积也相等。

[评析:让学生用数方格的方法初步感知平行四边形的面积及它与长方形面积相等的相关条件，符合小学生的思维特点，为新知学习扫除障碍，做好铺垫。

第2讲平行四边形的面积（讲义）小学数学五年级上册易错专项练（知识梳理+易错汇总+易错精讲+易错专练）1.图形面积的计算方法。

运用转化法求图形的面积。

把不规则的图形通过切割、平移等方法转化成学过的规则的基本图形，比如数方格法、割补法。

2.平行四边形面积计算公式的推导。

把平行四边形通过割补法变成长方形，通过长方形面积计算公式确定平行四边形面积计算公式。

3.平行四边形的面积计算公式。

平行四边形的面积＝底×高。

如果用S表示平行四边形的面积，用a表示平行四边形的底,用h表示平行四边形的高,那么平行四边形面积的计算公式可以写成S＝ah。

1. 每个平行四边形的底和高分别有两组，计算面积时要用相对应的一组底和高相乘。

2. 判断两个平行四边形的面积是否相等，应根据它们的底和高的具体情况进行判断。

3. 平行四边形的面积与它的底和高有关，底扩大到原来的n倍（n≠0），高缩小到原来的，面积不变。

【易错一】如图，平行四边形的高是8厘米，它的面积是（）平方厘米。

A．32 B．60 C．80 D．48【解题思路】依据在直角三角形中，斜边大于直角边可知：8厘米的高对应的底边是6厘米，于是可以利用平行四边形的面积＝底×高求解。

【完整解答】6×8＝48（平方厘米）；答：这个平行四边形的面积是48平方厘米。

故选D。

【易错点】此题主要考查平行四边形的面积的计算方法，关键是先确定出已知高所对应的底边。

【易错二】用木条钉成一个长方形框架，将这个长方形框架拉成一个平行四边形（如图）。

发现面积和周长有什么变化吗？发现：________________________________________【解题思路】用木条钉成一个长方形框架，然后把它拉成一个平行四边形，周长都是这四边，所以周长不变，拉成平行四边形之后高变短了，所以面积变小了，由此即可得出结论。

【完整解答】由分析可知：将一个长方形框架拉成一个平行四边形，会发现：周长不变，面积变小了。

平行四边形中的特殊面积关系1．问题引入平行四边形中涉及到很多面积计算问题，根据平行四边形的性质，可以得到一些特殊面积之间的规律性关系，掌握这些结论将有助于问题的求解。

下面是一个我们都很熟悉的结论：如图1，□ABCD 中对角线AC （或BD ）将平行四边形分成的两个三角形全等，因此有S △ABC =S △ADC =21S □ABCD （或S △ABD =S △CBD =21S □ABCD ）。

引例：如图，某村有一个呈四边形的池塘，在它的四个角的顶点A 、B 、C 、D 处均种有一棵大核桃树，该村准备开挖池塘建养鱼池，想使池塘面积扩大一倍，又不想移动核桃树，并要求扩建后的池塘成平行四边形形状，该村能否实现这一设想？若能，请你设计并画出图形；若不能，请你说明理由。

（画图要保留痕迹，不写画法）分析：连接对角线AC 、BD ，分别过点A ，B ，C ，D 作对角线的平行线，相交于点E 、F 、G 、H ，则□EFGH 即为所求。

2．问题拓展2.1．平行四边形对角线将平行四边形分成的四个三角形间的面积关系。

如图2，□ABCD 中对角线互相平分，OA=OC ，OB=OD ，易证△AOB ≌△COD ，△BOC≌△DOA ，所以S △AOB =S △COD ，S △BOC =S △DOA又由同底等高的三角形面积相等，可知：S △AOB = S △BOC故有：S △AOB =S △COD =S △BOC =S △DOA =41S □ABCD 拓展结论1：在平行四边形中，两条对角线将平行四边形分成的四个部分面积相等，且都等于平行四边形面积的四分之一。

例1．如图2，□ABCD 的对角线相交于O ，S △AOB =4cm 2，S □ABCD = 。

分析：由拓展结论1，S □ABCD =4 S △AOB =4×4=16（cm 2）2.2．平行四边形一条边上的点与其对边端点所连接的线段将平行四边形分成三个三角形间的面积关系。

平行四边形的面积计算与问题解析平行四边形是几何学中的一个常见形状，它具有特殊的性质和应用。

本文将介绍平行四边形的面积计算方法，并探讨一些与平行四边形面积相关的问题。

一、平行四边形的面积计算方法平行四边形的面积计算方法有几种，下面将介绍两种常用的方法。

方法一：基于底边和高的计算公式设平行四边形的底边长为a，高为h，则平行四边形的面积S可以通过以下公式计算：S = a * h方法二：基于两边长度和夹角的计算公式设平行四边形的两个相邻边长分别为a和b，它们之间的夹角为θ，则平行四边形的面积S可以通过以下公式计算：S = a * b * sin(θ)需要注意的是，使用这个公式时，夹角θ的取值应为其对应锐角的度数。

二、平行四边形面积的问题解析1. 如何确定平行四边形的底边和高？平行四边形的底边可以通过两个任意相邻边之一确定，高则是垂直于底边的线段。

根据给定的信息，我们可以通过测量或已知条件进行判断。

2. 如何确定平行四边形的两个相邻边和夹角？平行四边形的两个相邻边可以通过测量或已知条件确定。

夹角可以通过测量两边之间的角度得出。

3. 平行四边形与其他几何形状的关系平行四边形是梯形和矩形的特殊情况。

当一个四边形的对边平行且相等时，它就是一个平行四边形。

当四边形的所有角均为直角时，它就是一个矩形。

4. 如何计算由多个平行四边形组成的复杂图形的面积？当复杂图形由多个平行四边形组成时，可以通过将其分解为若干个平行四边形，计算每个平行四边形的面积，再将它们相加得到整个图形的面积。

5. 平行四边形面积计算的应用举例平行四边形的面积计算在实际中有广泛的应用。

例如，在建筑和土木工程中，可以通过计算平行四边形面积来确定场地的面积或物体的表面积。

在日常生活中，可以利用平行四边形面积计算来规划家具摆放或装修空间。

总结：本文介绍了平行四边形的面积计算方法，包括基于底边和高以及基于两边长度和夹角的计算公式。

同时，讨论了一些与平行四边形面积相关的问题，包括如何确定底边、高、相邻边和夹角，平行四边形与其他几何形状的关系，以及复杂图形的面积计算等。

【同步专练A 】6.1 平行四边形的面积（基础应用篇）一、单选题（共10题）1.两个完全一样的梯形可以拼成一个平行四边形,这个平行四边形的底等于( ).A . 梯形的上底B . 梯形的下底C . 梯形的高D . 梯形的上、下底之和2.一个平行四边形与一个三角形等底且面积相等,如果三角形的高是9厘米,那么平行四边形的高是（）厘米.A . 4.5B . 9C . 18D .223.平行四边形的底不变,高扩大2倍,它的面积（）.A . 扩大2倍B . 缩小2倍C . 无法确定D .扩大10倍4.一个三角形和一个平行四边形的底和面积都相等,那么三角形的高（）A . 和平行四边形的高相等B . 是平行四边形高的一半C . 是平行四边形高的2倍D . 是平行四边形高的4倍5.三角形和平行四边形的底相等,面积也相等.已知平行四边形的高是4厘米,三角形的高是（）厘米.A . 16B . 8C . 4D .156.如果三角形与平行四边形的面积与底都相等,已知平行四边形的高是8厘米,那么三角形的高应该是（）厘米.A . 4B . 8C . 16D . 无法确定7.一个平行四边形的底不变,高扩大到原来的4倍,它的面积( ).A . 扩大到原来的4倍B . 扩大到原来的2倍C . 不变D . 缩小到原来的8.有两个完全一样的梯形,它们的面积都是28平方厘米,把它们拼成一个平行四边形后,平行四边形的底是14厘米,高是（）厘米.A . 3B . 4C . 8D .119.如图,平行四边形的面积是（）平方厘米.A . 32B . 24C . 48D . 以上答案都不对10.一个平行四边形木框,拉成长方形后,面积（）.A . 变小B . 变大C . 不变D . 无法确定二、填空题（共10题）11.一个三角形的面积是25C m2 , 和它等底等高的平行四边形的面积是________．12.一个平行四边形的面积是156平方米,底是12米,高是________.13.一个三角形的底边长25厘米,高15厘米,这个三角形的面积是________平方厘米,和它等底等高的平行四边形的面积是________平方厘米.14.一个三角形的底是2.5m,高是2.8m,它的面积是________ m2 , 和它等底等高的平行四边形的面积是________ m2.15.一个三角形与一个平行四边形等底等高,如果三角形的面积是3.6平方分米,那么平行四边形的面积是________平方分米.16.一个平行四边形的面积是56平方分米,高4分米,底是________分米.17.一个正方形的周长是32C m,那么它的边长是________C m,面积是________ C m² .18.把一个长方形框架拉成平行四边形,这个平行四边形与原来的长方形相比,它的周长________,面积________.A 、比原来大B 、比原来小C 、与原来一样大D .无法比较19.一个三角形与一个平行四边形面积相等,底也相等.如果三角形的高是14厘米,那么平行四边形的高是________厘米.20.一个平行四边形的面积是30C m2 , 与它等底等高的三角形的面积是________．三、判断题（共10题）21.三角形的面积总是平行四边形面积的一半.（）22.平行四边形的面积大于梯形面积. （）23.两个完全一样的梯形能拼成一个长方形．（）24.平行四边形的两组对边不但平行,而且相等. （）25.平行四边形的面积等于三角形面积的2倍．（）26.面积相等的两个平行四边形,它们的底和高不一定相等. （）27.把一个长方形木框拉成平行四边形,它的周长和面积都不变．28.周长相等的长方形和平行四边形,面积不一定相等.（）29.把一个木条钉成的长方形拉成一个平行四边形,它的面积不变．30.一个平行四边形的底扩大4倍,面积就扩大4倍.（）四、计算题（共2题）31.计算下面图形的面积.（1）（2）（3）32.计算如图各图形的面积．五、解决问题（共6题）33.一块占地3.9公顷的平行四边形地,高80米,底是多少米？34. 一块近似平行四边形的苗圃,在苗圃中有一条小路（如图）,请你求出苗圃的实际面积是多少平方米？35.有一块平行四边形的荔枝地,它的底是50米,高是24米.36.李大叔要在一块底是93m,高是15m的平行四边形的土地上栽果树,如果每棵果树占地4.5m2 , 这块土地一共能栽多少棵果树？37.一个平行四边形的钢板,底是2.4 m,高是0.5 m.如果每平方米钢板重39 kg,这块钢板大约重多少千克?(得数保留整数)38.用木条做成一个长方形框,如果把它拉成一个平行四边形,发生了怎样的变化？请判断并说明理由.参考答案一、单选题1. D2. A3. A4. C5. B6. C7. A8. B9. B10. B二、填空题11. 50平方厘米12. 13米13. 187.5；37514. 3.5；715. 7.216. 1417. 8；6418. C ；B19. 720. 15平方厘米三、判断题21. ×22. ×23. ×24. √25. ×26. √27. ×28. √29. ×30. ×四、计算题31.（1）解：19×13=247平方米（2）解：26×14=364平方分米（3）解：27.5×13=357.5平方厘米32.解：①3.5×2÷2=3.5（平方厘米）答：三角形的面积是3.5平方厘米．②3×2=6（平方厘米）答：平行四边形的面积是6平方厘米．③（2.5+4）×2÷2=6.5×2÷2=6.5（平方厘米）答：梯形的面积是6.5平方厘米五、解决问题33.解：3.9公顷=39000平方米,39000÷80=487.5（米）答：底是487.5米.34.解： 48×24-48×2=48×（24-2）=48×22=1056（平方米）答：苗圃的实际面积是1056平方米.35. 解：50×24÷3=1200÷3=400（棵）答：这块地可以种400棵荔枝树.36. 解：93×15÷4.5=1395÷4.5=310（棵）答：这块土地一共能栽310棵果树.37. 解：2.4×0.5×39=1.2×39≈47(千克)答：这块钢板大约重47千克.38. 解：面积变小了.理由：长方形的面积等于长乘宽,长方形拉成四边形,长和底相等,但是平行四边形的高比长方形的宽短.。

平行四边形面积公式解题技巧
解决平行四边形面积问题的技巧包括了解面积公式和应用基本
几何原理。

平行四边形的面积公式是，面积 = 底边长× 高，其中
底边长是平行四边形的一条底边的长度，高是从这条底边到与之平
行的另一条边的垂直距离。

下面我将详细解释如何使用这个公式以
及一些解题技巧。

首先，要确定平行四边形的底边长和高。

底边长通常是已知的，而高可能需要通过一些几何推理来确定。

如果高不是直接给出的，
你可以使用垂直平行边的性质来找到它。

另外，如果平行四边形是
由两个相等的三角形组成的话，可以利用三角形的性质来找到高。

其次，将已知的底边长和高代入面积公式中进行计算。

确保单
位是一致的，如果底边长是以厘米表示，那么面积就是平方厘米。

进行计算时要小心不要弄错单位。

此外，还有一些特殊情况需要特别注意。

如果平行四边形是菱形，那么它的面积公式可以简化为对角线之积的一半。

另外，如果
平行四边形是由两个相等的直角三角形组成的话，可以利用直角三
角形的性质来求解。

最后，要注意检查计算结果是否合理。

面积不可能是负数，如果计算结果为负数，那么可能是计算过程中出现了错误。

另外，面积也不可能超过平行四边形的周长，所以要确保计算结果在合理范围内。

总的来说，解决平行四边形面积问题的关键是熟练掌握面积公式，并且灵活运用基本的几何原理来确定底边长和高。

同时要注意特殊情况的处理，并且在计算过程中保持小心谨慎，确保结果的准确性和合理性。

希望这些技巧对你有所帮助。

平行四边形面积的计算练习题课堂练习（一）1. 填空在下面图形中, 与阴影部分面积相等的平行四边形有( )2. 一个平行四边形, 底是1.2米, 高是底的1.5倍, 求它的面积．3. 一块平行四边形钢板, 底5米, 高3米, 如果1平方米钢重39千克, 这块钢板重多少千克?4. 下图中的正方形周长为28厘米, 求平行四边形的面积．5. 一个平行四边形的底是9.6分米, 高2.5分米, 它的面积是多少平方分米?课堂练习（二）1. 单选图中, 甲和乙的面积相比较． [ ]A. 甲>乙B. 甲<乙C. 甲=乙D. 无法确定2. 一块平行四边形木板, 它的底是12分米, 高是8分米, 这块木板的面积是多少平方分米?3. 一块平行四边形的草坪, 已知它的面积是1050平方米, 高是25米, 这块草坪的底边长是多少米?4. 一块平行四边形地, 底23米, 高15米, 如果每平方米栽瓜秧9棵, 共栽多少棵?5. 平行四边形的高是70.2厘米, 是底的2倍, 平行四边形的面积是多少?课堂练习（三）1. 单选将一个平行四边形铁丝圈, 拉成一个长方形后, 面积____原来平行四边形的面积． [ ]A.等于B.大于C.小于2. 计算下面图形的面积．(单位：厘米)3. 一个平行四边形, 高3.6分米, 比底短14厘米, 它的面积是多少平方厘米?4. 一个平行四边形的面积是72平方分米, 已知底是9分米, 高是多少?5. 有一块平行四边形麦地, 底50米, 高是38米, 如果共收获小麦798千克, 平均每公顷收获小麦多少千克?课堂练习（四）1. 3.2公顷=( )平方米7.5平方米=( )平方米( )平方分米2. 某农民开垦一块底是36米, 高是30米的平行四边形地, 今年一共收小麦810千克, 平均每平方米产小麦多少千克?3. 一块面积是1900平方米的平行四边形地的底是76米, 求这块地的高．4. 有一块平行四边形的向日葵地, 已知高是28米, 底比高的2倍还多8米, 这块向日葵地的面积是多少平方米?5. 一个平行四边形, 它的底边减少6分米后还剩余18分米, 面积因此而减少72平方分米, 这个平行四边形原来的面积是多少平方分米?。

平行四边形的面积计算平行四边形是几何学中的常见图形，它具有特殊的性质和计算面积的方法。

在本文中，将介绍平行四边形的定义、性质以及计算面积的公式和步骤。

一、平行四边形的定义平行四边形是一个具有两对平行边的四边形。

它的对边分别平行且相等。

根据这个定义，我们可以得出平行四边形的性质和特点。

1. 对边性质：平行四边形的对边是平行的，并且对边长度相等。

2. 对角线性质：平行四边形的对角线相交于各自的中点，且对角线互相平分。

3. 顶点角性质：平行四边形的相邻顶点所对的角互补，即它们的和为180度。

二、平行四边形的面积计算公式平行四边形的面积可以用公式来计算。

该公式如下：面积 = 底边长度 ×高其中，底边长度是平行四边形的一条边的长度，高是从该边所在的顶点到对边的垂直距离。

三、计算平行四边形的面积步骤下面将介绍计算平行四边形面积的具体步骤。

步骤一：确定底边长度根据题目或给定图形，确定平行四边形的底边长度。

步骤二：确定高度确定从底边所在顶点到对边的垂直距离，该距离即为平行四边形的高。

步骤三：应用面积公式将底边长度和高代入平行四边形的面积公式，进行计算。

步骤四：得出结果进行具体计算，得到平行四边形的面积。

确保单位与题目要求一致。

示例：假设平行四边形的底边长度为5cm，高度为8cm，我们可以按照上述步骤计算。

步骤一：底边长度为5cm。

步骤二：高度为8cm。

步骤三：应用面积公式进行计算。

面积 = 5cm × 8cm = 40cm²步骤四：得到面积结果为40cm²。

结论：经过计算，该平行四边形的面积为40cm²。

总结：平行四边形的面积计算方法是利用底边长度和高的乘积来求解。

根据题目给出的数据，按照上述步骤进行计算即可得到结果。

熟练掌握平行四边形的面积计算方法对于解决几何题目和实际问题都具有重要意义。

通过不断练习和加深理解，我们可以更好地掌握平行四边形及其他几何图形的性质和计算方法。

平行四边形求阴影部分面积的题平行四边形求阴影部分面积的题一、问题描述在计算平行四边形的面积时，经常会遇到需要求解平行四边形阴影部分面积的问题。

在图形学、几何学或工程学等领域，常常需要根据给定的条件来计算平行四边形阴影部分的面积。

本文将围绕这一主题展开深入探讨，帮助读者全面理解和掌握相关知识。

二、基本概念1. 平行四边形是指具有两对对边分别平行的四边形。

在平行四边形中，对角线互相平分，且对角线所形成的两个三角形相等。

2. 阴影部分面积指的是在给定条件下，平行四边形中被其他图形或线段所遮挡的部分所形成的面积。

三、解题思路和方法在计算平行四边形阴影部分的面积时，可以采用以下解题思路和方法：1. 确定已知条件：首先需要明确已知条件，包括平行四边形的边长、对角线长、夹角大小等信息。

2. 绘制示意图：根据已知条件，绘制出平行四边形的示意图，标注出阴影部分以及其他相关线段或图形。

3. 利用几何知识：根据平行四边形的性质和几何知识，运用几何定理和公式进行推导和计算。

4. 分段计算：如果阴影部分的形状复杂，可以将其分割成若干个简单的几何图形，然后分别计算其面积，最后进行求和。

5. 检验结果：计算完成后，需要对结果进行检验，确保计算的正确性和准确性。

四、实例分析以具体的实例来说明如何计算平行四边形阴影部分的面积。

设平行四边形的对角线长分别为a和b，夹角为θ，现在需要计算阴影部分的面积。

解题步骤如下：1. 根据已知条件，利用平行四边形的性质和几何知识，可以推导出阴影部分的面积公式为S=(1/2)ab*sin(θ)。

2. 根据公式计算出阴影部分的面积，得到最终结果。

3. 确认计算结果的正确性，并对结果进行合理性检验。

五、个人观点和总结通过对平行四边形求阴影部分面积的题目进行深入探讨和分析，可以帮助我们更好地理解平行四边形的性质和面积计算方法。

在实际应用中，需要结合具体问题，合理运用几何知识和面积计算公式，才能准确求解平行四边形阴影部分的面积。