张量概念及其基本运算讲课讲稿
- 格式:ppt
- 大小:180.50 KB
- 文档页数:14

张量的运算方法**标题:张量的运算方法****一、引言**在许多数学和科学领域中,张量是一个重要的概念,它是一种多维数组,可以用于表示更复杂的数据结构。
张量的运算方法在数学、物理、计算机科学等领域中有着广泛的应用。
本篇文章将介绍张量的基本概念、运算规则以及一些常见的张量库。
**二、张量的基本概念**张量是一个可以表示任意维数数组的概念,它可以是一阶张量、二阶张量、高阶张量等。
在实际应用中,通常需要用到更高阶的张量,因为它们可以更好地表示复杂的数据结构。
**三、张量的基本运算**1. **标量与张量的乘法**:标量与一阶张量相乘,等同于将标量加在一阶张量上。
对于二阶或更高阶的张量,需要将标量与每一行或每列的对应元素相乘再相加。
2. **矩阵与张量的乘法**:矩阵与一阶或二阶张量相乘时,其结果为对应元素相乘后加在一阶或二阶张量的结果。
对于更高阶的张量,矩阵的乘积并不总是存在,取决于矩阵是否是子式的主对角线对称的幂。
3. **向量与张量的点积**:一维向量与一阶或二阶张量相乘,其结果为一维向量中每个元素与对应元素相乘后的和。
4. **张量的加法和减法**:同维度的张量可以相加或相减,执行这些操作时,需要考虑数据的一致性。
5. **张量的转置**:对于二阶或更高阶的张量,其转置是将主对角线上的元素与另一侧的对应元素交换位置。
对于一阶和二阶张量,转置操作还可以通过矩阵乘法实现。
6. **张量的共轭**:对于复数张量,可以通过取共轭来改变其复数元素的符号。
**四、常见张量库介绍**在Python中,有许多库可以用于处理和操作张量。
其中最常用的包括NumPy、TensorFlow和PyTorch等。
这些库提供了丰富的函数和方法来进行张量的创建、操作和运算。
**五、实例分析**以下是一个简单的例子,展示如何使用NumPy库进行一维张量的运算:```pythonimport numpy as np# 创建一个一维张量tensor = np.array([1, 2, 3])print("原始一维张量:", tensor)# 对一维张量进行加法和乘法运算result_add = tensor + 2 # 加法运算result_mul = tensor * 3 # 乘法运算print("加法运算结果:", result_add)print("乘法运算结果:", result_mul)```此外,我们还可以使用TensorFlow或PyTorch库来进行更高级的张量运算,例如矩阵乘法、向量化操作等。




§1 张量的定义张量:在三维笛卡儿〔Descartes〕坐标系中,一个含有三个与坐标相关的独立变量集合,通常可以用一个下标表示。
例如,对于位移分量u,v,w可以表示为u1,u2,u3,缩写记为u i,i=1, 2, 3。
对于坐标x,y, z可以表示为x i。
对于一个含有九个独立变量的集合,可以用两个下标来表示。
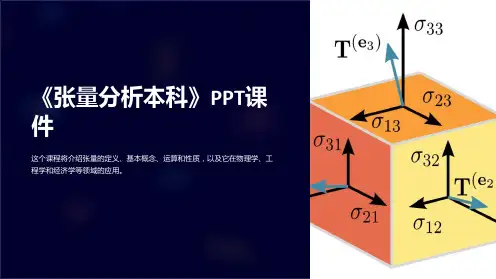
例如九个应力分量或应变分量〔由于对称,实际独立的仅有六个〕可以分别表示为σij和εij,其中σ11 , σ22分别表示σx, σxy〔就是τxy);ε11 , ε22分别表示εx,εxy(〕等。
同样,一个含有27个独立变量的集合可以用三个下标表示;而含有81个独立变量的集合可以用四个下标表示,依次可以类推。
为了给张量一个确切的定义,首先讨论矢量定义。
在坐标系Ox1x2x3中。
矢量OP的三个分量ζ 1, ζ 2,ζ3可以缩写作ζ i,同一矢量OP在新坐标系Ox'1x'2x'3中,写作ζ '1,ζ '2,ζ '3,缩写为ζ'i。
设坐标系Ox1x2x3与Ox'1x'2x'3的夹角方向余弦如下表所示方向余弦n i'j的第一下标对应于新坐标轴,而第二下标对应于原坐标轴。
则矢量在新老坐标系中的关系为或者上式可以缩写为或者。
a2, a3)和OP(ζ1, ζ2, ζ3),作它们的标量积,则考察矢量A(a1,显然,此标量积与坐标轴的选取无关,如果上述矢量作坐标变换,则反之,如ζ ' 为已知矢量,而a i为与坐标有关的三个标量,使一次形式在坐标变换时保持不变。
根据矢量定义,则a i 也是矢量。
推广上述的命题,可以给张量一个解析的定义。
设(ζ 1, ζ 2, ζ3)和(η 1, η 2, η3)是矢量,a ij是与坐标有关的九个量,假设当坐标变换时,双一次形式保持不变,则称由两个下标i,j确定的九个量的集合a ij为二阶张量。


张量与张量积的定义与计算张量是现代数学与物理学中非常重要的概念。
它广泛应用于各个领域,包括线性代数、微积分、物理学、工程学等。
在本文中,我们将介绍张量的基本概念、定义以及张量积的计算方法。
一、张量的定义张量可以看作是向量和矩阵的推广。
在物理学和工程学中,张量用于描述空间中的物理量。
在数学上,张量可以定义为多维数组,在不同的坐标系下有不同的分量表示。
在线性代数中,张量的定义可以从张量空间的角度看待。
假设V是一个n维向量空间,那么V的p阶张量空间可以表示为V ⊗ V ⊗⋯⊗V(一共p个V)。
其中⊗表示张量积,它是一种多重线性映射的二元运算。
二、张量积的定义张量积是以外积的方式组合两个向量的操作。
设有两个向量a和b,它们的张量积可以表示为a⊗b。
具体来说,张量积的结果是一个矩阵,其中每个元素由两个向量的对应元素相乘而得。
如果a是一个m维列向量,b是一个n维行向量,那么a⊗b的结果是一个m×n的矩阵。
矩阵中的每个元素由a和b的对应元素相乘得到。
三、张量积的计算计算张量积需要按照一定的规则进行。
具体来说,如果矩阵a和矩阵b的大小分别是m×n和p×q,那么它们的张量积可以通过以下步骤计算:1. 创建一个大小为(m×p)×(n×q)的零矩阵。
2. 遍历矩阵a的每个元素aij。
3. 将矩阵b的每个元素乘以aij,并将结果放入零矩阵中对应的位置。
计算完所有的元素后,得到的零矩阵就是矩阵a和矩阵b的张量积。
四、应用场景张量和张量积在各个领域都有重要的应用。
例如,在物理学中,张量用于描述力、能量、电磁场等物理量。
在工程学中,张量可用于描述应力、应变、磁场等。
此外,张量积还在机器学习和神经网络中扮演重要的角色。
在深度学习中,神经网络的参数可以表示为张量,通过计算张量积可以进行复杂的运算。
总结:本文介绍了张量与张量积的定义与计算方法。
张量是一种多维数组,在物理学和工程学中被广泛应用。

