分式方程的增根与无解

分式方程的增根和无解
增根和无解是分式方程中常见的两种情况。

增根是指分式方程化为整式方程后，产生的使分式方程的分母为$0$的根。

分式方程的增根问题是分式方程去分母的过程中，方程两边同乘了一个能使最简公分母为零的整式，致使未知数的取值范围扩大。

无解是指分式方程本身就是一个矛盾等式，不论未知数取何值都不能使方程两边的值相等。

分式方程无解包括两种情况：一种情况是分式方程变形后，整式方程本身无解；另一种情况是整式方程有解，但这个解使原方程的分母为$0$，即为分式方程的增根，所以原分式方程无解。

总的来说，分式方程的增根和无解是两个不同的概念，增根是分式方程的一种特殊情况，而无解则是分式方程的一种极端情况。

【八年级】浅谈分式方程的增根与无解在学习分式方程时，增根与无解是避不开的话题，也是绝大部分同学弄不清楚的地方。

今天，给大家带来 2 类典型的问题。

一、解分式方程时，增根是如何产生的？增根到底有多少个？二、增根与无解到底有怎样的区别与联系。

1.有关增根的问题1.1增根是如何产生的先看一个有意思的问题：x-1=0显然，我们都知道原方程的解为 x=1，但是如果我们没有直接移项，而是在方程的两边同时乘以 x，则原方程可化为 x(x-1)=0，可解得 x=0 或x=1.我们当然知道第一种方法是正确的，但是为什么我在等号两边同时乘了一个 x，就会变成两个解呢？这是因为两边同时乘的这个 x，我们没有确保它是不等于 0 的。

换言之，第二种解法的 x=0 就是这个一元一次方程的增根。

因为我在方程 x-1=0 两边同时乘以 x 后，得到的方程 x(x-1)=0 与原方程不是同解方程。

而我们解分式方程时，总是将分式方程化成整式方程进行求解。

由于这个过程扩大了原来末知数的取值范围，使得所化成的整式方程与原分式方程不是同解方程，带来了可能使所化成的整式方程成立，而使原分式方程分母为零的末知数的值，也即增根。

1.2增根到底有多少个再看一个有意思的问题，也是以前很多老师争论不休的问题。

故原方程无解，因此原方程的增根有 0 个。

这个问题为什么会产生歧义呢？这个方程的增根到底有几个？解法一、二、三到底哪个是正确的？首先，需要明确一点：解所有不含参数的分式方程，按照所有项移到方程左边，进而通分，这样的方式解得的分式方程永远都不会有增根，即解法三这样的。

因为这种解法，一直在进行等价转化，即都是同解方程。

那既然这种解法不会产生增根，为什么教材不提倡这种做法呢？笔者觉得原因有两个。

一、通过通分化简求值的方法相比于去分母化成整式方程更加麻烦，虽然不需要验根，但是对于复杂一些的分式方程，通分的计算量不小。

二、更重要的一点，通分的方法无法处理含参数的分式方程。

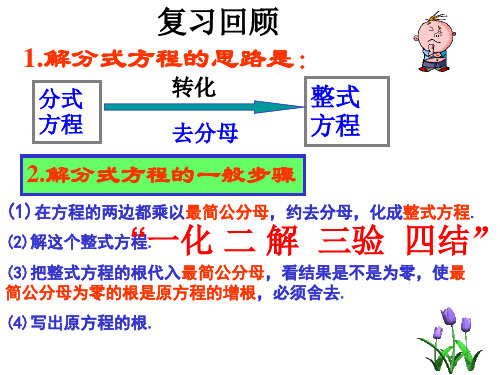
分式方程有增根、无解等问题【真题演练】1．（2021秋•德江县期末）关于x的方程有增根，则m的值是（）A．0B．2或3C．2D．32．（2021秋•开福区校级期末）若关于x的分式方程有增根，则m的值是（）A．m＝2或m＝6B．m＝2C．m＝6D．m＝2或m＝﹣63．（2021秋•庄浪县期末）若关于x的方程＝2有增根，则m的取值是（）A．0B．2C．﹣2D．14．（2021秋•黔西南州期末）若关于x的方程+2＝有增根，则m的值是（）A．﹣2B．2C．1D．﹣15．（2022春•原阳县月考）分式方程+2＝有增根，则m＝．6．（2022春•靖江市校级月考）已知关于x的分式方程有增根，则m＝．7．（2021秋•新田县期末）解关于x的分式方程＝时不会产生增根，则m的取值范围是．8．（2021秋•平江县期末）若关于x 的分式方程有增根，则m 的值是 ．【真题演练】9．（2022春•江都区校级月考）若关于x 的分式方程无解，则实数a 的值为（ ） A ．7B ．3C ．3或7D ．±710．（2022春•西峡县校级月考）若关于x 的分式方程无解，则m 的值为（ ） A ．﹣6B ．﹣10C ．0或﹣6D ．﹣6或﹣1011．（2021春•南召县期中）若关于的x 方程无解，则a 的值为（ ） A ．或B ．0或3C ．或3 D ．0或12．（2021秋•晋安区期末）若关于x 的分式方程＝无解，则k 的值为（ ） A ．1或4或﹣6B ．1或﹣4或6C ．﹣4或6D ．4或﹣613．（2021秋•两江新区期末）若关于x 的方程＝1无解，则a ＝（ ） A ．3B ．0或8C ．﹣2或3D ．3或814．（2021秋•官渡区期末）若关于x的方程无解，则a的值为（）A．2B．C．1或2D．2或15．（2022•南海区一模）若关于x的方程无解，则a ＝．16．（2021秋•虎林市校级期末）若关于x 的分式方程无解，则a 的值为（）A．﹣2B．1C．﹣2或1D．1或0【真题演练】17．（2022春•海陵区校级月考）关于x的方程有正数解，则m取值范围是．18．（2022•禅城区一模）若关于x的分式方程＝有正整数解，则整数m为．19．（2022•仁寿县模拟）已知关于x的方程＝5的解不是正数，则m的取值范围为．20．（2022•任城区一模）关于x的分式方程的解是正数，则a的取值范围是．21．（2021秋•北安市校级期末）关于x的方程的解不小于1，则m的取值范围为．22．（2021秋•绵阳期末）若关于x的方程的解为整数，则满足条件的所有整数a的和等于．23．（2022春•普宁市校级月考）若分式方程的解为整数，则整数a＝（）A．a＝±2B．a＝±1或a＝±2C．a＝1或2D．a＝±124．（2021秋•南沙区期末）若正整数m使关于x的分式方程的解为正数，则符合条件的m的个数是（）A．2B．3C．4D．525．（2021秋•合川区期末）若a≥﹣4，且关于x的分式方程+3＝有正整数解，则满足条件的所有a的取值之积为．。

怎样区别分式方程的增根与无解责旧.蝙辑:王二喜刘顿学习了解分式方程以后,不少同学把增根与无解混为一谈.为了掌握这两个概念,现举例说明这两个概念的区别和联系.一.岔将分式方程变形为整式方程时,方程两边同乘以一个含有未知数的整式,并约去分母,可能产生不适合原分式方程的解或根,这种根称为增根.如,若方程—+3=有增根,则这个增根一定是=2.一二_徭绣罗解分式方程的关键是去分母将分式方程转化为整式方程.对原分式方程的解来说,各分式的分母不能为零,而对去分母后得到的整式方程来说,没有这个限制.因此,解分式方程时,必须检验.2O09.3的增根与无解怎样区剔分式方程课程_IiI赍源_…i庭裔锄辑分式方程无解有两种情形:一种是将原分式方程两边都乘以最简公分母,去分母并整理得到的整式方程为ax=b,若a=O,而b≠0,则此整式方程无解,即原分式方程无解;另一种是化分式方程为整式方程,整式方程的解是原分式方程的增根,此时分式方程无鳃.,ll如,若关于的方程一1=0无解,试求n的值.将原方程去分母转化为(o一1)x+2=O,即(n一1)一2.当n一1=0时,~Ja=l,此时整式方程无解.所以当n=1时,原方程无解.对于方程(.～1)x+2=O,当=1时,原方程无解.所以当(n一1)×1+2=0时,即o=一1,原方程无解.所以a为1或一1.在解本题时,考虑问题要全面,不要只考虑原分式方程有增根的情形,而忽略了整式方程无解,则原分式方程无解的情况.一分薅方癌警车麟按哮暴分式方程有增根,则增根是原分式方程变形后所得整式方程的根,但不是原分式方程的根,即这个根使最简公分母为0.如,解分式方程=3一刍,可得x=2,把=2代人(2一),得2一x=O,即=2使分式方程的分母2一为0.所以x=2不是原方程的解,x=2 是原方程的增根,此方程无解.在本题中,分式方程有增根,方程无解.请思考下面两道题:1.若关于的方程:m无解,求m的值.2.m为何值时,关于的方程+x2-4=会产生增根.目I2OO9.3。

分式方程的增根与无解分式方程的增根与无解是分式方程中常见的两个概念，同学们在学习分式方程后，常常会对这两个概念混淆不清，认为分式方程无解和分式方程有增根是同一回事，事实上并非如此．分式方程有增根，指的是解分式方程时，在把分式方程转化为整式方程的变形过程中，方程的两边都乘了一个可能使分母为零的整式，从而扩大了未知数的取值范围而产生的未知数的值；而分式方程无解则是指不论未知数取何值，都不能使方程两边的值相等．它包含两种情形：（一）原方程化去分母后的整式方程无解；（二）原方程化去分母后的整式方程有解，但这个解却使原方程的分母为0，它是原方程的增根，从而原方程无解．现举例说明如下：例1 解方程2344222+=---x x x x ． ① 解：方程两边都乘以（x+2）（x-2），得2（x+2）-4x=3（x-2）．②解这个方程，得x=2．经检验：当x=2时，原方程无意义，所以x=２是原方程的增根．所以原方程无解．【说明】显然，方程①中未知数x 的取值范围是x ≠2且x ≠-2．而在去分母化为方程②后，此时未知数x 的取值范围扩大为全体实数．所以当求得的x 值恰好使最简公分母为零时，x 的值就是增根．本题中方程②的解是x ＝2，恰好使公分母为零，所以x ＝2是原方程的增根，原方程无解．例2 解方程22321++-=+-xx x x ． 解：去分母后化为x －1＝3－x ＋2（2＋x ）．整理得0x ＝8．因为此方程无解，所以原分式方程无解．【说明】此方程化为整式方程后，本身就无解，当然原分式方程肯定就无解了．由此可见，分式方程无解不一定就是产生增根．例3（2007湖北荆门）若方程32x x --=2m x-无解，则m=——————． 解：原方程可化为32x x --=－2m x -． 方程两边都乘以x －2，得x －3=－m ．解这个方程，得x=3－m ．因为原方程无解，所以这个解应是原方程的增根．即x=2，所以2=3－m ，解得m=1．故当m=1时，原方程无解．【说明】因为同学们目前所学的是能化为一元一次方程的分式方程，而一元一次方程只有一个根，所以如果这个根是原方程的增根，那么原方程无解．但是同学们并不能因此认为有增根的分式方程一定无解，随着以后所学知识的加深，同学们便会明白其中的道理，此处不再举例．例4当a 为何值时，关于x 的方程223242ax x x x +=--+①会产生增根？ 解：方程两边都乘以（x+2）（x-2），得2（x ＋2）＋ax ＝3（x －2）整理得（a －1）x ＝－10 ②若原分式方程有增根，则x ＝2或－2是方程②的根．把x ＝2或－2代入方程②中，解得，a ＝－4或6．【说明】做此类题首先将分式方程转化为整式方程，然后找出使公分母为零的未知数的值即为增根，最后将增根代入转化得到的整式方程中，求出原方程中所含字母的值．若将此题“会产生增根”改为“无解”，即：当a 为何值时，关于x 的方程223242ax x x x +=--+①无解？ 此时还要考虑转化后的整式方程（a －1）x ＝－10本身无解的情况，解法如下：解：方程两边都乘以（x+2）（x-2），得2（x ＋2）＋ax ＝3（x －2）整理得（a －1）x ＝－10 ②若原方程无解，则有两种情形：（1）当a －1＝0（即a ＝1）时，方程②为0x ＝－10，此方程无解，所以原方程无解。

分 式 方 程 的 增 根 与 无 解 讲 解例1解方程—24x 3•①x 2 x 4 x 2解：方程两边都乘以(x+2) (x-2 )，得2 (x+2) -4x=3 (x-2 ).②解这个方程，得x=2.经检验：当x=2时，原方程无意义，所以x=2是原方程的增根.所以原方程无解.例2解方程x 13 x2 .x 22 x解：去分母后化为x — 1 = 3— x + 2 (2+ x ).整理得0x = 8.因为此方程无解，所以原分式方程无解.例3 (2007湖北荆门)若方程 王卫二―丄无解，则m= ------------ .x 22 x解：原方程可化为x 3二—m.x 2 x 2方程两边都乘以x — 2，得x — 3=— m解这个方程，得x=3— m因为原方程无解，所以这个解应是原方程的增根.即 x=2，所以2=3— m 解得m=1.故当m=1时，原方程无解.ax例4当a为何值时，关于x的方程齐厂齐①会产生增根?解：方程两边都乘以(x+2) (x-2 ),得 2 (x + 2)+ ax= 3 (x —2)整理得(a—1) x = —10若原分式方程有增根，则x= 2或-2是方程②的根.把x = 2或一2代入方程②中，解得，a = —4或6.若将此题“会产生增根”改为“无解”，即:2 ax 3当a为何值时，关于x的方程厂2 厂门①无解?此时还要考虑转化后的整式方程（a—1）x二—10本身无解的情况，解法如下:解：方程两边都乘以(x+2) (x-2 ),得 2 (x + 2)+ ax= 3 (x —2)整理得(a—1) x = —10若原方程无解，则有两种情形:（1）当a—1 = 0 （即a= 1）时，方程②为0x =一10，此方程无解，所以原方程无解。

（2）如果方程②的解恰好是原分式方程的增根，那么原分式方程无解•原方程若有增根，增根为x = 2或一2,把x = 2或一2代入方程②中，求出a= —4或6.综上所述，a= 1或a = —4或a=6时，原分式方程无解.例5: （2005扬州中考题）6A 、0B 、1C 、-1D 、1 或-1分析：使方程的最简公分母(x+1)(x-1)=0 则x=-1或x=1，但不能忽略增根除满足最简公 分母为零,还必须是所化整式方程的根。

含字母参数分式方程的有增根、有解和无解问题【要点梳理】要点一 分式方程的增根分式方程有增根，指的是解分式方程时，在把分式方程转化为整式方程的变形过程中，方程的两边都乘了一个可能使分母为零的整式，从而扩大了未知数的取值范围而产生的未知数的值；要点二 分式方程的无解而分式方程无解则是指不论未知数取何值，都不能使方程两边的值相等．它包含两种情形：（一）原方程化去分母后的整式方程无解；（二）原方程化去分母后的整式方程有解，但这个解却使原方程的分母为0，它是原方程的增根，从而原方程无解.【典型例题】类型一、概念理解1.分式方程的增根概念：把分式方程化为整式方程后，得到的整式方程的根使分式方程中分母的值为0，分式方程无解，这样的根叫做________．检验方法：将解得的整式方程的根代入最简公分母，看计算结果是否为0，不为0就是原分式方程的根，若为0则为增根，必须舍去．【答案】增根解：把分式方程化为整式方程后，得到的整式方程的根使分式方程中分母的值为0，分式方程无解，这样的根叫做增根，故答案为：增根．2.分式方程有增根与分式方程无解的关系：分式方程的增根与无解并非同一个概念，分式方程无解，可能是解为增根，也可能是去分母后的整式方程无解．分式方程的增根是去分母后的________方程的根，也是使________方程的分母为0的根．【答案】 整式 分式分式方程的增根是去分母后的整式方程的根，也是使分式方程的分母为0的根．故答案为：整式，分式类型二、含参分式方程的增根3、关于x 的方程225111m x x x +=+--去分母转化为整式方程后产生增根，求m 的值． 【答案】－10或－4【分析】方程两边同时乘以21x -将分式方程化为整式方程，再将整式方程的增根代入整式方程中计算求解即可.解：方程两边同乘以21x -，得2(1)5(1)x x m --+=，当210x -=时，1x =±，∴关于x 的方程225111m x x x +=+--的增根为±1， 当1x =时，2(11)5(11)10m =--+=-；当1x =-时，2(11)5(11)4m =----+=-，故m 的值为10-或4-．【点拨】本题主要考查分式方程的增根，解题的关键是理解增根产生的原因，并能从整式方程中代入增根求解对应参数.举一反三：【变式1】如果解关于x 的分式方程1134x m x x +-=-+出现了增根，求m 的值． 【答案】-3【分析】分式方程的增根是分式方程转化为整式方程的根，且使分式方程的分母为0的未知数的值． 解：由分式方程1134x m x x +-=-+去分母， 整理得（m+2）x=-4m-15，由分母可知，分式方程的增根可能是3或-4，当x=3时，（m+2）×3=-4m-15，解得m=-3， 当x=-4时，（m+2）×（-4）=-4m-15，此方程无解．故m 的值为-3．【点拨】本题考查了分式方程的增根．增根问题可按如下步骤进行：①让最简公分母为0确定增根；②化分式方程为整式方程；③把增根代入整式方程即可求得相关字母的值．【变式2】已知关于x 的方程214339m m x x x +-=+--． （1）若m ＝﹣3，解这个分式方程；（2）若原分式方程无解，求m 的值．【答案】（1）x ＝5.5；（2）m ＝﹣1，m ＝2，m ＝﹣47． 【分析】（1）把m ＝−3代入原方程得23134339x x x -+-=+--，方程两边都乘最简公分母（x −3）（x ＋3），可以把分式方程转化为整式方程求解； （2）方程两边都乘最简公分母（x −3）（x ＋3），分式方程转化为整式方程，m （x −3）＋（x ＋3）＝m ＋4，整理得（m ＋1）x ＝1＋4m ，原分式方程无解，m ＋1＝0，m ＝−1，然后把x ＝3．x ＝−3分别代入整式方程求m 值．解：（1）依题意把m ＝﹣3代入原方程得23134339x x x --+-=+--． 方程两边都乘最简公分母（x ﹣3）（x +3）得，﹣3（x ﹣3）+（x +3）＝1，解得x ＝5.5，检验：把x ＝5.5代入（x +3）（x ﹣3）≠0．∴x ＝5.5是原方程的解；（2）当（x +3）（x ﹣3）＝0时．x ＝±3． 方程两边都乘最简公分母（x ﹣3）（x +3），得，m （x ﹣3）+（x +3）＝m +4，整理得（m +1）x ＝1+4m ，∵原分式方程无解．∴m +1＝0，m ＝﹣1．把x ＝±3代入m （x ﹣3）+（x +3）＝m +4． m ＝2，m ＝﹣47． ∴m ＝﹣1，m ＝2，m ＝﹣47． 【点拨】分式方程转化为整式方程求解，最后注意需检验．无解注意整式方程一次项系数带字母系数，字母系数为零，再把增根代入化简的整式方程，这样不漏m 的值．类型三、含参分式方程的有解、无解问题4、若关于x 的分式方程212111m x x x -=--+无解．求m 的值． 【答案】2或－4【分析】分式方程去分母转化为整式方程，根据分式方程无解得到x ＝1或−1，代入整式方程即可求出m 的值．解：分式方程两边同乘（x ＋1）（x −1），去分母得：m －（x ＋1）＝2（x −1），整理得：3x ＝m ＋1，由分式方程无解得到x −1＝0，或x ＋1＝0，即x ＝1或−1，代入整式方程得：m ＝2或－4．【点拨】此题考查了分式方程的解，解决本题的关键是熟记分式方程无解即最简公分母为0．举一反三：【变式1】关于x 的分式方程3601(1)x k x x x x ++-=--有解，则k 该满足什么条件？ 【答案】3k ≠-且5k ≠.【分析】根据分式方程有解的条件进行求解即可；解：方程去分母得：()()3160x x x k -+-+=，去括号得：3360x x x k -+--=，移项、合并得：83x k =+，∵该分式方程有解，∴0x ≠且1x ≠，即30k +≠，且38k +≠，解得：3k ≠-目5k ≠．【点拨】本题主要考查了分式方程有解的相关计算，准确分析计算是解题的关键．【变式2】若关于x 的方程：234393ax x x x +=--+无解，求a 的值． 【答案】a ＝1或8或﹣6．【分析】分式的无解分两种情况来解：（1）是分式有增根，即分母为零；（2）是分式方程转化成整式方程后，整数方程无解，即未知数系数为0．解：分式方程去分母得：3x +9+ax ＝4x ﹣12，（1）由分式方程有增根，得到（x +3）（x ﹣3）＝0，即x ＝3或x ＝﹣3，把x ＝3代入整式方程得：18+3a ＝0，即a ＝﹣6；把x ＝﹣3代入整式方程得：﹣3a ＝﹣24，即a ＝8，综上，a 的值为﹣6或8．（2）整式方程整理得：（a ﹣1）x ＝﹣21，由方程无解，得到a ﹣1＝0，即a ＝1或8或﹣6．【点拨】注意区分分式方程无解和有增根两种情况．分式方程无解包括有增根和化成整数方程后无解的情况，而有增根仅仅是分式分母为0一种情形．类型四、分式方程的增根和无解综合5、有下列说法：①不论k 取何实数，多项式x 2﹣ky 2总能分解能两个一次因式积的形式；②关于x 的分式方程3122++=--x m x x 无解，则m ＝1；③关于x 、y 的方程组252ax y x ay a +=-⎧⎨-+=⎩，将此方程组的两个方程左右两边分别对应相加，得到一个新的方程，其中，当a 每取一个值时，就有一个方程，而这些方程有一个公共解，则这个公共解为31x y =⎧⎨=-⎩，其中正确的是____．（填序号） 【答案】②③【分析】分别运用因式分解的公式法、分式方程的解法及解二元一次方程组的方法，可作出判断． 解：①当k 为负值时，多项式x 2﹣ky 2不能分解能两个一次因式积的形式，故①不正确；②将关于x的分式方程3122++=--x mx x两边同时乘以（x﹣2）得3﹣x﹣m＝x﹣2∴x＝52m，∵原分式方程无解，∴x＝2，∴52m＝2，解得m＝1，故②正确；③将所给方程组的两个方程左右两边分别对应相加，得（a﹣1）x+（a+2）y＝2a﹣5，（x+y）a+2y﹣x＝2a﹣5，∴225x yy x+=⎧⎨-=-⎩，解得：31 xy=⎧⎨=-⎩则当a每取一个值时，就有一个方程，而这些方程有一个公共解，则这个公共解为31xy=⎧⎨=-⎩，故③正确．综上，正确答案为：②③．【点拨】本题考查了因式分解、分式方程的解、二元一次方程组的解，解题关键是理解题意，遵循题意按照相应的解题方法准确进行计算．举一反三：【变式1】已知关于x的分式方程512x ax x+-=-．(1)若分式方程的根是5x=，求a的值；(2)若分式方程有增根，求a的值；(3)若分式方程无解；求a的值的．【答案】(1)1;(2)-2;(3)3或-2【分析】分式方程去分母转化为整式方程，（1）把x=5代入整式方程求出a的值即可；（2）由分式方程有增根，得到最简公分母为0求出x的值，代入整式方程求出a的值即可；（3）分a-3=0与a-3≠0两种情况，根据分式方程无解，求出m的值即可．解：(1)去分母得，x（x+a）-5（x-2）=x（x-2），整理得：(3)100a x -+=把x =5代入(3)100a x -+=得，5(3)100a -+=，∴a =1；(2) 由分式方程有增根，得到x （x -2）=0，解得：x=2或x=0，把x=2代入整式方程(3)100a x -+=得：a=-2；把x=0代入整式方程(3)100a x -+=得：a 的值不存在，∴分式方程有增根，a=-2(3) 化简整式方程得：（a -3）x =-10，当a -3=0时，该方程无解，此时a =3；当a -3≠0时，要使原方程无解，必须为分式方程增根，由（2）得：a =-2，综上，a 的值为3或-2．【点拨】此题考查了分式方程的解和增根，增根确定后可按如下步骤进行：①化分式方程为整式方程；②把增根代入整式方程即可求得相关字母的值．【变式2】已知W ＝（1122a a +-+）÷2244a a a -+． （1）化简W ；（2）若a ，2，4恰好是等腰△ABC 的三边长，求W 的值．（3）若12k W a +=+的解为正数，求k 的取值范围． 【答案】(1)22a a -+；(2)W 的值为13；(3)3k >-. 【分析】（1）先算括号里的，再运用完全平方公式进行化简即可得；（2）根据a ，2，4恰好是等腰△ABC 的三边长可得a ＝4，将a ＝4代入即可得；（3）根据题意得2122a k a a -+=++，解得3a k =+，根据12k W a +=+的解为正数得30k +>，进行计算即可得．(1)解：2112()2244a W a a a a =+÷-+-+ =2222(2)(2)(2)(2)(2)a a a a a a a a ⎡⎤+-+÷⎢⎥+-+--⎣⎦ =22(2)(2)(2)2a a a a a-+- =22a a -+ 解：∵a ，2，4恰好是等腰△ABC 的三边长，∴a ＝4，2422124263a W a --====++． (3) 解：由题意得，2122a k a a -+=++， 21a k -=+3a k =+ ∵12k W a +=+的解为正数， ∴30k +>，2320a k +=++≠3k >-．【点拨】本题考查了分式的化简求值，等腰三角形，分式方程，解题的关键是掌握这些知识点．【变式3】阅读下列材料：在学习“分式方程及其解法”的过程中，老师提出一个问题：若关于x 的分式方程14a x =-的解为正数，求a 的取值范围．经过独立思考与分析后，小明和小聪开始交流解题思路，小明说：解这个关于x 的方程，得到方程的解为4x a =+，由题目可得40a +>，所以4a >-，问题解决．小聪说：你考虑的不全面，还必须保证4a ≠-才行．(1)请回答：的说法是正确的，正确的理由是．完成下列问题：(2)已知关于x 的方程233m x x x -=--的解为非负数，求m 的取值范围； (3)若关于x 的方程322133x nx x x --+=---无解，求n 的值． 【答案】(1)小聪，分式的分母不能为0；(2)6m ≥-且3m ≠-；(3)1n =或53． 【解析】【分析】（1）根据分式有意义的条件：分母不能为0，即可知道小聪说得对；（2）首先按照解分式方程的步骤得到方程的解，再利用解是非负数即可求出m 的取值范围；（3）按照解分式方程的步骤去分母得到整式方程，若分式方程无解，则得到增根或者整式方程无解，即可求出n 的范围．(1)解：∵分式方程的解不能是增根，即不能使分式的分母为0∴小聪说得对，分式的分母不能为0．(2) 解：原方程可化为233m x x x +=-- 去分母得：2(3)m x x +=-解得：6x m =+∵解为非负数∴60m +≥，即6m ≥-又∵30x -≠∴63m +≠，即3m ≠-∴6m ≥-且3m ≠-(3) 解：去分母得：322(3)x nx x -+-=--解得：(1)2n x -=∵原方程无解∴10n -=或者3x =①当10n -=时，得：1n =②当3x =时，23(1)n =-，得：53n = 综上：当1n =或53n =时原方程无解．【点拨】本题考查了解分式方程以及根据分式方程的解确定参数范围，重点要掌握解分式方程的步骤：去分母化成整式方程；再解整式方程；验根．理解当分式方程无解时包含整式方程无解和有曾根两种情况．。