高三数学立体几何与空间向量

2023北京高三一模数学汇编空间向量与立体几何1．（2023·北京房山·统考一模）如图，已知正方体1111ABCD A B C D −，则下列结论中正确的是（ ）A ．与三条直线111,,AB CCD A 所成的角都相等的直线有且仅有一条 B ．与三条直线111,,AB CC D A 所成的角都相等的平面有且仅有一个 C ．到三条直线111,,AB CC D A 的距离都相等的点恰有两个 D ．到三条直线111,,AB CC D A 的距离都相等的点有无数个2．（2023·北京丰台·统考一模）如图，在直三棱柱111ABC A B C 中，AC BC ⊥，2AC =，1BC =，12AA =，点D 在棱AC 上，点E 在棱1BB 上，给出下列三个结论：①三棱锥E ABD −的体积的最大值为23；②1A D DB +③点D 到直线1C E ． 其中所有正确结论的个数为（ ） A ．0B ．1C ．2D ．33．（2023·北京西城·统考一模）如图，在棱长为2的正方体1111ABCD A B C D −中，点M ，N 分别在线段1AD 和11B C 上．给出下列四个结论： ①MN 的最小值为2； ②四面体NMBC 的体积为43； ③有且仅有一条直线MN 与1AD 垂直； ④存在点M ，N ，使MBN △为等边三角形． 其中所有正确结论的序号是____．4．（2023·北京海淀·统考一模）如图，直三棱柱111ABC A B C 中，1AC BC ==，12AA =，AC BC ⊥，D 是1AA 的中点．(1)证明：1C D ⊥平面BCD ；(2)求直线CD 与平面1BC D 所成角的正弦值．5．（2023·北京西城·统考一模）如图，在四棱锥P ABCD −中，PA ⊥平面ABCD ，//AB CD ，AB AD ⊥，1AB =，2PA AD CD ===．E 为棱PC 上一点，平面ABE 与棱PD 交于点F ．再从条件①、条件②这两个条件中选择一个作为己知，完成下列两个问题(1)求证：F 为PD 的中点； (2)求二面角B FC P −−的余弦值． 条件①：//BE AF ；条件②：BE PC ⊥．注：如果选择条件①和条件②分别解答，按第一个解答计分．6．（2023·北京丰台·统考一模）如图，在四棱锥P ABCD −中，底面是边长为2的菱形，AC 交BD 于点O ，60BAD ∠=︒，PB PD =．点E 是棱P A 的中点，连接OE ，OP ．(1)求证：//OE 平面PCD ；(2)若平面P AC 与平面PCD 知，求线段OP 的长．条件①：平面PBD ⊥平面ABCD ； 条件②：PB AC ⊥．注：如果选择条件①和条件②分别解答，按第一个解答计分．7．（2023·北京东城·统考一模）如图，在长方体1111ABCD A B C D −中，12AA AD ==，1BD 和1B D 交于点E ，F 为AB 的中点.(1)求证：EF ∥平面11ADD A ；(2)再从条件①、条件②这两个条件中选择一个作为已知，求 （i ）平面CEF 与平面BCE 的夹角的余弦值； （ii ）点A 到平面CEF 的距离. 条件①：1CE B D ⊥；条件②：直线1B D 与平面11BCC B 所成的角为4π. 注：如果选择条件①和条件②分别解答，按第一个解答计分.8．（2023·北京房山·统考一模）如图，四棱锥P ABCD −的底面是矩形，PD ⊥底面ABCD ，2PD DC AD ===，M 为BC 的中点.(1)求证：AM ⊥平面PBD ；(2)求平面ABCD 与平面APM 所成角的余弦值； (3)求D 到平面APM 的距离.9．（2023·北京朝阳·统考一模）如图，在三棱柱111ABC A B C 中，1AA ⊥平面ABC ，D ，E 分别为AC ，11A C的中点，AB BC ==12AC AA ==．(1)求证：AC ⊥平面BDE ；(2)求直线DE 与平面ABE 所成角的正弦值； (3)求点D 到平面ABE 的距离．10．（2023·北京石景山·统考一模）如图，在四棱锥P ABCD −中，底面ABCD 是边长为2的正方形，侧面PAD 为等腰直角三角形，且π2PAD ∠=，点F 为棱PC 上的点，平面ADF 与棱PB 交于点E .(1)求证：//EF AD ；(2)从条件①、条件②、条件③这三个条件中选择两个作为已知，求平面PCD 与平面ADFE 所成锐二面角的大小.条件①：AE =条件②：平面PAD ⊥平面ABCD ；⊥.条件③：PB FD注：如果选择的条件不符合要求，第（2）问得0分；如果选择多个符合要求的条件分别解答，按第一个解答计分.参考答案1．D【分析】所成的角都相等的直线有无数条，A 错误，成的角相等的平面有无数个，B 错误，距离相等的点有无数个，C 错误，D 正确，得到答案.【详解】对选项A ：根据对称性知1AC 与三条直线的夹角相等，则与1AC 平行的直线都满足条件，有无数条，错误；对选项B ：根据对称性知平面1A BD 与三条直线所成的角相等，则与平面1A BD 平行的平面都满足条件，有无数个，错误；对选项C ：如图所示建立空间直角坐标系，设正方体边长为1，()1,0,0A ，()1,1,0B ，1DB 上一点(),,P a a a ，则()0,1,0AB =，()1,,PA a a a =−，(cos ,AB PA AB PA AB PAa ⋅==⋅P 到直线AB的距离为21cos ,PA PA AB ⋅−==，同理可得P 到直线1CC 和11D A 1DB 上的点到三条直线111,,AB CC D A 的距离都相等，故有无数个，错误；对选项D ：1DB 上的点到三条直线111,,AB CC D A 的距离都相等，故有无数个，正确； 故选：D 2．C【分析】根据锥体的体积公式判断①，将将ABC 翻折到与矩形11ACC A 共面时连接1A B 交AC 于点D ，此时1A D DB +取得最小值，利用勾股定理求出距离最小值，即可判断②，建立空间直角坐标系，利用空间向量法求出点到距离，再根据函数的性质计算可得. 【详解】在直三棱柱111ABC A B C 中1BB ⊥平面ABC ，对于①：因为点E 在棱1BB 上112A B A B ==，所以[]0,2BE ∈，又13E ABD ABDV BE S−=⋅，又AC BC ⊥，2AC =，1BC =，点D 在棱AC 上，所以[]0,2AD ∈，[]110,122ABDSAD BC AD =⋅=∈，所以1233E ABD ABDV BE S−=⋅≤，当且仅当D 在C 点、E 在1B 点时取等号，故①正确； 对于②：如图将ABC 翻折到与矩形11ACC A 共面时连接1A B 交AC 于点D ，此时1A D DB +取得最小值，因为1112A C CC ==，1BC =，所以13BC =，所以1A B == 即1A D DB +对于③：如图建立空间直角坐标系，设(),0,0D a ，[]0,2a ∈，()0,1,E c ，[]0,2c ∈，()10,0,2C ，所以()1,0,2C D a =−，()10,1,2C E c =−，则点D 到直线1C E 的距离221111CD CE d C D C E ⎛⎫⋅ ⎪=−=⎪⎝⎭=当2c =时2d =≥， 当02c ≤<时()2024c <−≤，()21142c ≤−，()215142c +≥−，则()241601512c <≤+−，所以当()()224221c c −−+取最大值165，且20a=时min d = 即当D 在C 点E 在B 点时点D 到直线1C E ，故③正确；故选：C 3．①②④【分析】对于①，利用直线之间的距离即可求解；对于②，以M 为顶点，NBC 为底面即可求解；对于③，利用直线的垂直关系即可判断；对于④，利用空间坐标即可求解.【详解】对于①，由于M 在1AD 上运动，N 在11B C 上运动，所以MN 的最小值就是两条直线之间距离11D C ，而112D C =，所以MN 的最小值为2；对于②，111233M BNC BNC BNC V SD C S −=⋅⋅=⋅，而12222BNCS=⨯⨯=，所以四面体NMBC 的体积为43；对于③，由题意可知，当M 与1D 重合，N 与1C 重合时， 111D C AD ⊥，又根据正方体性质可知，111AD A B CD ⊥，所以当M 为1AD 中点，N 与1B 重合时，此时1MN AD ⊥，故与1AD 垂直的MN 不唯一，③错误；对于④，当MBN △为等边三角形时，BM BN =，则此时1AM B N =.所以只需要BM 与BN 的夹角能等于π3即可.以D 为原点，DA 、DC 、1DD 分别为x轴、y 轴、z 轴建立空间直角坐标系，如下图，设1AM B N n ==，则由题意可得2M ⎛⎝，()2,2,0B ，()2,2,2N n −，则可得BM ⎛=− ⎝，(),0,2BN n =−，则12cos2n BM BN MBN BM BN ⋅∠===⋅，整理可得2120n n ⎫−+=⎪⎪⎝⎭，该方程看成关于n的二次函数，44140⎫∆=−⨯⨯=>⎪⎪⎝⎭，所以存在n 使得MBN △为等边三角形. 故答案为：①②④ 4．(1)证明见解析(2)3【分析】（1）以点C 为坐标原点，CA 、CB 、1CC 所在直线分别为x 、y 、z 轴建立空间直角坐标系，利用空间向量法证明出1C D CB ⊥，1C D CD ⊥，再利用线面垂直的判定定理可证得结论成立； （2）利用空间向量法可求得直线CD 与平面1BC D 所成角的正弦值.【详解】（1）证明：在直三棱柱111ABC A B C 中，1CC ⊥平面ABC ，且AC BC ⊥，以点C 为坐标原点，CA 、CB 、1CC 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系，则点()0,1,0B 、()0,0,0C 、()10,0,2C 、()1,0,1D ，()0,1,0CB =、()1,0,1CD =、()11,0,1C D =−，所以，10CB C D ⋅=，11010CD C D ⋅=+−=，则1C D CB ⊥，1C D CD ⊥， 又因为CB CD C =，CB 、CD ⊂平面BCD ，因此，1C D ⊥平面BCD . （2）解：设平面1BC D 的法向量为(),,m x y z =，()10,1,2BC =−， 则11200m BC y z m C D x z ⎧⋅=−+=⎪⎨⋅=−=⎪⎩，取1z =，可得()1,2,1m =，所以，cos ,2CD m CD m CD m⋅===⋅ 因此，CD 与平面1BC D . 5．(1)证明见解析【分析】（1）若选条件①，利用线面平行判定定理和性质定理即可得出四边形ABEF 为平行四边形，又12AB CD =即可得EF 为PCD 的中位线即可得出证明；若选条件②，利用勾股定理可得E 为PC 的中点，再利用线面平行判定定理和性质定理即可得CD EF ∥，即可得出证明；（2）建立以A 为坐标原点的空间直角坐标系，求出平面BCF 的法向量为(2,1,3)m =−，易知AF 是平面PCD 的一个法向量，根据空间向量夹角与二面角之间的关系即可求得结果. 【详解】（1）选条件①：BE AF ∥因为//AB CD ，AB ⊄平面PCD ，CD ⊂平面PCD ， 所以//AB 平面PCD因为平面ABEF ⋂平面PCD EF =， 所以AB EF ∥又//BE AF ， 所以四边形ABEF 为平行四边形． 所以AB EF ∥且AB EF =．因为//AB CD 且12AB CD =，所以//EF CD 且12EF CD =．所以EF 为PCD 的中位线． 所以F 为PD 的中点． 选条件②：BE PC ⊥．因为PA ⊥平面ABCD ，,AB AD ⊂ABCD ，所以,PA AB PA AD ⊥⊥．在Rt PAB 中，PB 在直角梯形ABCD 中，由1AB =，2AD CD ==，可求得BC =PB BC =． 因为BE PC ⊥，所以E 为PC 的中点． 因为ABCD ，AB ⊄平面PCD ，CD ⊂平面PCD ， 所以//AB 平面PCD ．因为平面ABEF ⋂平面PCD EF =，所以AB EF ∥． 所以CD EF ∥， 所以F 为PD 的中点；（2）由题可知因为PA ⊥平面ABCD ，所以,PA AB PA AD ⊥⊥． 又AB AD ⊥，所以,,AB AD AP 两两相互垂直． 如图建立空间直角坐标系A x y z −，则(0,0,0)A ，(1,0,0)B ，(2,2,0)C ，(0,0,2)P ，(0,2,0)D ，(0,1,1)F ．所以(1,2,0)BC =，(,,)111BF =−，(0,1,1)AF =．设平面BCF 的法向量为(,,)m x y z =，则·0·0m BC m BF ⎧=⎪⎨=⎪⎩，即20,0.x y x y z +=⎧⎨−++=⎩ 令1y =−，则2x =，3z =．于是(2,1,3)m =−．因为AB ⊥平面PAD ，且//AB CD ，所以CD ⊥平面PAD ，又AF ⊂平面PAD ，所以AF CD ⊥．又PA AD =，且F 为PD 的中点，所以AF PD ⊥．,,CD PD D CD PD ⋂=⊂平面PCD ，所以AF ⊥平面PCD ，所以AF 是平面PCD 的一个法向量． 7cos ,7m AFm AF m AF ⋅==由题设，二面角B FC P −−的平面角为锐角，所以二面角B FC P −−． 6．(1)证明见解析【分析】(1)根据线面平行的判定定理证明；(2)利用空间向量的坐标运算表示出平面P AC 与平面PCD 的夹角的余弦值，即可求解.【详解】（1）因为底面ABCD 是菱形，所以O 是AC 中点，因为E 是棱P A 的中点，所以//OE PC ，又因为PC ⊂平面PCD , OE ⊄平面PCD ,所以//OE 平面PCD.（2）选择条件①:因为PB PD =，O 是BD 的中点，所以PO BD ⊥,因为平面PBD ⊥平面ABCD ,平面PBD 平面ABCD BD =, PO ⊂平面PBD ，所以PO ⊥平面ABCD ，因为AC ⊂平面ABCD ，所以PO AC ⊥，又AC BD ⊥，所以,,OB OC OP 两两垂直，以O 为原点建立空间直角坐标系O xyz −,因为菱形的边长为2，60BAD ︒∠=所以2,BD AC ==所以(1,0,0),C D −设(0,0,)(0),P t t > 所以(1,3,0),(1,0,)DC DP t ==，设(,,)n x y z =为平面PCD 的一个法向量，由,,n DC n DP ⎧⊥⎪⎨⊥⎪⎩得0,0,n DC n DP ⎧⋅=⎪⎨⋅=⎪⎩所以0,0,x x tz ⎧=⎪⎨+=⎪⎩取,,x y t z ==−=，所以(3,,n t t =−， 因为BO ⊥平面PAC ，所以平面PAC 的一个法向量为1(1,0,0)=n ,平面P AC 与平面PCD 的夹角的余弦值为所以115cos ,5n n <>=所以22543t t =+，所以23t =，因为0t >，所以0t >，所以t =.所以线段OP选择条件②:因为PB AC ⊥.在菱形ABCD 中，BD AC ⊥，因为BD ⊂平面,PBD PB ⊂平面,PBD PBBD B =,所以AC ⊥平面PBD ,因为PO ⊂平面PBD ，所以AC PO ⊥，因为,PO BD AC BD ⊥⊥,所以,,OB OC OP 两两垂直，以O 为原点建立空间直角坐标系O xyz −,因为菱形的边长为2，60BAD ︒∠=所以2,BD AC ==所以(1,0,0),C D −设(0,0,)(0),P t t > 所以(1,3,0),(1,0,)DC DP t ==，设(,,)n x y z =为平面PCD 的一个法向量，由,,n DC n DP ⎧⊥⎪⎨⊥⎪⎩得0,0,n DC n DP ⎧⋅=⎪⎨⋅=⎪⎩所以0,0,x x tz ⎧=⎪⎨+=⎪⎩取,,x y t z ==−=，所以(3,,n t t =−， 因为BO ⊥平面PAC ，所以平面PAC 的一个法向量为1(1,0,0)=n ,平面P AC 与平面PCD所以115cos ,5n n <>=所以22543t t =+，所以23t =，因为0t >，所以0t >，所以t =.所以线段OP7．(1)证明见解析(2)（ⅰ）（ⅱ） 1【分析】（1）利用空间中直线与平面平行的判定定理，结合三角形中位线即可证明；（2）若选条件①，利用1CE B D ⊥，通过推理论证得到1CD B C ==向量，再根据面面夹角的向量公式及点到面的距离公式运算求解；若选条件②，利用1B D 与平面11BCC B 所成角为4π，通过推理论证得到1CD B C ==，建立空间直角坐标系，求平面法向量，再根据面面夹角的向量公式及点到面的距离公式运算求解．【详解】（1）如图，连接1AD ，11B D ，BD .因为长方体1111ABCD A B C D −中,1BB ∥1DD 且11BB DD =，所以四边形11BB D D 为平行四边形.所以E 为1BD 的中点，在1ABD 中，因为E ，F 分别为1BD 和AB 的中点，所以EF ∥1AD .因为EF ⊄平面11ADD A ，1AD ⊂平面11ADD A ，所以EF ∥平面11ADD A .（2）选条件①：1CE B D ⊥.(ⅰ)连接1B C .因为长方体中12AA AD ==，所以1=B C .在1CBD △中,因为E 为1B D 的中点，1CE B D ⊥，所以1CD B C ==如图建立空间直角坐标系D xyz −，因为长方体中12A A AD ==,CD =，则(0,0,0)D ，(2,0,0)A，(0,C，B，F ，1B，E .所以(1,CE =，(2,CF =，(2,0,0)CB =.设平面CEF 的法向量为111(,,)m x y z =，则0,0,m CE m CF ⎧⋅=⎪⎨⋅=⎪⎩即111110,20.x z x ⎧+=⎪⎨=⎪⎩令11x =，则1y =11z =，可得(1,2,1)m =.设平面BCE 的法向量为222(,,)n x y z =，则0,0,n CE n CB ⎧⋅=⎪⎨⋅=⎪⎩即22220,20.x z x ⎧+=⎪⎨=⎪⎩ 令21y =，则20x =，2z =(0,1,2)n =.设平面CEF 与平面BCE 的夹角为θ ， 则||6cos |cos ,|.3||||mn m n m n θ⋅=<>== 所以平面CEF 与平面BCE(ⅱ)因为(0,AF =，所以点A 到平面CEF 的距离为||1||AF m d m ⋅==. 选条件②：1B D 与平面11BCC B 所成角为4π. 连接1B C . 因为长方体1111ABCD A B C D −中，CD ⊥平面11BCC B ，1B C ⊂平面11BCC B ，所以1CD B C ⊥.所以1DB C ∠为直线1B D 与平面11BCC B 所成角，即14DB C π∠=. 所以1DB C 为等腰直角三角形.因为长方体中12AA AD ==，所以1=B C .所以1CD B C ==以下同选条件① .8．(1)证明过程见解析【分析】（1）根据线面垂直的性质，结合相似三角形的判定定理和性质、线面垂直的判定定理进行证明即可；（2）建立空间直角坐标系，利用空间向量夹角公式进行求解即可；（3）利用空间点到直线距离公式进行求解即可.【详解】（1）因为2DC AD ==，M 为BC 的中点，所以AD AB AB AM=， 因为四棱锥P ABCD −的底面是矩形，所以π2DAB MBA ∠=∠=， 所以Rt Rt DAB ABM ∽，所以DBA AMB ∠=∠，而π2MBD DBA ∠+∠=，即π2MBD ANB AM DB ∠+∠=⇒⊥， 因为PD ⊥底面ABCD ，AM ⊂底面ABCD ，所以PD AM ⊥，而,,DBPB B DB PB =⊂平面PBD ，所以AM ⊥平面PBD ；（2）因为PD ⊥平面ABCD ，,AD DC ⊂平面ABCD ，所以,PD AD PD DC ⊥⊥，因为因为四棱锥P ABCD −的底面是矩形，所以AD DC ⊥，建立如下图所示的空间直角坐标系，()()())0,0,0,0,0,2,,2,0D P A M ， 因为PD ⊥平面ABCD ，所以平面ABCD 的法向量为()0,0,2DP =，设平面APM 的法向量为(),,n x y z =，()22PA =−，()2,2,0MA =−，于是有()202,1,220n PA z n n MA y ⎧⎧⊥−=⎪⎪⇒⇒=⎨⎨⊥−=⎪⎪⎩⎩，平面ABCD 与平面APM 所成角的余弦值为(DP n DP n⋅==⋅ （3）由（2）可知平面APM的法向量为()2,1,2n=，4cos ,7DP n 〈〉= 所以D 到平面APM的距离为cos ,2DP DP n ⋅〈〉=9．(1)证明见解析；. 【分析】（1）根据线面垂直的性质得到DE AC ⊥，根据等腰三角形三线合一的性质得到AC BD ⊥，然后利用线面垂直的判定定理证明即可；（2）利用空间向量的方法求线面角即可；（3）利用空间向量的方法求点到面的距离即可.【详解】（1）在三棱柱中，D ，E 为AC ，11A C 的中点，∴1DE AA ∥，∵1AA ⊥平面ABC ，∴DE ⊥平面ABC ，∵AC ⊂平面ABC ，∴DE AC ⊥，在三角形ABC 中，AB BC =，D 为AC 中点，∴AC BD ⊥，∵DE BD D ⋂=，,DE BD 平面BDE ，∴AC ⊥平面BDE .（2）如图，以D 为原点，分别以,,DA DB DE 为,,x y z 轴建立空间直角坐标系，在直角三角形ABD 中，AB =112AD AC ==，∴2BD =， ()0,0,0D ，()0,0,2E ，()1,0,0A ，()0,2,0B ，()0,0,2DE =，()1,2,0AB =−，()1,0,2AE =−，设平面ABE 的法向量为(),,m x y z =，2020AB m x y AE m x z ⎧⋅=−+=⎪⎨⋅=−+=⎪⎩，令2x =，则1y =，1z =，所以()2,1,1m =， 设直线DE 与平面ABE 所成角为θ，所以sin cos ,2DE mDE m DE m θ⋅====⨯⋅（3）设点D 到平面ABE 的距离为d ，所以26DE md m ⋅=== 10．(1)证明见解析(2)π3 【分析】（1）根据条件可以证明//AD 平面PBC ，再利用线面平行的性质定理即可证明出结论；（2）选条件①②可以证明出,,AB AD AP 两两垂直，建立空间直角坐标系A xyz −，求出相应坐标，再求出两平面的法向量，进而求出结果;选条件①③或②③同样可以证明求解.【详解】（1）证明：因为底面ABCD 是正方形，所以//AD BC ，BC ⊂平面PBC ，AD ⊄平面PBC ,所以//AD 平面PBC ，又因为平面ADF 与PB 交于点E .AD ⊂平面ADFE ，平面PBC ⋂平面,ADFE EF = 所以//EF AD .（2）选条件①②侧面PAD 为等腰直角三角形，且π,2PAD ∠=即2PA AD ==，PA AD ⊥平面PAD ⊥平面ABCD ，平面PAD ⋂平面ABCD AD =，PA ⊂平面PAD , 则PA ⊥平面ABCD ，又ABCD 为正方形， 所以,,PA AB PA AD AB AD ⊥⊥⊥.以点A 为坐标原点，,,AB AD AP 分别为x 轴,y 轴,z 轴正方向，建立如图所示空间直角坐标系A xyz −，则(0,0,0),(0,0,2),(2,2,0),(2,0,0),(0,2,0)A P C B D 因为2AE =，所以点E 为PB 的中点，则(1,0,1)E 从而：(2,2,2),(0,2,0),(1,0,1)PC AD AE =−==， 设平面ADFE 的法向量为：(,,)n x y z =， 则020n AE x z n AD y ⎧⋅=+=⎪⎨⋅==⎪⎩， 令1x =，可得(1,0,1)n =−设平面PCD 的法向量为：(,,)n a b c =，则2202220n PD b c n PC a b c ⎧⋅=−=⎪⎨⋅=+−=⎪⎩， 令1b =，可得(0,1,1)n = 所以1cos ,2PB nPB n PB n ⋅== 则两平面所成的锐二面角为π3选条件①③侧面PAD 为等腰直角三角形，且,2PAD π∠=即2,PA AD PA AD ==⊥,AD AB PA AB A ⊥⋂=，且两直线在平面内，可得AD ⊥平面PAB ，PB ⊂平面PAB ，则AD PB ⊥. 又因为,,PB FD AD FD D ⊥⋂=且两直线在平面内， 则PB ⊥平面ADFE ,AE ⊂平面,ADFE 则PB AE ⊥ 因为PA AB =，所以PAB 为等腰三角形，所以点E 为PB 的中点又因为AE PAB 为等腰直角三角形， 下面同①②选条件②③侧面PAD 为等腰直角三角形，且2PAD π∠=，即2,PA AD PA AD ==⊥平面PAD ⊥平面ABCD ，平面PAD ⋂平面ABCD AD =，PA ⊂平面PAD , 则PA ⊥平面,ABCD ABCD 为正方形，所以,,PA AB PA AD AB AD ⊥⊥⊥.又因为,,PB FD AD FD D ⊥⋂=且两直线在平面内，则PB ⊥平面ADFE ，AE ⊂平面,ADFE 则PB AE ⊥因为PA AB =，所以PAB 为等腰三角形，所以点E 为PB 的中点. 下面同①②。

yk iA(x,y,z)O jxzlB'O'A'B O A βα1 空间直角坐标系：（1）若空间的一个基底的三个基向量互相垂直，且长为1，这个基底叫单位正交基底，用{,,}i j k r r r 表示；（2）在空间选定一点O 和一个单位正交基底{,,}i j k r r r ，以点O 为原点，分别以,,i j k r r r 的方向为正方向建立三条数轴：x 轴、y 轴、z 轴，它们都叫坐标轴．我们称建立了一个空间直角坐标系O xyz -，点O叫原点，向量 ,,i j k r r r都叫坐标向量．通过每两个坐标轴的平面叫坐标平面，分别称为xOy 平面，yOz 平面，zOx 平面；2．空间直角坐标系中的坐标： 在空间直角坐标系O xyz -中，对空间任一点A ，存在唯一的有序实数组(,,)x y z ，使OA xi yj zk =++u u u r r r，有序实数组(,,)x y z 叫作向量A 在空间直角坐标系O xyz-中的坐标，记作(,,)A x y z ，x 叫横坐标，y 叫纵坐标，z 叫竖坐标．3．空间向量的直角坐标运算律：（1）若123(,,)a a a a =r ，123(,,)b b b b =r，则112233(,,)a b a b a b a b +=+++r r ，112233(,,)a b a b a b a b -=---r r ，123(,,)()a a a a R λλλλλ=∈r ， 112233a b a b a b a b ⋅=++r r ， 112233//,,()a b a b a b a b R λλλλ⇔===∈r r， 1122330a b a b a b a b ⊥⇔++=r r．（2）若111(,,)A x y z ，222(,,)B x y z ，则212121(,,)AB x x y y z z =---u u u r．一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标4 模长公式：若123(,,)a a a a =r ， 则222123||a a a a a a =⋅=++r r r ．5．夹角公式：112233222222123123cos ||||a ba b a b a a a b b b ⋅⋅==⋅++++r rr r r r ．6．两点间的距离公式：若111(,,)A x y z ，222(,,)B x y z ，则2222212121||()()()AB AB x x y y z z ==-+-+-uuu r uuu r7．直线和平面所成角：（1）定义：平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角 一直线垂直于平面，所成的角是直角一直线平行于平面或在平面内，所成角为0︒角直线和平面所成角范围： [0，2π] （2）定理：斜线和平面所成角是这条斜线和平面内经过斜足的直线所成的一切角中最小的角8．公式：已知平面的斜线a 与内一直线b 相交成θ角，且a 与相交成1角，a 在上的射影c 与b 相交成2角，则有θϕϕcos cos cos 21=ϕ2ϕ1c b aθPαO ABED'B'C'A'ODACBαHDCBA9 二面角的概念：平面内的一条直线把平面分为两个部分，其中的每一部分叫做半平面；从一条直线出发的两个半平面所组成的图形叫做二面角，这条直线叫做二面角的棱，每个半平面叫做二面角的面若棱为l ，两个面分别为,αβ的二面角记为l αβ--10．二面角的平面角：（1）过二面角的棱上的一点O 分别在两个半平面内作棱的两条垂线,OA OB ，则AOB ∠叫做二面角l αβ--的平面角（2）一个平面垂直于二面角l αβ--的棱l ，且与两半平面交线分别为,,OA OB O 为垂足，则AOB ∠也是l αβ--的平面角（1）二面角的平面角范围是[0,180]o o ；（2）二面角的平面角为直角时，则称为直二面角，组成直二面角的两个平面互相垂直11 两个平面垂直的定义：两个相交成直二面角的两个平面互相垂直；相交成直二面角的两个平面叫做互相垂直的平面12．面面垂直的判定定理： 如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直 13．面面垂直的性质定理： 若两个平面互相垂直，那么在一个平面内垂直于它们的交线的直线垂直于另一个平面 练习：1设231(,,)a a a a =r ，231(,,)b b b b =r，且a b ≠r r ，记||a b m -=r r ，求a b -r r 与x 轴正方向的夹角的余弦值2． 在ΔABC 中，已知AB ＝(2,4,0),BC ＝(－1,3,0)，则∠ABC ＝＿＿＿ 3．已知空间三点A(0,2,3),B(－2,1,6),C(1,－1,5)，⑴求以向量AC AB ,为一组邻边的平行四边形的面积S ；⑵若向量a r 分别与向量AC AB ,垂直，且|a r |＝3，求向量a r的坐标4．直角ABC ∆的斜边AB 在平面α内，,AC BC 与α所成角分别为30,45oo，CD 是斜边AB 上的高线，求CD 与平面α所成角的正弦值5．如果二面角l αβ--的平面角是锐角，点P 到,,l αβ的距离分别为22,4,42，求二面角的大小6．如图，正方体的棱长为1，'B C BC O '=I ，求：（1）AO 与A C ''所成角； （2）AO 与平面ABCD 所成角的正切值；（3）平面AOB 与平面AOC 所成角7已知正方体1AC 的棱长为a ，E 是1CC 的中点，O 是对角线1BD 的中点，（1）求证：OE 是异面直线1CC 和1BD 的公垂线；（2）求异面直线1CC 和1BD 的距离参考答案： 1设231(,,)a a a a =r ，231(,,)b b b b =r，且a b ≠r r ，记||a b m -=r r ，αHDCBA求a b -r r与x 轴正方向的夹角的余弦值解：取x 轴正方向的任一向量(,0,0)c x =r，设所求夹角为α，∵22331111()(,,)(,0,0)()a b c a b a b a b x a b x -⋅=---⋅=-r r r∴1111()()cos ||||a b c a b x a bmx m a b c α-⋅--===-⋅r r r r rr ，即为所求 2． 在ΔABC 中，已知AB ＝(2,4,0),BC ＝(－1,3,0)，则∠ABC ＝＿＿＿解：(2,4,0),(1,3,0),BA BC =--=-u u u r u u u rQcos ,||||BA BC BA BC BA BC ⋅∴===u u u r u u u r u u u r u u u r u u u r u u u r ∴∠ABC ＝45°3．已知空间三点A(0,2,3),B(－2,1,6),C(1,－1,5)⑴求以向量,为一组邻边的平行四边形的面积S ；⑵若向量a r 分别与向量AC AB ,垂直，且|a r |＝3，求向量a r的坐标分析：⑴21||||cos ),2,3,1(),3,1,2(==∠∴-=--=AC AB BAC Θ ∴∠BAC ＝60°，3760sin ||||==∴οAC AB S ⑵设a r＝(x,y,z)，则,032=+--⇒⊥z y x AB a33||,023222=++⇒==+-⇒⊥z y x z y x解得x ＝y ＝z ＝1或x ＝y ＝z ＝－1，∴a r ＝(1,1,1)或a r＝(－1，－1，－1).4．直角ABC ∆的斜边AB 在平面α内，,AC BC 与α所成角分别为30,45o o，CD 是斜边AB 上的高线，求CD 与平面α所成角的正弦值解：过点C 作CH α⊥于点H ，连接,,AH BH OH ，则30CAH ∠=o，45CBH ∠=o，CDH ∠为所求CD 与α所成角，记为θ， 令CH a =，则2,AC a BC ==，则在Rt ABC ∆中，有AC BC CD AB ⋅==βαlP C B图1AED'B'C'A'ODACB在Rt CDH ∆中，sin CH CD θ==∴CD 与平面α所成角的正弦值2. 5．如果二面角l αβ--的平面角是锐角，点P 到,,l αβ的距离分别为4,，求二面角的大小分析：点P 可能在二面角l αβ--内部，也可能在外部，应区别处理解：如图1是点P 在二面角l αβ--的内部时，图2是点P 在二面角l αβ--外部时， ∵PA α⊥ ∴PA l ⊥ ∵AC l ⊥ ∴面PAC l ⊥ 同理，面PBC l ⊥而面PAC I 面PBC PC = ∴面PAC 与面PBC 应重合 即,,,A C P B 在同一平面内，则ACB ∠是二面角l αβ--的平面角在Rt APC ∆中，1sin 2PA ACP PB ∠=== ∴30ACP ∠=o在Rt BPC ∆中，sin 2PB BCP PC ∠===∴45BCP ∠=o故304575ACB ∠=+=ooo（图1）或453015ACB ∠=-=ooo（图2） 即二面角l αβ--的大小为75o 或15说明：作一个垂直于棱的平面，此平面与两个半平面的交线所成的角就是二面角的平面角6．如图，正方体的棱长为1，'B C BC O '=I ，求：（1）AO 与A C ''所成角；（2）AO 与平面ABCD 所成角的正切值； （3）平面AOB 与平面AOC 所成角 解：（1）∵//A C AC '' ∴AO 与A C ''所成角就是OAC ∠∵,OC OB AB ⊥⊥平面BC ' ∴OC OA ⊥（三垂线定理）βαlPCB图2AO ED 1C 1B 1A 1DCBA OD 1C 1B 1A 1D CB A在Rt AOC ∆中， 2,2OC AC == ∴30OAC ∠=o （2）作OE BC ⊥，平面BC '⊥平面ABCD∴OE ⊥平面ABCD ，OAE ∠为OA 与平面ABCD 所成角 在Rt OAE ∆中，22115,1()22OE AE ==+= ∴5tan 5OE OAE AE ∠== （3）∵,OC OA OC OB ⊥⊥ ∴OC ⊥平面AOB 又∵OC ⊂平面AOC ∴平面AOB ⊥平面AOC 即平面AOB 与平面AOC 所成角为907已知正方体1AC 的棱长为a ，E 是1CC 的中点，O 是对角线1BD 的中点，（1）求证：OE 是异面直线1CC 和1BD 的公垂线；（2）求异面直线1CC 和1BD 的距离 解：（1）解法一：延长EO 交1A A 于F ，则F 为1A A 的中点，∴//EF AC ， ∵1CC AC ⊥，∴1C C EF ⊥，连结1,D E BE ，则1D E BE =， 又O 是1BD 的中点，∴1OE BD ⊥，∴OE 是异面直线1CC 和1BD 的公垂线（2）由（1）知，OE 122AC ==． 解法二：建立空间直角坐标系，用坐标运算证明（略）引申：求1B C 与BD 间的距离解法一：（转化为1B C 到过BD 且与1B C 平行的平面的距离） 连结1A D ，则1A D //1B C ，∴1B C //平面1A DB ，连1AC ，可证得1AC BD ⊥，1AC AD ⊥，∴1AC ⊥平面1A DB ，∴平面1AC ⊥平面1A DB ，且两平面的交线为1A O ，过C 作1CE AO ⊥，垂足为E ，则CE 即为1B C 与平面1A DB 的距离，也即1B C 与BD 间的距离，在1A OC ∆中，111122OC A A CE AO ⋅=⋅，∴CE a =． （解法二）：坐标法：以D 为原点，1,,DA DC DD 所在的直线分别为x 轴，y 轴、z 轴建立空间直角坐标系， 则(,0,0),(,,0),(0,,0)A a B a a C a ，11(,,),(,0,),(0,0,0)B a a a A a a D ， 由（解法一）求点C 到平面1A DB 的距离CE ，设(,,)E x y z ， ∵E 在平面1A DB 上，∴111A E A D A B λμ=+u u u u r u u u u r u u u r，即(,,)(,0,)(0,,)x a y z a a a a a λμ--=--+，∴x a a y a z a a a λμμλ=-⎧⎪=⎨⎪=--⎩， ∵1,CE A D CE BD ⊥⊥u u u r u u u u r u u u r u u u r ，∴(,2,)(,0,)0(,2,)(,,0)0x y z a a x y z a a ---=⎧⎨---=⎩，解得：23λμ==，∴111(,,)333CE a a a =--u u u r，∴3CE a =． 解法三：直接求1B C 与BD 间的距离设1B C 与BD 的公垂线为1OO ，且11,O B C O BD ∈∈，设(,,)O x y z ，设DO BD λ=u u u r u u u r，则(,,)(,,0)x y z a a λ=--，∴0x a y a z λλ=-⎧⎪=-⎨⎪=⎩，∴(,,0)O a a λλ--，同理1(,,)O a a a μμ，∴1((),,)OO a a a a μλλμ=++u u u u r ，∴111,OO BD OO B C ⊥⊥u u u u r u u u r u u u u r u u u u r ， ∴1110,0OO BD OO B C ⋅=⋅=u u u u r u u u r u u u u r u u u u r，解得：21,33λμ=-=，1OO =u u u u r 111(,,)333a a a -，1||OO =u u u u r ．。

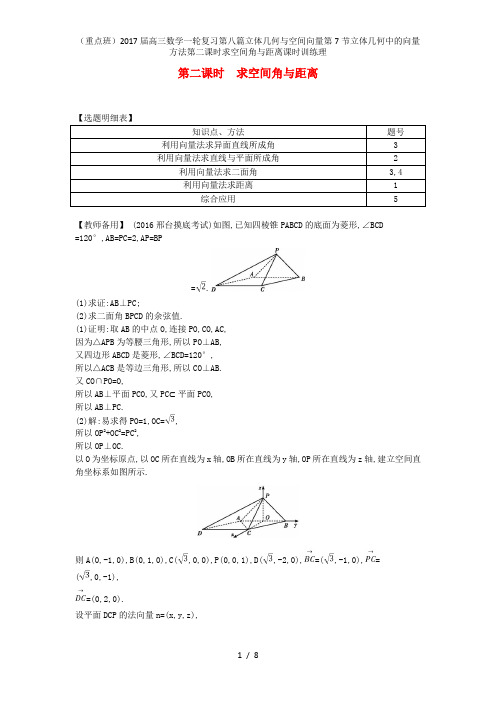
第二课时求空间角与距离知识点、方法题号利用向量法求异面直线所成角 3利用向量法求直线与平面所成角 2利用向量法求二面角3,4利用向量法求距离 1综合应用 5【教师备用】 (2016邢台摸底考试)如图,已知四棱锥PABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=.(1)求证:AB⊥PC;(2)求二面角BPCD的余弦值.(1)证明:取AB的中点O,连接PO,CO,AC,因为△APB为等腰三角形,所以PO⊥AB,又四边形ABCD是菱形,∠BCD=120°,所以△ACB是等边三角形,所以CO⊥AB.又CO∩PO=O,所以AB⊥平面PCO,又PC⊂平面PCO,所以AB⊥PC.(2)解:易求得PO=1,OC=,所以OP2+OC2=PC2,所以OP⊥OC.以O为坐标原点,以OC所在直线为x轴,OB所在直线为y轴,OP所在直线为z轴,建立空间直角坐标系如图所示.则A(0,-1,0),B(0,1,0),C(,0,0),P(0,0,1),D(,-2,0),=(,-1,0),=(,0,-1),=(0,2,0).设平面DCP的法向量n=(x,y,z),则即令x=1,得所以n=(1,0,),设平面PCB的法向量m=(a,b,c),即令a=1,则b=c=,所以m=(1,,),所以cos<m,n>==,由图易知二面角BPCD的平面角为钝角.所以二面角BPCD的余弦值为-.1.(2016郑州第一次质量预测)如图,在四棱锥PABCD中,底面ABCD为直角梯形,AD∥BC,PD⊥底面ABCD,∠ADC=90°,AD=2BC,Q为AD的中点,M为棱PC的中点.(1)证明PA∥平面BMQ;(2)已知PD=DC=AD=2,求点P到平面BMQ的距离.(1)证明:连接AC交BQ于N,连接MN,因为∠ADC=90°,Q为AD的中点,所以N为AC的中点,又M为PC的中点,MN为△PAC的中位线,故MN∥PA,又MN⊂平面BMQ,所以PA∥平面BMQ.(2)解:以D为坐标原点,DA,DC,DP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,D(0,0,0),A(2,0,0),C(0,2,0),P(0,0,2),Q(1,0,0),B(1,2,0),M(0,1,1).所以=(0,-1,1),=(-1,1,1),=(-1,-1,1),设n=(x,y,z)是平面BQM的法向量,则n⊥,n⊥,所以即令z=1,则x=1,y=0,所以n=(1,0,1),则P点到平面BQM的距离为d===.2.(2015高考新课标全国卷Ⅱ)如图,长方体ABCDA1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由);(2)求直线AF与平面α所成角的正弦值.解:(1)交线围成的正方形EHGF如图.(2)作EM⊥AB,垂足为M,则AM=A1E=4,EM=AA1=8.因为EHGF为正方形,所以EH=EF=BC=10.于是MH==6,所以AH=10.以D为坐标原点,的方向为x轴正方向,建立如图所示的空间直角坐标系Dxyz,则A(10,0,0),H(10,10,0), E(10,4,8),F(0,4,8),=(10,0,0),=(0,-6,8).设n=(x,y,z)是平面EHGF的法向量,则即所以可取n=(0,4,3).又=(-10,4,8),故|cos<n,>|==.所以AF与平面α所成角的正弦值为.3.(2016贵阳监测考试)如图,已知四棱锥PABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AB⊥AC,AB=AC=PA=2,E是BC的中点.(1)求异面直线AE与PC所成的角;(2)求二面角DPCA的平面角的余弦值.解:(1)如图所示,以A点为原点建立空间直角坐标系Axyz,则B(2,0,0),C(0,2,0),P(0,0,2).故E(1,1,0),=(1,1,0),=(0,2,-2),cos<,>==,即<,>=60°,故异面直线AE与PC所成的角为60°.(2)因为AB=AC=2,AB⊥AC,所以∠ABC=∠ACB=45°,因为AD∥BC,所以∠DAC=∠ACB=45°,又AD⊥CD,所以AD=CD=,所以D(-1,1,0),又C(0,2,0),所以=(-1,-1,0),=(0,2,-2).设n=(x,y,z)是平面PCD的法向量,则⊥n,⊥n,即·n=0,·n=0,所以令x=-1得y=1,z=1,则n=(-1,1,1),|n|=.又AB⊥平面PAC,所以=(2,0,0)是平面PAC的一个法向量,所以cos<,n>==-,所以二面角DPCA的平面角的余弦值为.4.(2015河南三市第三次调研)在三棱锥PABC中,PA⊥底面ABC,PB=PC=, BC=4,PA=m(m>0).(1)当m为何值时,点A到平面PBC的距离最大,并求出最大值;(2)当点A到平面PBC的距离取得最大值时, 求二面角APBC的余弦值.解:(1)设D为BC的中点,连接AD,PD,因为PA⊥平面ABC,所以PA⊥BC.在等腰三角形PBC中,因为BD=DC,所以BC⊥PD,又因为PD∩PA=P,所以BC⊥平面PAD,又因为BC⊂平面PBC,所以平面PBC⊥平面PAD.在平面PAD中,过A作AM⊥PD于M,则AM⊥平面PBC.即AM为点A到平面PBC的距离.在△PDB中,PD==3.在Rt△PAD中,AD==,且PA·AD=PD·AM,所以AM===≤,当且仅当m2=18-m2,即m=3时等号成立.故当m=3时,点A到平面PBC的距离最大,最大值为.(2)当m=3时,AD=3,过D作DE∥AP,以点D为坐标原点,分别以DA,DB,DE所在直线为x,y,z 轴,建立空间直角坐标系如图所示.则A(3,0,0),P(3,0,3),B(0,2,0),C(0,-2,0),所以=(0,0,3),=(3,-2,3),=(0,4,0).设平面PAB的法向量p=(x,y,z).则即即取p=(,1,0).同理,平面PBC的一个法向量q=(1,0,-1).cos<p,q>==.所以二面角APBC的余弦值为.5. 如图,侧棱垂直于底面的三棱柱ABCA1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.(1)当AA1=AB=AC时,求证:A1C⊥平面ABC1;(2)试求三棱锥PBCC1的体积V取得最大值时的t值;(3)若二面角ABC1C的平面角的余弦值为,试求实数t的值.(1)证明:因为AA1⊥平面ABC,AB,AC⊂平面ABC,所以AA1⊥AC,AA1⊥AB.又AB⊥AC,所以以A为原点,分别以AB,AC,AA1所在直线为x轴,y轴,z轴建立如图所示的空间直角坐标系.则A(0,0,0),C1(0,1,1),B(1,0,0),C(0,1,0),A1(0,0,1),=(0,1,-1),=(0,1,1),=(1,0,0).设平面ABC1的法向量n=(x,y,z),则解得令z=1,则n=(0,-1,1).因为=-n,所以A1C⊥平面ABC1.(2)解:因为AA1∥平面BB1C1C,所以点P到平面BB1C1C的距离等于点A到平面BB1C1C的距离.所以V===t2(3-2t)=t2-t3(0<t<),令f(t)=t2-t3,则f′(t)=-t(t-1),易得f(t)在(0,1)递增,在(1, )递减,所以当t=1时,V max=.(3)解:A(0,0,0),C1(0,t,3-2t),B(t,0, 0),C(0,t,0),A1(0,0,3-2t),=(0,t,2t-3),=(0,t,3-2t),=(t,0,0),=(0,0,3-2t),=(-t,t,0).设平面ABC1的法向量为n1=(x1,y1,z1),则解得令z1=t,则n1=(0,2t-3,t).设平面BCC1的法向量为n2=(x2,y2,z2),则解得令y2=1,则n2=(1,1,0).设二面角ABC1C的平面角为θ,则有cos θ===.化简得5t2-16t+12=0,解得t=2(舍去)或t=.所以当t=时,二面角ABC1C的平面角的余弦值为.。

专题立体几何与空间向量作者：朱振华来源：《高考进行时·高三数学》2012年第12期（1）当BD的长为多少时，三棱锥的ABCD体积最大；（2）当三棱锥ABCD的体积最大时，设点E，M分别为棱BC，AC的中点，试在棱CD 上确定一点N，使得EN⊥BM，并求EN与平面BMN所成角的大小.图1图2（作者：卢杰江苏省丹阳高级中学）立体几何在高考中占有重要的地位，近几年对立体几何考查的重点与难点趋于稳定（也是考生的基本得分点）：高考始终把直线与直线、直线与平面、平面与平面的平行的判断与性质、垂直的判断与性质作为考查的重点。

新课标教材对立体几何要求虽有所降低，但考查的重点一直没有变，常常考查线线、线面、面面的平行与垂直的位置关系和选修中的空间角与距离的计算。

在现有的必修教材中，虽淡化了利用空间关系找角、找距离这方面的讲解，但在理科选修教材中加大了向量的应用。

学习空间向量后，立体几何问题大多可以用向量的知识来做，从而使解题更简捷有效。

对空间向量的考查主要集中于向量概念与运算，要涉及空间向量的坐标及运算、空间向量的应用，尤其是求夹角、求距离。

一、考纲要求1. 空间几何体：该部分要牢牢抓住各种空间几何体的结构特征，通过对各种空间几何体结构特征的了解，认识各种空间几何体直观图，在此基础上掌握好空间几何体的表面积和体积的计算方法；2. 空间点、直线、平面的位置关系：该部分的基础是平面的性质、空间直线与直线的位置关系，重点是空间线面平行和垂直关系的判定和性质，面面平行和垂直关系的判定和性质.在复习中要牢牢掌握四个公理和八个定理及其应用，重点掌握好平行关系和垂直关系的证明方法；3. 空间向量与立体几何：由于有平面向量的基础，空间向量部分重点掌握好空间向量基本定理和共面向量定理，在此基础上把复习的重心放在如何把立体几何问题转化为空间向量问题的方法，并注重运算能力的训练。

二、难点疑点1. 空间几何体的表面积和体积的计算方法；2. 平行关系和垂直关系的判定和性质，掌握好平行和垂直关系的证明方法；3. 空间向量的应用，将立体几何问题转化为空间向量问题的方法。

双曲线1．双曲线的定义平面内与两个定点1F ，2F 的距离的差的绝对值是常数（大于零且小于12||F F ）的点的轨迹叫双曲线．这两个定点叫做双曲线的焦点，两焦点的距离叫焦距．12{|||2}M MF |MF a -=1202||a F F <<（）2．双曲线的标准方程（1）当焦点在x 轴上时，双曲线的标准方程：2222100x y a b ab-=>>（，），（2）当焦点在y 轴上时，双曲线的标准方程：2222100y x a b a b-=>>（，），其中222c a b =+． 3．双曲线22221x y a b -=与2222100y x a b a b-=>>（，）的简单几何性质4．弦长公式：若直线y kx b =+与双曲线相交于两点A 、B ，且12x x ，分别为A ，B的横坐标，则AB =，12AB x =-．若12y y ，分别为A ，B 的纵坐标，则12AB y -=．考点一 双曲线定义例1．到两定点1(30)F -，、2(30)F ，的距离之差的绝对值等于6的点M 的轨迹（ ）A ．椭圆B ．线段C ．双曲线D ．两条射线例2．已知两点12(50)(50)F F -，，，，求与它们的距离差的绝对值等于6的动点的轨迹方程 ． 例3．双曲线221169x y -=上的点P 到点(5，0)的距离为15，则P 到点(-5，0)的距离是（ ）A ．7B ．23C ．25或7D ．7或23例4．过双曲线221169xy -=左焦点F 1的弦AB 长为6，则2ABF △（2F 为右焦点）的周长是（ ）A ．28B ．22C ．14D ．12例5．椭圆22162xy +=和双曲线2213x y -=的公共焦点为12F F P ，，是两曲线的一个交点， 那么12cos F PF ∠的值是_____________．考点二 标准方程例6．曲线22832x y -=的焦点坐标为 ，虚轴长为 ． 例7．双曲线22221124x y m m -=+-的焦距是（） A ．4 B ．22C ．8D ．与m 有关例8．已知椭圆22219x y a +=（a > 0）与双曲线22143x y -=有相同的焦点，则a 的值为（ ）A B ． C ．4D ．10例9．已知方程22111x y k k-=+-表示双曲线，则k 的取值范围是（ ） A ．11k -<<B ．k > 1C ．k ≥0D ．k > 1或k < -1例10．θ是第三象限角，方程22sin cos x y θθ+=表示的曲线是（ ）A ．焦点在x 轴上的椭圆B ．焦点在y 轴上的椭圆C ．焦点在x 轴上的双曲线D ．焦点在y 轴上的双曲线例11．已知圆C ：x 2 + y 2 - 6x - 4y + 8 = 0．以圆C 与坐标轴的交点分别作为双曲线的一个焦点和顶点，则适合上述条件的双曲线的标准方程为________．考点三 渐近线例12．双曲线3x 2 - y 2 = 3的渐近线方程是（ ）A ．y =3x ±B ．y =13x ±C ．y =D ．y =例13．中心在原点，焦点在x 轴上的双曲线的实轴与虚轴相等，一个________． 例14．与双曲线221916x y -=有共同的渐近线，且经过点(3A -，的双曲线的一个焦点到一条渐近线的距离是（ ） A ．8 B ．4 C ．2D ．1例15．已知直线y = kx + 2与双曲线x 2 - y 2 = 6的右支交于不同的两点，则k 的取值范围是（ ）A ．⎛⎝⎭B ．03⎛⎝⎭，C ．1⎛⎫- ⎪⎝⎭D ．0⎛⎫ ⎪⎝⎭例16．若直线1y kx =+与曲线x 有两个不同的交点，则k 的取值范围是（ ）A ．k <B ．1k <<-C ．1k <D ．k <k >考点四 离心率例17．，焦距为6，则双曲线离心率是（ ）AB C ．32D ．23例18．已知双曲线22212x ya a-=>（的两条渐近线的夹角为3π，则双曲线的离心率为（ ）A BC ．D ．2例19．中心在原点，焦点在x 轴上的双曲线的一条渐近线经过点(4，-2)，则它的离心率为（ ）A BC ．D 例20．设双曲线2222100x y a b a b-=>>（，）的实轴长，虚轴长，焦距依次成等差数列，那么这个双曲线的离心率e 等于（ ）A ．2B ．3C ．53D ．43例21．已知F 1，F 2是双曲线2222100x y a b a b-=>>（，）的两焦点，以线段F 1F 2为边作正△MF 1F 2，若边MF 1的中点在双曲线上，则双曲线的离心率是（ ）A ．4+B 1CD 1例22．设F 1，F 2分别是双曲线22221x y a b-=的左，右焦点．若双曲线上存在点A ，使∠F 1AF 2 = 90°，且|AF 1| = 3|AF 2|，则双曲线离心率为（ ）A BC ．D 例23．双曲线2222100x y a b ab-=>>（，）的左、右焦点分别是F 1，F 2，过F 1作倾斜角为30°的直线交双曲线右支于M 点，若MF 2垂直于x 轴，则双曲线的离心率为（ ）A ．B ．CD考点五 焦点三角形例24．设P 为双曲线22112yx -=上的一点，F 1，F 2是该双曲线的两个焦点，若12||||32PF PF =::，则12PF F △的面积为（ ）A ．B ．12C ．D ．24例25．已知双曲线的左、右焦点分别为F 1，F 2，在左支上过F 1的弦AB 的长为5，若2a = 8，那么△ABF 2的周长是（ ） A ．16 B ．18 C ．21D ．26例26．设F 1和F 2为双曲线221169x y -=的两个焦点，点P 在双曲线上且满足1290F PF ∠=︒，求12F PF △的面积．例27．已知双曲线的方程是16x 2 - 9y 2 = 144．（1）求此双曲线的焦点坐标、离心率和渐近线方程；（2）设F 1、F 2是双曲线的左、右焦点，点P 在双曲线上，12||||32PF PF ⋅=，求∠F 1PF 2．。

椭圆1．椭圆的第一定义平面内一个动点P 到两个定点1F 、2F 的距离之和等于常数（1212||||2||PF PF a F F +=>），这个动点P 的轨迹叫椭圆．这两个定点叫椭圆的焦点，两焦点的距离叫做椭圆的焦距．注：若1212||||||PF PF F F +=，则动点P 的轨迹为线段12F F ；若12||||PF PF +<12||F F ，则动点P 的轨迹无图形．2．椭圆的标准方程（1）当焦点在x 轴上时，椭圆的标准方程：222210x y a b ab+=>>（），其中222c a b =-；（2）当焦点在y轴上时，椭圆的标准方程：222210y x a b a b+=>>（），其中222c a b =-．3．椭圆22221x y+=与22221y x +=0a b >>（）的简单几何性质4．离心率（1）椭圆的焦距与长轴长度的比叫做椭圆的离心率，用e表示，记作2 2c cea a==；（2）因为0a c>>，所以e的取值范围是01e<<．e越接近1，则c就越接近a，从而b=越小，因此椭圆越扁；反之，e越接近于0，c就越接近0，从而b越接近于a，这时椭圆就越接近于圆．当且仅当a b=时，0c=，这时两个焦点重合，图形变为圆，方程为222x y a+=．例1．判断下面结论是否正确．（请在括号中打“√”或“×”）（1）平面内与两个定点F1，F2的距离之和等于常数的点的轨迹是椭圆．（）（2）椭圆上一点P与两焦点F1，F2构成△PF1F2的周长为2a + 2c（其中a为椭圆的长半轴长，c为椭圆的半焦距）（）（3）方程mx2 + ny2 = 1（m > 0，n > 0，m n≠）表示的曲线是椭圆．（）例2．如图所示，A是圆O内一定点，B是圆周上一个动点，AB的中垂线CD与OB 交于E ，则点E 的轨迹是（ ）（例2）A ．圆B ．椭圆C ．双曲线D ．抛物线考点二 椭圆的基本量及标准方程例3．已知椭圆221102x y m m +=--的焦距为4，则m 等于（ ） A ．4 B ．8 C ．4或8D ．以上均不对 例4．设椭圆的标准方程为22135x y k k+=--，若其焦点在x 轴上，则k 的取值范围是（ ）A ．k > 3B ．3 < k < 5C ．4 < k < 5D ．3 < k < 4例5．设A ，B 是椭圆C ：2213x y m+=长轴的两个端点，若C 上存在点M 满足∠AMB = 120°，则m 的取值范围是（ ）A ．(0，1][9，+∞)B ．(0，3][9，+∞)C ．(0，1][4，+∞)D ．(03][4，+∞) 例6．一个圆经过椭圆221164x y +=的三个顶点，且圆心在x 轴上，则该圆的标准方程为_______．例7．已知椭圆C ：222210x ya b ab+=>>（），四点P 1(1，1)，P 2(0，1)，331P ⎛- ⎝⎭，，4312P ⎛ ⎝⎭，中恰有三点在椭圆C 上．求C 的方程 ．例8．若椭圆22221x y ab +=的焦点在x 轴上，过点(2，1)作圆x 2 + y 2 = 4的切线，切点分别为A ，B ，直线AB 恰好经过椭圆的右焦点和上顶点，则椭圆方程为 ． 例9．已知椭圆E ：222210x y a b ab+=>>（）的右焦点为(30)F ，，过点F 且斜率为12的直线交椭圆E 于A 、B 两点．若AB 的中点坐标为(11)-，，则E 的方程为（ ） A ．2214536xy += B ．2213627xy +=C ．2212718x y +=D ．221189x y +=考点三 椭圆的离心率例10．已知椭圆222210x y a b ab+=>>（）： （1）若长轴长、短轴长、焦距为等差数列，则该椭圆的离心率为 ；（2）若长轴长、短轴长、焦距为等比数列，则该椭圆的离心率为 ． 例11．椭圆22194x y +=的离心率是（ ）A ．B C ．23D ．59例12．直线l 经过椭圆的一个顶点和一个焦点，若椭圆中心到l 的距离为其短轴长的14，则该椭圆的离心率为（ ） A ．13B ．12C ．23D ．34例13．已知椭圆C ：222210x y a b a b+=>>（）的左、右顶点分别为A 1，A 2，且以线段A 1A 2为直径的圆与直线bx - ay + 2ab = 0相切，则C 的离心率为（ ）A ．BCD ．13例14．椭圆上一点A 看两焦点的视角为直角，设AF 1的延长线交椭圆于B ，又2||||AB AF =，则椭圆的离心率e =（ ）A．2-+ BC1 D例15．如图所示，“嫦娥一号”探月卫星沿地月转移轨道飞向月球，在月球附近一点P 变轨进入以月球球心F 为一个焦点的椭圆轨道Ⅰ绕月飞行，之后卫星在P 点第二次变轨进入仍以F 为一个焦点的椭圆轨道Ⅱ绕月飞行，最终卫星在P 点第三次变轨进入以F 为圆心的圆形轨道Ⅲ绕月飞行，若用2c 1和2c 2分别表示椭轨道Ⅰ和Ⅱ的焦距，用2a 1和2a 2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长，给出下列式子：①a 1+ c 1= a 2+ c 2；②a 1 - c 1= a 2 - c 2；③a 2c 1> a 1c 2；④1212c c a a <．其中正确式子的序号是（ ）（例15）B ．②③C ．①④D ．②④例16．已知椭圆方程为221499xy +=中，12F F ，分别为它的两个焦点，则下列说法正确的有（ ）①焦点在x 轴上，其坐标为(70)±，；②若椭圆上有一点P 到1F 的距离为10，则P 到2F 的距离为4； ③焦点在y 轴上，其坐标为(0±，； ④a = 49，b = 9，c = 40． A ．0个 B ．1个 C ．2个D ．3个例17．点M 是椭圆2212516xy +=上一点，它到其中一个焦点F 1的距离为2，N 为MF 1的中点，O 表示原点，则||ON =（ ）A ．32B ．2C ．4D ．8例18．已知P 为椭圆221259xy +=上动点，F 为椭圆的右焦点，点A 的坐标为(3，1)，则||PF +||PA 的最小值为（ ） A ．102+ B ．102- C ．1052+D ．1052-例19．椭圆有这样的光学性质：从椭圆的一个焦点出发的光线，经椭圆反射后，反射光线经过椭圆的另一个焦点，今有一个水平放置的椭圆形台球盘，点A 、B 是它的焦点，长轴长为2a ，焦距为2c ，静放在点A 的小球（小球的半径不计），从点A 沿直线出发，经椭圆壁反弹后第一次回到点A 时，小球经过的路程是（ ） A ．4aB ．2(a - c )C ．2(a + c )D ．以上答案均有可能 例20．求过椭圆22142xy +=的一个焦点F 1的弦AB 与另一个焦点F 2围成的三角形△ABF 2的周长是_______． 例21．过原点O 作两条相互垂直的直线分别与椭圆P ：2212x y +=交于A 、C 与B 、D ，则四边形ABCD 面积的最小值为（ ） A ．83B ．2C ．2D ．43例22．已知P 是椭圆22110036x y +=上一点，F 1、F 2分别是椭圆的左、右焦点，若∠F 1PF 2 = 60°，则△PF 1F 2的面积为________．例23．已知椭圆22195x y +=的右焦点为F ，P 是椭圆上一点，点A (0，3)，当△APF 的周长最大时，△APF 的面积等于________．例24．设12F F ，分别是椭圆22221x y a b +=（0a b >>）的左、右焦点，若在直线2a l x c=：上存在P（其中c =），使线段1PF 的中线过点2F ，则椭圆离心率的取值范围是（ ）A ．02⎛⎝⎦，B ．03⎛⎝⎦，C．12⎫⎪⎢⎣⎭D．1⎫⎪⎣⎭例25．如图，设椭圆的中心为原点O ，长轴在x 轴上，上顶点为A ，左、右焦点分别为F 1，F 2，线段OF 1，OF 2的中点分别为B 1，B 2，且△AB 1B 2是面积为4的直角三角形．（例25）（2）过B 1作直线l 交椭圆于P ，Q 两点，使PB 2⊥QB 2，求直线l 的方程。

直线与园考点一 圆的方程例1．圆心为(3，4)，且经过坐标原点的圆的方程是（ ）A ．22(3)(4)25x y -+-=B ．22(3)(4)5x y -+-=C ．22(3)(4)25x y +++=D ．22(3)(4)5x y +++=例2．若圆C 的半径为1，其圆心与点(1，0)关于直线y x =对称，则圆C 的标准方程为_______．例3．若关于x ，y 的方程22240x y x y m +--+=表示圆，则实数m 的取值范围是 ．例4．过点(52)(32)，，，M N 且圆心在直线23y x =-上的圆的方程为 ．考点二 直线与圆的位置关系例5．将直线20x y λ-+=，沿x 轴向左平移1个单位，所得直线与圆22240x y x y ++-=相切，则实数λ的值为（） A ．-3或7 B ．-2或8 B ．0或10D ．1或11例6．圆2240x y x +-=在点(1P 处的切线方程为（ ）A ．20x -=B ．40x -=C ．40x +=D ．20x +=例7．过点(22)，P 的直线与圆22(1)5x y -+=相切，与直线10ax y -+=垂直，则a = ．例8．若经过点(10)，P -的直线与圆224230x y x y ++-+=相切，则此直线在y 轴上的截距是 ．例9．圆C ：222440x y x y +--+=的圆心到直线3440x y ++=的距离d =_______． 例10．若直线2x my m +=+与圆222210x y x y +--+=相交，则实数m 的取值范围是（ ）A ．()，-∞+∞B ．(0)，-∞C ．(0)，+∞D ．(0)(0)，，-∞+∞例11．若直线10x y -+=与圆22()2x a y -+=有公共点，则实数a 的取值范围是（ ）A ．[31]，--B ．[13]，-C ．[31]，-D ．(3][1)，，-∞-+∞例12．圆222440x y x y +-+-=与直线2220（）tx y t t ---=∈R 的位置关系为（ ） A ．相交 B ．相切 C ．相离D ．相交或相切例13．已知点()，M a b 在圆221：O x y +=外，则直线1ax by +=与圆O 的位置关系是 ．例14．直线l 过点(20)，-，l 与圆222x y x +=有两个交点时，斜率k 的取值范围是（ ）A ．(-B ．(C ．⎛⎝⎭D ．1188，⎛⎫- ⎪⎝⎭例15．若过定点(10)，M -且斜率为k 的直线与圆22450x x y ++-=在第一象限内的部分有交点，则k 的取值范围是（ ） A ．0k <<B ．0k <C ．0k <<D ．05k <<例16．若直线y x m =+与曲线y =m 的取值范围．例17．圆22(3)(3)9x y -+-=上到直线34110x y +-=的距离为1的点有几个？例18．圆222430x y x y +++-=上到直线10x y ++= ）A ．1个B ．2个C ．3个D ．4个例19．设直线3y ax =+与圆222410x y x y +--+=相交于，A B 两点，且||AB =，则a =_______．例20．0y +-=截圆224x y +=得的劣弧所对的圆心角为（ ）A ．30°B ．45°C ．60°D ．90°例21．如果一条直线经过点332，M ⎛⎫-- ⎪⎝⎭，且被圆2225x y +=截得的弦长等于8，那么这条直线的方程为（ ）A ．3x =-B ．332或x y =-=- C ．34150x y ++= D ．334150或x x y =-++=例22．直线L 将圆22240x y x y +--=平分，且与直线20x y +=垂直，则直线L 的方程为（ ）A ．2y x =B ．22y x =-C ．1322y x =-+D ．1322y x =+例23．已知(30)，M 是圆2282100x y x y +--+=内一点，过M 点最长的弦所在的直线方程是（ ）A ．30x y +-=B ．30x y --=C ．260x y --=D ．260x y +-=例24．若点(11)，P 为圆22(3)9x y -+=的弦MN 的中点，则弦MN 所在直线的方程为 ．例25．圆222210x y x y +--+=上的点到直线2x y -=的距离最大值是（ ）A ．2B ．1C ．1+D ．1+例26．P 为圆221x y +=上的动点，则点P 到直线34100x y --=的距离的最小值为_______．例27．过点M (1，2)的直线l 将圆22(2)9x y -+=分成两段弧，当其中的劣弧最短时，直线的方程是（ ）A ．1x =B ．1y =C ．10x y -+=D ．230x y -+=考点三 圆与圆的位置关系例28．圆22(2)4x y ++=与圆22(2)(1)9x y -+-=的位置关系是__________． 例29．圆2220x y x +-=和圆2240x y y ++=的公切线共有________条．例30．圆22126260：C x y x y ++--=与圆2224240：C x y x y +-++=的位置关系是__________．例31．对于任意实数k ，直线(32)20k x ky +--=与圆222220x y x y +---=的位置关系是_____．例32．若圆222240x y mx m +-+-=与圆22224480x y x my m ++-+-=相切，则实数m的取值集合是_____________．例33．两圆2210x y +=和22(1)(3)20x y -+-=相交于A ，B 两点，则直线AB 方程为 ．例34．若圆224x y +=与圆222600（）x y ay a ++-=>的公共弦长为则a = ．考点四 求切线例35．过点(21)-,作圆225x y +=的切线，其方程是（ ）A ．240x y --=B ．250x y --=C ．230x y +-=D ．250x y --=或240x y -+=例36．平行于直线210x y ++=且与圆225x y +=相切的直线的方程是（ ）A ．250x y ++=或250x y +-=B ．20x y +=或20x y +=C ．250x y -+=或250x y --=D ．20x y -=或20x y -=例37．直角坐标平面内，过点P (21),且与圆224x y +=相切的直线（ ）A ．有两条B ．有且仅有一条C ．不存在D ．不能确定例38．由圆221x y +=外一点P (21),引圆的切线，切线长为（ ）A ．B ．2C ．1D ．4例39．由直线2y x =+上的点向圆22(2)(2)1x y -++=引切线，则切线长的最小值为（ ）A ．B ．4C ．D 例40．在平面直角坐标系xOy 中，以点（1，0）为圆心且与直线mx ﹣y ﹣2m ﹣1=0（m ∈R ）相切的所有圆中，半径最大的圆的标准方程为： 。