1.2 特殊角的三角函数
- 格式:docx
- 大小:76.40 KB
- 文档页数:2


北师大版九年级数学下册:1.2《30度,45度,60度角的三角函数值》教学设计一. 教材分析《30度,45度,60度角的三角函数值》是北师大版九年级数学下册第一章第二节的内容。
本节课主要让学生掌握30度,45度,60度角的正弦、余弦、正切函数值,并会运用这些特殊角的三角函数值解决实际问题。
这一内容是学生进一步学习三角函数的基础,对于培养学生的数学思维能力和解决问题的能力具有重要意义。
二. 学情分析九年级的学生已经学习了锐角三角函数的概念,对正弦、余弦、正切函数有一定的了解。
但学生对于特殊角的三角函数值的认识还比较模糊,需要通过实例和练习来加深理解。
此外,学生对于解决实际问题的能力有待提高,需要教师在教学中进行引导和培养。
三. 教学目标1.知识与技能目标:让学生掌握30度,45度,60度角的正弦、余弦、正切函数值,并能运用这些值解决实际问题。
2.过程与方法目标:通过观察、实验、探究等方法,让学生体验特殊角的三角函数值的求解过程,培养学生的数学思维能力和解决问题的能力。
3.情感态度与价值观目标:让学生在解决实际问题的过程中,体验数学与生活的紧密联系,增强学习数学的兴趣和自信心。
四. 教学重难点1.重点:掌握30度,45度,60度角的正弦、余弦、正切函数值。
2.难点:运用特殊角的三角函数值解决实际问题。
五. 教学方法1.引导发现法:教师通过提问、引导,激发学生的思考,让学生主动发现和总结特殊角的三角函数值。
2.情境教学法:教师创设生活情境,让学生在实际问题中运用特殊角的三角函数值,培养学生的解决问题的能力。
3.小组合作学习:教师学生进行小组讨论和合作,让学生在互动中学习,提高学习效果。
六. 教学准备1.教具:三角板、直尺、多媒体设备等。
2.学具:学生每人准备一份特殊角的三角函数值表格。
七. 教学过程1.导入(5分钟)教师通过提问:“你们已经掌握了哪些锐角三角函数值?”引导学生回顾已学的知识,为新课的学习做好铺垫。



北师大版数学九年级下册1.2《特殊的三角函数值》说课稿一. 教材分析北师大版数学九年级下册1.2《特殊的三角函数值》这一节的内容,主要介绍了特殊角的三角函数值。
这部分内容是初中数学中三角函数知识的重要组成部分,也是学生进一步学习高中数学的基础。
在教材中,通过介绍特殊角的三角函数值,让学生掌握锐角三角函数的定义和计算方法,并能够运用这些知识解决实际问题。
二. 学情分析九年级的学生已经学习了初中数学的前置知识,对函数的概念和性质有一定的了解。
但是,对于三角函数的定义和计算方法,可能还存在一定的困难。
因此,在教学过程中,需要引导学生通过观察、思考、探究,从而理解并掌握特殊角的三角函数值。
三. 说教学目标1.知识与技能:让学生掌握特殊角的三角函数值,能够运用这些知识解决实际问题。
2.过程与方法:通过观察、思考、探究,培养学生的逻辑思维能力和解决问题的能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的团队合作意识和自主学习能力。
四. 说教学重难点1.教学重点:特殊角的三角函数值的计算和应用。
2.教学难点:理解三角函数的定义,掌握特殊角的三角函数值的计算方法。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例分析法、小组合作法等,引导学生主动参与课堂,提高学生的学习兴趣和积极性。
2.教学手段:利用多媒体课件、数学软件、实物模型等,帮助学生直观地理解特殊角的三角函数值。
六. 说教学过程1.导入:通过回顾前置知识,引导学生进入三角函数的学习。
2.知识讲解:介绍特殊角的三角函数值,引导学生通过观察、思考、探究,理解并掌握这些知识。
3.案例分析:利用实际问题,让学生运用特殊角的三角函数值解决实际问题。
4.小组讨论:引导学生进行小组合作,共同探讨特殊角的三角函数值的计算方法。
5.总结提升:对特殊角的三角函数值进行总结,引导学生发现规律,提高解决问题的能力。
6.课堂练习:布置一些相关的练习题,让学生巩固所学知识。
北师大版数学九年级下册1.2《30、45、60的三角函数值》教学设计一. 教材分析北师大版数学九年级下册1.2《30、45、60的三角函数值》是三角函数基础知识的学习,本节课主要让学生了解特殊角的三角函数值,并通过实际问题引出三角函数的概念。
教材通过生活中的实例,引导学生探究并掌握30°、45°、60°角的正弦、余弦、正切函数值,培养学生动手操作、合作交流的能力。
二. 学情分析九年级的学生已经具备了一定的几何知识,对特殊角的三角函数值有一定的了解。
但学生对三角函数的概念和应用可能还比较模糊,因此,在教学过程中,教师需要通过生动形象的实例,引导学生理解和掌握三角函数的概念,以及30°、45°、60°角的三角函数值。
三. 教学目标1.了解三角函数的概念,理解30°、45°、60°角的正弦、余弦、正切函数值。
2.能够运用三角函数解决实际问题。
3.培养学生的动手操作能力、合作交流能力。
四. 教学重难点1.重点:掌握30°、45°、60°角的正弦、余弦、正切函数值。
2.难点:理解三角函数的概念,并能运用三角函数解决实际问题。
五. 教学方法1.情境教学法:通过生活中的实例,引导学生理解和掌握三角函数的概念。
2.合作学习法:引导学生分组讨论,共同探究30°、45°、60°角的三角函数值。
3.实践操作法:让学生动手操作,实际测量特殊角的三角函数值。
六. 教学准备1.准备相关的生活实例,用于引导学生理解三角函数的概念。
2.准备三角板、直尺等测量工具,让学生实际测量特殊角的三角函数值。
3.准备课堂练习题,用于巩固所学知识。
七. 教学过程1.导入(5分钟)教师通过一个生活中的实例,如修建楼房时,工人师傅需要知道楼高是否符合要求,引入三角函数的概念。
引导学生思考:如何计算楼高?引出本节课的主题——特殊角的三角函数值。
2024北师大版数学九年级下册1.2《特殊的三角函数值》教学设计一. 教材分析《特殊的三角函数值》是北师大版数学九年级下册第1.2节的内容,本节课主要让学生了解并掌握特殊角的三角函数值,包括30°、45°、60°角的正弦、余弦、正切值。
这些特殊角的三角函数值在实际生活和工作中有着广泛的应用,对于学生来说,掌握这些值能够提高他们解决实际问题的能力。
二. 学情分析九年级的学生已经学习了三角函数的基本概念,对于正弦、余弦、正切函数有一定的了解。
但是,对于特殊角的三角函数值,学生可能还没有完全掌握。
因此,在教学过程中,需要引导学生通过观察、思考、实践等方式,自主探索并掌握特殊角的三角函数值。
三. 教学目标1.知识与技能:让学生掌握30°、45°、60°角的正弦、余弦、正切值,并能运用这些值解决实际问题。
2.过程与方法:通过观察、思考、实践等方式,培养学生自主学习的能力和合作精神。
3.情感态度与价值观:激发学生对数学的兴趣,培养他们积极思考、勇于探索的精神。
四. 教学重难点1.教学重点:掌握30°、45°、60°角的正弦、余弦、正切值。
2.教学难点:特殊角三角函数值的推导和应用。
五. 教学方法1.情境教学法:通过生活实例,引导学生关注特殊角的三角函数值在实际生活中的应用。
2.启发式教学法:引导学生观察、思考、讨论,激发学生的学习兴趣和自主学习能力。
3.实践教学法:让学生通过动手操作,加深对特殊角三角函数值的理解。
六. 教学准备1.教学PPT:制作包含特殊角三角函数值的PPT,以便于课堂演示和讲解。
2.学习素材:准备与特殊角三角函数值相关的练习题,以便于课堂练习和巩固。
3.教学工具:准备三角板、直尺等工具,以便于学生实践操作。
七. 教学过程1.导入(5分钟)利用生活实例,如建筑工人测量高度、运动员投掷等,引导学生关注特殊角的三角函数值在实际生活中的应用。
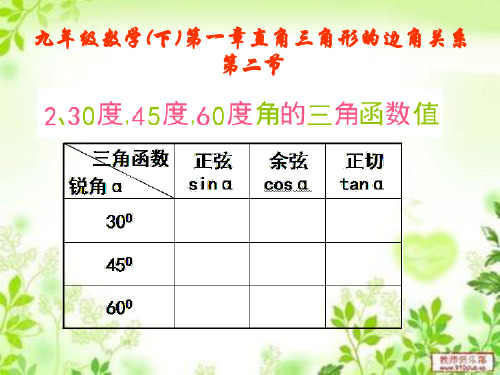
§1.2特殊角的三角函数
学习目标
1会计算含有30°、45°、60°角的三角函数的值. 2能根据30°、45°、60°角的三角函数值,说出相应锐角的大小. 重点、难点:掌握30°、45°、60°角的三角函数值,并运用它们进行计算。
学习过程
一、温故而知新
1.如图所示,在Rt △ABC 中,∠C =90°,
的邻边
A A ∠=
)
(
tan =______; 的邻边
B B ∠=
)(
tan =
; 斜边
)(
sin =
A =______,
斜边
)
(
sin =
B = ;
斜边
)
(
cos =
A =______;斜边
)
(
cos =
B = .
2.如图:P 是∠α的边OA 上一点,且P 点的坐标为(3,4), 则cos α=_______,sin α=_______,tan α=_______.
二、合作探究,发现新知
1.你能根据一副三角板,分别说出30°、45°、60°角的三角函数值吗?
2. 三、典例分享
例1:求下列各式的值.
(1)2sin30°-cos45° (2)sin60°·cos60° (3)sin 230°+cos 2
30°
练习:计算.
(1) cos45°-sin30° (2)sin 260°+cos 2
60° (3)tan45°-sin30°·cos60°
例2:一个小孩荡秋千,如图所示,秋千链子的长OA 为2.5米,当秋千向两边摆动时,摆角∠BOD 恰好是60°,并且两边摆动角度相同, 求:秋千摆至最高位置时与最低位置时的高度之差. (结果都精确到0.01)
c
b a A
B
C
四、当堂训练,巩固新知 1.计算
(1) sin60°-tan45° (2)cos60°+ tan60° (3) tan45°-sin30°
(4)2sin30°+3cos60°-4tan45° (5)
2
2
sin 45°+ sin60°-2cos 45°
2.某商场有一自动扶梯,其倾斜角为30°.高为7 m ,扶梯的长度是多少?
五、课后作业 1.计算
(1) cos60°+ sin45°-tan30° (2) 6tan 2
30°-3sin60°-2cos 45°
2.如图,河岸AD 、BC 互相平行,桥AB 垂直于两岸,桥长12 m ,从C 处看桥的两端A 、B ,夹角∠BCA=60°,求B 、C 之间的距离(结果精确到1m ).
3.SO 是等腰三角形的SAB 高,AS=BS ,已知∠BSA =120°,AB=54,求SO 的长。
4.如图,身高1.6m 的小丽用一个两锐角分别为30°和60°的三角尺
测量一棵树的高度,已知她与树之间的距离为6m ,那么这棵树高大 约高多少米?(结果精确到0.1m ,其中小丽眼睛距离地面高度近似 为身高)
5.若sin α=2
2,则锐角α=________. 若2cos α=1,则锐角α=_________. 6.求满足下列条件的锐角α: (1)cos α=
2
3
(2)2sin α=1 (3)2sin α-2=0 (4)3tan α-1=0。