常见符号含义
- 格式:pdf
- 大小:184.61 KB
- 文档页数:7
常用标点符号用法含义一、基本定义句子,前后都有停顿,并带有一定的句调,表示相对完整的意义。
句子前后或中间的停顿,在口头语言中,表现出来就是时间间隔,在书面语言中,就用标点符号来表示。
一般来说,汉语中的句子分以下几种:陈述句:用来说明事实的句子。
祈使句:用来要求听话人做某件事情的句子。
疑问句:用来提出问题的句子。
感叹句:用来抒发某种强烈感情的句子。
复句、分句:意思上有密切联系的小句子组织在一起构成一个大句子。
这样的大句子叫复句,复句中的每个小句子叫分句。
构成句子的语言单位是词语,即词和短语(词组)。
词即最小的能独立运用的语言单位。
短语,即由两个或两个以上的词按一定的语法规则组成的表达一定意义的语言单位,也叫词组。
标点符号是书面语言的有机组成部分,是书面语言不可缺少的辅助工具。
它帮助人们确切地表达思想感情和理解书面语言。
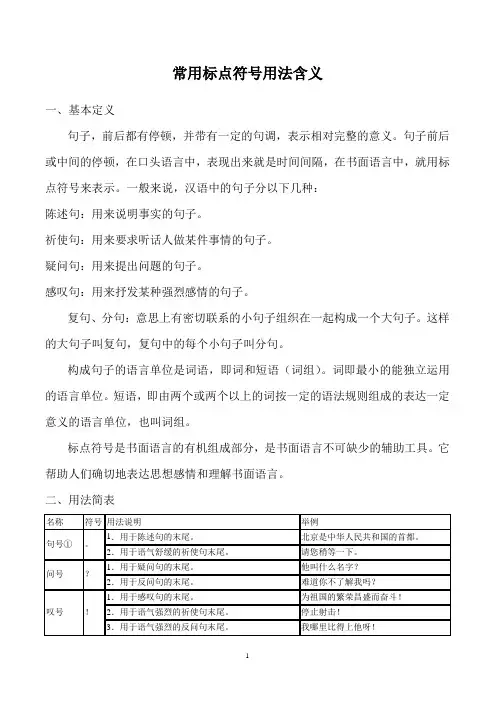
二、用法简表附注:①句号的形式为“。
”。
句号还有一种形式,即一个小圆点“.”,一般在科技文献中使用。
②非并列关系(如转折关系、因果关系等)的多重复句,第一层的前后两部分之间,也用分号。
③直行文稿引号改用双引号“﹄﹃”和单引号“﹂﹁”。
④此外还有方括号“[]”、六角括号“〔〕”、和方头括号“【】”。
⑤如果是整段文章或诗行的省略,可以使用十二个小圆点来表示。
⑥连接号还有另外三种形式,即长横“——”(占两个字的位置)、半字线“—”(占半个字的位置)、和浪纹“~”(占一个字的位置)。
⑦专名号只用在古籍或某些文史著作里面。
为了跟专名号配合,这类著作里的书名号可以用浪线“﹏﹏”。

数学符号常见数学符号及其含义数学符号在数学领域中起着非常重要的作用,它们代表着特定的数学概念、运算方法和数学公式。
了解这些常见的数学符号及其含义,对于学习和理解数学知识是至关重要的。
在本文中,我将为您介绍一些常见的数学符号及其含义。
1. 加号 (+)加号是最基本的数学符号之一,代表着两个数的相加运算。
例如,a +b 表示将数 a 和数 b 相加。
2. 减号 (-)减号是一个表示减法运算的符号。
例如,a - b 表示将数 a 减去数 b。
3. 乘号 (×)乘号是表示乘法运算的符号。
例如,a × b 表示将数 a 与数 b 相乘。
4. 除号 (÷)除号是表示除法运算的符号。
例如,a ÷ b 表示将数 a 除以数 b。
5. 等号 (=)等号用于表示两个数或表达式相等。
例如,a = b 表示 a 和 b 是相等的。
6. 不等号(≠)不等号用于表示两个数或表达式不相等。
例如,a ≠ b 表示 a 和 b 不相等。
7. 大于号 (>)大于号表示一个数大于另一个数。
例如,a > b 表示 a 大于 b。
8. 小于号 (<)小于号表示一个数小于另一个数。
例如,a < b 表示 a 小于 b。
9. 大于等于号(≥)大于等于号表示一个数大于或等于另一个数。
例如,a ≥ b 表示 a 大于或等于 b。
10. 小于等于号(≤)小于等于号表示一个数小于或等于另一个数。
例如,a ≤ b 表示 a 小于或等于 b。
11. 括号 ( )括号用于改变运算的顺序和优先级。
例如,(a + b) × c 表示先将 a和 b 相加,再将结果乘以 c。
12. 平方根(√)平方根符号表示一个数的非负平方根。
例如,√a 表示数 a 的平方根。
13. 指数 (^)指数符号表示一个数的乘方运算。
例如,a^b 表示将数a 自乘b 次。
14. 百分号 (%)百分号用于表示一个数除以 100 的结果。

数学符号的含义
+:加号
-:减号
×:乘号
÷:除号
≈:约等于符号
∈:属于符号,表示元素与集合之间的一种从属关系
∏:求积符号
∑:求和符号
∕:相当于除号÷
√:算术平方根,如±2的平方是4,那么4的算术平方根是2
∝:正比于,常见于物理学,如a∝b说明当a增加,b也增加
∞:无穷,表示一种趋向,+∞表示不断变大的趋势
∟:直角符号
∠:角符号
∣:绝对值符号
‖:平行,刻画两直线的关系
∨:并符号,逻辑差不多符号,表示两个命题有一个发生那么命题成立
∩:交符号:集合差不多符号,表示两个集合同时满足
∪:并符号,集合差不多符号,表示至少满足一个集合
∫:不定积分符号,微积分差不多符号
∮:积分符号,微积分差不多符号
∴:因此
∵:因为
∶:比例符号
∷:比例
∽:相似符号,刻画图形之间的关系
≌:全等符号,刻画图形之间的关系
≠:不等号
≡:恒等与同余符号,数论差不多符号,表示两个整数除以同一个特定的整数余数相等,例如5=2×2+1,7=2×3+1,那么5≡7(mod2)
≤:不大于,关系符号,前者小于或者等于后者
≥:不小于,关系符号,前者大于或者等于后者
≮:非小于同≥
≯:非大于同≤
⊙:圆,⊙O表示圆心为O的圆
⊥:垂直
⊿:三角形
sin:正弦函数
Cos:余弦函数
tan:正切函数
cot:余切函数
sec:正割函数
csc:余割函数log:对数
ln:自然对数lg:常用对数。

数学所有的符号数学是一种精密、抽象和逻辑性极强的学科,而符号是数学中至关重要的元素之一。
符号用来表示数学概念、关系和操作,使得数学中的复杂问题的表达和解决得以变得简单而准确。
在这篇文章中,我们将探讨数学中一些常见的符号及其含义。
一、基础符号1. 加号(+)加号是数学中最基本的符号之一,表示两个数或两个量的和。
例如,“3+4”表示3和4的和,结果为7。
同样,我们可以使用加号来表示更多的数或量的和,例如“2+5+1+3+9”表示这五个量的和为20。
2. 减号(-)减号也是常见的符号,表示一个数或一个量减去另一个数或量。
例如,“6-3”表示6减去3,结果为3。
类似地,“5-2-1”表示首先将5减去2,然后再减去1,结果为2。
3. 乘号(×)乘号用来表示两个数或两个量的乘积。
例如,“3×4”表示3和4的乘积,结果为12。
同样,“2×5×1×3×9”表示这五个量的乘积为270。
4. 除号(÷)除号用来表示一个数或量除以另一个数或量。
例如,“8÷2”表示将8分成2份,每份为4,结果为4。
同样,“20÷4÷2”表示首先将20分成4份,每份为5,然后将这5分之一再分成2份,每份为2.5,结果为2.5。
5. 等于号(=)等于号用来表示两个量相等。
例如,“3+4=7”表示3加4的结果等于7。
随后在数学中,等于号的应用变得更加广泛,在各种方程、恒等式和不等式的表达中都有重要的应用。
6. 大于号(>)大于号用来表示一个数或者量比另一个数或量大。
例如,“5>3”表示5比3大,为真。
另外,“x>y”表示x比y大,其中x和y可以是任何量或变量。
7. 小于号(<)小于号用来表示一个数或者量比另一个数或量小。
例如,“2<9”表示2比9小,为真。
同样,“y<x”表示y比x小,其中x和y可以是任何量或变量。

常用的特殊符号大全特殊符号是我们在日常书写和表达中经常使用的,它们可以用来表示特定的意义、注释或者增加文本的可读性。
下面是一些常见的特殊符号的大全:1. 标点符号:- 句号(.):用于句子的结束。
- 逗号(,):用于分隔句子中的短语或列表项。
- 分号(;):用于分隔较长的独立子句或列举项。
- 冒号(:):用于引导解释、说明或列举。
- 感叹号(!):用于表示强烈的情感或惊讶。
- 问号(?):用于表示疑问或询问。
2. 引号:- 双引号(''):用于引用直接的对话、引文或特定的词语。
- 单引号(''):用于引用间接的对话或特定的词语。
3. 括号:- 圆括号(()):用于插入补充说明或解释的内容。
- 方括号([]):用于引用或注释文本。
- 大括号({}):用于表示集合、分组或约束条件。
4. 运算符:- 加号(+):用于表示加法运算。
- 减号(-):用于表示减法运算。
- 乘号(×):用于表示乘法运算。
- 除号(÷):用于表示除法运算。
- 等号(=):用于表示相等关系。
- 大于号(>)和小于号(<):用于表示大小关系。
- 百分号(%):用于表示百分比。
5. 特殊符号:- 版权符号():用于表示版权所有。
- 注册商标符号():用于表示商标注册。
- 电话号码符号():用于表示电话联系方式。
- 心形符号():用于表示爱或喜欢。
- 笑脸符号():用于表示愉快或开心的表情。
- 禁止符号():用于表示禁止或不允许。
这些是一些常见的特殊符号的大全,它们在我们的书写和表达中起到了重要的作用。
熟练地使用这些符号能够让我们的文本更加丰富多样,增强交流的效果。

符号的含义和用法
1. 嘿,你知道感叹号吧!它就像一个情绪放大器!比如,“哇,今天天气真好!”这里的感叹号是不是一下子就把那种惊喜的感觉表现出来啦。
2. 问号呀,那可是我们寻求答案的好帮手呢!像“你今天吃了啥?”这简单的一问,就表达了我们对别人情况的好奇嘛。
3. 引号可有意思啦,它就像个展示柜!比如说“他说‘我马上就来’”,就把特定的话语给凸显出来了。
4. 破折号呢,就像是个解释小天使哟!像“我最喜欢的颜色——蓝色”,后面就对前面进行了具体的说明呢。
5. 省略号啊,就像留给人无限遐想的小窗口!比如“他欲言又止……”,让人特别想知道他到底想说啥呢。
6. 逗号就像个短暂的停顿按钮!“我今天去了超市,买了很多东西。
”它让句子读起来更顺畅呢。
7. 分号可以把不同的部分分隔开呀,就像划分区域一样!“我喜欢红色;他喜欢蓝色。
”这样是不是很清楚。
8. 冒号呢,就如同一盏指路明灯!“下面我要说一件重要的事:明天要考试啦!”是不是马上就知道重点来了。
9. 括号呢,哎呀,就像是个小注释!比如“他很厉害(真的超级厉害)”,这里面的内容就是对前面的补充说明呀。
我觉得这些符号真的是太神奇啦,它们让我们的表达更加丰富多彩呢!。

物理化学中的符号及其含义在物理化学中,符号是一种广泛使用的表示物理和化学性质的方式。
符号通常由字母、数字和点号组成,具有特定的含义。
以下是一些常见的符号及其含义:1. Q:表示热量,符号为 Q。
它表示物质在热力学过程中所吸收或释放的热量。
2. W:表示功,符号为 W。
它表示物体在力的作用下所做的功。
3. F:表示力,符号为 F。
它表示物体所受到的力。
4. Qe:表示逸出功,符号为 Qe。
它表示物体从高温处吸收的热量,用于克服外部阻力而使物体温度降至低温处。
5. Φ:表示磁通量,符号为Φ。
它表示磁场中某一点的磁通量。
6. t:表示时间,符号为 t。
它表示物理过程所经历的时间。
7. D:表示扩散,符号为 D。
它表示物质在空间中的扩散程度。
8. L:表示长度,符号为 L。
它表示物理过程中所涉及物体的长度。
9. V:表示体积,符号为 V。
它表示物理过程中所涉及物体的体积。
10. p:表示压强,符号为 p。
它表示物体内部的压力。
11. o:表示标准状况,符号为 o。
它表示压强、温度和体积均为标准值的状况。
12. t1:表示低温状态,符号为 t1。
它表示物理过程中的某个状态,低温状态通常指物体的温度低于环境温度。
13. t2:表示高温状态,符号为 t2。
它表示物理过程中的某个状态,高温状态通常指物体的温度高于环境温度。
这些符号是物理化学中最常见的符号之一。
理解这些符号的含义对于理解物理和化学过程非常重要。

高中数学符号读法大全及意义一、基本数学符号1. +:加号,表示加法运算。
2. -:减号,表示减法运算。
3. ×:乘号,表示乘法运算。
4. ÷:除号,表示除法运算。
5. =:等于号,表示相等关系。
6. ≠:不等号,表示不相等关系。
7. <:小于号,表示小于关系。
8. >:大于号,表示大于关系。
9. ≤:小于等于号,表示小于等于关系。
10. ≥:大于等于号,表示大于等于关系。
二、集合符号1. ∈:属于,表示一个元素属于某个集合。
2. ∉:不属于,表示一个元素不属于某个集合。
3. ∪:并集,表示所有在某一个以上的集合中出现的元素的新集合。
4. ∩:交集,表示属于所有给定集合的元素的新集合。
5. ⊆:包含关系(子集),表示一个集合包含于另一个集合。
6. ⊇:包含关系(超集),表示一个集合包含另一个集合。
7. ∅:空集,表示没有任何元素的集合。
三、数学函数符号1. f(x):函数符号,表示自变量为x时,函数的值。
2. g(x):函数符号,表示自变量为x时,函数的值。
3. h(x):函数符号,表示自变量为x时,函数的值。
4. lim:极限符号,表示函数在逼近某个数值时的极限。
5. sin:正弦函数符号,表示角度的正弦值。
6. cos:余弦函数符号,表示角度的余弦值。
7. tan:正切函数符号,表示角度的正切值。
8. log:对数函数符号,表示以某个底数为底的对数函数。
四、微积分符号1. dy/dx:导数符号,表示某个函数在某点的导数。
2. ∫:积分符号,表示函数在某个区间上的积分值。
3. dx:微分符号,表示微分变量。
4. Δx:增量符号,表示微分变量的增量。
五、几何图形符号1. ∆ABC:三角形符号,表示三条边分别为AB、BC和CA的三角形。
2. △DEF:三角形符号,表示三条边分别为DE、EF和FD的三角形。
3. ∠:角符号,表示两条射线之间的角度。
4. ⊥:垂直符号,表示两条直线垂直。

常用的数学符号大全及其意义在数学中,有许多常用的符号用来表示数学概念、运算和关系。
以下是一些常见的数学符号及其意义的详细介绍:1.+(加号):表示两个数的加法运算,如2+3=52.-(减号):表示两个数的减法运算,如5-2=33.×(乘号):表示两个数的乘法运算,如2×3=64.÷(除号):表示两个数的除法运算,如6÷2=35.=(等号):表示两个数或表达式相等的关系,如2+3=56.<(小于号):表示一个数小于另一个数的关系,如3<57.>(大于号):表示一个数大于另一个数的关系,如5>38.≤(小于等于号):表示一个数小于或等于另一个数的关系,如3≤59.≥(大于等于号):表示一个数大于或等于另一个数的关系,如5≥310.≠(不等号):表示两个数或表达式不相等的关系,如2+3≠611.():圆括号,用于表示运算的优先级或改变表达式的结构,如(2+3)×412.[]:方括号,用于表示数集或矩阵等,如[1,2,3]。
13.{}:花括号,用于表示集合的元素或条件,如{1,2,3}。
14.√(开方号):表示一个数的平方根,如√9=315.^(上标):表示一个数的幂运算,如2^3=816. ∞(无穷大):表示一个数趋近于无穷大的概念,如lim(x→∞) = ∞。
17.∑(求和符号):表示一系列数的累加和,如∑(1,2,3)=1+2+318. ∫(积分符号):表示曲线下的面积或函数的积分运算,如∫(0, 1) x^2 dx。
21.∠(角度符号):表示一个角度的概念,如∠ABC表示角ABC。
22.∥(平行符号):表示两条直线平行的关系,如AB∥CD。
23.⊥(垂直符号):表示两条直线垂直的关系,如AB⊥CD。
24.∆(三角形符号):表示一个三角形的概念,如∆ABC表示三角形ABC。
25.∝(正比符号):表示两个量之间成正比的关系,如y∝x表示y与x成正比。

象征符号举例1. 引言符号是人类语言和文化传播的重要工具,它们通过简洁、直观的形式表达特定的意义和概念。
象征符号作为一种特殊类型的符号,具有更加深远的意义和影响力。
本文将介绍一些常见的象征符号,并探讨它们在不同文化背景下所代表的含义。
2. 世界各地常见的象征符号2.1 和平符号(☮)和平符号是一种广为人知的象征,它由一个圆圈和一个向下倾斜的拉丁字母”N”组成。
这个符号起源于上世纪60年代美国反战运动,代表着反对暴力、追求和平与爱的理念。
如今,这个符号已经成为全球范围内抗议战争、呼吁和平与友谊的标志。
2.2 爱心符号(☮)爱心符号是象征爱情和情感的代表。
它通常是一个红色的心形图案,代表着热爱、关怀和友谊。
这个符号在世界各地都被广泛使用,不仅用于表示恋爱关系,还用于表达亲情、友情等各种深厚的情感。
2.3 幸运四叶草(☮)幸运四叶草是一种象征好运和幸福的符号。
它由三片典型的三叶草叶片加上一个罕见的第四片组成。
在西方文化中,人们相信找到一片四叶草会带来好运和幸福。
因此,这个符号常常被用作护身符或装饰品。
2.4 生命之树(?)生命之树是一种具有宗教和哲学意义的象征。
它通常由一个大树的形象组成,树冠延伸至天空,树根扎入地下。
生命之树代表着生命的起源、成长和繁荣,同时也象征着人类与自然的紧密联系。
3. 象征符号在不同文化中的意义3.1 中文文化中的象征符号在中国文化中,一些象征符号具有特殊的意义。
例如:•龙:龙是中国传统文化中最具象征性的符号之一,代表着权力、尊贵和吉祥。
•凤凰:凤凰是另一个重要的中国象征符号,被视为吉祥、幸福和美好未来的象征。
•红色:红色在中国文化中象征着喜庆、吉祥和幸福。
3.2 印度文化中的象征符号印度文化也有许多独特而富有象征意义的符号。
例如:•奥姆(ॐ):奥姆是印度教和佛教中最重要的象征之一,代表着宇宙的起源和无限。
•斯瓦斯蒂卡(卍):斯瓦斯蒂卡是印度教中的吉祥符号,象征着幸福、繁荣和好运。

数学定义中的符号有许多种,以下是一些常见的符号及其含义:
1. 几何符号:⊥ 表示垂直,∥ 表示平行,∠ 表示角度,⌒ 表示圆弧,⊙ 表示圆,≡ 表示全等,≌ 表示全等于,△ 表示三角形。
2. 代数符号:∝ 表示成正比,∧ 表示乘方,∨ 表示幂运算,~表示等价,∫ 表示积分,≠ 表示不等于,≤ 表示小于等于,≥ 表示大于等于,≈ 表示近似,∞ 表示无穷大,∶ 表示比值。
3. 运算符号:+表示加法,-表示减法,×或·表示乘法,÷或/表示除法,∪表示并集,∩表示交集,√表示根号,log、lg、ln表示对数,∶表示比值,dx表示微分,∫表示积分,∮表示曲线积分。
4. 关系符号:=表示等于,≈表示近似等于,≠表示不等于,>表示大于,<表示小于,≥表示大于或等于(也可写作≮),≤表示小于或等于(也可写作≯)。
5. 特殊符号:π表示圆周率,√ ̄表示根号下,℃表示摄氏度。
以上仅是数学定义中的部分符号,数学符号非常丰富,具体内容建议咨询数学老师或查阅相关书籍。
生活中的符号及意义
1.红色十字:这个符号通常与医疗和紧急情况有关。
它代表了紧急医
疗救护、血液和生命的重要性。
在许多文化中,这个符号也被视为好运和避邪的象征。
2.圆圈加斜线:这个符号是“禁止”或“不允许”的标志,通常用于表示
不允许进入、禁止吸烟、禁止拍照等场合。
3.圆圈加一个点:这个符号代表“安全出口”或“紧急出口”,通常用于
指示逃生路径。
4.三角形:在交通标志中,三角形通常表示警告或提醒,如前方有交
叉路口、弯道、学校等。
5.方形:方形通常表示“请勿进入”、“停车场”或“行人禁止进入”等意
思。
6.菱形:菱形通常用于指示停车或者减速行驶。
7.倒三角形:这个符号表示“请勿打扰”或者“私人空间”,常见于酒店
房间门牌号或者公共场所。
8.枫叶形:这个符号表示“残疾人专用”,常见于公共交通工具上或者
公共场所。
9.叉形:叉形通常表示“禁止”或者“不允许”,如禁止停车、禁止携带
违禁品等。
10.勺子形:这个符号表示“餐饮”或者“饭店”,常见于路标或者广告牌
上。
网名符号大全在网络世界中,网名是每个人的虚拟身份,它不仅是一个标识,更是一种个性的展现。
而网名符号,则是丰富网名的一种方式,它可以让网名更加独特、有趣。
下面就让我们来一起了解一些常见的网名符号吧!1. 符号,❤️。
含义,爱心。
用途,表达爱意、喜欢、善良等情感。
2. 符号,❤️。
含义,太阳。
用途,象征阳光、热情、希望等。
3. 符号,✨。
含义,星星。
用途,代表闪耀、美好、梦想等。
4. 符号,♠️。
含义,黑桃。
用途,代表冷酷、神秘、力量等。
5. 符号,❤️。
含义,云。
用途,表达悠闲、轻松、清新等情绪。
6. 符号,❤️。
含义,回收。
用途,象征环保、可持续发展等。
7. 符号,❤️。
含义,和平。
用途,代表和平、友爱、和谐等。
8. 符号,❤️。
含义,胜利手势。
用途,表达胜利、和平、自由等。
9. 符号,❤️。
含义,阴阳。
用途,代表平衡、和谐、哲学等。
10. 符号,❤️。
含义,彗星。
用途,象征奇迹、改变、希望等。
以上是一些常见的网名符号,它们可以让你的网名更加生动、富有个性。
当然,除了这些符号,还有许多其他的符号可以使用,你可以根据自己的喜好和个性来选择适合自己的网名符号。
在选择网名符号时,不妨多加思考,尽量选择与自己个性相符合的符号,这样才能更好地展现自己的个性和情感。
同时,也要注意符号的使用不要过多,以免显得过于花哨或繁杂。
总之,网名符号是网名的点睛之笔,它能够为你的网名增添一份特别的魅力。
希望以上介绍的网名符号能够给你带来一些灵感,让你在选择网名符号时更加得心应手。
祝你找到最适合的网名符号,展现出最独特的个性!。
常见的数学符号及其含义在数学中,符号是一种用来表示特定概念或关系的标记。
熟悉常见的数学符号及其含义对于理解和应用数学知识至关重要。
本文将介绍一些常见的数学符号及其含义。
一、基本运算符号1. 加法符号(+):用来表示两个数的相加操作,例如 3 + 4 = 7。
2. 减法符号(-):用来表示两个数的相减操作,例如 6 - 2 = 4。
3. 乘法符号(×或 *):用来表示两个数的相乘操作,例如 2 × 5 = 10。
4. 除法符号(÷或 /):用来表示两个数的相除操作,例如 8 ÷ 4 = 2。
二、关系符号1. 等于符号(=):用来表示两个数或表达式相等的关系,例如 2 + 3 = 5。
2. 大于符号(>):用来表示某个数大于另一个数的关系,例如 7 > 5。
3. 小于符号(<):用来表示某个数小于另一个数的关系,例如 3 < 6。
4. 大于等于符号(≥):用来表示某个数大于或等于另一个数的关系,例如4 + 2 ≥ 6。
5. 小于等于符号(≤):用来表示某个数小于或等于另一个数的关系,例如 8 - 3 ≤ 5。
三、代数符号1. 变量(通常用字母表示):代表未知数或可变的数值,例如在代数表达式中,a + b = c,其中 a、b 和 c 都是变量。
2. 参数(例如 a、b、c):代表函数中的输入值。
3. 系数(例如 3、4、5):代表带有变量的数。
四、集合符号1. 集合符号({}):用来表示一组元素的集合,例如 {1, 2, 3} 表示由元素 1、2 和 3 组成的集合。
2. 元素属于符号(∈):用来表示某个元素属于某个集合,例如 2 ∈ {1, 2, 3}。
3. 元素不属于符号(∉):用来表示某个元素不属于某个集合,例如 4 ∉ {1, 2, 3}。
五、指数符号1. 幂符号(^):用来表示某个数的幂运算,例如 2^3 表示 2 的 3 次方,即 2 × 2 × 2 = 8。
各种数学符号及读法大全数学是一门充满魅力和奥秘的学科,而数学符号则是这门学科中不可或缺的重要元素。
它们简洁明了地表达着复杂的数学概念和运算,是数学交流和表达的有力工具。
接下来,让我们一起走进数学符号的世界,了解它们的读法和含义。
一、基本运算符号1、加号(+):读作“加”,表示两个或多个数量的总和。
例如,“2 +3”读作“二加三”。
2、减号():读作“减”,表示两个数量之间的差值。
比如,“5 2”读作“五减二”。
3、乘号(×):读作“乘”,表示两个或多个数量的乘积。
“3 × 4”读作“三乘四”。
4、除号(÷):读作“除以”,表示一个数量被另一个数量平均分。
“10 ÷ 2”读作“十除以二”。
二、比较符号1、等于号(=):读作“等于”,表示两个数量或表达式的值相等。
“5 =5”读作“五等于五”。
2、大于号(>):读作“大于”,表示左边的数量大于右边的数量。
“7 >5”读作“七大于五”。
3、小于号(<):读作“小于”,表示左边的数量小于右边的数量。
“3 <8”读作“三小于八”。
4、大于等于号(≥):读作“大于等于”,表示左边的数量大于或等于右边的数量。
“6≥ 5”读作“六大于等于五”。
5、小于等于号(≤):读作“小于等于”,表示左边的数量小于或等于右边的数量。
“4 ≤ 7”读作“四小于等于七”。
三、括号1、小括号(()):读作“括号”,用于改变运算的顺序。
例如,“(2 +3) × 4”先计算括号内的加法,再进行乘法运算。
2、中括号():读作“中括号”,在复杂的表达式中用于进一步明确运算顺序。
3、大括号({}):读作“大括号”,常用于集合的表示等。
四、分数符号1、分数线(—):上面的数字称为分子,下面的数字称为分母。
例如,“3/5”读作“五分之三”。
2、带分数:由整数部分和分数部分组成,例如“2 又1/3”读作“二又三分之一”。
五、指数符号1、上标数字:表示指数,例如“2³”读作“二的三次方”,表示 2 × 2× 2。
常用数学符号的读法及其含义
1. 嘿,你知道“=”这个符号吧,它读作“等于”呀!比如说,
“1+1=2”,这就表示两边是相等的呀!这多简单明了,要是没有它,我们可怎么表达相等的概念呢?
2. 哇塞,“>”这个符号读作“大于”呢!就像 5>3,这不是很直白地告诉我们 5 比 3 要大嘛,它可太重要啦!
3. 哈哈,“<”就是“小于”呀!比如 2<4,一下子就能看出 2 是小于 4 的呀,没有它可不行哦!
4. “+”呀,读“加”!想想看,2+3=5,它就是把数字加在一起的意思呀,多神奇!
5. “-”呢,当然是“减”啦!像 5-3=2,它让我们能做减法运算呢,是不是很厉害?
6. “×”这个符号读作“乘”哟!比如3×4=12,乘法可少不了它呀!
7. “÷”就是“除”啦!像12÷3=4,没有它除法可就没法表示啦,对吧?
8. “π”呀,读“派”,它可是个很特别的符号呢!在计算圆的周长和面积时经常用到它呢,厉害吧!
9. “%”读作“百分之”,像 50%就是一半呀!在表示比例的时候经常出现呢,很实用呀!
10. 最后说说“!”,它读作“阶乘”哦!比如 5!就是
5×4×3×2×1,是不是很有意思呀!
我的观点结论就是:这些数学符号真的太重要啦,它们是数学世界的基石呀,没有它们数学可就没法玩啦!。
常用数学符号读法大全以及主要数学符号含义大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita 西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μμmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omi kron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon 衣普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧米伽数学符号:(1)数量符号:如:i,2+i,a,x,自然对数底e,圆周率π.(2)运算符号:如加号(+),减号(-),乘号(×或·),除号(÷或/),两个集合的并集(∪),交集(∩),根号(√),对数(log,lg,ln),比(:),微分(dx),积分(∫)等.(3)关系符号:如“=”是等号,“≈”是近似符号,“≠”是不等号,“>”是大于符号,“<”是小于符号,“→”表示变量变化的趋势,“∽”是相似符号,“≌”是全等号,“∥”是平行符号,“⊥”是垂直符号,“∝”是反比例符号,“∈”是属于符号,“C”或“C下面加一横”是“包含”符号等.(4)结合符号:如圆括号“()”方括号“[]”,花括号“{}”括线“—”(5)性质符号:如正号“+”,负号“-”,绝对值符号“‖”(6)省略符号:如三角形(△),正弦(sin),余弦(cos),x的函数(f(x)),极限(lim),因为(∵),所以(∴),总和(∑),连乘(∏),从n个元素中每次取出r个元素所有不同的组合数(C(r)(n) ),幂(A,Ac,Aq,x^n),阶乘(!)等.数学符号的意义符号意义∞无穷大π圆周率|x|绝对值∪并集∩交集≥大于等于≤小于等于≡恒等于或同余ln(x)以e为底的对数lg(x)以10为底的对数floor(x)上取整函数ceil(x)下取整函数x mod y求余数x - floor(x) 小数部分∫f(x)dx不定积分∫[a:b]f(x)dx a到b的定积分→等价于趋向于数学符号的应用P为真等于1否则等于0∑[1≤k≤n]f(k) 对n进行求和,可以拓广至很多情况如:∑[n is prime][n < 10]f(n)∑∑[1≤i≤j≤n]n^2lim f(x) (x->?) 求极限f(z) f关于z的m阶导函数C(n:m) 组合数,n中取mP(n:m) 排列数m|n m整除nm⊥n m与n互质a ∈A a属于集合A#A 集合A 中的元素个数“∑”数学里的连加符号,叫西格马,求和的意思要给出上下界限(比如k是自然数∑k(上界限至n,下界限从k=0开始) ∑k=0+1+2+……+n {大括号(bracket)是用来规定运算次序的符号。