计量经济学第七章 分布滞后模型与自回归模型.

第五章 异方差性思考题5.1 简述什么是异方差？为什么异方差的出现总是与模型中某个解释变量的变化有关？答 ：设模型为),....,,(....n 21i X X Y i i 33i 221i =μ+β++β+β=，如果其他假定均不变，但模型中随机误差项的方差为),...,,()(n 21i Var 2i i =σ=μ，则称i μ具有异方差性。

由于异方差性指的是被解释变量观测值的分散程度是随解释变量的变化而变化的，所以异方差的出现总是与模型中某个解释变量的变化有关。

5.2 试归纳检验异方差方法的基本思想，并指出这些方法的异同。

答：各种异方差检验的共同思想是，基于不同的假定，分析随机误差项的方差与解释变量之间的相关性，以判断随机误差项的方差是否随解释变量变化而变化。

其中，戈德菲尔德-跨特检验、怀特检验、ARCH 检验和Glejser 检验都要求大样本，其中戈德菲尔德-跨特检验、怀特检验和Glejser 检验对时间序列和截面数据模型都可以检验，ARCH 检验只适用于时间序列数据模型中。

戈德菲尔德-跨特检验和ARCH 检验只能判断是否存在异方差，怀特检验在判断基础上还可以判断出是哪一个变量引起的异方差。

Glejser 检验不仅能对异方差的存在进行判断，而且还能对异方差随某个解释变量变化的函数形式进行诊断。

5.3 什么是加权最小二乘法？它的基本思想是什么？答：以一元线性回归模型为例：12i i i Y X u ββ=++经检验i μ存在异方差，公式可以表示为22var()()i i i u f X σσ==。

选取权数 i w ，当2i σ 越小 时，权数i w 越大。

当 2i σ越大时，权数i w 越小。

将权数与 残差平方相乘以后再求和，得到加权的残差平方和：2i 21i 2i i X Y w e w )(**β-β-=∑∑，求使加权残差平方和最小的参数估计值**ˆˆ21ββ和。

这种求解参数估计式的方法为加权最小二乘法。

计量经济学复习知识点重点难点计量经济学知识点第一章导论1、计量经济学的研究步骤：模型设定、估计参数、模型检验、模型应用。

2、计量经济学是统计学、经济学和数学的结合。

3、计量经济学作为经济学的一门独立学科被正式确立的标志：1930年12月国际计量经济学会的成立。

4、计量经济学是经济学的一个分支学科。

第二章简单线性回归模型1、在总体回归函数中引进随机扰动项的原因：①作为未知影响因素的代表；②作为无法取得数据的已知因素的代表；③作为众多细小影响因素的综合代表；④模型的设定误差；⑤变量的观测误差；⑥经济现象的内在随机性。

2、简单线性回归模型的基本假定：①零均值假定；②同方差假定；③随机扰动项和解释变量不相关假定；④无自相关假定；⑤正态性假定。

3、OLS回归线的性质：①样本回归线通过样本均值；②估计值的均值等于实际值的均值；③剩余项ei的均值为零；④被解释变量的估计值与剩余项不相关；⑤解释变量与剩余项不相关。

4、参数估计量的评价标准：无偏性、有效性、一致性。

5、OLS估计量的统计特征：线性特性、无偏性、有效性。

6、可决系数R2的特点：①可决系数是非负的统计量；②可决系数的取值范围为[0,1]；③可决系数是样本观测值的函数，可决系数是随抽样而变动的随机变量。

第三章多元线性回归模型1、多元线性回归模型的古典假定：①零均值假定；②同方差和无自相关假定；③随机扰动项和解释变量不相关假定；④无多重共线性假定；⑤正态性假定。

2、估计多元线性回归模型参数的方法：最小二乘估计、极大似然估计、矩估计、广义矩估计。

3、参数最小二乘估计的性质：线性性质、无偏性、有效性。

4、可决系数必定非负，但是根据公式计算的修正的可决系数可能为负值，这时规定为0。

5、可决系数只是对模型拟合优度的度量，可决系数越大，只是说明列入模型中的解释变量对被解释变量的联合影响程度越大，并非说明模型中各个解释变量对被解释变量的影响程度也大。

6、当R2=0时，F=0；当R2越大时，F值也越大；当R2=1时，F→∞。

练习题7.1参考解答（1）先用第一个模型回归，结果如下：22216.4269 1.008106 t=(-6.619723) (67.0592)R 0.996455 R 0.996233 DW=1.366654 F=4496.936PCE PDI =-+==利用第二个模型进行回归，结果如下：122233.27360.9823820.037158 t=(-5.120436) (6.970817) (0.257997)R 0.996542 R 0.996048 DW=1.570195 F=2017.064t t t PCE PDI PCE -=-++==（2)从模型一得到MPC=1.008106；从模型二得到，短期MPC=0.982382，长期MPC= 0.982382+(0.037158)=1.01954 练习题7.2参考答案（1）在局部调整假定下，先估计如下形式的一阶自回归模型：*1*1*0*t t t t u Y X Y +++=-ββα 估计结果如下：122ˆ15.104030.6292730.271676 se=(4.72945) (0.097819) (0.114858)t= (-3.193613) (6.433031) (2.365315)R =0.987125 R =0.985695 F=690.0561 DW=1.518595t t t Y X Y -=-++根据局部调整模型的参数关系，有****11 ttu u αδαβδββδδ===-=将上述估计结果代入得到： *1110.2716760.728324δβ=-=-=*20.738064ααδ==-*0.864001ββδ==故局部调整模型估计结果为：*ˆ20.7380640.864001ttYX =-+ 经济意义解释：该地区销售额每增加1亿元，未来预期最佳新增固定资产投资为0.864001亿元。

运用德宾h 检验一阶自相关：(121(1 1.34022d h =-=-⨯=在显著性水平05.0=α上，查标准正态分布表得临界值21.96h α=，由于21.3402 1.96h h α=<=，则接收原假设0=ρ，说明自回归模型不存在一阶自相关。

第七章 分布滞后模型与自回归模型一、判断题1. 无限分布滞后模型不可以转换为一阶自回归模型。

（ F ）2. 局部调整模型变换后得到的一阶自回归模型可以应用OLS 法估计。

（ T ）3. 估计自回归模型的问题仅在于滞后被解释变量的存在可能导致它与随机扰动项相关。

（F ）4. 自回归模型的产生背景都是相同的。

（ F ）5. 库伊克模型和自适应预期模型都存在解释变量与随机扰动项相关问题。

（ T ） 二、单项选择题1．设无限分布滞后模型为t 0t 1t-12t-2t Y = + X + X +X ++ U αβββ，且该模型满足Koyck 变换的假定，则长期影响系数为（ C ）。

A ．0βλB ． 01βλ+C ．01βλ- D ．不确定 2．对于分布滞后模型，时间序列的序列相关问题，就转化为（ B ）。

A ．异方差问题B ．多重共线性问题C ．多余解释变量D ．随机解释变量3．在分布滞后模型01122t t t t t Y X X X u αβββ--=+++++中，短期影响乘数为（ D ）。

A ．11βα- B ． 1β C ．01βα- D ．0β 4．对于自适应预期模型变换后的自回归模型，估计模型参数应采用( D ) 。

A ．普通最小二乘法B ．间接最小二乘法C ．二阶段最小二乘法D ．工具变量法5．经过库伊克变换后得到自回归模型，该模型参数的普通最小二乘估计量是( D ) 。

A ．无偏且一致B ．有偏但一致C ．无偏但不一致D ．有偏且不一致6．下列属于有限分布滞后模型的是（ D ）。

A ．01122t t t t t Y X Y Y u αβββ--=+++++B ．01122t t t t k t k t Y X Y Y Y u αββββ---=++++++ C ． 01122t t t t t Y X X X u αβββ--=+++++ D ．01122t t t t k t k t Y X X X X u αββββ---=++++++7．消费函数模型12ˆ4000.50.30.1t t t t C I I I --=+++，其中I 为收入，则当期收入t I 对未来消费2t C +的影响是：t I 增加一单位，2t C +增加（ C ）。

计量经济学复习笔记CH1导论1、计量经济学：以经济理论和经济数据的事实为依据，运用数学、统计学的方法，通过建立数学模型来研究经济数量关系和规律的一门经济学科。

研究主体是经济现象及其发展变化的规律。

2、运用计量分析研究步骤：模型设定——确定变量和数学关系式估计参数——分析变量间具体的数量关系模型检验——检验所得结论的可靠性模型应用——做经济分析和经济预测3、模型变量:解释变量:表示被解释变量变动原因的变量，也称自变量，回归元。

被解释变量:表示分析研究的对象，变动结果的变量，也成应变量。

内生变量:其数值由模型所决定的变量，是模型求解的结果。

外生变量:其数值由模型意外决定的变量。

外生变量数值的变化能够影响内生变量的变化，而内生变量却不能反过来影响外生变量。

前定内生变量：过去时期的、滞后的或更大范围的内生变量，不受本模型研究范围的内生变量的影响，但能够影响我们所研究的本期的内生变量。

前定变量：前定内生变量和外生变量的总称。

数据:时间序列数据：按照时间先后排列的统计数据。

截面数据：发生在同一时间截面上的调查数据。

面板数据：虚拟变量数据：表征政策，条件等，一般取0或1.4、估计评价统计性质的标准无偏：E（＾β）=β 随机变量，变量的函数？有效：最小方差性一致：N趋近无穷时，β估计越来越接近真实值5、检验经济意义检验：所估计的模型与经济理论是否相等统计推断检验：检验参数估计值是否抽样的偶然结果，是否显著计量经济检验：是否符合计量经济方法的基本假定预测检验：将模型预测的结果与经济运行的实际对比CH2 CH3 线性回归模型模型（假设）——估计参数——检验——拟合优度——预测1、模型（线性）（1）关于参数的线性 模型就变量而言是线性的；模型就参数而言是线性的。

Y i =β1+β2lnX i +u i线性影响 随机影响Y i =E （Y i |X i ）+u i E （Y i |X i ）=f(X i )=β1+β2lnX i引入随机扰动项，（3）古典假设A 零均值假定 E （u i |X i ）=0B 同方差假定 Var(u i |X i )=E(u i 2)=σ2C 无自相关假定 Cov(u i ,u j )=0D 随机扰动项与解释变量不相关假定 Cov(u i ,X i )=0E 正态性假定u i ~N(0,σ2)F 无多重共线性假定Rank(X)=k2、估计在古典假设下，经典框架，可以使用OLS方法：OLS 寻找min ∑e i2 ＾β1ols = (Y 均值)-＾β2(X 均值)＾β2ols = ∑x i y i /∑x i 23、性质OLS 回归线性质（数值性质）（1）回归线通过样本均值 （X 均值,Y 均值）（2）估计值＾Y i 的均值等于实际值Y i 的均值（3）剩余项e i 的均值为0（4）被解释变量估计值＾Y i 与剩余项e i 不相关 Cov(＾Y i ,e i )=0（5）解释变量X i 与剩余项e i 不相关 Cov(e i ,X i )=0在古典假设下，OLS 的统计性质是BLUE 统计 最佳线性无偏估计4、检验(1)Z 检验Ho:β2=0 原假设 验证β2是否显著不为0标准化： Z=（＾β2-β2）/SE （＾β2）~N （0,1） 在方差已知，样本充分大用Z 检验拒绝域在两侧，跟临界值判断，是否β2显著不为0(2)t 检验——回归系数的假设性检验方差未知，用方差估计量代替 ＾σ2=∑e i 2/(n-k) 重点记忆t =（＾β2-β2）/＾SE （＾β2）~t （n-2）拒绝域：|t|>=t 2/a (n-2)拒绝，认为对应解释变量对被解释变量有显著影响。

第七章 案例分析【案例7.1】 为了研究1955—1974年期间美国制造业库存量Y 和销售额X 的关系，我们在例7.3中采用了经验加权法估计分布滞后模型。

尽管经验加权法具有一些优点，但是设置权数的主观随意性较大，要求分析者对实际问题的特征有比较透彻的了解。

下面用阿尔蒙法估计如下有限分布滞后模型：tt t t t t u X X X X Y +++++=---3322110ββββα将系数i β(i =0,1,2,3)用二次多项式近似，即00αβ=2101αααβ++=210242αααβ++= 210393αααβ++=则原模型可变为t t t t t u Z Z Z Y ++++=221100αααα其中3212321132109432---------++=++=+++=t t t t t t t t t t t t t X X X Z X X X Z X X X X Z在Eviews 工作文件中输入X 和Y 的数据，在工作文件窗口中点击“Genr ”工具栏，出现对话框，输入生成变量Z 0t 的公式，点击“OK ”；类似，可生成Z 1t 、Z 2t 变量的数据。

进入Equation Specification 对话栏，键入回归方程形式Y C Z0 Z1 Z2点击“OK ”，显示回归结果（见表7.2）。

表7.2表中Z0、 Z1、Z2对应的系数分别为210ααα、、的估计值210ˆˆˆααα、、。

将它们代入分布滞后系数的阿尔蒙多项式中，可计算出3210ˆˆˆˆββββ、、、的估计值为： -0.522)432155.0(9902049.03661248.0ˆ9ˆ3ˆˆ0.736725)432155.0(4902049.02661248.0ˆ4ˆ2ˆˆ 1.131142)432155.0(902049.0661248.0ˆˆˆˆ661248.0ˆˆ21012101210100=-⨯+⨯+=++==-⨯+⨯+=++==-++=++===αααβαααβαααβαβ从而，分布滞后模型的最终估计式为：32155495.076178.015686.1630281.0419601.6----+++-=t t t t t X X X X Y在实际应用中，Eviews 提供了多项式分布滞后指令“PDL ”用于估计分布滞后模型。

《计量经济学》各章重点知识总结整理笔记第二章1、变量间的关系分为函数关系与相关关系。

相关系数是对变量间线性相关程度的度量。

2、现代意义的回归是一个被解释变量对若干个解释变量依存关系的研究，回归的实质是由固定的解释变量去估计被解释变量的平均值。

简单线性回归模型是只有一个解释变量的线性回归模型。

3、总体回归函数（PRF ）是将总体被解释变量Y 的条件均值()i i E Y X 表现为解释变量X 的某种函数。

样本回归函数（SRF ）是将被解释变量Y 的样本条件均值^i Y 表示为解释变量X 的某种函数。

总体回归函数与样本回归函数的区别与联系。

4、随机扰动项i u 是被解释变量实际值i Y 与条件均值()i i E Y X的偏差，代表排除在模型以外的所有因素对Y 的影响。

5、简单线性回归的基本假定：对模型和变量的假定、对随机扰动项u 的假定（零均值假定、同方差假定、无自相关假定、随机扰动与解释变量不相关假定、正态性假定）6、普通最小二乘法（OLS ）估计参数的基本思想及估计式；OLS 估计式的分布性质及期望、方差和标准误差；OLS 估计式是最佳线性无偏估计式。

7、对回归系数区间估计的思想和方法。

8、拟合优度是样本回归线对样本观测数据拟合的优劣程度，可决系数是在总变差分解基础上确定的。

可决系数的计算方法、特点与作用。

9、对回归系数假设检验的基本思想。

对回归系数t 检验的思想与方法；用P 值判断参数的显著性。

10、被解释变量平均值预测与个别值预测的关系，被解释变量平均值的点预测和区间预测的方法，被解释变量个别值区间预测的方法。

11、运用EViews 软件实现对简单线性回归模型的估计和检验。

第二章主要公式表第三章1、多元线性回归模型是将总体回归函数描述为一个被解释变量与多个解释变量之间线性关系的模型。

通常多元线性回归模型可以用矩阵形式表示。

2、多元线性回归模型中对随机扰动项u的假定，除了零均值假定、同方差假定、无自相关假定、随机扰动与解释变量不相关假定、正态性假定以外，还要求满足无多重共线性假定。

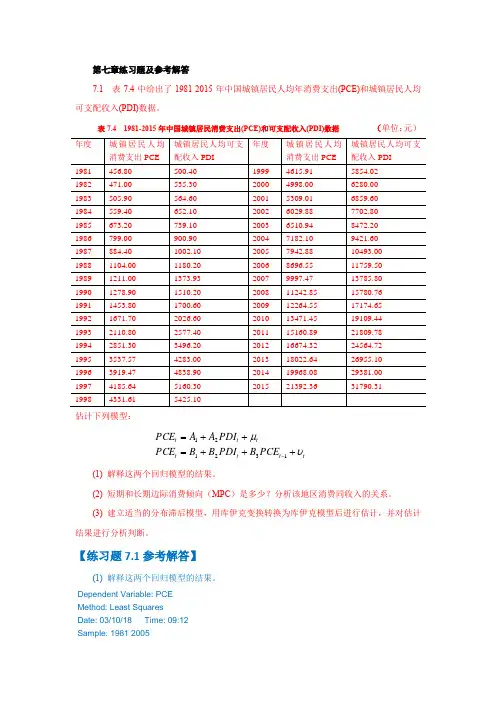
第七章练习题及参考解答7.1 表7.4中给出了1981-2015年中国城镇居民人均年消费支出(PCE)和城镇居民人均可支配收入(PDI)数据。

表7.4 1981-2015年中国城镇居民消费支出(PCE)和可支配收入(PDI)数据 （单位：元）估计下列模型：tt t t tt t PCE B PDI B B PCE PDI A A PCE υμ+++=++=-132121(1) 解释这两个回归模型的结果。

(2) 短期和长期边际消费倾向（MPC ）是多少？分析该地区消费同收入的关系。

(3) 建立适当的分布滞后模型，用库伊克变换转换为库伊克模型后进行估计，并对估计结果进行分析判断。

【练习题7.1参考解答】(1) 解释这两个回归模型的结果。

Dependent Variable: PCE Method: Least Squares Date: 03/10/18 Time: 09:12 Sample: 1981 2005Variable Coefficient Std. Error t-Statistic Prob.C 149.0975 24.56734 6.068933 0.0000R-squared 0.998965 Mean dependent var 2983.768Adjusted R-squared 0.998920 S.D. dependent var 2364.412S.E. of regression 77.70773 Akaike info criterion 11.62040Sum squared resid 138885.3 Schwarz criterion 11.71791Log likelihood -143.2551 F-statistic 22196.24Durbin-Watson stat 0.531721 Prob(F-statistic) 0.000000收入跟消费间有显著关系。

空间滞后模型和空间自回归模型空间滞后模型（Spatial Lag Model）和空间自回归模型（Spatial Autoregressive Model）是空间计量经济学中常用的两种模型，用于分析空间数据中的空间依赖性。

空间滞后模型是一种描述因变量与其邻近地区的自变量之间的依赖关系的模型。

它假设一个地区的因变量取决于该地区的自身特征以及其邻近地区的特征。

换句话说，该模型认为一个地区的因变量受到其邻近地区因变量的影响。

空间滞后模型可以用以下公式表示：Y = ρWy + Xβ + ε。

其中，Y是因变量，Wy是空间权重矩阵，ρ是空间滞后参数，X是自变量矩阵，β是自变量系数，ε是误差项。

空间滞后模型考虑了空间上的依赖性，可以用来解释因变量的空间聚集现象。

空间自回归模型是一种描述因变量与其邻近地区的因变量之间的依赖关系的模型。

它假设一个地区的因变量取决于该地区的自身特征以及其邻近地区的因变量。

换句话说，该模型认为一个地区的因变量受到其邻近地区因变量的影响。

空间自回归模型可以用以下公式表示：Y = ρWY + Xβ +ε。

其中，Y是因变量，W是空间权重矩阵，ρ是空间自回归参数，X是自变量矩阵，β是自变量系数，ε是误差项。

空间自回归模型考虑了空间上的依赖性，可以用来解释因变量的空间自相关现象。

这两种模型都考虑了空间上的依赖性，但是它们的依赖关系不同。

空间滞后模型是因变量与邻近地区的自变量之间的依赖关系，而空间自回归模型是因变量与邻近地区的因变量之间的依赖关系。

在实际应用中，选择使用哪种模型取决于具体问题和数据的特征。

总结起来，空间滞后模型和空间自回归模型是两种常用的空间计量经济学模型，用于分析空间数据中的空间依赖性。

它们都考虑了因变量与邻近地区之间的依赖关系，但是依赖关系的对象不同，一个是自变量，一个是因变量。

第七章练习题及参考解答表中给出了1981-2015年中国城镇居民人均年消费支出(PCE)和城镇居民人均可支配收入(PDI)数据。

表 1981-2015年中国城镇居民消费支出(PCE)和可支配收入(PDI)数据（单位：元）估计下列模型：(1) 解释这两个回归模型的结果。

(2) 短期和长期边际消费倾向（MPC）是多少分析该地区消费同收入的关系。

(3) 建立适当的分布滞后模型，用库伊克变换转换为库伊克模型后进行估计，并对估计结果进行分析判断。

【练习题参考解答】(1) 解释这两个回归模型的结果。

Dependent Variable: PCEMethod: Least SquaresDate: 03/10/18 Time: 09:12Sample: 1981 2005Included observations: 25Variable CoefficientStd.Errort-StatisticProb.CPDIR-squared Mean dependentvarAdjusted R-squared . dependent var. of regression Akaike infocriterionSum squared resid Schwarz criterionLog likelihood F-statisticDurbin-Watsonstat Prob(F-statistic)收入跟消费间有显着关系。

收入每增加1元，消费增加元。

Dependent Variable: PCEMethod: Least SquaresDate: 03/10/18 Time: 09:13Sample(adjusted): 1982 2005Included observations: 24 after adjusting endpointsVariable CoefficientStd.Errort-StatisticProb.C PDIPCE(-1)R-squared Mean dependentvarAdjusted R-squared . dependent var. of regression Akaike infocriterionSum squared resid Schwarz criterionLog likelihood F-statisticDurbin-Watsonstat Prob(F-statistic)(2) 短期和长期边际消费倾向（MPC）是多少分析该地区消费同收入的关系。

《计量经济学》实验报告实验课题：各章节案列分析姓名：茆汉成班级：会计学12-2班学号： **********指导老师：***报告日期： 2015.06.18目录第二章简单线性回归模型案例 (1)1 问题引入 (1)2 模型设定 (1)3 估计参数 (3)4 模型检验 (3)第三章多元线性回归模型案例 (5)1 问题引入 (5)2 模型设定 (5)3 估计参数 (6)4 模型检验 (6)第四章多重线性案例 (8)1 问题引入 (8)2 模型设定 (8)3 参数估计 (8)4 对多重共线性的处理 (9)第五章异方差性案例 (11)1 问题引入 (11)2 模型设定 (11)3 参数估计 (11)4 异方差检验 (12)5 异方差性的修正 (14)第六章自相关案例 (15)1 问题引入 (15)2 模型设定 (15)3 用OLS估计 (15)4 自相关其他检验 (16)5 消除自相关 (17)第七章分布滞后模型与自回归模型案例 (19)7.2案例1 (19)1 问题引入 (19)2 模型设定 (19)3 参数估计 (19)7.3案例2 (21)1 问题引入 (21)2 模型设定 (21)3、回归分析 (21)4 模型检验 (23)第八章虚拟变量回归案例 (24)1 问题引入 (24)2 模型设定 (24)3 参数估计 (26)4 模型检验 (27)第二章简单线性回归模型案例1、问题引入居民消费在社会经济的持续发展中有着重要的作用。

适度的居民消费规模和合理的消费模型是人民生活水平的具体体现，有利于经济持续健康的增长。

随着社会信息化程度和居民的收入水平的提高，计算机的运用越来越普及，作为居民耐用消费品重要代表的计算机已经为众多的城镇居民家庭所拥有。

研究中国各地区城镇居民计算机拥有量与居民收入水平的数量关系。

影响居民计算机拥有量的因素有多种，但从理论和经验分析，最主要的影响因素应是居民收入水平。

从理论上说居民收入水平越高，居民计算机拥有量越多。

第七章一、单选题1、分布滞后模型：μβββαtt st tt XXXY +++++=--611的滞后长度为（ A ）A 、6，B 、7，C 、8，D 、9；2、下列各项中，不是经验加权法的优点的是（ D ）A 、简单易行，B 、少损失自由度，C 、避免多重共线性，D 、主观随意性大； 3、下列各项不属于库伊克变换的优点的是（B ）A 、使模型结构得到极大简化，B 、具有经济理论依据，C 、最大限度地保证了自由度，D 、很大程度上缓解了多重共线性； 4、下列有关库伊克变换的说法,其中不正确的是:( D )A 、假定滞后解释变量X i t -对被解释变量Y 的影响随着滞后期i(i=0、1、……)的增加而按几何级数衰减；B 、滞后系数的衰减服从某种公比小于1的几何级数；C 、滞后模型的各参数假定满足：λββi i 0=)210,10( 、、、=<<i λ；D 、λ值的大小决定了滞后衰减的速度，λ值越接近0衰减速度越慢。

5、自适应预期假定的其数学表达式为)(*1*1*XX X X t t t t ---+=γ，有关其说法不正确的是：（ A ） A 、该表达式可改写为X X X t t t*1*)1(--+=γγ，表明本期预期值是前一期预期值和本期实际值的加权平均，权数分别为γ和1-γ； B 、如果γ等于0，说明本期实际值忽略，预期没有进行修正； C 、在一般情况下，10<<γ；D 、如果γ等于1，则以本期实际值为预期值，本期预期与前一期预期无关。

6、无限分布滞后模型经库伊克变换后，变成一个一阶自回归模型。

则原模型的随机扰动项u t 与新的库伊克模型的随机扰动项u t *关系是（ A ）A 、u t *=u u t t 1--λ， B 、 u t*=uu t t1)1(---γ，C 、u t *=u t δ， D 、u t*=uu t t 1--7、自适应预期模型中随机扰动项u t *与原模型中随机扰动项u t 的关系是（ B ）A 、u t *=u u t t 1--λ， B 、u t*=uu t t 1)1(---γ，C 、u t *=u t δ， D 、u t*=uu t t 1--8、局部调整模型中随机扰动项u t *与原模型中随机扰动项u t 的关系是（ C ）A 、u t *=u u t t 1--λ， B 、 u t*=uu t t 1)1(---γ，C 、u t *=u t δ， D 、 u t*=uu t t 1--9、假定原模型的随机扰动项u t 满足古典假定，则由其转化而来的库伊克模型的Cov(u t *,)*1u t -=（ B ）A 、σλ2， B 、σλ2-， C 、σλ21-， D 、010、使经济变量产生滞后现象的原因众多，下列那一项除外（ D ）： A 、心理预期因素， B 、技术因素， C 、制度因素， D 、测量误差； 11、下列不属于库伊克变换缺陷的是|（ A ）： A 、滞后长度难以确定，B 、新模型的随机扰动项存在一阶自相关，C 、将随机变量Y 1-t 作为解释变量引入了模型，不一定符合基本假定。

自回归分布滞后模型自回归分布滞后模型（ARIMA）是一种可用于自回归过程的统计建模技术。

它的主要优点是它能够使用时间序列数据预测未来或者检测和调整自回归过程中可能存在的性质变化。

ARIMA是一种重要的时间序列分析技术，它可以用来预测变量的自回归过程（AR），如动量（MA）和季节性过程（I）。

一、什么是自回归分布滞后模型（ARIMA）自回归分布滞后模型（ARIMA）是一种用于分析和预测时间序列数据的统计学方法。

ARIMA模型可以帮助研究者分析并预测事件的发生情况，以及由事件的发生情况产生的结果。

ARIMA模型的结构可以被定义为简单的一般线性二阶拟合模型。

二、ARIMA模型的有效性ARIMA模型通常证明是有效预测时间序列数据的一种有效方法。

无论是实现和应用于单变量和多变量时间序列上，ARIMA模型都可以为研究者提供可靠的预测结果。

在单变量的时间序列数据分析中，ARIMA 模型可以帮助研究者发现一些未知的趋势，从而判断该变量在未来的运动趋势。

三、ARIMA模型的应用ARIMA模型的应用，可以分为零度模型和非零度模型应用。

它们可以应用于单变量时间序列（零度模型）和多变量时间序列（非零度模型）上。

零度模型可以用来描述和预测单变量时间序列，而非零度模型可以用来描述和预测多变量时间序列中变量之间的关系。

此外，ARIMA模型还可以应用于时间序列平滑、广义线性模型、转换型自回归等领域。

四、ARIMA模型的优缺点ARIMA模型的优点是它能够有效地描述时间序列的差异性，可以使用时间序列数据预测未来或者检测已经发生的变化，进而找出时间序列中可能存在的自回归过程的特征，从而可以有效的预测和预测时间序列的发展趋势。

缺点是在使用自回归过程时，数据分析人员必须对变量进行较小的调整，以保持变量在ARIMA模型中是稳定的，而如果调整失败，将无法得到良好的分析结果。