参数点估计应用实例

参数估计方法与实例例题和知识点总结一、参数估计的概念参数估计是指根据从总体中抽取的样本估计总体分布中包含的未知参数。

参数通常是描述总体分布的特征值，比如均值、方差、比例等。

二、参数估计的方法（一）点估计点估计就是用样本统计量来估计总体参数，给出一个具体的数值。

常见的点估计方法有矩估计法和最大似然估计法。

1、矩估计法矩估计法的基本思想是用样本矩来估计总体矩。

比如，用样本均值估计总体均值，用样本方差估计总体方差。

2、最大似然估计法最大似然估计法是求使得样本出现的概率最大的参数值。

它基于这样的想法：如果在一次抽样中得到了某个样本，那么这个样本出现概率最大的参数值就是总体参数的估计值。

（二）区间估计区间估计则是给出一个区间，认为总体参数以一定的概率落在这个区间内。

区间估计通常包含置信水平和置信区间两个概念。

置信水平表示区间包含总体参数的可靠程度，常见的置信水平有90%、95%和 99%。

置信区间则是根据样本数据计算得到的一个区间范围。

三、实例例题假设我们要研究某地区成年人的身高情况。

随机抽取了 100 名成年人，他们的身高数据如下（单位：厘米）：165, 170, 172, 168, 175, 180, 160, 178, 176, 169,（一）点估计1、用样本均值估计总体均值：计算这 100 个数据的均值，得到样本均值为 172 厘米。

因此，我们估计该地区成年人的平均身高约为 172 厘米。

2、用样本方差估计总体方差：计算样本方差，得到约为 25 平方厘米。

（二）区间估计假设我们要以 95%的置信水平估计总体均值的置信区间。

首先，根据样本数据计算样本标准差，然后查找标准正态分布表或使用相应的统计软件，得到置信系数。

最终计算出置信区间为（168，176）厘米。

这意味着我们有 95%的把握认为该地区成年人的平均身高在 168 厘米到 176 厘米之间。

四、知识点总结（一）点估计的评价标准1、无偏性：估计量的期望值等于被估计的参数。

多因素敏感性分析法一、多参数敏感性分析多因素敏感性分析，就是对两个以上因素同时发生变动的敏感性分析就称之为多因素敏感性分析。

进行多因素敏感性分析就是考察多个因素同时变化对项目的影响程度，帮助决策者掌握各个因素对指标影响的重要程度，在对各相关因素相互变化进行预测、判断的基础上，对项目的经济效果作进一步的判断，或在实际执行中对敏感因素加以控制，减少项目的风险。

假定其他参数保持不变，仅考察两个参数同时变化对经济效益的影响，称为双因素敏感性分析。

下面以实例说明其应用。

【例5-8】某企业为研究一项投资方案，提供了表5-8所示的参数估计值。

现假定最关键的参数是投资和年收入，试进行双因素敏感性分析。

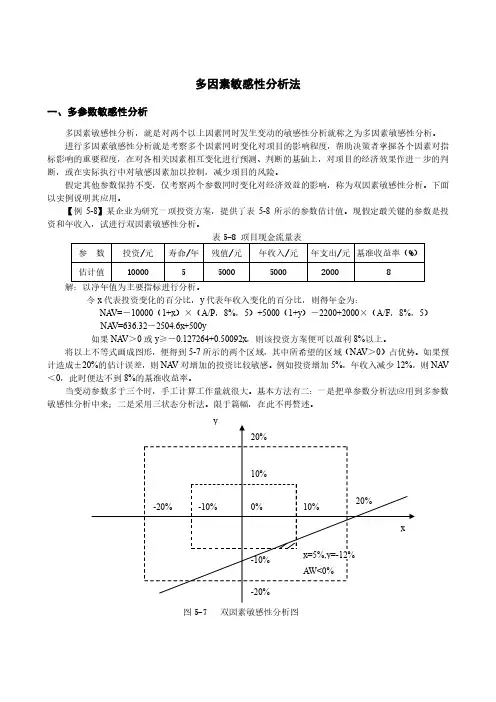
令x 代表投资变化的百分比，y 代表年收入变化的百分比，则得年金为：NA V=－10000（1+x ）×（A/P ，8%，5）+5000（1+y ）－2200+2000×（A/F ，8%，5）NA V=636.32－2504.6x +500y如果NA V ＞0或y ≥－0.127264+0.50092x ，则该投资方案便可以盈利8%以上。

将以上不等式画成图形，便得到5-7所示的两个区域，其中所希望的区域（NA V ＞0）占优势。

如果预计造成±20%的估计误差，则NA V 对增加的投资比较敏感。

例如投资增加5%，年收入减少12%，则NA V ＜0，此时便达不到8%的基准收益率。

当变动参数多于三个时，手工计算工作量就很大。

基本方法有二：一是把单参数分析法应用到多参数敏感性分析中来；二是采用三状态分析法。

限于篇幅，在此不再赘述。

图5-7 双因素敏感性分析图二、敏感性分析的应用要点及局限性敏感性分析能够指明因素变动对项目经济效益的影响，从而有助于理清项目对因素的不利变动所能容许的风险程度，有助于鉴别哪些是敏感因素，从而能够及早放松对那些无足轻重变动因素的注意力，把进一步深入调查研究的重点集中放在那些敏感因素上，或者针对敏感因素制订出管理和应变对策，以达到尽量减少风险、增加决策可靠性的目的。

韦伯分布参数估计引言韦伯分布（Weibull distribution ）是一种常见的概率分布，广泛应用于可靠性工程、生物学、工业工程等领域。

它具有灵活性和适应性强的特点，在数据建模和分析中发挥着重要的作用。

韦伯分布的参数估计是使用已观测到的数据计算韦伯分布的参数，从而对未来的事件进行预测和分析。

韦伯分布的定义韦伯分布是一种连续概率分布，其概率密度函数由下式给出：f (x;λ,k )={(k λ)(x λ)k−1e −(x λ)k,x ≥0;0,x <0.其中，x 是随机变量的取值，λ 是形状参数，k 是尺度参数。

韦伯分布参数估计方法对于韦伯分布的参数估计，常用的方法有最大似然估计法和矩估计法。

1. 最大似然估计法最大似然估计法是一种常用的参数估计方法，其思想是寻找参数值，使得观测到的数据在该参数值下的似然函数取得最大值。

对于韦伯分布，最大似然估计法的步骤如下：1. 建立似然函数。

假设有n 个观测值 x 1,x 2,...,x n ，则似然函数定义为：L (λ,k )=∏[k λ(x i λ)k−1e −(x i /λ)k ]ni=1 2. 对似然函数取对数。

对数似然函数的形式为：lnL (λ,k )=∑[lnk −lnλ+(k −1)ln (x i /λ)−(x i /λ)k ]ni=13.求解对数似然函数的偏导数为零的方程，得到参数的估计值。

对参数λ和k分别求偏导数，并令偏导数为零，可以得到方程组：{∂∂λlnL(λ,k)=∑[kλ2(x iλ)k−1−k(k−1)λ(x iλ)k]ni=1=0∂∂k lnL(λ,k)=∑[1k−ln(x i/λ)k2−ln(x i/λ)+(x iλ)kln(x i/λ)]ni=1=0通过求解以上方程组，可以得到参数λ和k的最大似然估计值。

2. 矩估计法矩估计法是另一种常用的参数估计方法，其基本思想是通过样本矩与理论矩的等值性对参数进行估计。

对于韦伯分布，矩估计法的步骤如下：1.计算样本矩。

概率论与数理统计实验实验3 参数估计假设检验实验目的实验内容直观了解统计描述的基本内容。

2、假设检验1、参数估计3、实例4、作业一、参数估计参数估计问题的一般提法X1, X2,…, Xn要依据该样本对参数作出估计，或估计的某个已知函数.现从该总体抽样，得样本设有一个统计总体，总体的分布函数向量). 为F(x, )，其中为未知参数( 可以是参数估计点估计区间估计点估计——估计未知参数的值区间估计——根据样本构造出适当的区间，使他以一定的概率包含未知参数或未知参数的已知函数的真?（一）、点估计的求法1、矩估计法基本思想是用样本矩估计总体矩.令设总体分布含有个m未知参数??1 ，…，??m解此方程组得其根为分别估计参数??i ，i=1,...,m，并称其为??i 的矩估计。

2、最大似然估计法（二）、区间估计的求法反复抽取容量为n的样本,都可得到一个区间,这个区间可能包含未知参数的真值,也可能不包含未知参数的真值,包含真值的区间占置信区间的意义1、数学期望的置信区间设样本来自正态母体X(1) 方差?? 2已知, ?? 的置信区间(2) 方差?? 2 未知, ?? 的置信区间2、方差的区间估计未知时, 方差?? 2 的置信区间为（三）参数估计的命令1、正态总体的参数估计设总体服从正态分布，则其点估计和区间估计可同时由以下命令获得：[muhat,sigmahat,muci,sigmaci] = normfit(X,alpha)此命令以alpha 为显著性水平，在数据X下，对参数进行估计。

（alpha缺省时设定为0.05），返回值muhat是X的均值的点估计值，sigmahat是标准差的点估计值, muci是均值的区间估计,sigmaci是标准差的区间估计.例1、给出两列参数?? =10, ??=2正态分布随机数，并以此为样本值，给出?? 和?? 的点估计和区间估计命令:r=normrnd(10,2,100,2);[mu,sigm,muci,sigmci]=normfit(r);[mu1,sigm1,muci1,si gmci1]=normfit(r,0.01);mu=9.8437 9.9803sigm=1.91381.9955muci=9.4639 9.584310.2234 10.3762sigmci=1.68031.75202.2232 2.3181mu1=9.8437 9.9803sigm1=1.91381.9955muci1=9.3410 9.456210.3463 10.5043sigmci1=1.6152 1.68412.3349 2.4346例2、产生正态分布随机数作为样本值，计算区间估计的覆盖率。

winno nlin中b i o e q u i v a l e n c e参数一、概述在药物研究与开发领域，判断药物的生物等效性（bi oe qu i va le nc e）是一项重要任务。

Wi n no nl in作为一款专业的药物代谢动力学软件，提供了丰富的功能与参数来进行生物等效性评估。

本文将介绍Wi n no nl in中关于生物等效性参数的详细信息。

二、常用参数C m a x参数1.：Cm ax是指药物在血浆中的最高浓度。

在判断生物等效性中，通常需要比较两个药物在C ma x方面的差异。

在Wi nn on l in中，可以使用“C ma x”参数来计算和分析不同药物的Cm ax值，并进行统计学分析。

A U C参数2.：AU C是指药物在血浆中的面积曲线下面积（a re au nd er th ec ur v e）。

在生物等效性评估中，比较两个药物的A UC值可以获得它们在体内的吸收和消除情况。

W in no nl in提供了多种A UC参数，如AU C0-t、A U C0-i nf等，可以直观地反映不同时间段内药物的曲线下面积。

T m a x参数3.：Tm ax是指药物在血浆中达到最高浓度的时间点。

通过比较两个药物的T max参数，可以了解它们在吸收速度方面的差异。

W i nn on li n中的T ma x参数可以帮助用户确定药物的吸收峰值出现时间，并进行统计学分析。

剂量参数4.：剂量参数是判断药物生物等效性的重要依据之一。

在W i nn on li n中，可以通过设置不同的剂量参数，如剂量比（D os eR at io）、剂量差异（Do se Di ff er e nc e）等来评估不同剂量条件下的药物效果差异。

三、分析方法单剂量法1.：单剂量法常用于比较两个药物在单一剂量条件下的生物等效性。

在W in no nl i n中，选择单剂量法，用户可以通过合适的参数设置和统计学分析得出两种药物之间的生物等效性结论。

§2.5 一元线性回归模型的置信区间与预测多元线性回归模型的置信区间问题包括参数估计量的置信区间和被解释变量预测值的置信区间两个方面，在数理统计学中属于区间估计问题。

所谓区间估计是研究用未知参数的点估计值（从一组样本观测值算得的）作为近似值的精确程度和误差范围，是一个必须回答的重要问题。

一、参数估计量的置信区间在前面的课程中，我们已经知道，线性回归模型的参数估计量^β是随机变量i y 的函数，即：i i y k ∑=1ˆβ，所以它也是随机变量。

在多次重复抽样中，每次的样本观测值不可能完全相同，所以得到的点估计值也不可能相同。

现在我们用参数估计量的一个点估计值近似代表参数值，那么，二者的接近程度如何？以多大的概率达到该接近程度？这就要构造参数的一个区间，以点估计值为中心的一个区间（称为置信区间），该区间以一定的概率（称为置信水平）包含该参数。

即回答1β以何种置信水平位于()a a +-11ˆ,ˆββ之中，以及如何求得a 。

在变量的显著性检验中已经知道)1(~^^---=k n t s t iii βββ (2.5.1)这就是说，如果给定置信水平α-1，从t 分布表中查得自由度为(n-k-1)的临界值2αt ，那么t 值处在()22,ααt t -的概率是α-1。

表示为ααα-=<<-1)(22t t t P即αββαβα-=<-<-1)(2^2^t s t P iiiαββββαβα-=⨯+<<⨯-1)(^^2^2^iis t s t P i i i于是得到：在（α-1）的置信水平下i β的置信区间是)(^^2^2^iis t s t i i βαβαββ⨯+⨯-，i=0,1 （2.5.3）在某例子中，如果给定01.0=α，查表得012.3)13()1(005.02==--t k n t α 从回归计算中得到01.0,15,21.0ˆ,3.102ˆ1ˆˆ10====ββββS S 根据（2.5.2）计算得到10,ββ的置信区间分别为()48.147,12.57和（0.1799,0.2401） 显然，参数1β的置信区间要小。

参数估计和假设检验1. 引言参数估计和假设检验是统计学中两个重要的概念和技术。

它们在数据分析中起着核心的作用，旨在对总体进行推断和判断。

本文将详细介绍参数估计和假设检验的概念、原理、方法和应用。

2. 参数估计参数估计是统计学中对总体未知参数进行估计的过程。

常见的参数估计方法有点估计和区间估计。

2.1 点估计点估计是一种参数估计方法，通过使用样本数据来估计总体参数的值。

常用的点估计方法包括最大似然估计和最小二乘估计。

最大似然估计是指在给定样本条件下，选择使得观测到的样本数据出现概率最大的参数值作为参数的估计值。

最小二乘估计是使用拟合曲线与观测数据之间的差异来估计参数值。

2.2 区间估计区间估计是一种参数估计方法，用于对总体参数进行估计，并提供一个置信区间。

置信区间是指对总体参数的一个范围估计，这个范围通常与给定的置信水平有关。

在进行区间估计时，常常使用样本统计量和抽样分布来计算得到。

3. 假设检验假设检验是一种基于样本数据对总体假设进行检验的方法。

它通过比较样本数据与假设之间的差异来判断总体参数是否满足特定的条件。

假设检验分为单样本假设检验和双样本假设检验两种。

3.1 单样本假设检验单样本假设检验是指在给定样本条件下，对总体参数进行检验。

主要包括均值检验和比例检验两种。

均值检验适用于对总体均值的假设进行检验，常用的方法有t检验和Z检验。

比例检验适用于对总体比例的假设进行检验，常用的方法有卡方检验和Fisher确切检验。

3.2 双样本假设检验双样本假设检验是指在给定两个样本条件下，对两个总体参数之间的差异进行检验。

主要包括独立样本检验和配对样本检验两种。

独立样本检验适用于两个样本是独立的情况下对总体参数之间的差异进行检验，常用的方法有独立双样本t检验和Wilcoxon秩和检验。

配对样本检验适用于两个样本是相关的情况下对总体参数之间的差异进行检验，常用的方法有配对双样本t检验和符号检验。

4. 应用实例参数估计和假设检验在实际数据分析中具有广泛的应用。

点估计与区间估计的基本概念估计是统计学中重要的概念之一，通过样本数据对总体参数进行推断。

在统计推断的过程中，点估计和区间估计是两种常用的方法。

本文将介绍点估计和区间估计的基本概念及其在实际问题中的应用。

一、点估计点估计是根据样本数据，通过一个单一数值来估计总体参数的方法。

该点估计值通常使用样本统计量来表示，例如样本均值、样本方差等。

点估计的目标是选择一个无偏性且有效性较高的估计量。

在点估计中，我们往往考虑以下两个性质：1. 无偏性：估计量的期望值等于总体参数的真实值。

即E(θ̂) = θ，其中θ̂为估计量，θ为总体的真实参数值。

2. 有效性：估计量的方差越小越好，即估计结果越稳定。

一个有效的估计量能够较准确地刻画总体参数的真实情况。

通过点估计，我们可以根据样本数据得到一个具体的数值，对总体参数进行估计。

但是需要注意的是，点估计仅给出了一个估计值，并没有提供参数的误差范围。

为了更全面地推断总体参数，我们引入了区间估计方法。

二、区间估计区间估计是在点估计的基础上，进一步给出参数估计的置信区间。

置信区间是一个区间范围，我们相信总体参数在这个区间内的概率较大。

通常，我们使用样本统计量加减一个适当的值来构建置信区间。

区间估计的过程可以简单分为以下几步：1. 选择置信水平：置信水平反映了我们对置信区间的可信程度。

常用的置信水平有95%和99%。

2. 计算标准误差：标准误差是对总体参数估计的不确定性进行度量的指标。

通过样本数据计算得到。

3. 确定临界值：根据置信水平和自由度确定临界值，以对称分布的情况下，通常使用t分布或正态分布。

4. 构造置信区间：通过样本统计量、标准误差和临界值，计算得到置信区间。

置信区间提供了总体参数的一个范围估计，可以反映参数估计的不确定性。

它告诉我们在一定置信水平下，总体参数落在这个区间内的概率较大。

三、点估计与区间估计的应用点估计和区间估计在实际问题中具有广泛的应用。

下面以一个实例来说明。