第七章线性离散系统的分析与校正

第七章 线性离散系统的分析与校正7-1 试根据定义∑∞=-*=0)()(n nTs e nT e s E确定下列函数的)(s E *和闭合形式的)(z E ：⑴ t t e ωsin )(=；⑵ ))()((1)(c s b s a s s E +++=，b a ≠，c a ≠，c b ≠。

解：Ts e z =；⑴ )()sin()(0z E enT s E n nTs==∑∞=-*ω；1)cos(2)sin(21}{21)(20+-=⎥⎦⎤⎢⎣⎡---=-=-∞=--∑z T z z T e z z e z z j e e e j z E T j T j n nTsjwnT jwnT ωωωω。

⑵ ))()((1))()((1))()((1)(c s c b c a b s b c b a a s a c a b s E +--++--++--=； ∑∑∑∞=--∞=--∞=--*--+--+--=000))((1))((1))((1)(n nTs cnT n nTsbnT n nTs anT e e c b c a e e b c b a e e a c a b s E ； ))()(())()(())()(()(cTbT aT e z c b c a ze z b c b a z e z a c a b z z E ------+---+---=； 记))()((c b c a b a ---=∆，∆-=b a k 1，∆-=ca k 2，∆-=cb k 3；))()(()()()()(3)(2)(12321cTbT aT T c b T c a T b a aT bT cT e z e z e z ze k e k e k z e k e k e k z E ---+-+-+-------+-++-=。

7-2 采样周期为T ，试求下列函数的Z 变换：⑴ n a nT e =)(； ⑵ t e t t e 32)(-=；⑶ 3!31)(t t e =； ⑷ 21)(ss s E +=；⑸ )1(1)(2+-=-s s e s E sT 。

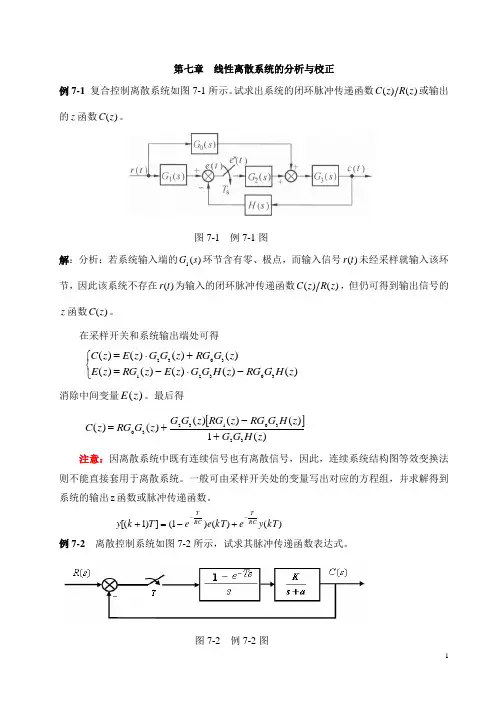
第七章 线性离散系统的分析与校正例7-1 复合控制离散系统如图7-1所示。

试求出系统的闭环脉冲传递函数)()(z R z C 或输出的z 函数)(z C 。

图7-1 例7-1图解：分析：若系统输入端的)(1s G 环节含有零、极点，而输入信号)(t r 未经采样就输入该环节，因此该系统不存在)(t r 为输入的闭环脉冲传递函数)()(z R z C ，但仍可得到输出信号的z函数)(z C 。

在采样开关和系统输出端处可得⎩⎨⎧-⋅-=+⋅=)()()()()()()()()(303213032z H G RG z H G G z E z RG z E z G RG z G G z E z C 消除中间变量)(z E 。

最后得[])(1)()()()()(323013230z H G G z H G RG z RG z G G z G RG z C +-+=注意：因离散系统中既有连续信号也有离散信号，因此，连续系统结构图等效变换法则不能直接套用于离散系统。

一般可由采样开关处的变量写出对应的方程组，并求解得到系统的输出z 函数或脉冲传递函数。

)()()1(])1[(kT y ekT e eT k y RCT RCT --+-=+例7-2 离散控制系统如图7-2所示，试求其脉冲传递函数表达式。

图7-2 例7-2图解：开环脉冲传递函数为 ])([)1(]1[)(1a s s K Z zas K seZ z G Ts+-=+⋅-=--)()1(])(11[)1(1aTaT ez e aK a s a asZ z K -----⋅=+--=闭环脉冲传递函数为aTaTaTeaK aK ez e aKz G z G z ----+--=+=Φ)1()(1)()(例7-3 数字控制系统如图7-3所示，试计算0)(=t r ，)(1)(t t n =，1)(1-=z z K z D 时的稳态输出。

图7-3 例7-3图解：首先要导出以干扰为输入，)(t y 为输出的脉冲传递函数，⎥⎦⎤⎢⎣⎡--+=-)()(1)(11)(z Y z D s e s N s s Y Ts代入ss N 1)(=,上式两端求Z 变换，有)()()1(1)1()1(1)(1z Y z D s s Z z s s Z z Y ⎥⎦⎤⎢⎣⎡+--⎥⎦⎤⎢⎣⎡+=-)()1(1)1(1)1(1)(1z D s s Z z s s Z z Y ⎥⎦⎤⎢⎣⎡+-+⎥⎦⎤⎢⎣⎡+=-而))(1()1()1(1TTe z z ze s s Z -----=⎥⎦⎤⎢⎣⎡+，所以TTe z e s s Z z-----=⎥⎦⎤⎢⎣⎡+-1)1(1)1(1于是 )]()1())[(1()1()(z D e ez z ez z Y TTT----+---=代入1)(1-=z z K z D ，得TTTTez e eK z ez z Y ----++--+-=)]1()1([)1()(12)(z Y 的表达式中，已包含了干扰作用量，采用终值定理计算)(∞Y ，所有的极点必须在单位圆内。