控制工程基础-控制系统的数学模型

第2章系统的数学模型(习题答案)2.1什么是系统的数学模型？常用的数学模型有哪些？解：数学模型就是根据系统运动过程的物理、化学等规律，所写出的描述系统运动规律、特性、输出与输入关系的数学表达式。

常用的数学模型有微分方程、传递函数、状态空间模型等。

2.2 什么是线性系统？其最重要的特性是什么？解：凡是能用线性微分方程描述的系统就是线性系统。

线性系统的一个最重要的特性就是它满足叠加原理。

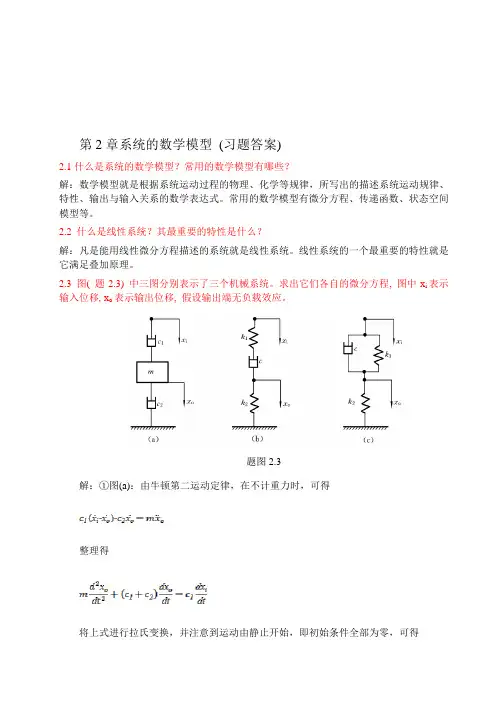
2.3 图( 题2.3) 中三图分别表示了三个机械系统。

求出它们各自的微分方程, 图中x i表示输入位移, x o表示输出位移, 假设输出端无负载效应。

题图2.3解：①图(a)：由牛顿第二运动定律，在不计重力时，可得整理得将上式进行拉氏变换，并注意到运动由静止开始，即初始条件全部为零，可得[]于是传递函数为②图(b)：其上半部弹簧与阻尼器之间，取辅助点A，并设A点位移为x，方向朝下；而在其下半部工。

引出点处取为辅助点B。

则由弹簧力与阻尼力平衡的原则，从A和B两点可以分别列出如下原始方程：消去中间变量x，可得系统微分方程对上式取拉氏变换，并记其初始条件为零，得系统传递函数为③图(c)：以的引出点作为辅助点，根据力的平衡原则，可列出如下原始方程：移项整理得系统微分方程对上式进行拉氏变换，并注意到运动由静止开始，即则系统传递函数为2.4试建立下图（题图2.4）所示各系统的微分方程并说明这些微分方程之间有什么特点，其中电压)(t u r 和位移)(t x r 为输入量；电压)(t u c 和位移)(t x c 为输出量；1,k k 和2k 为弹簧弹性系数；f 为阻尼系数。

+-+-C)(t u r )(t u c )(t r )(t x c f1k 2k CR)(t u r )(u c +-+-f)(t r )(t x c )(a )(b )(c )(d R 2R题图2.4【解】：)(a方法一：设回路电流为i ，根据克希霍夫定律，可写出下列方程组：⎪⎩⎪⎨⎧=+=⎰i R u u dt i C u cc r 1消去中间变量，整理得：dtdu RC u dt du RCrc c =+方法二：dtdu RC u dt du RCRCs RCs CsR R s U s U rc c r c =+⇒+=+=11)()( 由于无质量，各受力点任何时刻均满足∑=0F ，则有：cc r kx dt dxdt dx f =-)(dtdx k f x dt dx k f rc c =+⇒()r r c c r c u dtduC R u dt du C R R Cs R R Cs R Cs R R CsR s U s U +=++⇒+++=+++=221212212)(1111)()( 设阻尼器输入位移为a x ，根据牛顿运动定律，可写出该系统运动方程r rc c aa c a r c r x dtdx k f x dt dx f k k k k dt dx f x x k x x k x x k +=++⇒⎪⎩⎪⎨⎧=--=-22121221)()()( 结论：)(a 、)(b 互为相似系统，)(c 、)(d 互为相似系统。

第二章控制系统的数学模型对于一个控制系统，建立数学模型的目的有二个：第一，模型可以用在现存的控制系统特性的研究中，模型代表了我们对系统特性的认识，并且在我们对系统知道得更多时还可以修改和扩展模型。

第二，在实际系统尚不存在时，例如在建设工程刚刚开始时，可以借助模型来预测设计思想和不同控制策略的效果，而不招致建造和试验系统所带来的费用浪费，也避免了冒危险的可能。

2－1 物理系统的动态描述—数学模型每一个自动控制系统都是由若干个元件组成的。

每个元件在系统中都具有各自的功能，它们相互配合起来就构成一个完整的控制系统，共同实现对某个物理量（被控制量）的控制，而满足所要求的特定规律。

如果把控制系统中各物理量（变量）之间的关系用数学表达式描述出来，就得到了此控制系统的数学模型。

在静态条件下（即变量的各阶导数为零），描述各变量之间关系的数学方程，称为静态模型，而各变量在动态过程中的数学方程，称为动态模型。

在自动控制系统的分析中，主要是研究动态模型。

微分方程中，各变量的导数表示了它们随时间变化的特性。

因此，微分方程完全可以描绘系统的动态特性，微分方程是物理系统数学模型中最基本的一种。

系统的数学模型可以用实验法和分析法建立。

应当指出：同一个控制系统的数学模型可以有许多不同的形式，另外，对于一个具体系统而言，为了在系统分析中，既不包罗万象，把系统数学模型搞得很复杂，又不要忽略主要因素，而失去系统的准确性，必须对系统有全面的、透彻的了解。

得到控制系统的一个既简化又准确的数学模型，这是我们的根本出发点。

2－2 建立系统数学模型的一般步骤由于控制系统是由各种功能不同的元件组成的，因此，要正确建立系统的运动方程式，首先必须研究系统中各个元件的运动方程式，以及这些元件在控制系统中相互联系时的彼此影响等问题。

应当指出，在列写系统和各元件的运动方程式时，往往将系统分成若干个环节，能使问题简化。

所谓环节，就是指可以组成独立的运动方程式的那一部分。

机械控制⼯程基础第⼆章系统的数学模型基本要求、重点和难点⼀、基本要求（1）了解数学模型的基本概念。

能够运⽤动⼒学、电学及专业知识，列写机械系统、电⼦⽹络的微分⽅程。

（2）掌握传递函数的概念、特点，会求传递函数的零点、极点及放⼤系数。

（3）能够⽤分析法求系统的传递函数。

（4）掌握各个典型环节的特点，传递函数的基本形式及相关参数的物理意义。

（5）了解传递函数⽅框图的组成及意义；能够根据系统微分⽅程，绘制系统传递函数⽅框图，并实现简化，从⽽求出系统传递函数。

（6）掌握闭环系统中前向通道传递函数、开环传递函数、闭环传递函数的定义及求法。

掌握⼲扰作⽤下，系统的输出及传递函数的求法和特点。

（7）了解相似原理的概念。

（8）了解系统的状态空间表⽰法，了解MATLAB中，数学模型的⼏种表⽰法。

⼆、本章重点（1）系统微分⽅程的列写。

（2）传递函数的概念、特点及求法；典型环节的传递函数。

（3）传递函数⽅框图的绘制及简化。

三、本章难点（1）系统微分⽅程的列写。

（2）传递函数⽅框图的绘制及简化。

概述系统按其微分⽅程是否线性这⼀特性，可以分为线性系统和⾮线性系统。

如果系统的运动状态能⽤线性微分⽅程表⽰，则此系统为线性系统。

线性系统的⼀个最重要的特性就是满⾜叠加原理。

线性系统⼜可分为线性定常系统和线性时变系统。

系统的数学模型是系统动态特性的数学描述。

对于同⼀系统，数学模型可以有多种形式，如微分⽅程、传递函数、单位脉冲响应函数及频率特性等等。

但系统是否线性这⼀特性，不会随模型形式的不同⽽改变。

线性与⾮线性是系统的固有特性，完全由系统的结构与参数确定。

系统建模是经典控制理论和现代控制理论的基础。

建⽴系统数学模型的⽅法有分析法和实验辨识法两种。

前者主要⽤于对系统结构及参数的认识都⽐较清楚的简单系统，⽽后者通常⽤于对系统结构和参数有所了解，⽽需进⼀步精化系统模型的情况。

对于复杂系统的建模往往是⼀个分析法与实验辨识法相结合的多次反复的过程。

第2章系统的数学模型(习题答案)2.1什么是系统的数学模型？常用的数学模型有哪些？解：数学模型就是根据系统运动过程的物理、化学等规律，所写出的描述系统运动规律、特性、输出与输入关系的数学表达式。

常用的数学模型有微分方程、传递函数、状态空间模型等。

2.2 什么是线性系统？其最重要的特性是什么？解：凡是能用线性微分方程描述的系统就是线性系统。

线性系统的一个最重要的特性就是它满足叠加原理。

2.3 图( 题2.3) 中三图分别表示了三个机械系统。

求出它们各自的微分方程, 图中x i表示输入位移, x o表示输出位移, 假设输出端无负载效应。

题图2.3解：①图(a)：由牛顿第二运动定律，在不计重力时，可得整理得将上式进行拉氏变换，并注意到运动由静止开始，即初始条件全部为零，可得[]于是传递函数为②图(b)：其上半部弹簧与阻尼器之间，取辅助点A，并设A点位移为x，方向朝下；而在其下半部工。

引出点处取为辅助点B。

则由弹簧力与阻尼力平衡的原则，从A和B两点可以分别列出如下原始方程：消去中间变量x，可得系统微分方程对上式取拉氏变换，并记其初始条件为零，得系统传递函数为③图(c)：以的引出点作为辅助点，根据力的平衡原则，可列出如下原始方程：移项整理得系统微分方程对上式进行拉氏变换，并注意到运动由静止开始，即则系统传递函数为2.4试建立下图（题图2.4）所示各系统的微分方程并说明这些微分方程之间有什么特点，其中电压)(t u r 和位移)(t x r 为输入量；电压)(t u c 和位移)(t x c 为输出量；1,k k 和2k 为弹簧弹性系数；f 为阻尼系数。

+-+-C)(t u r )(t u c )(t r )(t x c f1k 2k CR)(t u r )(u c +-+-f)(t r )(t x c )(a )(b )(c )(d R 2R题图2.4【解】：)(a方法一：设回路电流为i ，根据克希霍夫定律，可写出下列方程组：⎪⎩⎪⎨⎧=+=⎰i R u u dt i C u cc r 1消去中间变量，整理得：dtdu RC u dt du RCrc c =+方法二：dtdu RC u dt du RCRCs RCs CsR R s U s U rc c r c =+⇒+=+=11)()( 由于无质量，各受力点任何时刻均满足∑=0F ，则有：cc r kx dt dxdt dx f =-)(dtdx k f x dt dx k f rc c =+⇒()r r c c r c u dtduC R u dt du C R R Cs R R Cs R Cs R R CsR s U s U +=++⇒+++=+++=221212212)(1111)()( 设阻尼器输入位移为a x ，根据牛顿运动定律，可写出该系统运动方程r rc c aa c a r c r x dtdx k f x dt dx f k k k k dt dx f x x k x x k x x k +=++⇒⎪⎩⎪⎨⎧=--=-22121221)()()( 结论：)(a 、)(b 互为相似系统，)(c 、)(d 互为相似系统。