螺纹连接受力分析

钢拉杆三角形和梯形螺纹螺牙受力分析摘要:在目前的工业生产中，钢拉杆螺纹牙根应力的分析计算基于机械设计手册中的悬臂梁理论和假设的方法计算，计算结果与实际应力情况有较大的差距，本文通过对钢拉杆螺纹牙根部受力进行了有限元分析，探究其失效机理。

关键词: 钢拉杆; 螺纹牙根; 有限元分析1 存在的问题目前，螺纹连接可以采用普通螺纹、梯形、矩形、锯齿形等四种形式，其中普通螺纹使用较为普遍，在工业生产中计算钢拉杆螺纹牙型强度时通常采用国内传统螺纹强度计算方法（机械设计手册）。

校核方法为：把螺纹牙展成一根悬臂梁的形式，见下图1，其中设轴向应力为F ，相旋合螺纹圈数为 z ，图 1：螺纹牙受力图剪切强度条件 τ=Fzdb π ≤ [τ]弯曲强度条件 b σ =MW≤[]b σ式中 M =2[]2d d F z -, W = 216d b π由此可得 b σ =2213()F d d d b zπ- ≤[]b σ式中: [τ]为许用切应力/MPa; []b σ 为许用弯曲应力/MPa 。

钱学毅[3]通过对螺纹牙（Tr48×12—8、Tr44×12—8和B40×7等）的有限元受力分析对理论计算方法提出3个问题: (1)从模型上看, 将螺旋形状的螺纹牙力学模型简化成长度远大于横截面尺寸的悬臂梁模型与实际情况差别较大,由此而导出的弯曲强度条件与实际情况差别较大;(2)展开成悬臂梁的力学模型应力的分布规律较之实际的螺旋形模型也不相同;(3)没有考虑剪切对弯曲正应力的影响。

事实上, 螺纹牙根是处于非杆件复杂应力状态,不应该再用材料力学的理论进行分析计算。

而应该运用弹性理论进行分析计算, 取等效正应力作为弯曲强度计算的依据, 而不应该仅考虑由弯矩引起的正应力。

钱学毅等人的研究是相对于较小的螺纹螺牙进行的，然而在实际中还经常用到较大螺纹牙的钢拉杆进行工业生产。

粗牙（较大螺纹牙）和细牙（小螺纹牙 ）的区别：螺距大小不同，粗牙螺距大，细牙小；粗牙螺纹抗疲劳能力强一些，对经常拆装方便一些；细牙自锁能力强，底径尺寸大，静载能力强。

螺纹联接原理
四、硬联接与软联接
扭矩
N.m
< 30 度
硬联接
< 30 度 (ISO 5393)
0
扭矩
N.m
贴合点
> 720 度
角度
软联接
> 720 度 (ISO 5393)
0
贴合点
角度
螺纹联接原理
硬联接与软联接
扭矩
过扭
目标
硬联接
软联接
均值偏差
贴合点 0
角度
螺纹联接原理
硬联接与软联接
动态测试 ：装配的同时用在线式扭矩传感器测量
装配时预紧力的大小通常是通过拧紧力矩来控制的
螺纹联接原理
螺纹的受力分析
螺旋副中的受力情况
拧紧力矩T
摩擦力
预紧力
这是我们需 要控制的！
夹紧力
夹紧力
预紧力
摩擦力
螺纹联接原理
螺纹的受力分析
预紧力和拧紧力矩之间的关系
拧紧力矩T
T T1 T2
螺母端面和支承面之 间的摩擦阻力矩T1

d2 2
QP tg (
力矩紧固及管理方法
螺纹联接原理 工具简介 AF1力矩管理体系
一、螺纹的基本知识
螺纹联接：利用螺纹零件构成可拆式联接
使用联接是为了便于机器的制造、安装、运输、维修以及提高劳动生 产率，常见的可拆式联接有螺纹联接、键联接及销联接等
√ 螺栓联接
√ 螺钉联接
双头螺柱联接
紧定螺钉联接
螺纹联接原理
螺纹的基本知识
（6）螺纹升角ψ ：中径d2圆柱上，螺旋线的切 线与垂直于螺纹轴线的平面的夹角。 （7）牙型角α ：轴向截面内螺纹牙型相邻两侧 边的夹角。牙型侧边与螺纹轴线的垂线间的夹 角。 （8）接触高度 h ：内外螺纹旋合后，接触面的 径向高度。

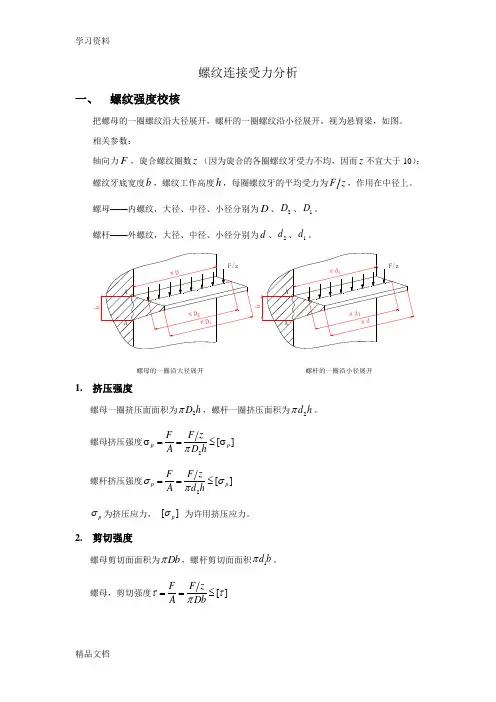
螺纹连接受力分析一、 螺纹强度校核把螺母的一圈螺纹沿大径展开，螺杆的一圈螺纹沿小径展开，视为悬臂梁，如图。

相关参数：轴向力F ，旋合螺纹圈数z （因为旋合的各圈螺纹牙受力不均，因而z 不宜大于10）； 螺纹牙底宽度b ，螺纹工作高度h ，每圈螺纹牙的平均受力为F z ，作用在中径上。

螺母——内螺纹，大径、中径、小径分别为D 、2D 、1D 。

螺杆——外螺纹，大径、中径、小径分别为d 、2d 、1d 。

螺母的一圈沿大径展开螺杆的一圈沿小径展开1. 挤压强度螺母一圈挤压面面积为2D h π，螺杆一圈挤压面积为2d h π。

螺母挤压强度2[]p p F F z A D h πσ==≤σ 螺杆挤压强度2[]p p F F z A d hσσπ==≤ p σ为挤压应力， []p σ 为许用挤压应力。

2. 剪切强度螺母剪切面面积为Db π，螺杆剪切面面积1d b π。

螺母，剪切强度[]F F z A Dbττπ==≤螺杆，剪切强度1[]F F z A d bττπ==≤ []0.6[]τσ=，[]snσσ=为材料许用拉应力，s σ为材料屈服应力。

安全系数，一般取3～5。

3. 弯曲强度危险截面螺纹牙根部，A-A 。

螺母，弯曲强度23[]b b M Fh W Db zσσπ==≤ 螺杆，弯曲强度213[]b b M Fh W d b zσσπ==≤ 其中，L ：弯曲力臂，螺母22D D L -=，螺杆22d d L -= M ：弯矩，螺母22D D F M F L z -=⋅=⋅，螺杆22d d F M F L z -=⋅=⋅ W ：抗弯模量，螺母26Db W π=，螺杆216d b W π=[]b σ：螺纹牙的许用弯曲应力，对钢材，[]1~1.2[]b σσ=4. 自锁性能自锁条件v ψψ≤， 其中，螺旋升角22arctanarctan S np d d ψππ==，螺距、导程、线数之间关系：S =np ； 当量摩擦角arctan arctancos v v ff ψβ==， 当量摩擦系数cos v f f β=f 为螺旋副的滑动摩擦系数，无量纲，定期润滑条件下，可取0.13～0.17；β为牙侧角，为牙型角α的一半，2βα=5. 螺杆强度1、 实心螺杆[]21F F =A d 4σσπ=≤ 2、 空心按实际情况计算 3、 普通螺纹[]22c 1F F F =A H d d -446σσππ==≤⎛⎫⎪⎝⎭c d ：普通螺纹螺栓拉断截面，是一个经验值，其经验计算公式为c 1Hd d 6=-其中，[]σ为材料的许用拉应力，[]snσσ=，s σ为屈服应力，为安全系数，一般取3～5。

—
ｌ３ －
４
式中 Ｆ 为预 紧力 （ ） Ｎ ， 为螺栓的直径 （一 ） 为螺栓 的许用应力 ｄ ｒ ， ｒ
（ ／ ｍ 。 Ｎｒ ） ａ
此公式可理解 为 ：螺栓被拧 紧时既受 托又受 扭 ，采用第 四强度理 论 ，拉扭合 成 的结果相 当于纯拉伸 的 １ 倍 。应深 刻理解 １ 的物理 意 ． ３ ． ３ 义 ， 安全系数 和可 靠系数等 。 绝非 ２ ． ２既受预 紧力又受 工作载荷 的受拉 螺栓 外载荷为轴 向载荷 Ｆ 或 翻倒 力矩 Ｍ作用 ， 而采用受 拉螺栓 的情况 属于此种情况 ， 度条 件为 ： １ ， 强 ． ３
的相对 刚度系数 ；工作 载荷 Ｆ 由轴 向力 Ｆ 或 翻倒 力矩 Ｍ引起 的 ， 是 。 其 值可 由螺栓组受力分 析相关公式求得 。 如螺 栓受变载荷作 用 ，除按上 述公式进 行设计 或校核 满足静 强度 外 ， 验算螺栓的应力 幅 ， 盯≤【 详 细内容请参 考机械 设计教材 。 尚需 即 叮， ２ ． ３受剪螺栓连接 的强 度设 计 计算 ２． ．１受剪螺栓连 接的强度设计计算 概述 ３ 受剪螺栓 （ 铰制孑 光制螺栓 ） Ｌ 螺栓杆 和螺栓孑采 用基孑 制过渡 配合 Ｌ Ｌ （ ７ ６Ｈ ／６， Ｈ ／ ， ７ ）能精确 固定被 连接件 相对位 置 ， 承受横 向载 荷 ， ｍ ｎ 并能 但 是孔 的加工 精度要求 高 。用于 结构要求 紧凑或连 接空 间受 到 限制 的情 况。受剪螺栓连接 的失效形式 为螺栓 的栓杆部分被 压溃或栓 杆被剪 断。 Ｉ 剪强度计算 ： ） 抗 ２抗压 强度计算 ： ）
横 向力被接缝 面间 的摩 擦力平衡 ，螺栓组受 的转矩 被接缝 面问 的压 力 产 生的摩擦力矩平衡 。拧紧螺栓 时每个螺栓受到 的轴 向拉力 ， 连接件 被 受 到夹紧力 而产生预 紧力 Ｆ。因此螺 栓没有受 到剪切 ，只受到 预紧力 Ｆ， 即只受拉 而不受剪 。 ２螺栓 连接的强度设 汁汁算 及禁忌 螺栓组受力 的分析 目的是 求 出一组 螺栓 中受 力最大 的螺栓 所受 的 力， 进行强度计算 。 作用 于—组螺栓 的外 力有轴 向力 、 横向力 Ｆ 、 转矩 Ｔ及 翻倒 力矩 Ｍ 四种情 况 ， 对于单个 螺栓 的受 力只有 两种情 况 ： 受拉或 受剪 。工程应 用中多数应用 为受拉螺栓 。 ２ ． １只受预 紧力 的受拉螺栓连 接 只受 预 紧力 Ｆ 的受拉 螺栓连 接 ，是指 工作后 不 再受 轴 向载荷作 用 。例如外 载荷为横 向力 Ｆ Ｒ或转矩 Ｔ 用 ， 作 受拉螺 栓连接属 于这种情 况， 只受预 紧力 作用 ， 其强度条件 为 ： １Ｆ， ． ３

5）导程S——同一条螺旋线相邻两牙的轴向距离；
单线：S=t
d2
双线：S=2t
多线：S=nt
n——头数；
右旋

6）升角：螺旋线与水平线夹角；
S t

tg S d2
7）牙型角 牙型斜角
8）牙的工作高度h
S
d2
二、各种螺纹的特点、应用
自锁条件：升角<v（摩擦角）； 牙型斜角越小越不容易加工。
b只受预紧力214dqp???31116dt???紧螺栓联接装配时螺母需要拧紧在拧紧力矩作用下螺栓除受预紧力qp的拉伸而产生拉伸应力外还受螺纹摩擦力矩t1的扭转而产生扭转剪应力使螺栓处于拉伸与扭转的复合应力状态下
第四章 螺纹零件
一、概述
1、作用
联接：起联接作用的螺纹; 传动：起传动作用的螺纹;
2、螺纹的形成 刀具——做直线运动； 工件——做旋转运动； 螺纹线：转动与直线运动；
rz
ks T
z
f ri
i 1
式中：f——结合面的摩擦系数；
ri——第i个螺栓的轴线到螺栓组 对称中心O的距离；
z——螺栓数目；
ks——防滑系数，同前。
机架 地基
T
r4 r1
rr32
Qpf
Qpf
松配
T
r4 r1
rr23
Qpf
Qpf
紧配
b)紧配 当采用紧配螺栓时，在转矩T的作用下，各螺栓受到剪切和挤压
习题： 一、选择题
第四章 螺纹零件
1、在常用的螺旋传动中，传动效率最高的螺纹是 4 。
（1）三角形螺纹；（2）梯形螺纹；（3）锯齿形螺纹；（4）矩 形螺纹；
2、在常用的螺纹联接中，自锁性最好的螺纹是 1 。

螺纹连接受力分析螺纹连接受力分析一、 螺纹强度校核把螺母的一圈螺纹沿大径展开，螺杆的一圈螺纹沿小径展开，视为悬臂梁，如图。

相关参数：轴向力F ，旋合螺纹圈数z （因为旋合的各圈螺纹牙受力不均，因而z 不宜大于10）； 螺纹牙底宽度b ，螺纹工作高度h ，每圈螺纹牙的平均受力为F z ，作用在中径上。

螺母——内螺纹，大径、中径、小径分别为D 、2D 、1D 。

螺杆——外螺纹，大径、中径、小径分别为d 、2d 、1d 。

1. 挤压强度螺母一圈挤压面面积为2D h π，螺杆一圈挤压面积为2d h π。

螺母挤压强度2[]pp F F z A D hπσ==≤σ F/zAπDπD2πD1Ab螺母的一圈沿大径展开F/zAπd1πd2πdAb螺杆的一圈沿小径展开[]b σ：螺纹牙的许用弯曲应力，对钢材，[]1~1.2[]b σσ=2. 自锁性能自锁条件vψψ≤，其中，螺旋升角22arctan arctanSnp d d ψππ==，螺距、导程、线数之间关系：S =np ； 当量摩擦角arctan arctancos vv ff ψβ==， 当量摩擦系数cos v f f β=f为螺旋副的滑动摩擦系数，无量纲，定期润滑条件下，可取0.13～0.17；β为牙侧角，为牙型角α的一半，2βα=3. 螺杆强度1、 实心螺杆[]21FF =A d4σσπ=≤2、 空心 按实际情况计算3、 普通螺纹[]22c 1F F F =A H d d -446σσππ==≤⎛⎫⎪⎝⎭cd ：普通螺纹螺栓拉断截面，是一个经验值，其经验计算公式为c1H dd 6=-其中，[]σ为材料的许用拉应力，[]sn σσ=，sσ为屈服应力，为安全系数，一般取3～5。

二、 螺栓连接强度4. 预紧力计算：一般，螺栓预紧应力可达到材料屈服应力的50%~70%。

T ：预紧力矩，0T K F d =⋅⋅，K 为拧紧力系数，d为螺纹公称直径， 0F ：预紧力，00sFA σ=⋅σ：预紧应力，00.5~0.7sσσ=，sσ为材料屈服应力s A ：螺纹部分危险剖面的面积，24ss Ad π=⋅sd ：螺纹部分危险剖面的计算直径，()23s d d d =+，316dd H =-，5. 松螺栓连接松螺栓连接，工作载荷F ，螺栓危险截面强度[]21FF=A d4σσπ=≤6. 紧螺栓连接紧螺栓连接，无工作载荷时。

F=FQ/z
k f FR 受拉 F s m z
受剪 FS FR / z
受拉 F
kfT
s ri
i 1
Fmax
M rmax
受剪 Fs max
Trmax
r
i 1
z
2
i
r
i 1
z
2
i
单个螺栓 强度计算
Fs [ ] 受剪螺栓： 2 m d 0 /4
螺 纹 联 接
螺纹的分类及相关参数
螺纹要素的相关问题 螺旋副的受力分析
螺纹连接的类型 螺纹连接的相关问题 螺纹连接的强度计算 螺纹连接使用中应注意的问题
§5 螺栓组联接的受力分析
一、思路
联接结构形式、外载荷类型 —→螺栓受力情形 —→找出受载最大螺栓 —→按单个螺栓联接的计算方法计算
二、基本假定
螺纹连接
基本知识
基本理论
螺 纹 类 型 、 特 点 应 用
螺 纹 连 接 类 型 与 应 用
螺 纹 的 拧 紧 与 防 松
主 要 失 效 与 设 计 准 则
单 个 螺 栓 连 接 的 强 度 计 算
螺栓组连接的设计 螺 栓 组 的 结 构 设 计 螺 栓 组 的 受 力 分 析 按 单 个 螺 栓 连 接 的 强 度 计 算
8 105 螺栓由旋转力矩产生的 载荷 FT 400N D 500 Z 8 2 2 T
二. 根据螺栓联接结构，进行 单个螺栓计算
5 4 2 3 1
（1）图a所示，普通螺栓联接： 每个螺栓所受工作载荷的方向如 图所示。经分析，螺栓5所受的 工作载荷最大
F FR F T 500 400 900N

分析得 : F +FQ +Fr=0
ρ =tg-1 f ----摩擦角
F= FQ tan (ψ +)
Fr Fn
v
ρ
f
ψ
F FQ
驱动力矩： T F d2 （螺纹力矩） 2
d2 2
Fatg(
)
F FQ
Fr
对于螺纹连接，T为拧紧螺纹时的螺纹力矩
ψ +ρ
松开时：
相当于使滑块等速沿斜面 下滑，轴向载荷 FQ变为驱 动力， F变为维持滑块等 速运动所需的平衡力。
滑块不能在重力作用下下滑。这一现象称为自锁现 象。螺旋千斤顶就是利用这一原理工作的。
二、非矩形螺纹（=0)
三角形螺纹、梯形螺纹、锯齿形螺纹
1、螺纹受力分析：
轴
=0 线
FQ 螺母
这时螺纹的摩擦阻力为：
Ff f FQ
螺杆 Fn
Fn=FQ
当β≠ 0º时，摩擦力为：
轴 线
β
螺母 FQ
α
这时螺纹的摩擦阻力为：
2、螺纹自锁条件为：
φ≤ρv
三、螺旋副效率为：
Fr
螺旋副的效率问题是由于摩擦引起的： φ
上升：
FQ F
若不考虑摩擦时：F= FQ tan (φ)
Fr φ +ρV
若考虑摩擦时： F= Fa tan (φ +v)
FQ F
在同样的载荷FQ，同样的牵引速度V，走过同 样的距离S情况下：
没有摩擦时，需要的输入功 =FS= FQ S tan (φ) 理论上 考虑摩擦时，需要的输入功
可得： F= FQ tan (ψ -)
ψ
Fn ρ
Fr
v
f Fn

（忽略升角λ的影响）
在Fa的作用下，法向反力比矩形螺纹大为：
Fn
Fa
cos
这时螺纹的摩擦阻力为：
Ff
f Fn Fa
cos
f
f
cos
Fa
f 'Fa
这时把法向力的增加看成摩擦系数的增加。
f ' f tg ' cos
f '称为当量摩擦系数
ρ'称为当量摩擦角
为牙型斜角
用f '取代f，用ρ'取代ρ，就可像矩形螺纹那样对
在同样的载荷Fa，同样的牵引速度V，走过同样 的距离S情况下：
没有摩擦时，需要的输入功 =FS= Fa S tg (ψ) 理论上 考虑摩擦时，需要的输入功
ddd dd2d2 2 dd1d1 1
PPP LL=L=n=nPn(PP(n(n=n=2=)2)2) LLL
ddddd2d22dd1d1 1
hhh
4）螺 距 P — 相邻两牙在中径圆柱面的母线上对应 两点间的轴向距离。 5）导程（S）— 同一螺旋线上相邻两牙在中径圆柱面 的母线上的对应两点间的轴向距离。 6）线数n —螺纹螺旋线数目，一般为便于制造n≤4。
螺距、导程、线数之间关系：S=nP
PPP LL=L=n=nPn(P(Pn(n=n=2=)2)2) LLL
dddd2dd2 2 dd1d1 1
ddddd2d22dd1d1 1
hhh
7）螺旋升角ψ—中径圆柱面上螺旋线的切线与垂直于
螺旋线轴线的平面的夹角。 tgψ =nP/πd2 8）牙型角α—轴向截平面内螺纹牙型相邻两侧边的夹
第二部分 联 接
概述 1 螺纹参数 2 螺旋副的受力分析、效率和自锁 3 机械制造常用螺纹 4 螺纹联接的基本类型及螺纹紧固件 5 螺纹联接的预紧和防松

PPP LL=L=n=nPn(P(Pn(n=n=2=)2)2) LLL
dddd2dd2 2 dd1d1 1
hhh
ddddd2d22dd1d1 1
2 螺旋副的受力分析、 效率和自锁
一、矩形螺纹 二、非矩形螺纹 三、螺旋副效率
一、矩形螺纹（=0)
1、螺纹受力分析
R Fa
Ff F
摩擦角ρ：
Fn
Fr ρ
4、母体形状： 5、按作用： 6、按位置：
圆柱螺纹、圆锥螺纹； 联接螺纹、传动螺纹； 内螺纹、外螺纹；
旋向判断方法：
1、将螺纹轴线竖
直放置，螺旋线自
左向右逐渐升高的
是右旋螺纹。反之
也成立。
左 旋
2、从端部沿轴线
右 旋
看去，当螺纹顺时
针方向旋转为旋进
时，此螺纹为右旋
螺纹。
单线螺纹双线螺纹源自三、螺纹的主要几何参数：dddd2dd2 2 dd1d1 1
ddddd2d22dd1d1 1
hhh
7）螺旋升角ψ—中径圆柱面上螺旋线的切线与垂直于
螺旋线轴线的平面的夹角。 tgψ =nP/πd2 8）牙型角α—轴向截平面内螺纹牙型相邻两侧边的夹
角。牙型侧边与螺纹轴线的垂线间夹角称为牙侧角（牙
型斜角）β。
对称牙侧角β＝ α/2
Fr
v
f Fn F
Fa Fr ψ -ρ
Fa F
2、螺纹自锁：
F= Fa tg (ψ -) 分析：
（1）ψ ->0， ψ> ， F >0
说明滑块在重力作用下下滑，必须给以止动力， 防止加速下滑。
（2）ψ - <0， ψ <， F <0
说明滑块不能在重力作用下下滑。这一现象称 为自锁现象。螺旋千斤顶就是利用这一原理工作的。

套管连接螺纹的受力分析与改善措施作者：杜倩来源：《经济视野》2015年第01期【摘要】油套管柱是由无数的石油专用管材通过螺纹连接在一起组成，套管与螺纹都长期承受着拉伸、压缩、弯曲、内外高温等等情况，由于环境及螺纹结构问题，经常会导致故障，故障原因多为套管连接螺纹的受力问题。

在国外很多时候油套管出现失效事故中故障点百分之六十五以上都是出在螺纹连接处，在我国甚至已经高达百分之八十以上，不得不承认螺纹连接部位是整个油套管柱最薄弱的环境，因此对套管连接螺纹的研究有着重要意义，本文将针对套管连接螺纹的受力与改善措施进行分析和讨论。

【关键词】套管连接受力改善措施引言我国目前在油套管柱中普遍使用的螺纹连接方式有：“特殊螺纹接头连接、圆螺纹接头连接、偏梯形螺纹连头连接”，其中后两种属于API螺纹，第一种特殊螺纹属于专利产品，是由油套管生产厂家研发及生产的。

经过实践及应用的证明API螺纹结构设计存在缺陷，如：连接强度低仅为管体的百分之六十左右，并在密封性上也可靠，另一方面还存在着接头应力水平高、上扣控制难、耐腐性能差等问题。

虽然特殊螺纹针对API进行了强化，达到了API难以比拟的性能，但在使用中依然存在受力等问题，螺纹接头结构是影响套管连接螺纹受力分布的关键。

一、套管连接螺纹的受力分析目前我国在螺纹接头方面的研究起步较晚，技术水平尚未成熟，因此螺纹接头的设计结构、受力优化、密封结构、抗粘扣性方面依然有待加强。

事实上中国是消耗油套管最多的国家之一[1]。

但是我国在特殊螺纹接头研发方面却起步较晚，八十年代我国螺纹接头多靠引进，随着时代的进步，经济的发展，我国的石油工业得到了发展，并且很多时候都是具有高难度的汽油井，因此对螺纹接头的技术要求越来越高，并且数量也越来越大，因此我国对特殊螺纹接头的研究越来越重视，但由于技术问题，所以不管是在质量上还是数量上，都无法满足我国油田的需要，随着我国对螺纹接头研发投资力度的加大，很多开始大力研发特殊螺纹接头。

Q 2

N Q 2 2 N Q 2 2


N Q ＝ 2 2cos
合理使用假设 Q
Q
Q 2
Q 2
F
T
d2 F
合理使用假设
设＝０
Q 2 Q 2 Q 2
Q 2
联接用的螺旋副，紧固物件可自动防松；
螺旋副自锁的用处：
联接用的螺旋副，紧固物件可自动防松； 螺旋千斤顶举重物，可自动防止重物下落。
Q
二、非矩形螺旋副
设＝０
Q 2 Q 2 Q 2
Q 2

Ｎ＝Q
Ff ＝f N ＝ f Q
Q 2 Q 2 Q 2
N＝Q/cos
Ff ＝ f N＝ f Q/cos f Ff Q fvQ cos
R F
F
Q
Q +
1.力关系式
R
N ρ

Ff Q
F
d2 F
2.螺旋副的效率 螺旋副的效率曲线
100 效率h（%）
80
60 40 20 0 10 20
f tan 0.13040 50 60 螺纹升角
70
80
90
3.螺旋副的自锁
N
R

ρ
Ff
F

R
Q
Q
-ρ
F
螺旋副自锁的用处：
第三章 螺纹联接 第一节 螺纹及螺纹参数 第二节 螺旋副的受力分析、效率和自锁
第三章 螺纹联接
第二节 螺旋副的受力分析、效率和自锁
螺旋副
Q
T
螺旋千斤顶
Q
螺旋千斤顶
一、矩形螺旋副 1.力关系式
Q 2
Q 2

螺纹连接受力分析一、螺纹强度校核把螺母得一圈螺纹沿大径展开，螺杆得一圈螺纹沿小径展开，视为悬臂梁，如图。

相关参数：轴向力,旋合螺纹圈数（因为旋合得各圈螺纹牙受力不均,因而不宜大于10）；螺纹牙底宽度,螺纹工作高度,每圈螺纹牙得平均受力为,作用在中径上。

螺母—-内螺纹，大径、中径、小径分别为、、。

螺杆--外螺纹，大径、中径、小径分别为、、。

1.挤压强度螺母一圈挤压面面积为,螺杆一圈挤压面积为。

螺母挤压强度螺杆挤压强度为挤压应力，为许用挤压应力。

2.剪切强度螺母剪切面面积为,螺杆剪切面面积。

螺母，剪切强度螺杆，剪切强度，为材料许用拉应力,为材料屈服应力。

安全系数,一般取３~５.3.弯曲强度危险截面螺纹牙根部，A-A。

螺母,弯曲强度螺杆，弯曲强度其中，：弯曲力臂，螺母，螺杆：弯矩，螺母,螺杆:抗弯模量，螺母,螺杆：螺纹牙得许用弯曲应力，对钢材，4.自锁性能自锁条件，其中，螺旋升角，螺距、导程、线数之间关系：;当量摩擦角,当量摩擦系数为螺旋副得滑动摩擦系数，无量纲,定期润滑条件下,可取0、13~0、17；为牙侧角，为牙型角得一半,5.螺杆强度1、实心螺杆2、空心按实际情况计算3、普通螺纹：普通螺纹螺栓拉断截面,就是一个经验值,其经验计算公式为其中,为材料得许用拉应力，，为屈服应力,为安全系数，一般取3～5。

二、螺栓连接强度6.预紧力计算：一般,螺栓预紧应力可达到材料屈服应力得50％~７０％.：预紧力矩，，为拧紧力系数，为螺纹公称直径，:预紧力，:预紧应力,,为材料屈服应力：螺纹部分危险剖面得面积，:螺纹部分危险剖面得计算直径，,，7.松螺栓连接松螺栓连接,工作载荷，螺栓危险截面强度8.紧螺栓连接紧螺栓连接，无工作载荷时.螺栓危险截面拉伸应力，危险截面扭转切应力根据第四强度理论,螺栓预紧状态下,螺栓危险截面计算应力紧螺栓连接，有轴向工作载荷。

螺栓受力4个量，预紧力，工作载荷，残余预紧力，受载时螺栓总拉力。

螺纹联接的强度计算螺纹联接是一种常用的机械联接方式，广泛应用于各种设备和结构中。

螺纹联接的强度计算是保证螺纹联接安全可靠的重要一环。

下面我将从以下几个方面详细介绍螺纹联接的强度计算。

一、螺纹联接的受力分析：螺纹联接主要受到拉力和剪力的作用，因此在强度计算中，我们需要考虑拉力和剪力产生的影响。

1.拉力：拉力是在螺纹联接中最主要的受力方式。

当联接受到拉力时，螺纹间会产生预紧力，该预紧力可以通过牛顿定律计算。

预紧力会加大螺纹联接的接触应力，并提高联接的强度。

2.剪力：在一些情况下，螺纹联接还会受到剪力的作用，尤其是在动力传递系统和高速旋转机械中。

剪力会导致螺纹断裂，因此在强度计算中需要考虑剪力的影响。

二、螺纹联接的强度计算方法：对于螺纹联接的强度计算，我们可以采用以下两种主要的方法。

1. 经验公式法：基于大量实验数据和实践经验的总结，可以建立起一些经验公式，用于计算螺纹联接的强度。

常用的经验公式有Tresca准则和Von Mises准则。

2.材料力学方法：通过应力和应变的分析，可以采用材料力学的方法来计算螺纹联接的强度。

常见的方法有拉伸强度法、剪切强度法和受约束弹性法等。

不同的计算方法有其适用的条件和限制。

在具体计算时，需要根据实际情况选择适合的计算方法，并考虑螺纹联接的几何尺寸、材料性质、加载方式等因素。

三、螺纹联接的强度计算参数：在进行螺纹联接强度计算时，需要考虑以下几个关键参数。

1.螺纹参数：包括螺纹的规格、高度、宽度、垂直角度等。

这些参数决定了螺纹联接的形状和尺寸，对联接的强度产生重要影响。

2.材料参数：包括螺纹材料的强度、韧性、疲劳寿命等。

这些参数决定了螺纹的承载能力和使用寿命。

3.预紧力：预紧力是指螺纹联接时所加的紧固力。

预紧力的大小直接影响螺纹联接的强度。

预紧力过小会导致松动，过大则会导致断裂。

4.细节参数：包括联接面的光洁度、润滑条件等。

这些细节参数对于螺纹联接的强度也有一定的影响。

四、螺纹联接的强度评估：确定了螺纹联接的强度计算方法和参数后，我们可以进行强度评估。