逻辑推理基本知识

数学中的逻辑推理知识点总结一、引言逻辑推理是数学中重要的思维方式，它涉及到命题、推理规则和推理方法等方面知识。

本文将对数学中的逻辑推理知识点进行总结，帮助读者更好地理解和应用数学中的逻辑推理。

二、命题与逻辑符号命题是陈述性语句，可以判断为真或假。

在数学中，常用字母或字母组合表示命题，在逻辑推理过程中，可以使用逻辑符号对命题进行操作。

常见的逻辑符号包括：1. 否定符号（¬）表示取反；2. 合取符号（∧）表示逻辑与；3. 析取符号（∨）表示逻辑或；4. 条件符号（→）表示蕴含关系；5. 等价符号（↔）表示等价关系。

三、命题联结词及其真值表命题联结词是将多个命题组合成复合命题的符号。

常见的命题联结词有否定（¬）、合取（∧）、析取（∨）、条件（→）、双条件（↔）等。

通过构建命题联结词的真值表，可以确定复合命题的真假。

四、命题的等价关系等价关系是指两个命题在所有情况下都具有相同的真值。

在逻辑推理中，等价关系用双条件符号（↔）表示。

常见的等价关系有以下几种：1. 否定律：¬(p∧q)↔(¬p∨¬q)2. 交换律：(p∧q)↔(q∧p)3. 结合律：((p∧q)∧r)↔(p∧(q∧r))4. 分配律：(p∧(q∨r))↔((p∧q)∨(p∧r))5. 互补律：p∨¬p6. 同一律：p∨T↔T， p∧F↔F五、推理规则推理规则是指根据已知条件和逻辑关系进行推理得出新结论的规则。

在数学中常用的推理规则包括：1. 假言推理：如果p→q是真命题，且已知p为真，则可以推断q为真。

2. 拒取式：如果p→q是真命题，且已知q为假，则可以推断p为假。

3. 析取三段论：如果p∨q为真命题，且已知p为假，q为真，则可以推断q为真。

4. 假言三段论：如果p→q和q→r都是真命题，且已知p为真，则可以推断r为真。

六、数学证明中的逻辑推理逻辑推理在数学证明中起着重要的作用。

数学证明一般包括假设、证明主体和结论等部分，其中证明主体部分的推理过程需要严密的逻辑推理。

判断推理逻辑推理常考知识点一、逻辑推理基本概念。

1. 命题。

- 定义：可以判断真假的陈述句。

例如“今天是晴天”就是一个命题。

- 简单命题：不能再分解为更简单命题的命题。

像“小明是学生”。

- 复合命题：由简单命题通过逻辑联结词组合而成的命题。

如“小明是学生并且小红是老师”，其中“并且”就是逻辑联结词。

2. 逻辑联结词。

- 且（∧）：表示两个命题同时成立。

例如，命题p：小明是男生，命题q：小明是学生，那么p∧q表示小明是男生并且是学生。

当p和q都为真时，p∧q才为真。

- 或（∨）：表示两个命题至少有一个成立。

比如命题p：今天是周一，命题q：今天是周二，p∨q表示今天是周一或者是周二。

只要p、q中有一个为真，p∨q就为真。

- 非（¬）：对一个命题进行否定。

若命题p：小李是好人，那么¬p：小李不是好人。

p为真时，¬p为假；p为假时，¬p为真。

3. 充分条件与必要条件。

- 充分条件：如果有事物情况A，则必然有事物情况B；如果没有事物情况A，但未必没有事物情况B，A就是B的充分而不必要的条件，简称充分条件。

例如，如果天下雨（A），那么地面湿（B），天下雨是地面湿的充分条件。

- 必要条件：如果没有事物情况A，则必然没有事物情况B；如果有事物情况A而未必有事物情况B，A就是B的必要而不充分的条件，简称必要条件。

只有年满18周岁（A），才能有选举权（B），年满18周岁是有选举权的必要条件。

1. 三段论推理。

- 定义：由两个包含着一个共同项的性质判断作前提，得出一个新的性质判断为结论的演绎推理。

例如：所有的金属都能导电（大前提），铜是金属（小前提），所以铜能导电（结论）。

- 规则：- 在一个三段论中，有且只能有三个不同的项。

- 中项在前提中至少要周延一次。

- 在前提中不周延的项，在结论中也不得周延。

- 如果前提中有一个是否定的，那么结论也是否定的；如果结论是否定的，那么前提中必有一个是否定的。

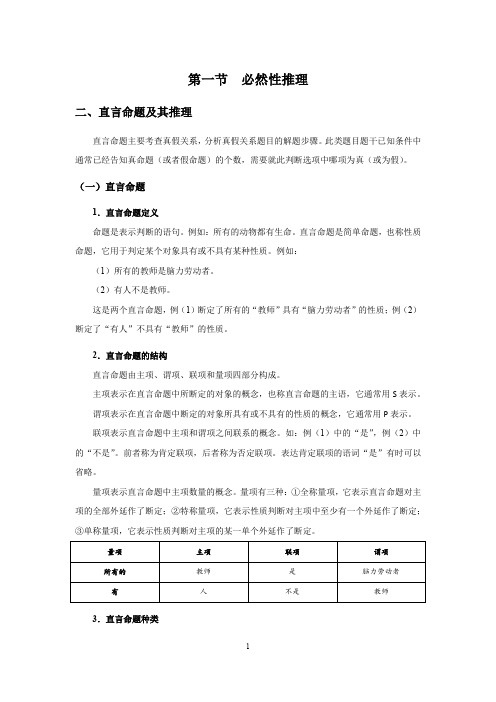
第一节必然性推理二、直言命题及其推理直言命题主要考查真假关系，分析真假关系题目的解题步骤。

此类题目题干已知条件中通常已经告知真命题（或者假命题）的个数，需要就此判断选项中哪项为真（或为假）。

（一）直言命题1．直言命题定义命题是表示判断的语句。

例如：所有的动物都有生命。

直言命题是简单命题，也称性质命题，它用于判定某个对象具有或不具有某种性质。

例如：（1）所有的教师是脑力劳动者。

（2）有人不是教师。

这是两个直言命题，例（1）断定了所有的“教师”具有“脑力劳动者”的性质；例（2）断定了“有人”不具有“教师”的性质。

2．直言命题的结构直言命题由主项、谓项、联项和量项四部分构成。

主项表示在直言命题中所断定的对象的概念，也称直言命题的主语，它通常用S表示。

谓项表示在直言命题中断定的对象所具有或不具有的性质的概念，它通常用P表示。

联项表示直言命题中主项和谓项之间联系的概念。

如：例（1）中的“是”，例（2）中的“不是”。

前者称为肯定联项，后者称为否定联项。

表达肯定联项的语词“是”有时可以省略。

量项表示直言命题中主项数量的概念。

量项有三种：①全称量项，它表示直言命题对主项的全部外延作了断定；②特称量项，它表示性质判断对主项中至少有一个外延作了断定；③单称量项，它表示性质判断对主项的某一单个外延作了断定。

3．直言命题种类根据量项和联项的不同，直言命题可以分为以下六种类型：表2 直言命题种类4．直言命题的真假情况直言命题主项所反映的对象的性质是事物中的一个类，谓项所反映的对象的性质也是事物中的一个类，所以，在直言命题中，主项S与谓项P实质上反映了类与类的关系。

根据上一节所述的概念间的关系可知，类与类之间的关系有全同关系、全异关系、真包含于关系、真包含关系和交叉关系五种，因而直言命题的主项S与谓项P之间在外延上也就只能反映类与类的这五种关系。

根据主、谓项所反映的类与类之间的五种不同关系，以及对它们进一步概括后所得的包含于、非包含于、相容和不相容的四种不同关系，就可以确定A、E、I、O四种性质判断本身的真假。

逻辑基本知识一个符号两种条件A（充分）→B（必要）表必要的词语：基础、关键、前提、必须、需要、离不开、必不可少、不可或缺→，“忠于箭头”肯定向右，否定向左例题无论从全球范围，还是从我国的实际情况来看，人类文明都发展到了这样一个阶段，即保护生态环境，确保人与自然的和谐，是经济能够得到可持续发展的必要前提，也是人类文明得以延续的保证。

由此可以推出：A.如果经济不可持续发展，就是没有搞好环境保护B.只有搞好环境保护，才能实现经济的可持续发展C.即使没有搞好环境保护，也能实现经济的可持续D.只有实现了经济的可持续发展，环境保护才能搞得好是必要前提（=必要条件），谁是必要谁在后。

“经济能够得到可持续发展→保护生态环境”分析选项：A选项，如果...就...，前推后，“-经济能够得到可持续发展->-保护生态环境，不一致”。

错误。

B选项，只有...才...，后推前，“一致”。

正确。

C选项，并列，且关系，“A且-B,与题干矛盾”错误。

D选项，只有...才...，后推前，“保护生态环境->经济可持续发展，不一致”。

错误。

命题形式与真假命题的形式A→B（原命题）等价于-B→-A(逆否命题）-A→-B（否命题）等价于B→A（逆命题）命题的真假A为真 B为真 A->B为真A为真 B为假 A->B为假A为假 B为真 A->B为真A为假 B为假 A->B为真喝酒表三种推理方式演绎推理（三段论）我国的佛教寺庙分布于全国各地，普济寺是我国的佛教寺庙，所以普济寺分布于我国各地。

下列选项中所犯逻辑错误与上述推理最为相似的是：A.父母酗酒的孩子爱冒险，小华爱冒险，所以小华的父母酗酒B.文明公民都是遵纪守法的，有些大学生遵纪守法，所以有些大学生是文明公民C.寒门学子上大学机会减少，大学生小飞不是寒门学子，所以小飞上大学的机会不会减少D.现在的独生子女娇生惯养，何况他还是三代单传的独苗呢D选项，现在的独生子女娇生惯养，何况他还是三代单传的独苗呢=现在的独生子女娇生惯养，他是独生子女，他娇生惯养。

逻辑推理知识点归纳逻辑推理是一种重要的思维方式，它帮助我们更准确地理解和分析问题，从而得出合理的结论。

在日常生活和学业中，逻辑推理都扮演着重要的角色。

本文将对逻辑推理的知识点进行归纳总结，以帮助读者更好地掌握和运用逻辑推理。

一、命题逻辑命题逻辑是逻辑推理中的基础，它研究命题之间的关系和推理规则。

常见的逻辑关系有合取、析取、否定、蕴含等。

1.合取：表示多个命题同时为真，用符号“∧”表示。

例如，“A∧B”表示命题A和命题B同时成立。

2.析取：表示多个命题中至少有一个为真，用符号“∨”表示。

例如，“A∨B”表示命题A和命题B中至少有一个为真。

3.否定：表示一个命题的相反意义，用符号“¬”表示。

例如，“¬A”表示命题A的否定。

4.蕴含：表示一个命题的推理关系，用符号“→”表示。

例如，“A→B”表示如果命题A成立，则命题B也成立。

二、推理方法推理是由一个或多个前提出发，通过逻辑关系得出结论的过程。

推理方法有直接推理、间接推理、假设推理、演绎推理等。

1.直接推理：通过已知的事实或条件直接得出结论。

例如，“如果A>B，而B>C，那么可以得出A>C”。

2.间接推理：通过多个已知事实或条件的中间步骤得出结论。

例如，“已知A>B，B>C，可以通过推理得出A>C”。

3.假设推理：通过对问题进行假设，然后根据假设推理得出结论。

例如，“假设A成立，那么可以得出B成立，再根据B的成立，可以得出C成立”。

4.演绎推理：基于一般规律或普遍原理，从已知的特殊情况推导出结论。

例如，“所有的猫都会喵喵叫，Tom是一只猫，所以Tom会喵喵叫”。

三、逻辑谬误逻辑谬误是在推理过程中出现的错误，它会导致结论的不准确或无效。

常见的逻辑谬误包括偷换概念、诉诸个人攻击、无中生有等。

1.偷换概念：在推理过程中，将问题的核心概念或定义替换为其他相关概念，从而导致结论的不准确。

例如，“要热爱祖国就要支持政府的所有政策”。

小学数学逻辑推理知识大全在小学数学学科中，数学逻辑推理是培养学生思维能力和解决问题能力的重要内容。

通过学习数学逻辑推理知识，学生能够提高自己的思维敏捷性和分析问题的能力。

下面将为大家介绍小学数学逻辑推理知识的大全。

一、数学逻辑推理的基本定义在数学领域，逻辑推理指的是根据已有的条件和已知事实，通过推理和演算，得出新的结论的过程。

数学逻辑推理分为演绎推理和归纳推理两种。

演绎推理基于一般性的前提，通过逻辑上的推导，得出特殊性的结论。

归纳推理则是从一些特殊的个例中归纳出一般的规律。

二、数学逻辑推理的常见题型1. 排列组合题：根据给定的条件，推断出满足条件的可能排列或组合方式。

常见的排列组合题有排队问题、选排问题等。

2. 奇偶性题：通过观察数列中的规律或者进行代入运算，判断数的奇偶性。

例如：在所给数列中，奇数在右边，偶数在左边，请写出可能的数列排列方式。

3. 图形类题目：通过观察图形的特征和规律，找出图形序列中缺失的图形或者下一个图形。

例如：以下图形序列中缺失的图形是什么？4. 推理类题目：通过一系列已知条件，推断出未知条件或者结论。

例如：甲、乙、丙、丁四人比赛，已知丁赢了乙，乙赢了丙，那么谁是冠军？5. 逻辑类题目：通过推理和逻辑关系，得出结论。

例如：如果“A>B”，“B>C”，那么“A>C”是否成立？三、数学逻辑推理的解题方法1. 观察法：通过观察题干中的数学模式、规律和特征，得出结论。

2. 推理法：根据已知条件，运用逻辑关系进行推导和推理，得出结论。

3. 分类法：将题干中的元素进行分类，通过分类分析，找出规律和共性特征。

4. 反证法：假设结论不成立，通过逻辑推理得出矛盾，因此原命题成立。

五、数学逻辑推理的训练方法1. 反复练习典型题目，掌握解题技巧和方法。

2. 注意总结规律和特点，形成思维习惯。

3. 经常进行思维训练和逻辑推理的练习，提高解题能力。

4. 参加数学逻辑推理的比赛和活动，提高竞技水平。

逻辑推理与问题解决知识点总结逻辑推理与问题解决是我们在日常生活和学习中经常遇到的一种思维方式。

通过逻辑推理，可以帮助我们分析问题、找出解决方法，并作出合理的判断。

在本文中，我将对逻辑推理与问题解决的相关知识点进行总结，以帮助读者更好地掌握这一技巧。

一、逻辑推理的基本规则逻辑推理是基于一定的规则和原则进行的，其中最基本的规则包括：1. 充分必要条件：若A是B的充分条件，则B是A的必要条件。

如：学习努力是取得好成绩的充分条件，那么取得好成绩是学习努力的必要条件。

2. 假言命题：若前件为真，则结论为真。

如：如果明天下雨，那么我会带雨伞。

3. 假言推理：由若干假设推导出一个结论。

如：如果今天下雨，那么我就不出门，今天下雨，所以我不出门。

4. 反证法：通过反设假设的方式，推导出矛盾，从而证明原命题。

如：假设A成立，若能推出B不成立，则可以通过反证法证明A不成立。

通过掌握这些基本规则，我们可以更加准确地进行逻辑推理，解决各种问题。

二、问题解决的思维方法问题解决通常需要经过一系列的思考和分析过程，以下是几种常用的思维方法：1. 辨析问题：首先要明确问题的核心，搞清楚问题的本质，避免问题的偏离。

2. 分解问题：将一个大问题分解为多个小问题，逐个解决，这样可以降低解决问题的难度。

3. 归纳和演绎：通过观察和实践，总结出一般规律，并利用这些规律进行推演，解决实际问题。

4. 借鉴经验：通过学习和借鉴他人的经验，可以更好地解决问题。

尤其是遇到已被解决过的类似问题时，可以借鉴前人的经验和成果，节省时间和精力。

5. 创新思维：在问题解决过程中，不断尝试新的思路和方法，开拓思维的边界，从而找到更好的解决方案。

三、逻辑推理与问题解决的应用领域逻辑推理与问题解决的应用领域非常广泛，以下是一些常见的应用领域：1. 数学问题：在解决数学问题时，逻辑推理和问题解决思维是必不可少的。

通过运用逻辑推理方法，可以帮助我们理解数学问题并找到解决方法。

推理必背知识点总结一、命题推理1. 命题和命题演算命题是陈述语言的有真假性的陈述。

命题演算是对命题进行逻辑演算的方法。

常见的命题演算方法有合取、析取、条件命题和双条件命题。

2. 命题的连接词命题的连接词是逻辑运算符号，包括合取命题的∧、析取命题的∨、条件命题的→和双条件命题的↔。

3. 命题的混合连接当多个命题混合连接在一起时，需要注意连接词的优先级和括号的使用。

例如：(p∧q)∨r，先计算括号内的命题，再计算整个命题的值。

4. 命题的真值表真值表是对于给定的若干命题，列出所有可能情况下的真值的表格。

通过真值表可以判断复合命题在各种情况下的真假性。

5. 命题的推理基于命题演算的推理方法包括：简单推理、析取范式、合取范式、命题条件和德摩根定律等。

通过这些方法，可以得出结论，解决问题。

二、谬误推理1. 谬误的概念谬误是指在推理过程中出现的错误。

谬误分为形式谬误和实质谬误。

2. 形式谬误形式谬误是推理的结构不当或不完整，从而导致结论无法成立的错误。

如：偷换概念、假设不当、悖论等。

3. 实质谬误实质谬误是推断的前提不实或逻辑错误，导致结论不成立的错误。

如：抽象谬误、依据谬误、偷换概念等。

4. 谬误的检验和纠正检验谬误要对推理过程进行批判性思考，检查前提是否成立，结论是否合理。

纠正谬误需要重新分析问题，发现并修正推理过程中的逻辑错误。

三、数理逻辑1. 命题逻辑和谓词逻辑命题逻辑是处理命题间关系的逻辑。

谓词逻辑是对命题中的元素进行描述和关系的逻辑。

2. 命题逻辑的基本命题形式基本命题形式包括命题的合取、析取、条件命题和双条件命题。

3. 范式和析取范式范式是用合取命题和析取命题来表示一个复合的命题。

析取范式是用析取式来表示一个命题。

4. 命题逻辑的推理通过范式和析取范式，可以进行复杂命题的推理和逻辑演算。

5. 谓词逻辑的概念谓词逻辑是一种用来描述元素和关系的逻辑，主要包括：函项、量词、命题变元、量化和谓词符号等。

小学数学逻辑推理知识点整理数学是一门理性思维的学科，其中的逻辑推理是数学思维的重要组成部分。

逻辑推理能够培养学生的思维能力、观察力和分析能力，帮助他们理解和解决问题。

在小学数学教学中，逻辑推理也是不可或缺的一环。

下面，我将整理一些小学数学中常见的逻辑推理知识点。

1. 数字规律数字规律是小学数学中重要的逻辑推理知识点之一。

通过观察数字的变化规律，学生可以推理出下一个数字。

例如，给出一个数字序列：2，4，6，8，__，学生可以通过观察到每个数字都比前一个数字大2，因此下一个数字应该是10。

这种数字规律的训练可以帮助学生提高观察力和分析能力。

2. 图形推理图形推理是小学数学中常见的逻辑思维题型。

通过观察图形的形状、结构、大小等特点，学生可以推理出下一个图形。

例如，给出一系列图形：正方形，正方形，长方形，正方形，__，学生可以推理出下一个图形应该是正方形，因为这个序列在形状上有规律：正方形，正方形，长方形，正方形，正方形。

图形推理可以帮助学生培养空间思维和观察力。

3. 题意理解在小学数学中，题意理解是解题的重要环节。

学生需要通过阅读和理解题目描述，把握问题的核心内容。

理解题目的特点和要求可以帮助学生进行正确的逻辑推理。

例如，给出一个问题：小明家有8个苹果，他吃掉了3个，那么还剩下__个。

学生需要理解题目中给出的初始条件和要求，通过减法进行逻辑推理，得出答案为5。

题意理解是培养学生逻辑思维和解决问题能力的重要一环。

4. 条件判断条件判断是数学逻辑推理中非常常见的一种形式。

学生需要根据已知的条件推断出结果。

例如，给出一个问题：如果1只鸭子的体重是2千克，那么20只鸭子的体重是多少千克？学生需要根据已知条件（1只鸭子的体重是2千克）和问题的要求进行逻辑推理，得出结果是40千克。

条件判断可以培养学生的逻辑思维和分析能力。

5. 推理证明在小学数学中，推理证明是数学逻辑推理的高阶能力要求。

学生需要通过已知条件和推理过程，来得出结论。

行测逻辑推理知识点
1. 概念关系这可是很重要的呢！比如说，苹果和水果，苹果就是水果这个概念里的具体例子呀。

这不就像班级里的你是学生的一员一样嘛。

2. 充分条件和必要条件，哎呀呀，就像你要去一个好玩的地方，有地图就是充分条件，而你要出门那就是必要条件。

想想看，没地图也可能找到，但不出门怎么去呀！
3. 翻译推理，可以这样理解啦，把一些话变成特定的公式来推理，就好像把复杂的密码解开一样。

比如说“如果下雨就带伞”，一旦下雨，不就得带伞嘛。

4. 真假推理超有趣的哦！就跟分辨真假话游戏似的。

比如有几个人说话，有的真有的假，你得找出真相呀。

5. 归纳推理啊，就好像总结一堆事情的共同点或规律。

好比你观察一群动物，总结出它们的一些习性特点呢。

6. 削弱论证就像是给一个说法挑刺儿。

比如说有人说这个东西特别好，你找出一些例子证明它没那么好，不就削弱了嘛。

7. 加强论证呢，相反啦，是给一个说法找支持的证据。

像有人说这个计划很棒，你找到很多证据说明它确实很棒，就是加强啦。

我的观点结论就是：这些行测逻辑推理知识点真的很有意思，好好掌握它们，对解决各种问题都很有帮助哒！。