小学奥数几何图形大全
- 格式:doc
- 大小:147.00 KB
- 文档页数:6
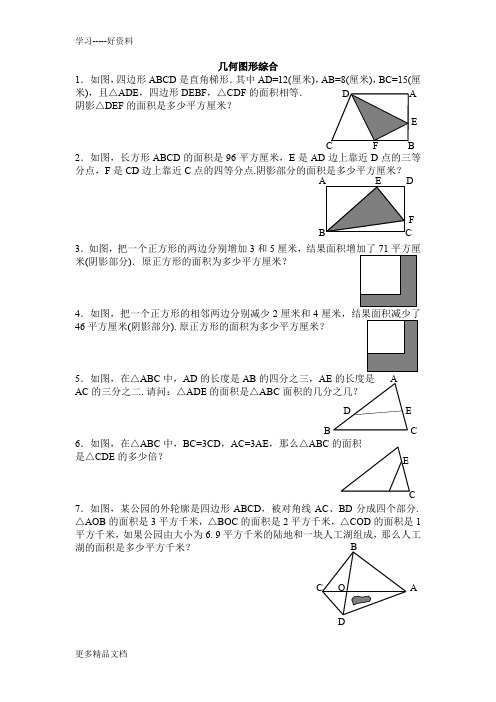
学习-----好资料几何图形综合1.如图,四边形ABCD 是直角梯形.其中AD=12(厘米),AB=8(厘米),BC=15(厘米),且△ADE ,四边形DEBF ,△CDF 的面积相等. 阴影△DEF 的面积是多少平方厘米?2.如图,长方形ABCD 的面积是96平方厘米,E 是AD 边上靠近D 点的三等分点,F 是CD 边上靠近C 点的四等分点.阴影部分的面积是多少平方厘米?3.如图,把一个正方形的两边分别增加3和5厘米,米(阴影部分).原正方形的面积为多少平方厘米?4.如图,把一个正方形的相邻两边分别减少2厘米和446平方厘米(阴影部分).原正方形的面积为多少平方厘米?5.如图,在△ABC 中,AD 的长度是AB 的四分之三,AE 的长度是 AC 的三分之二.请问:△ADE 的面积是△ABC 面积的几分之几?6.如图,在△ABC 中,BC=3CD ,AC=3AE ,那么△ABC 的面积是△CDE 的多少倍?7.如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分.△AOB 的面积是3平方千米,△BOC 的面积是2平方千米,△COD 的面积是1平方千米,如果公园由大小为6.9平方千米的陆地和一块人工湖组成,那么人工湖的面积是多少平方千米?E DF B CA D E AB CE A D学习-----好资料8.如图,在梯形ABCD 中,AD 长9厘米,BC 长15厘米, BD 长12厘米,那么OD 长多少厘米? 9.如图,有8个半径为1厘米的小圆,用它们圆周的一部分 连成一个花瓣图形,图中的黑点是这些圆的圆心.如果圆周率 π取3.14,那么花瓣图形的周长和面积分别是多少? 10.图中甲区域比乙区域的面积大57其中直角三角形竖直的直角边的长度是多少?(π取3.14) 11.如图,在3×3的方格表中,分别以A 、E 为圆心,3、2为半径,画出圆心角都是90º的两段圆弧.图中阴影部分的面积是多少? (π取3.14).(π取13.下图是一个直角边长为3厘米、4厘米的直角三角形.将该三角形一任意一条边所在直线为轴进行旋转,求所得立体图形的表面积和体积.14.如图,已知正方形ABCD 的边长为4厘米,求阴影部分的面积.A D OB C● ● ●● ● ●● ● ● ● ● ● ● ● ●a bc d e f hg15.斜边长为10厘米的等腰直角三角形的面积是多少?16.右图中两个完全相同的三角形重叠在一起,则阴影部分的面积是多少?17.求图中四边形的面积.18.图中八条边的长度正好分别是1,2,3,4,5,6,7,8厘米. 已知a =2厘米,b=4厘米,c =5厘米,求图形的面积.19.如图所示,∠1+∠2+∠3+∠4+∠5+∠6等于多少度?20.如图,一个边长为1米的正方形被分成4个小长方形,它们的面积分别是0.3平方米、0.4平方米、0.2平方米、0.1平方米. 已知图中的阴影部分是正方形,那么它的面积是多少平方米?21.如图所示,三角形ABC 中,DE 与BC 平行,且AD :DB=5求AE :EC 及DE :BC .22.如图,间相互重叠.已知露在外面的部分中,红色的面积是20,黄色的面积是14,绿色的面积是10.那么,B A D 1 2 3 4 5 6 绿23.如图所示,已知△ABC 的面积为1平方厘米,D 、E是AB 、AC 边的中点.求三角形OBC 的面积.24.在如图所示的正方形中,A 、B 、C 分别是ED 、EG 、GF的中点.请问:△CDO 的面积是△ABO 面积的几倍?25.如图,四边形ABCD 是平行四边形,面积为72平方厘米,E 、F 分别为边AB 、BC 的中点,请问:阴影部分的面积为多少平方厘米?26.如图,△ABC 中,CE=2AE ,F 是AD的中点,△ABC 为1,那么阴影部分的面积多少?27.如图,△ABC 中,AD 、BE 相交于点O ,△OAE 、△OAB△OBD 的面积分别为1、2、3,那么四边形ODCE28.图中有半径分别为5厘米、4厘米、3厘米的三个圆,A 部分(即两小圆重叠部分)的面积与阴影部分的面积相比,哪个大?大多少?29.如图,图中最大的长方形面积是27,最小的长方形面积是5面积.30.阅读理解:(1)阅读:勾股定理是几何学中一颗光彩夺目的明珠,被称为“几何学的基石”,中国是发现和研究勾股定理最古老的国家之一。

⼩学奥数⼏何图形⼤全⼏何图形综合1.如图,四边形ABCD 是直⾓梯形.其中AD=12(厘⽶),AB=8(厘⽶),BC=15(厘⽶),且△ADE ,四边形DEBF ,△CDF 的⾯积相等.阴影△DEF 的⾯积是多少平⽅厘⽶?2.如图,长⽅形ABCD 的⾯积是96平⽅厘⽶,E 是AD 边上靠近D 点的三等分点,F 是CD 边上靠近C 点的四等分点.阴影部分的⾯积是多少平⽅厘⽶?3.如图,把⼀个正⽅形的两边分别增加3和5厘⽶,⽶(阴影部分).原正⽅形的⾯积为多少平⽅厘⽶?4.如图,把⼀个正⽅形的相邻两边分别减少2厘⽶和446平⽅厘⽶(阴影部分).原正⽅形的⾯积为多少平⽅厘⽶?5.如图,在△ABC 中,AD 的长度是AB 的四分之三,AE 的长度是 AC 的三分之⼆.请问:△ADE 的⾯积是△ABC ⾯积的⼏分之⼏?6.如图,在△ABC 中,BC=3CD ,AC=3AE ,那么△ABC 的⾯积是△CDE 的多少倍?7.如图,某公园的外轮廓是四边形ABCD ,被对⾓线AC 、BD 分成四个部分.△AOB 的⾯积是3平⽅千⽶,△BOC 的⾯积是2平⽅千⽶,△COD 的⾯积是1平⽅千⽶,如果公园由⼤⼩为6.9平⽅千⽶的陆地和⼀块⼈⼯湖组成,那么⼈⼯湖的⾯积是多少平⽅千⽶?E DF B CA D E AB CE A D8.如图,在梯形ABCD 中,AD 长9厘⽶,BC 长15厘⽶, BD 长12厘⽶,那么OD 长多少厘⽶? 9.如图,有8个半径为1厘⽶的⼩圆,⽤它们圆周的⼀部分连成⼀个花瓣图形,图中的⿊点是这些圆的圆⼼.如果圆周率π取3.14,那么花瓣图形的周长和⾯积分别是多少? 10.图中甲区域⽐⼄区域的⾯积⼤57其中直⾓三⾓形竖直的直⾓边的长度是多少?(π取3.14) 11.如图,在3×3的⽅格表中,分别以A 、E 为圆⼼,3、2为半径,画出圆⼼⾓都是90o的两段圆弧.图中阴影部分的⾯积是多少? (π取3.14).(π取13.下图是⼀个直⾓边长为3厘⽶、4厘⽶的直⾓三⾓形.将该三⾓形⼀任意⼀条边所在直线为轴进⾏旋转,求所得⽴体图形的表⾯积和体积.14.如图,已知正⽅形ABCD 的边长为4厘⽶,求阴影部分的⾯积.A D OB C●●●●●●●●●●●●●●●a bc d e f hg15.斜边长为10厘⽶的等腰直⾓三⾓形的⾯积是多少?16.右图中两个完全相同的三⾓形重叠在⼀起,则阴影部分的⾯积是多少?17.求图中四边形的⾯积.18.图中⼋条边的长度正好分别是1,2,3,4,5,6,7,8厘⽶. 已知a =2厘⽶,b=4厘⽶,c =5厘⽶,求图形的⾯积.19.如图所⽰,∠1+∠2+∠3+∠4+∠5+∠6等于多少度?20.如图,⼀个边长为1⽶的正⽅形被分成4个⼩长⽅形,它们的⾯积分别是0.3平⽅⽶、0.4平⽅⽶、0.2平⽅⽶、0.1平⽅⽶. 已知图中的阴影部分是正⽅形,那么它的⾯积是多少平⽅⽶?21.如图所⽰,三⾓形ABC 中,DE 与BC 平⾏,且AD :DB=5求AE :EC 及DE :BC .22.如图,间相互重叠.已知露在外⾯的部分中,红⾊的⾯积是20,黄⾊的⾯积是14,绿⾊的⾯积是10.那么,B A D 1 2 3 4 5 6 绿23.如图所⽰,已知△ABC 的⾯积为1平⽅厘⽶,D 、E是AB 、AC 边的中点.求三⾓形OBC 的⾯积.24.在如图所⽰的正⽅形中,A 、B 、C 分别是ED 、EG 、GF的中点.请问:△CDO 的⾯积是△ABO ⾯积的⼏倍?25.如图,四边形ABCD 是平⾏四边形,⾯积为72平⽅厘⽶,E 、F 分别为边AB 、BC 的中点,请问:阴影部分的⾯积为多少平⽅厘⽶?26.如图,△ABC 中,CE=2AE ,F 是AD的中点,△ABC 为1,那么阴影部分的⾯积多少?27.如图,△ABC 中,AD 、BE 相交于点O ,△OAE 、△OAB△OBD 的⾯积分别为1、2、3,那么四边形ODCE28.图中有半径分别为5厘⽶、4厘⽶、3厘⽶的三个圆,A 部分(即两⼩圆重叠部分)的⾯积与阴影部分的⾯积相⽐,哪个⼤?⼤多少?29.如图,图中最⼤的长⽅形⾯积是27,最⼩的长⽅形⾯积是5⾯积.30.阅读理解:(1)阅读:勾股定理是⼏何学中⼀颗光彩夺⽬的明珠,被称为“⼏何学的基⽯”,中国是发现和研究勾股定理最古⽼的国家之⼀。

目录目录 (1)模型一——《等积变换》 (2)一、知识点梳理 (2)二、例题精讲 (3)三、自我提升 (5)四、答案与解析 (7)模型二——《一半模型》 (11)一、知识点梳理 (11)二、例题精讲 (13)三、自我提升 (15)四、答案与解析 (16)模型三——《鸟头(共角)模型》 (19)一、知识点梳理 (19)二、例题精讲 (20)三、自我提升 (22)四、答案与解析 (24)模型四——《蝴蝶模型》 (25)一、知识点梳理 (25)二、例题精讲 (26)模型五——《沙漏模型》 (32)一、知识点梳理 (32)二、例题精讲 (32)三、自我提升 (35)四、答案与解析 (36)模型六——《燕尾模型》 (38)一、知识点梳理 (38)二、例题精讲 (39)三、自我提升 (41)四、答案与解析 (43)模块七——《长、正方体、圆柱、圆锥》 (45)一、知识点梳理 (45)二、例题精讲 (46)三、自我提升 (48)四、自我提升答案 (50)模型八——《圆、扇形》 (52)一、知识点梳理 (52)二、例题精讲 (53)三、自我提升 (55)四、答案与解析 (57)模型一——《等积变换》一、知识点梳理二、例题精讲三、自我提升四、答案与解析模型二——《一半模型》一、知识点梳理一半模型其实是等积变换模型的延伸,只是将三角形和平行四边形进行了整合与综合考查,但是学生往往遇到此类题目之后很难想到用等积变换,所以我们专门提炼出一半模型,帮助学生加深此部分知识点的理解,提高应用能力。
21b a ba ⨯⨯====⨯=∆∆∆∆BCP S BCD S BCF S BCE S ABCD S 口 平行四边形同理不规则图形ba 21b2b1a 21b2a 21b1a 21b2a 21b1a 21ba ⨯=+⨯=⨯⨯+⨯=+=⨯⨯=⨯=⨯=∆∆∆∆)(阴影;口BCE S ADE S BCE S ADE S ABCD S 拓展图形(比例应用)ba 41b2b1a 41b2221b1221b2221b1221b41b 221⨯=+⨯=⨯⨯+⨯⨯=+=⨯⨯=⨯⨯=⨯=⨯⨯==∆∆∆∆∆)(阴影;右图:左图:阴影a a BEG S AFG S aBEG S a AFG S a a BFE S常见图形的认识二、例题精讲例1如图所示,四边形ABCD与AEGF都是平行四边形,请你证明它们的面积相等.例2如图所示,正方形ABCD的边长为8厘米,长方形EBGF的长BG为10厘米,那么长方形的宽为几厘米?例3如图,正方形ABCD的边长为6,AE=1.5,CF=2.长方形EFGH的面积为.例4图中两个正方形的边长分别是6厘米和4厘米,则图中阴影部分三角形的面积是多少平方厘米.A BG CEFDHGFEDCBAGFED CBA例5正方形ABCD 和正方形CEFG ,且正方形ABCD 边长为10厘米,则图中阴影面积为多少平方厘米?例6如图,长方形ABCD 的面积是56平方厘米,点E 、F 、G 分别是长方形ABCD 边上的中点,H 为AD 边上的任意一点,求阴影部分的面积例7 如图,有三个正方形的顶点D 、G 、K 恰好在同一条直线上,其中正方形GFEB 的边长为10厘米,求阴影部分的面积.E BA KEBA三、自我提升1、右图是由大、小两个正方形组成的,小正方形的边长是4厘米,求三角形ABC 的面积.2、如图,ABCD 与AEFG 均为正方形,三角形ABH 的面积为6平方厘米,图中阴影部分的面积为 .3、长方形ABCD 的面积是2011平方厘米.梯形AFGE 的顶点F 在BC 上,D 是腰EG 的中点.试求梯形AFGE 的面积.G4AB CDEF A B C D E FG H4、已知正方形ABCD 边长为10,正方形BEFG 边长为6,求阴影部分的面积.5、右图中,ABCD 和CGEF 是两个正方形,AG 和CF 相交于H ,已知CH 等于CF 的三分之一,三角形CHG 的面积等于6平方厘米,求五边形ABGEF 的面积.6、如图,正方形ABCG 和正方形FCDE 并排放置,BE 与FC 相交于点H ,已知AB=6厘米,则阴影部分的面积是_________________平方厘米? 四、答案与解析1、【分析】如图所示,连接AD ,则BC 平行AD ,三角形ABC 和三角形BCD 等底等高,因此三角形ABCJIHGA BCD EF HG F E D C B A的面积就等于小正方形的面积的一半,据此即可得解.解:据分析可知:4×4÷2=8(平方厘米);答:三角形ABC的面积是8平方厘米.2、【分析】方法一:如图所示,连接AF和BD,则AF平行BD,三角形FAD与三角形FAB等底等高,即面积相同。

目录目录 (1)模型一——《等积变换》 (2)一、知识点梳理 (2)二、例题精讲 (3)三、自我提升 (5)四、答案与解析 (7)模型二——《一半模型》 (11)一、知识点梳理 (11)二、例题精讲 (13)三、自我提升 (15)四、答案与解析 (16)模型三——《鸟头(共角)模型》 (19)一、知识点梳理 (19)二、例题精讲 (20)三、自我提升 (22)四、答案与解析 (24)模型四——《蝴蝶模型》 (25)一、知识点梳理 (25)二、例题精讲 (26)模型五——《沙漏模型》 (32)一、知识点梳理 (32)二、例题精讲 (32)三、自我提升 (35)四、答案与解析 (36)模型六——《燕尾模型》 (38)一、知识点梳理 (38)二、例题精讲 (39)三、自我提升 (41)四、答案与解析 (43)模块七——《长、正方体、圆柱、圆锥》 (45)一、知识点梳理 (45)二、例题精讲 (46)三、自我提升 (48)四、自我提升答案 (50)模型八——《圆、扇形》 (52)一、知识点梳理 (52)二、例题精讲 (53)三、自我提升 (55)四、答案与解析 (57)模型一——《等积变换》一、知识点梳理二、例题精讲三、自我提升四、答案与解析模型二——《一半模型》一、知识点梳理一半模型其实是等积变换模型的延伸,只是将三角形和平行四边形进行了整合与综合考查,但是学生往往遇到此类题目之后很难想到用等积变换,所以我们专门提炼出一半模型,帮助学生加深此部分知识点的理解,提高应用能力。
21b a ba ⨯⨯====⨯=∆∆∆∆BCP S BCD S BCF S BCE S ABCD S 口 平行四边形同理不规则图形ba 21b2b1a 21b2a 21b1a 21b2a 21b1a 21ba ⨯=+⨯=⨯⨯+⨯=+=⨯⨯=⨯=⨯=∆∆∆∆)(阴影;口BCE S ADE S BCE S ADE S ABCD S 拓展图形(比例应用)ba 41b2b1a 41b2221b1221b2221b1221b41b 221⨯=+⨯=⨯⨯+⨯⨯=+=⨯⨯=⨯⨯=⨯=⨯⨯==∆∆∆∆∆)(阴影;右图:左图:阴影a a BEG S AFG S aBEG S a AFG S a a BFE S常见图形的认识二、例题精讲例1如图所示,四边形ABCD与AEGF都是平行四边形,请你证明它们的面积相等.例2如图所示,正方形ABCD的边长为8厘米,长方形EBGF的长BG为10厘米,那么长方形的宽为几厘米?例3如图,正方形ABCD的边长为6,AE=1.5,CF=2.长方形EFGH的面积为.例4图中两个正方形的边长分别是6厘米和4厘米,则图中阴影部分三角形的面积是多少平方厘米.A BG CEFDHGFEDCBAGFED CBA例5正方形ABCD 和正方形CEFG ,且正方形ABCD 边长为10厘米,则图中阴影面积为多少平方厘米?例6如图,长方形ABCD 的面积是56平方厘米,点E 、F 、G 分别是长方形ABCD 边上的中点,H 为AD 边上的任意一点,求阴影部分的面积例7 如图,有三个正方形的顶点D 、G 、K 恰好在同一条直线上,其中正方形GFEB 的边长为10厘米,求阴影部分的面积.E BA KEBA三、自我提升1、右图是由大、小两个正方形组成的,小正方形的边长是4厘米,求三角形ABC 的面积.2、如图,ABCD 与AEFG 均为正方形,三角形ABH 的面积为6平方厘米,图中阴影部分的面积为 .3、长方形ABCD 的面积是2011平方厘米.梯形AFGE 的顶点F 在BC 上,D 是腰EG 的中点.试求梯形AFGE 的面积.G4AB CDEF A B C D E FG H4、已知正方形ABCD 边长为10,正方形BEFG 边长为6,求阴影部分的面积.5、右图中,ABCD 和CGEF 是两个正方形,AG 和CF 相交于H ,已知CH 等于CF 的三分之一,三角形CHG 的面积等于6平方厘米,求五边形ABGEF 的面积.6、如图,正方形ABCG 和正方形FCDE 并排放置,BE 与FC 相交于点H ,已知AB=6厘米,则阴影部分的面积是_________________平方厘米? 四、答案与解析1、【分析】如图所示,连接AD ,则BC 平行AD ,三角形ABC 和三角形BCD 等底等高,因此三角形ABCJIHGA BCD EF HG F E D C B A的面积就等于小正方形的面积的一半,据此即可得解.解:据分析可知:4×4÷2=8(平方厘米);答:三角形ABC的面积是8平方厘米.2、【分析】方法一:如图所示,连接AF和BD,则AF平行BD,三角形FAD与三角形FAB等底等高,即面积相同。

小学奥数几何题100道及答案(完整版)题目1:一个正方形的边长是5 厘米,它的面积是多少平方厘米?解题方法:正方形面积= 边长×边长,即5×5 = 25(平方厘米)答案:25 平方厘米题目2:一个长方形的长是8 分米,宽是6 分米,它的周长是多少分米?解题方法:长方形周长= (长+ 宽)×2,即(8 + 6)×2 = 28(分米)答案:28 分米题目3:一个三角形的底是10 厘米,高是6 厘米,它的面积是多少平方厘米?解题方法:三角形面积= 底×高÷2,即10×6÷2 = 30(平方厘米)答案:30 平方厘米题目4:一个平行四边形的底是12 米,高是8 米,它的面积是多少平方米?解题方法:平行四边形面积= 底×高,即12×8 = 96(平方米)答案:96 平方米题目5:一个梯形的上底是 4 厘米,下底是6 厘米,高是5 厘米,它的面积是多少平方厘米?解题方法:梯形面积= (上底+ 下底)×高÷2,即(4 + 6)×5÷2 = 25(平方厘米)答案:25 平方厘米题目6:一个圆的半径是3 厘米,它的面积是多少平方厘米?解题方法:圆的面积= π×半径²,即3.14×3²= 28.26(平方厘米)答案:28.26 平方厘米题目7:一个半圆的半径是 4 分米,它的周长是多少分米?解题方法:半圆的周长= 圆周长的一半+ 直径,即3.14×4×2÷2 + 4×2 = 20.56(分米)答案:20.56 分米题目8:一个长方体的长、宽、高分别是5 厘米、4 厘米、3 厘米,它的表面积是多少平方厘米?解题方法:长方体表面积= (长×宽+ 长×高+ 宽×高)×2,即(5×4 + 5×3 + 4×3)×2 = 94(平方厘米)答案:94 平方厘米题目9:一个正方体的棱长是6 分米,它的体积是多少立方分米?解题方法:正方体体积= 棱长³,即6³= 216(立方分米)答案:216 立方分米题目10:一个圆柱的底面半径是2 厘米,高是5 厘米,它的侧面积是多少平方厘米?解题方法:圆柱侧面积= 底面周长×高,底面周长= 2×3.14×2,即2×3.14×2×5 = 62.8(平方厘米)答案:62.8 平方厘米题目11:一个圆锥的底面半径是3 厘米,高是4 厘米,它的体积是多少立方厘米?解题方法:圆锥体积= 1/3×底面积×高,底面积= 3.14×3²,即1/3×3.14×3²×4 = 37.68(立方厘米)答案:37.68 立方厘米题目12:两个边长为4 厘米的正方形拼成一个长方形,长方形的长和宽分别是多少?面积是多少?解题方法:长方形的长为8 厘米,宽为4 厘米,面积= 8×4 = 32(平方厘米)答案:长8 厘米,宽4 厘米,面积32 平方厘米题目13:一个三角形的面积是18 平方厘米,底是6 厘米,高是多少厘米?解题方法:高= 面积×2÷底,即18×2÷6 = 6(厘米)答案:6 厘米题目14:一个平行四边形的面积是24 平方米,底是 4 米,高是多少米?解题方法:高= 面积÷底,即24÷4 = 6(米)答案:6 米题目15:一个梯形的面积是30 平方分米,上底是5 分米,下底是7 分米,高是多少分米?解题方法:高= 面积×2÷(上底+ 下底),即30×2÷(5 + 7)= 5(分米)答案:5 分米题目16:一个圆环,外圆半径是5 厘米,内圆半径是 3 厘米,圆环的面积是多少平方厘米?解题方法:圆环面积= 外圆面积-内圆面积,即 3.14×(5²- 3²)= 50.24(平方厘米)答案:50.24 平方厘米题目17:一个长方体的棱长总和是48 厘米,长、宽、高的比是3:2:1,长方体的体积是多少立方厘米?解题方法:一条长、宽、高的和为48÷4 = 12 厘米,长为6 厘米,宽为4 厘米,高为2 厘米,体积= 6×4×2 = 48(立方厘米)答案:48 立方厘米题目18:一个正方体的表面积是54 平方分米,它的一个面的面积是多少平方分米?解题方法:一个面的面积= 表面积÷6,即54÷6 = 9(平方分米)答案:9 平方分米题目19:一个圆柱的底面直径是4 分米,高是3 分米,它的表面积是多少平方分米?解题方法:底面积= 3.14×(4÷2)²= 12.56 平方分米,侧面积= 3.14×4×3 = 37.68 平方分米,表面积= 2×12.56 + 37.68 = 62.8(平方分米)答案:62.8 平方分米题目20:一个圆锥的底面周长是18.84 分米,高是5 分米,它的体积是多少立方分米?解题方法:底面半径= 18.84÷3.14÷2 = 3 分米,体积= 1/3×3.14×3²×5 = 47.1(立方分米)答案:47.1 立方分米题目21:一个长方体的水箱,长 5 分米,宽4 分米,高 3 分米,里面装满水,把水倒入一个棱长为5 分米的正方体水箱,水深多少分米?解题方法:水的体积= 5×4×3 = 60 立方分米,正方体水箱底面积= 5×5 = 25 平方分米,水深= 60÷25 = 2.4 分米答案:2.4 分米题目22:一块长方形的铁皮,长8 分米,宽6 分米,从四个角各切掉一个边长为1 分米的正方形,然后做成一个无盖的盒子,这个盒子的容积是多少立方分米?解题方法:盒子长6 分米,宽4 分米,高1 分米,容积= 6×4×1 = 24(立方分米)答案:24 立方分米题目23:一个圆柱的体积是60 立方厘米,底面积是12 平方厘米,高是多少厘米?解题方法:高= 体积÷底面积,即60÷12 = 5(厘米)答案:5 厘米题目24:一个圆锥和一个圆柱等底等高,圆柱的体积是27 立方分米,圆锥的体积是多少立方分米?解题方法:等底等高的圆锥体积是圆柱体积的1/3,即27×1/3 = 9(立方分米)答案:9 立方分米题目25:把一个棱长为 6 厘米的正方体铁块熔铸成一个底面积为36 平方厘米的圆柱体,这个圆柱体的高是多少厘米?解题方法:正方体体积= 6³= 216 立方厘米,圆柱体的高= 体积÷底面积,即216÷36 = 6(厘米)答案:6 厘米题目26:一个直角三角形的两条直角边分别是3 厘米和4 厘米,斜边是5 厘米,这个三角形的面积是多少平方厘米?解题方法:直角三角形面积= 两条直角边乘积的一半,即3×4÷2 = 6(平方厘米)答案:6 平方厘米题目27:一个等腰三角形的周长是20 厘米,其中一条腰长8 厘米,底边长多少厘米?解题方法:等腰三角形两腰相等,所以底边长= 周长-腰长×2,即20 - 8×2 = 4(厘米)答案:4 厘米题目28:一个扇形的圆心角是90°,半径是6 厘米,这个扇形的面积是多少平方厘米?解题方法:扇形面积= 圆心角÷360°×圆的面积,即90÷360×3.14×6²= 28.26(平方厘米)答案:28.26 平方厘米题目29:一个长方体的底面是边长为5 厘米的正方形,高是8 厘米,这个长方体的体积是多少立方厘米?解题方法:长方体体积= 底面积×高,底面积= 5×5 = 25 平方厘米,体积= 25×8 = 200(立方厘米)答案:200 立方厘米题目30:一个圆柱的底面周长是18.84 厘米,高是10 厘米,它的体积是多少立方厘米?解题方法:底面半径= 18.84÷3.14÷2 = 3 厘米,体积= 3.14×3²×10 = 282.6(立方厘米)答案:282.6 立方厘米题目31:一个圆锥的底面直径是8 厘米,高是6 厘米,它的体积是多少立方厘米?解题方法:底面半径= 8÷2 = 4 厘米,体积= 1/3×3.14×4²×6 = 100.48(立方厘米)答案:100.48 立方厘米题目32:把一个棱长为8 厘米的正方体木块削成一个最大的圆柱,这个圆柱的体积是多少立方厘米?解题方法:圆柱的底面直径和高都是8 厘米,体积= 3.14×(8÷2)²×8 = 401.92(立方厘米)答案:401.92 立方厘米题目33:一个长方体玻璃缸,从里面量长4 分米,宽 3 分米,高5 分米,缸内水深2.5 分米。
几何图形综合1•如图,四边形ABCD 是直角梯形.其中AD=12(厘米),AB=8(厘米),BC=15(厘米),且△ ADE ,四边形DEBF ,△ CDF 的面积相等. 阴影△ DEF 的面积是多少平方厘米?2 .如图,长方形ABCD 的面积是96平方厘米,E 是AD 边上靠近D 点的三等 分点,F 是CD 边上靠近C 点的四等分点•阴影部分的面积是多少平方厘米?3. 如图,把一个正方形的两边分别增加 3和5厘米,结果面积增加了 71平方厘 米(阴影部分).原正方形的面积为多少平方厘米?4.如图,把一个正方形的相邻两边分别减少 2厘米和4厘米,结果面积减少了46平方厘米(阴影部分).原正方形的面积为多少平方厘米?5. 如图,在△ ABC 中,AD 的长度是AB 的四分之三,AE 的长度是 A AC 的三分之二.请问:△ ADE 的面积是厶ABC 面积的几分之几?「B J --------------------- ' C6. 如图,在△ ABC 中,BC=3CD , 是厶CDE 的多少倍?7. 如图,某公园的外轮廓是四边形 ABCD ,被对角线AC 、BD 分成四个部分• △ AOB 的面积是3平方千米,△ BOC 的面积是2平方千米,△ COD 的面积是1 平方千米,如果公园由大小为6. 9平方千米的陆地和一块人工湖组成, 那么人工AE DFCCFA EB湖的面积是多少平方千米?D9. 如图,有8个半径为1厘米的小圆,用它们圆周的一部分 连成一个花瓣图形,图中的黑点是这些圆的圆心 •如果圆周率 n 取3.14,那么花瓣图形的周长和面积分别是多少?10. 图中甲区域比乙区域的面积大 57平方厘米,且半圆的半径是 其中直角三角形竖直的直角边的长度是多少? ( n 取3.14)11. 如图,在3X 3的方格表中,分别以A 、E 为圆心,3、2为半径,画出圆心角都是90。
的两段圆弧.图中阴影部分的面积是多少?(12. 如图,求各图形中阴影部分的面积.(n 取3.14)13. 下图是一个直角边长为3厘米、4厘米的直角三角形.将该三角形一任意一条 边所在直线为轴进行旋转,求所得立体图形的表面积和体积 .8.如图,在梯形 ABCD 中,AD 长9厘米, BD 长12厘米,那么0D 长多少厘米?BC 长15厘米, A D10厘米. 甲L 814. 如图,已知正方形ABCD的边长为4厘米,求阴影部分的面积15. 斜边长为10厘米的等腰直角三角形的面积是多少?4 |21216. 右图中两个完全相同的三角形重叠在一起,则阴影部分的面积是多少?17. 求图中四边形的面积18. 图中八条边的长度正好分别是1,234,5,6,7,8厘米. 已知a=2厘米,b=4厘米,c=5厘米,求图形的面积.19. 如图所示,/ 1 + Z 2+Z 3+Z 4+ / 5+Z 6等于多少度?20. 如图,一个边长为1米的正方形被分成4个小长方形,它们的面积分别是 0.3 平方米、0. 4平方米、0.2平方米、0.1平方米.已知图中的 阴影部分是正方形,那么它的面积是多少平方米?21. 如图所示,三角形ABC 中, 求 AE: EC 及 DE: BC.22. 如图,红、黄、绿三块大小一样的正方形纸片,放在一个正方体盒内,,它们之 间相互重叠.已知露在外面的部分中,红色的面积是20,黄色的n 「 面积是14,绿色的面积是10.那么,正方体盒子的底面积是多少? _________ 黄L0. 3 ■0.4 0. 20. 1A23. 如图所示,已知△ ABC 的面积为1平方厘米, 是AB 、AC 边的中点.求三角形OBC 的面积.24. 在如图所示的正方形中,A 、B 、C 分别是ED 、EG 、 的中点.请问:△ CDO 的面积是厶ABO 面积的几倍?27. 如图,△ ABC 中,AD 、BE 相交于点 O ,A OAE 、△ OAB 、△ OBD 的面积分别为1、2、3,那么四边形ODCE 的面积多少?28. 图中有半径分别为5厘米、4厘米、3厘米的三个圆,部分)的面积与阴影部分的面积相比,哪个大?大多少?29.如图,图中最大的长方形面积是 27,最小的长方形面积是 面积.30. 阅读理解:⑴阅读:勾股定理是几何学中一颗光彩夺目的明珠,被称为“几何学的基石” , 中国是发现和研究勾股定理最古老的国家之一。
小学六年级奥数几何的初步知识精解1、长方形(1)特征对边相等,4个角都是直角的四边形。
有两条对称轴。
(2)计算公式 c=2(a+b) s=ab2、正方形(1)特征:四条边都相等,四个角都是直角的四边形。
有4条对称轴。
(2)计算公式:c=4a ;s=a??3、三角形(1)特征:由三条线段围成的图形。
内角和是180度。
三角形具有稳定性。
三角形有三条高。
(2)计算公式:s=ah/2(3)分类*按角分:锐角三角形:三个角都是锐角。
直角三角形:有一个角是直角。
等腰三角形的两个锐角各为45度,它有一条对称轴。
钝角三角形:有一个角是钝角。
*按边分:不等边三角形:三条边长度不相等。
等腰三角形:有两条边长度相等;两个底角相等;有一条对称轴。
等边三角形:三条边长度都相等;三个内角都是60度;有三条对称轴。
4、平行四边形(1)特征:两组对边分别平行的四边形。
相对的边平行且相等。
对角相等,相邻的两个角的度数之和为180度。
平行四边形容易变形。
(2)计算公式 s=ah5、梯形(1)特征:只有一组对边平行的四边形。
中位线等于上下底和的一半。
等腰梯形有一条对称轴。
(2)公式s=(a+b)h/2=mh6、圆(1)圆的认识平面上的一种曲线图形。
圆中心的一点叫做圆心。
一般用字母o表示。
半径:连接圆心和圆上任意一点的线段叫做半径。
一般用r表示。
在同一个圆里,有无数条半径,每条半径的长度都相等。
通过圆心并且两端都在圆上的线段叫做直径。
一般用d表示。
同一个圆里有无数条直径,所有的直径都相等。
同一个圆里,直径等于两个半径的长度,即d=2r。
圆的大小由半径决定。
圆有无数条对称轴。
(2)圆的画法把圆规的两脚分开,定好两脚间的距离(即半径);把有针尖的一只脚固定在一点(即圆心)上;把装有铅笔尖的一只脚旋转一周,就画出一个圆。
(3) 圆的周长围成圆的曲线的长叫做圆的周长。
把圆的周长和直径的比值叫做圆周率。
用字母∏表示。
(4) 圆的面积圆所占平面的大小叫做圆的面积。
几何部分题型大汇总1.-饨万秫醸懿分狐何长方臥护三个帼驰鼬擁詡分的郦2.⑦如右图”在长方形A BCD中「丹是正方形f已知二1%如「GC二九m ’则长方形卫弘刀的周长垦多厘米?知右图,在氏方^ADCD^ t山・G丿是工方腿,已知AA・10cf GC^7nn t则反方形丄此册周士磔附?3•如下图,两个相同的直角三角形重叠在一起,求阴影部分的面积是多少?4.四个相同的长方形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144,小正方形的面积是4,若用x、y表示长方形的长和宽,贝y小丄宽为长方形的长为第4题图5.三角形EDF的面积比三角形ABE的面积大6平方厘米,已知长方形ABCD勺长和宽分别为6、4厘米,DF长多少厘米?6•如图中三角形ABC被分成了甲(阴影部分)、乙两部分,BD=DC= 4,BE=2,EA=4,那么甲部分的面积是乙部分面积的几倍?7.如图,正方形ABCD的面积为3平方厘米,M是AD边上的中点,求阴影部分面积?8.有红黄蓝三块大小一样的正方形纸片,放在一个底面为正方形的盒,它们之间互相叠合.已知露在外面的部分中,红色面积是20. 黄色面积是14,绿色面积为10,求正方形盒底的面积。
9•如图,梯形ABCD的上底AD长为3厘米,下底BC长为9厘米•三角形ABO的面积为12平方厘米,则梯形ABCD的面积为多少?10.已知如图大正方形的边长是5厘米,小正方形的边长是3厘米,求阴影部分的面积?11.如图,三角形ABC的面积为1, BD : DC=2 : 1 , E是AC的中点, AD与BE相交于点P,那么四边形PDCE的面积为多少?B DC12.如图,一块长方形的布料ABCD,被剪成大小相等的甲、乙、丙、丁四块,其中甲块布料的长与宽的比为a:b=3 : 2,那么丁块布料的长与宽的比是_______ • 13.如图一块长方形铁皮,利用图中的阴影部分刚好能做成一个圆柱形油桶(接头处忽略不计).求油桶的容积?14.直角三角形ABC的三条边分别是5cm, 3cm和4cm,将它的直角边AC 对折到斜边AB上,使AC与AD重合,如下图,则图中阴影部分(未重叠部分)的面积是多少平方厘米?15.如图,已知直角三角形的面积是12平方厘米,求阴影部分面积.16.半径20厘米圆的外面和里面各有一个正方形,外面正方形的面积是多少,里面正方形的面积是多少?第16题第18题八炯罡由两衽罚腕来斯边卅别対耿和僱栄.硼謡盼匸角恤C)的酿是平方鳏・18.蛆大斯聊觸聽分是-个正?<嫌方蹦瞅是si19. 如下图,三角形ABC是等腰直角三角形,一直角边长为4厘米,求阴影部分的面积?20. 已知下图平行四边形的面积是36平方厘米,求图中阴影部分面积要求写出计算过。
小学六年级奥数知识:几何初步认识(平面图形)这篇关于小学六年级奥数知识:几何初步认识(平面图形),是特地为大家整理的,希望对大家有所帮助!二、平面图形1、长方形(1)特征对边相等,4个角都是直角的四边形。
有两条对称轴。
(2)计算公式c=2(a+b)s=ab2、正方形(1)特征:四条边都相等,四个角都是直角的四边形。
有4条对称轴。
(2)计算公式c=4as=a23、三角形(1)特征由三条线段围成的图形。
内角和是180度。
三角形具有稳定性。
三角形有三条高。
(2)计算公式s=ah/2(3)分类按角分锐角三角形:三个角都是锐角。
直角三角形:有一个角是直角。
等腰三角形的两个锐角各为45度,它有一条对称轴。
钝角三角形:有一个角是钝角。
按边分不等边三角形:三条边长度不相等。
等腰三角形:有两条边长度相等;两个底角相等;有一条对称轴。
等边三角形:三条边长度都相等;三个内角都是60度;有三条对称轴。
4、平行四边形(1)特征两组对边分别平行的四边形。
相对的边平行且相等。
对角相等,相邻的两个角的度数之和为180度。
平行四边形容易变形。
(2)计算公式s=ah5、梯形(1)特征只有一组对边平行的四边形。
中位线等于上下底和的一半。
等腰梯形有一条对称轴。
(2)公式s=(a+b)h/2=mh6、圆(1)圆的认识平面上的一种曲线图形。
圆中心的一点叫做圆心。
一般用字母o 表示。
半径:连接圆心和圆上任意一点的线段叫做半径。
一般用r表示。
在同一个圆里,有无数条半径,每条半径的长度都相等。
直径:通过圆心并且两端都在圆上的线段叫做直径。
一般用d表示。
同一个圆里有无数条直径,所有的直径都相等。
同一个圆里,直径等于两个半径的长度,即d=2r。
圆的大小由半径决定。
圆有无数条对称轴。
(2)圆的画法把圆规的两脚分开,定好两脚间的距离(即半径);把有针尖的一只脚固定在一点(即圆心)上;把装有铅笔尖的一只脚旋转一周,就画出一个圆。
(3)圆的周长围成圆的曲线的长叫做圆的周长。
小学奥数——几何图形一.选择题(共50小题)1.图中的八边形是将大长方形纸片剪去一个小长方形得到.则至少需要知道()条线段的长度,才可以计算出这个八边形的周长.A.4B.3C.5D.102.如图中阴影部分是正方形,最大长方形的周长是()厘米.A.22B.26C.36D.无法确定3.如图,由6个边长为3厘米的小正方形拼成的图形,它的周长是()厘米.A.36B.39C.42D.454.把一个直径是4厘米的圆分成两个完全相等的半圆,这两个半圆的周长之和是()A.12.56厘米B.16.56厘米C.20.56厘米D.24.56厘米5.如图,有8条线段,至少要分别测量编号为()的三条线段的长度,才能求出这个图形的周长.A.①②⑤B.①②③C.①②⑦D.②③⑦6.如图,是一个台阶的侧面(线段AC,BC,AB的长依次为5米、12米、13米)要在台阶上面铺上红地毯,且上下各多铺出两米,需要地毯的长度是()米.A.17B.18C.20D.217.如图,正方形被一条曲线分成了A、B两部分,下面第()种说法不正确?A.如果a>b,那么A的周长大于B的周长B.如果a<b,那么A的周长小于B的周长C.如果a=b,那么A的周长等于B的周长D.不管a、b哪个大,A、B的周长总是相等8.如图是用3个长8厘米、宽3厘米的长方形拼成的,这个图形的周长是()A.66厘米B.48厘米C.45厘米2C.489.图中多边形每相邻两条边都互相垂直,若要计算起其周长,那么至少要知道()边长.A.6B.5C.4D.310.一个长方形花园长是30米,宽是10米,沿着花园走两圈,共走了()A.45米B.90米C.160米D.200米11.把如图的长方形用一条曲线分成甲、乙两个图形,甲图与乙图的周长相比,()A.甲图的长B.乙图的长C.甲图与乙图同样长12.如图,在由1⨯1的正方形组成的网格中写有2015四个数字(阴影部分),其边线要么是水平或竖直的直线段,要么是连接1⨯1的正方形相邻两边中点的线段,或者是1⨯1的正方形的对角线,则图中2015四个数字(阴影部分)的面积是()A.47B.471 D.481213.如图中,正八边形ABCDEFGH的面积为1,其中有两个正方形ACEG和PQRS.那么正八边形中阴影部分的面积()2B.A.123C.35D.5814.如图,大正方形的边长为14,小正方形的边长为10,阴影部分的面积之和是()A.25B.40C.49D.5015.大、中、小三个正方形,边长都是整数厘米,小正方形的周长比中正方形的边长小,把这两个正方形放在大正方形上(如图),大正方形露出的部分的面积是10平方厘米(图中阴影部分).那么,大正方形的面积是()平方厘米.A.25B.36C.49D.6416.如图,大正六边形内部有7个完全一样的小正六边形,已知阴影部分的面积是180平方厘米.那么大正六边形的面积是()平方厘米.A.240B.270C.300D.36017.如图所示,在58的方格中,阴影部分的面积为37cm2.则非阴影部分的面积为()cm2.lA.43B.74C.80D.11118.图中,将两个正方形放在一起,大、小正方形的边长分别为0,6,则图中阴影部分面积为()A.42B.40C.38D.3619.下图中,四边形ABCD都是边长为1的正方形,E、F、G、H分别是AB、BC、CD、DA的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数m n的值等于()mn,那么,A.5B.7C.8D.1220.有5个长方形,它们的长和宽都是整数,且5个长和5个宽恰好是1~10这10个整数;现在用这5个长方形拼成1个大正方形,那么,大正方形面积的最小值为()A.169B.144C.121D.10021.一个梯形的上底增加2厘米,下底减少2厘米,高不变,它的面积与原面积相比()A.变大了C.不变B.变小了D.高不知道,所以无法比较22.已知图中正方形的两个顶点正好是两个等腰直角三角形斜边上的中点,小等腰直角三角形与正方形中的圆面积相等,请问正方形中的阴影面积与大等腰直角三角形面积的比值3B.2C.1是()A.11 D.3223.如图,梯形ABCD中,AB//D C,∠ADC+∠BCD=90︒,且DC=2A B,分别以DA、AB、BC为边向梯形外作正方形,其面积分别为S,S,S,则S,S,S之间的关系是下123123列选项中的()A.S+S>S;B.S+S=S;C.S+S<S;D.无法确定.12313213224.小王将一些同样大小的正三角形纸片摆放在桌上.第一次放1张纸片;第二次在这个小正三角形纸片四周再放三张纸片;第三次在第二次摆好的图形四周再摆放纸片;⋯摆放要求是:每次摆放的每张纸片必须和上一次摆放的纸片至少有一条边重合,且纸片之间除边之外,无重合(见图).第20次摆放后,该图形共用了正三角形纸片()张.A.571B.572C.573D.57425.在8⨯8网格的所有方格中放入黑白两种围棋子,每个方格放一枚棋子,要求每行中的白色棋子的数目互不相同,每列中的白色棋子的数目相等,那么这个8⨯8网格中共有( )枚黑色棋子.A.42B.32C.22D.1226.在6⨯6网格的所有方格中放入围棋子,每个方格放1枚棋子,要求每行中的白色棋子的数目互不相等,每列中的白色棋子的数目都相等,那么这个6⨯6网格中共有()枚黑.色围棋子.A.18B.14C.12D.1027.一块木板上有13枚钉子(如图1所示)用橡皮筋套住其中的几枚钉子,可以构成三角形,正方形,梯形等等(如图2).请回答:可以构成()个正方形.A.9B.10C.11D.1228.在如图中,一共能数出()个含有“☆”的长方形.A.8B.10C.12D.1429.如图,木板上有10根钉子,任意相邻的两根钉子距离都相等,以这些钉子为顶点,用橡皮筋可套出()个正三角形.A.6B.10C.13D.1530.以平面上任意4个点为顶点的三角形中,钝角三角形最多有()个.A.5B.2C.4D.331.图中,有()个三角形.A.13B.15C.14D.1632.图中共有()个三角形.A.10B.9C.19D.1833.两个小三角形不重叠放置可以拼成一个大三角形,那么这个大三角形不可能由()拼成.A.两个锐角三角形B.两个直角三角形C.两个钝角三角形D.一个锐角三角形和一个钝角三角形34.将长方形ABCD对角线平均分成12段,连接成如图,长方形ABCD内部空白部分面积总和是10平方厘米,那么阴影部分面积总和是()平方厘米.A.14B.16C.18D.2035.在桌面上,将一个边长为1的正六边形纸片与一个边长为1的正三角形纸片拼接,要求无重叠,且拼接的边完全重合,则得到的新图形的边数为()A.8B.7C.6D.536.用210个大小相同的正方形拼成一个长方形,不同的拼法有()种.A.2B.4C.6D.837.一个长方形由15个小正方形拼成,如图所示,若这个长方形的周长是64cm,则它的面积为()cm2.A.960B.256C.240D.12838.如图,每条边都相等,每个角都是直角,则根据信息,求下图的面积为)平方厘米.(A.16B.20C.24D.3239.如图,四边形ABCD为长方形,四边形CDEF为平行四边形.下面四种说法中正确的是()A.甲的面积比乙的面积大B.甲的面积比乙的面积小C.只有当丙、丁两部分面积相等时,甲、乙两部分面积才相等D.甲、乙两部分面积总是相等的,与丙、丁两部分面积的大小无关40.如图,正方形ABCD的边长是10厘米,长方形EFGH的长为8厘米,宽为5厘米.则阴影部分的甲与阴影部分乙面积的差是()平方厘米.A.40B.50C.60D.8041.如图,线段BE将长方形ABCD分成M、N两个部分,如果M部分比N部分的面积小l80平方厘米,那么AE的长是()A.24厘米B.21厘米C.20厘米D.14厘米42.如图,一个33的正方形网格,如果小正方形边长是1,那么阴影部分的面积是()A.5B.4C.3D.243.如图所示,四边形BCDE为平行四边形,∆AOE的面积为6,求∆BOC的面积.()A.3B.4C.5D.644.如图,M为平行四边形ABCD的边BC上的一点,且BM:MC=2:3,已知三角形C MN的面积为45cm2,则平行四边形ABCD的面积为()cm2.A.30B.45C.90D.10045.如图,长方形ABCD中的AE、AF、AG、AH四条线段把此长方形面积五等分,又长等于()平方厘米.方形长20厘米、宽12厘米,那么三角形AFG的面积S∆AFGA.41.2B.43.2C.43.1D.42.346.在等腰梯形ABCD中,AB平行于CD,AB=6,CD=14,∠AEC是直角,CE=CB,则AE2等于()A.84B.80C.75D.6447.下面的四个图形中,第()幅图只有2条对称轴.A. B.C. D.48.下面图形中,恰有2条对称轴()A. B. C. D.49.在如图的阴影三角形中,不能由右图中的阴影三角形经过旋转、平移得到的是图(的三角形.)中A. B.C. D.50.在下面的阴影三角形中,不能由图中的阴影三角形经过旋转、平移得到的是图(的三角形.)中A. B. C. D.参考答案与试题解析一.选择题(共50小题)1.图中的八边形是将大长方形纸片剪去一个小长方形得到.则至少需要知道()条线段的长度,才可以计算出这个八边形的周长.A.4B.3C.5【解析】如上图,把线段①平移到②的位置可以组成一个大长方形,大长方形的4条边,对边相等,所以只需知道相邻两条边的长度,③=④,所以只需知道1条线段的长度,所以求八边形的周长需要知道:2+1=3条线段的长度.故选:B.2.如图中阴影部分是正方形,最大长方形的周长是()厘米.D.10A.22B.26C.36【解析】(9+4)⨯2=26答:最大长方形的周长是26厘米.3.如图,由6个边长为3厘米的小正方形拼成的图形,它的周长是(D.无法确定)厘米.A.36B.39C.42D.45【解析】3⨯4=12(厘米)3⨯2=6(厘米)(12+6)⨯2+6=36+6=42(厘米)答:它的周长是42厘米.故选:C.4.把一个直径是4厘米的圆分成两个完全相等的半圆,这两个半圆的周长之和是()A.12.56厘米B.16.56厘米C.20.56厘米D.24.56厘米【解析】(3.14⨯4÷2+4)⨯2=(6.28+4)⨯2=10.28⨯2=20.56(厘米)答:这两个半圆周长之和是20.56厘米.故选:C.5.如图,有8条线段,至少要分别测量编号为()的三条线段的长度,才能求出这个图形的周长.A.①②⑤B.①②③C.①②⑦D.②③⑦【解析】由图形可知,④+⑥的线段补给⑧所在的长方形边的虚线部分,⑦-⑤等长线段的补给③所在边的虚线部分,这样就构成了一个完整的长方形,原图形的周长就是答长方形的周长+2个⑤的线段总长,所以图形的周长只要知道①②⑤即可求得.故选:A.6.如图,是一个台阶的侧面(线段AC,BC,AB的长依次为5米、12米、13米)要在台阶上面铺上红地毯,且上下各多铺出两米,需要地毯的长度是()米.A.17B.18C.20D.21【解析】12+5+2⨯2=12+5+4=21(米)答:需要地毯的长度是21米.故选:D.7.如图,正方形被一条曲线分成了A、B两部分,下面第()种说法不正确?A.如果a>b,那么A的周长大于B的周长B.如果a<b,那么A的周长小于B的周长C.如果a=b,那么A的周长等于B的周长D.不管a、b哪个大,A、B的周长总是相等【解析】A的周长=曲线长+正方形边长⨯2+b-aB的周长=曲线长+正方形边长⨯2+a-b所以A、B、C选项都是正确的,错误的是D.8.如图是用3个长8厘米、宽3厘米的长方形拼成的,这个图形的周长是()22A.66厘米B.48厘米C.45厘米【解析】8⨯6-3⨯1=48-3=45(厘米)答:这个图形的周长是45厘米.故选:C.9.图中多边形每相邻两条边都互相垂直,若要计算起其周长,那么至少要知道()边长.A.6B.5C.4D.3【解析】根据题干分析可得:这个图形的横着的边长之和是:b;竖着的边长之和是:a+2c;所以这个图形的周长是:2a+2b+2c=2(a+b+c),故计算这个图形的周长至少需要知道3条边,故选:D.10.一个长方形花园长是30米,宽是10米,沿着花园走两圈,共走了()A.45米B.90米C.160米D.200米【解析】(30+10)⨯2⨯2=160(米)故选:C.11.把如图的长方形用一条曲线分成甲、乙两个图形,甲图与乙图的周长相比,()A.甲图的长C.甲图与乙图同样长【解析】B.乙图的长2C.482B.因为,甲图形的周长是:AB+BC+AC,乙图形的周长是:DC+AD+AC,而AB=CD,AD=BC,所以,甲、乙两个图形的周长相等;故选:C.12.如图,在由1⨯1的正方形组成的网格中写有2015四个数字(阴影部分),其边线要么是水平或竖直的直线段,要么是连接1⨯1的正方形相邻两边中点的线段,或者是1⨯1的正方形的对角线,则图中2015四个数字(阴影部分)的面积是()A.47B.471D.4812【解析】据分析可知:将小三角形移到空白处补全完整正方形,共47.5个,所以阴影部分的面积是4712;故选:B.13.如图中,正八边形ABCDEFGH的面积为1,其中有两个正方形ACEG和PQRS.那么正八边形中阴影部分的面积()A.123C.35D.58【解析】根据分析,将图中阴影部分进行等积变形,由图不难发现,阴影部分和空白部分的面积刚好相等,正八边形中阴影部分的面积占:1 2故选:A.14.如图,大正方形的边长为14,小正方形的边长为10,阴影部分的面积之和是()A.25B.40C.49D.50【解析】根据分析,如下图所示,图①逆时针旋转90︒,阴影部分可拼成一等腰直角三角形,S=142÷4=49故选:C.15.大、中、小三个正方形,边长都是整数厘米,小正方形的周长比中正方形的边长小,把这两个正方形放在大正方形上(如图),大正方形露出的部分的面积是10平方厘米(图中阴影部分).那么,大正方形的面积是()平方厘米.A.25B.36C.49D.64【解析】根据分析,一条阴影部分的面积为10÷2=5平方厘米.因为都是整数,所以只能为1⨯5.故,大正方形面积=(1+5)⨯(1+5)=6⨯6=36平方厘米.故选:B.16.如图,大正六边形内部有7个完全一样的小正六边形,已知阴影部分的面积是180平方厘米.那么大正六边形的面积是()平方厘米.A.240B.270C.300D.360【解析】如图所示,将图分割成面积相等的小正三角形,显然,图中的空白部分的面积和等于3个小正六边形.而阴影部分由6个小正六边形组成,所以,大正六边形是由9个小正六边形组成的.一个小正六边形的面积为:180÷6=30(平方厘米),大正六边形的面积为:30⨯9=270(平方厘米),故选:B.l17.如图所示,在 5 ⨯ 8 的方格中,阴影部分的面积为 37cm 2 .则非阴影部分的面积为 ()cm 2 .A.43【解析】如图,B.74C.80 D .111阴影部分占了 18.5 个格,面积为 37cm 2 ,每格的面积是: 37 ÷ 18.5 = 2(cm 2 ) ;非阴影就分占 21.5 格,其面积是: 21.5 ⨯ 2 = 43(cm 2 ) ; 答:则非阴影部分的面积为 43cm 2 ;故选: A .18.图中,将两个正方形放在一起,大、小正方形的边长分别为 0 ,6,则图中阴影部分面积为 ()A.42B.40C.38D .36【解析】10 ⨯10 + 6 ⨯ 6 - 6 ⨯ (10 + 6) ÷ 2 - 10 ⨯10 ÷ 2= 100 + 36 - 48 - 50【解析】由以上可知,两个阴影面积比为 : = 3: 2 ,= 38答:阴影部分的面积是 38.故选: C .19.下图中,四边形 ABCD 都是边长为 1 的正方形,E 、F 、G 、H 分别是 AB 、BC 、CD 、DA 的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数m + n 的值等于 ()mn,那么,A.5B.7C.8 D .121 12 33 + 2 = 5.故选: A .20.有 5 个长方形,它们的长和宽都是整数,且 5 个长和 5 个宽恰好是1~10 这 10 个整数;现在用这 5 个长方形拼成 1 个大正方形,那么,大正方形面积的最小值为()A.169【解析】如图所示,B.144C.121 D .100,于是可得:正方形的边长为 11,则其面积为11⨯11 = 121.答:大正方形面积的最小值为 121.故选: C .3B. 2C.1则正方形的面积是 ( )2 + ( )2 = + =小等腰三角形与大等腰三角形的面积和: + =21.一个梯形的上底增加 2 厘米,下底减少 2 厘米,高不变,它的面积与原面积相比 ()A.变大了C.不变B.变小了D.高不知道,所以无法比较【解析】因为梯形的面积 = (上底 + 下底) ⨯ 高 ÷2 ,若“上底增加 2 厘米,下底减少 2 厘米,高不变”则(上底 + 下底)的和不变,且高不变,所以梯形的面积不变.故选: C .22.已知图中正方形的两个顶点正好是两个等腰直角三角形斜边上的中点,小等腰直角三角形与正方形中的圆面积相等,请问正方形中的阴影面积与大等腰直角三角形面积的比值是 ()A.1 1D.32【解析】设小等腰三角形的边长是 a ,大等腰三角形的边长为 b , 则小三角形的斜边是 2a ,大三角形的斜边为 2b2a 2b a 2 b 2 a 2 + b 22 2 2 2 2a 2b 2 a 2 + b 22 2 2又因小等腰直角三角形与正方形中的圆面积相等,所以正方形中的阴影面积与大等腰直角三角形面积相等.所以它们的比值是 1.故选: C .23.如图,梯形 ABCD 中,AB / / D C ,∠ADC + ∠BCD = 90︒ ,且 DC = 2 A B ,分别以 DA 、AB 、BC 为边向梯形外作正方形,其面积分别为S , S , S ,则 S , S , S 之间的关系是下12 3 1 2 3列选项中的 ()A.S+S>S;B.S+S=S;C.S+S<S;D.无法确定.123132132【解析】过点A作AE//BC交CD于点E,因为AB//D C,所以四边形AECB是平行四边形,所以AB=CE,BC=AE,∠BCD=∠AED,因为∠ADC+∠BCD=90︒,DC=2A B,所以AB=DE,∠ADC+∠AED=90︒,所以∠DAE=90︒那么AD2+AE2=DE2,因为S=AD2,S=AB2=DE2,S=BC2=AE2,123所以S=S+S.213故选:B.24.小王将一些同样大小的正三角形纸片摆放在桌上.第一次放1张纸片;第二次在这个小正三角形纸片四周再放三张纸片;第三次在第二次摆好的图形四周再摆放纸片;⋯摆放要求是:每次摆放的每张纸片必须和上一次摆放的纸片至少有一条边重合,且纸片之间除边之外,无重合(见图).第20次摆放后,该图形共用了正三角形纸片()张.A.571B.572C.573D.574【解析】根据分析可得,.第 20 次摆放后,该图形共用:1 + 3 + 6 + 9 +⋯+ 3 ⨯ (20 - 1)= 1 + 3 + 6 + 9 +⋯+ 57= (3 + 57) ⨯ (20 - 1) ÷ 2 + 1= 570 + 1= 571 (个 )答:第 20 次摆放后,该图形共用了正三角形纸片 571 张.故选: A .25.在 8 ⨯ 8 网格的所有方格中放入黑白两种围棋子,每个方格放一枚棋子,要求每行中的白色棋子的数目互不相同,每列中的白色棋子的数目相等,那么这个8 ⨯ 8 网格中共有 () 枚黑色棋子.A.42B.32C.22 D .12【解析】由分析得0 + 1 + 2 + 3 + 5 + 6 + 7 + 8 = 32 (枚 )8 ⨯ 8 - 32 = 32 (枚 )故选: B .26.在 6 ⨯ 6 网格的所有方格中放入围棋子,每个方格放 1 枚棋子,要求每行中的白色棋子的数目互不相等,每列中的白色棋子的数目都相等,那么这个 6 ⨯ 6 网格中共有 () 枚黑色围棋子.A.18B.14C.12 D .10【解析】每行的数目可以为 0 ~ 6 个,每列都相等,所以一定是 6 的倍数,0 + 1 + 2 + 3 + 4 + 5 + 6 = 21 ,如果去掉 3,那么剩下的数: 21 - 3 = 18 正好是 6 的倍数,所以,白棋子有 18 个,则,黑色围棋子有: 6 ⨯ 6 - 18 = 18 (个 )故选: A .27.一块木板上有 13 枚钉子(如图 1 所示)用橡皮筋套住其中的几枚钉子,可以构成三角形,正方形,梯形等等(如图 2) .请回答:可以构成 () 个正方形.A.9【解析】B.10C.11D.12第一种正方形有5个,第二种正方形有4个,第三个正方形有1个,第四种正方形有1个,共11个.故选:C.28.在如图中,一共能数出()个含有“☆”的长方形.A.8B.10C.12D.14【解析】根据分析可得,共有:6+6=12(个);答:图中,一共能数出12个含有“☆”的长方形.故选:C.29.如图,木板上有10根钉子,任意相邻的两根钉子距离都相等,以这些钉子为顶点,用橡皮筋可套出()个正三角形.A.6B.10C.13D.15【解析】单个的三角形有9个,4个三角形组成的大三角形3个,最外面的最大的三角形1个,共有:9+3+1=13(个)答:用橡皮筋可套出13个正三角形.故选:C.30.以平面上任意4个点为顶点的三角形中,钝角三角形最多有()个.A.5B.2C.4D.3【解析】如图,平面上任意4点构成了4个钝角三角形:∆ABC、∆ABD、∆ACD、∆BCD,所以以平面上任意4个点为顶点的三角形中,钝角三角形最多有4个.故选:C.31.图中,有()个三角形.A.13B.15C.14D.16【解析】由题意,由一个小三角形构成的,有6个;由两个小三角形构成的,有3个;由三个小三角形构成的,有6个;大三角形1个,所以三角形的个数为6+3+6+1=16个,故选:D.32.图中共有()个三角形.A.10B.9C.19D.18而实际空白部分面积总和是 10 平方厘米,可得单位 1 的实际面积是10 ÷ 15 = (平方厘米);【解析】根据题干分析可得:8 + 8 + 2 = 18 (个 ) ,答:图中一共有 18 个三角形.故选: D .33.两个小三角形不重叠放置可以拼成一个大三角形,那么这个大三角形不可能由() 拼成.A.两个锐角三角形B.两个直角三角形C.两个钝角三角形D.一个锐角三角形和一个钝角三角形【解析】因为拼在一起的两个小三角形一定有两条边共线,这时能组成一个平角,A 、因为两个锐角的和小于 180 度,所以,两个锐角三角形不可能拼成一个大三角形;B 、因为 90︒ + 90︒ = 180︒ ,所以两个直角三角形能拼成一个大三角形;C 、因为钝角 + 锐角有可能等于180︒ ,所以两个钝角三角形可能拼成一个大三角形;D 、因为钝角 + 锐角有可能等于180︒ ,所以两个钝角三角形可能拼成一个大三角形;故选: A .34.将长方形 ABCD 对角线平均分成 12 段,连接成如图,长方形 ABCD 内部空白部分面积总和是 10 平方厘米,那么阴影部分面积总和是() 平方厘米.A.14B.16C.18 D .20【解析】设把中间最小的空白长方形的面积看作单位1 = ab ,那么与它相邻的阴影部分的面积就是 2a ⨯ 2b - ab = 3ab = 3 ,同理,相邻的空白部分的面积就是 5ab = 5 ,依此规律,面积依次下去为 7,9,11,则空白部分的面积总和是1 + 5 + 9 = 15 ,23那么阴影部分面积总和是: 3 + 7 + 11 = 21 ,;则实际面积是:21⨯23=14(平方厘米)答:阴影部分面积总和是14平方厘米.故选:A.35.在桌面上,将一个边长为1的正六边形纸片与一个边长为1的正三角形纸片拼接,要求无重叠,且拼接的边完全重合,则得到的新图形的边数为()A.8B.7C.6D.5【解析】180︒⨯(6-2)÷6=180︒⨯4÷6=120︒180︒÷6=60︒120︒+60︒=180︒所以,拼接后的图形是:6+3-4=5(条)答:得到的新图形的边数为5.故选:D.36.用210个大小相同的正方形拼成一个长方形,不同的拼法有()种.A.2B.4C.6D.8【解析】210=2⨯3⨯5⨯7因数的总个数:(1+1)⨯(1+1)⨯(1+1)⨯(1+1)=16(个)不同的拼法有:16÷2=8(种)答:不同的拼法有8种.故选:D.37.一个长方形由15个小正方形拼成,如图所示,若这个长方形的周长是64cm,则它的面积为()cm2.(A.960B.256C.240D.128【解析】64÷[(5+3)⨯2]=64÷16=4(厘米)4⨯4⨯15=240(平方厘米)答:它的面积为240cm2.故选:C.38.如图,每条边都相等,每个角都是直角,则根据信息,求下图的面积为)平方厘米.A.16B.20C.24D.32【解析】如右图进行分割,把图形分成了8个边长是2厘米的小正方形2⨯2⨯8=32(平方厘米)答:这个图形的面积是32平方厘米.故选:D.39.如图,四边形ABCD为长方形,四边形CDEF为平行四边形.下面四种说法中正确的是()A.甲的面积比乙的面积大B.甲的面积比乙的面积小C.只有当丙、丁两部分面积相等时,甲、乙两部分面积才相等D.甲、乙两部分面积总是相等的,与丙、丁两部分面积的大小无关【解析】四边形ABCD为长方形,所以BC=AD,AB=CD,因为四边形CDEF为平行四边形,所以C D=EF,所以AB=EF,两边同时加上BE,所以BF=AE;根据等底等高的三角形的面积相等,所以得出三角形CBF的面积=三角形DAE的面积,则:三角形CBF的面积-丁的面积=三角形DAE的面积-丁的面积,所以甲、乙两部分面积总是相等,与与丙、丁两部分面积的大小无关;故选:D.40.如图,正方形ABCD的边长是10厘米,长方形EFGH的长为8厘米,宽为5厘米.则阴影部分的甲与阴影部分乙面积的差是()平方厘米.A.40B.50C.60D.80【解析】10⨯10-8⨯5=60(平方厘米)故选:C.41.如图,线段BE将长方形ABCD分成M、N两个部分,如果M部分比N部分的面积小l80平方厘米,那么AE的长是()A.24厘米B.21厘米C.20厘米D.14厘米【解析】设N部分的面积为x,那么M部分的面积为x-180,x+(x-180)=30⨯202x-180=600;2x=600+1802x=780x=390;N部分的面积是390平方厘米.设梯形的上底为y,(y+30)⨯20⨯1=390210y+300=39010y=90y=9;AE=30-9=21(厘米)故选:B.42.如图,一个3⨯3的正方形网格,如果小正方形边长是1,那么阴影部分的面积是()A.5B.4C.3D.2【解析】通过观察可知,阴影部分的面积=长是3宽是1的长方形的面积-中间边长是1的正方形的面积.3⨯1-1⨯1=2故选:D.43.如图所示,四边形BCDE为平行四边形,∆AOE的面积为6,求∆BOC的面积.()A.3【解析】连接BD,B.4C.5D.6因为,BE//CD,OB=OB,所以,∆BOC的面积等于∆BOD的面积,又因为,DE//AC,AB=AB,所以,∆ABE的面积等于∆ABD的面积,又因为,∆ABO是∆ABE和∆ABD的公共部分,所以,∆BOD的面积等于∆AOE的面积,即,∆BOD的面积=∆AOE的面积=6.答:∆BOC的面积是6.故选:D.44.如图,M为平行四边形ABCD的边BC上的一点,且BM:MC=2:3,已知三角形C MN的面积为45cm2,则平行四边形ABCD的面积为()cm2.A.30B.45C.90D.100【解析】如图,连接AC.Q四边形ABCD是平行四边形,∴AD//B N,∴∆A DM∽∆NCM,)2 = ,= S∴ S∆ADM = (S∆MNCDM 4CM 9Q S∴ S∆MNC ∆ADM= 45 ,= 20 ,Q CM : DM = 3: 2 ,∴ S∴ S∴ S = 30 , ∆ACM= 50 ,∆ADC平行四边形ABCD= 2S∆ADC= 100 ,故选: D .45.如图,长方形 ABCD 中的 AE 、 AF 、 AG 、 AH 四条线段把此长方形面积五等分,又长方形长 20 厘米、宽 12 厘米,那么三角形 AFG 的面积 S∆AFG等于 ( ) 平方厘米.A.41.2B.43.2C.43.1D .42.3【解析】由题意可知 S∆ABE= S∆AEF= S∆AGH= S∆ADH=20 ⨯125= 48 ,∴ B E = EF , DH = HG ,Q 1g BE g AB = 48 ,2∴ BE = EF = 8 , CF = 20 - 16 = 4 ,Q 1g DH g AD = 48 ,2∴ DH = HG = 4.8 , CG = 2.4 ,∴ S 1 2∴ S∆AFG= 48- 4.8 = 43.2 ,故选: B .46.在等腰梯形ABCD中,AB平行于CD,AB=6,CD=14,∠AEC是直角,CE=CB,则AE2等于()A.84【解析】如图,B.80C.75D.64连接AC,过点A作AF⊥CD于点F,过点B作BG⊥CD于点G,则AF=BG,AB=FG=6,DF=CG=4.在直角∆AFC中,AC2=AF2+FC2=AF2+102=AF2+100,在直角∆BGC中,BC2=BG2+GC2=AF2+42=AF2+16,又Q CE=CB,∠AEC=90︒,∴AE2=AC2-EC2=AF2+100-(A F2+16)=84,即AE2=84.故选:A.47.下面的四个图形中,第()幅图只有2条对称轴.A. B.C. D.【解析】如果沿某条直线对折,对折的两部分是完全重合的,那么就称这样的图形为轴对称图形,这条直线叫做这个图形的对称轴.观察易知,符合题意的是C.故选:C.48.下面图形中,恰有2条对称轴()A. B. C. D.【解析】根据轴对称图形的定义,可得:A有4条对称轴,B没有对称轴,C有2条对称轴,D有1条对称轴.故选:C.49.在如图的阴影三角形中,不能由右图中的阴影三角形经过旋转、平移得到的是图()中的三角形.A. B.C. D.【解析】根据分析,可以逆向思维,可以将题中的阴影三角形经过旋转、平移,长直角边旋转和短直角边旋转后得到的图形,不难看出,只有A选项是不可能出现的.图中图中①、②、③三边应为顺时针关系,A不合要求.故选:A.50.在下面的阴影三角形中,不能由图中的阴影三角形经过旋转、平移得到的是图()中的三角形.A. B. C. D.【解析】解析:由图可知:A、C、D都可由原三角形经过旋转和平移得到,而B选项必须经过对称才能与原三角形重合,故选:B.。
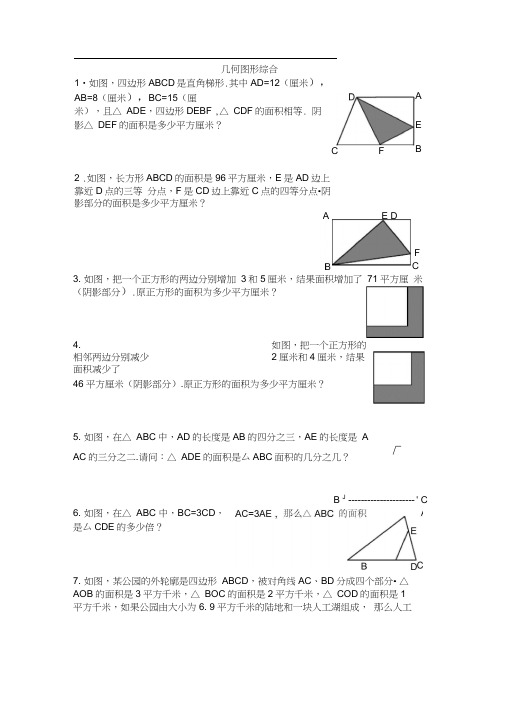
几何图形综合
1.如图,四边形ABCD 是直角梯形.其中AD=12(厘米),AB=8(厘米),BC=15(厘米),且△ADE ,四边形DEBF ,△CDF 的面积相等. 阴影△DEF 的面积是多少平方厘米?
2.如图,长方形ABCD 的面积是96
平方厘米,E 是AD 边上靠近
D 点的三等分点,F 是CD 边上靠近C 点的四等分点.阴影部分的面积是多少平方厘米?
3.如图,把一个正方形的两边分别增加3和5厘米,米(阴影部分).原正方形的面积为多少平方厘米?
4.如图,把一个正方形的相邻两边分别减少2厘米和446平方厘米(阴影部分).原正方形的面积为多少平方厘米?
5.如图,在△ABC 中,AD 的长度是AB 的四分之三,AE 的长度是 AC 的三分之二.请问:△ADE 的面积是△ABC 面积的几分之几?
6.如图,在△ABC 中,BC=3CD ,AC=3AE ,那么△ABC 的面积
是△CDE 的多少倍?
7.如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分.△AOB 的面积是3平方千米,△BOC 的面积是2平方千米,△COD 的面积是1平方千米,如果公园由大小为6.9平方千米的陆地和一块人工湖组成,那么人工
湖的面积是多少平方千米?
E D
F B C
A D E A
B C
E A D
8.如图,在梯形ABCD 中,AD 长9厘米,BC 长15厘米, BD 长12厘米,那么OD 长多少厘米? 9.如图,有8个半径为1厘米的小圆,用它们圆周的一部分 连成一个花瓣图形,图中的黑点是这些圆的圆心.如果圆周率 π取3.14,那么花瓣图形的周长和面积分别是多少? 10.图中甲区域比乙区域的面积大57
其中直角三角形竖直的直角边的长度是多少?(π取3.14) 11.如图,在3×3的方格表中,分别以A 、E 为圆心,3、2为半径,画出圆心角都是90º的两段圆弧.图中阴影部分的面积是多少? (π取3
.14)
.(π取
13.下图是一个直角边长为3厘米、
4厘米的直角三角形.将该三角形一任意一条边所在直线为轴进行旋转,求所得立体图形的表面积和体积.
14.如图,已知正方形ABCD 的边长为4厘米,求阴影部分的面积.
A D O
B C
● ● ●
● ● ●
● ● ● ● ● ● ● ● ●
a b
c d e f h
g
15.斜边长为10厘米的等腰直角三角形的面积是多少?
16.右图中两个完全相同的三角形重叠在一起,则阴影部分的面积是多少?
17.求图中四边形的面积.
18.图中八条边的长度正好分别是1,2,3,4,5,6,7,8厘米. 已知a =2厘米,b
=4厘米,c =5厘米,求图形的面积.
19.如图所示,∠1+∠2+∠3+∠4+∠5+
∠6等于多少度?
20.如图,一个边长为1米的正方形被分成4个小长方形,它们的面积分别是0.3平方米、0.4平方米、0.2平方米、0.1平方米. 已知图中的
阴影部分是正方形,那么它的面积是多少平方米?
21.如图所示,三角形ABC 中,DE 与BC 平行,且AD :DB=5求AE :EC 及DE :BC .
22.如图,间相互重叠.已知露在外面的部分中,红色的面积是20,黄色的
面积是14,绿色的面积是10.那么,
B A D 1 2 3 4 5 6 绿
23.如图所示,已知△ABC 的面积为1平方厘米,D 、E
是AB 、AC 边的中点.求三角形OBC 的面积.
24.在如图所示的正方形中,A 、B 、C 分别是ED 、EG 、GF
的中点.请问:△CDO 的面积是△ABO 面积的几倍?
25.如图,四边形ABCD 是平行四边形,面积为72平方厘米,E 、F 分别为边AB 、
BC 的中点,请问:阴影部分的面积为多少平方厘米?
26.如图
,△ABC 中,CE=2AE ,F 是AD
的中点,△ABC 为1,那么阴影部分的面积多少?
27.如图,△ABC 中,AD 、BE 相交于点O ,△OAE 、△OAB
△OBD 的面积分别为1、2
、3,那么四边形ODCE
28.图中有半径分别为5厘米、4厘米、3厘米的三个圆,A 部分(即两小圆重叠部分)的面积与阴影部分的面积相比,哪个大?大多少?
29.如图,图中最大的长方形面积是27,最小的长方形面积是5面积.
30.阅读理解:
(1)阅读:勾股定理是几何学中一颗光彩夺目的明珠,被称为“几何学的基石”,中国是发现和研究勾股定理最古老的国家之一。
该定理是:在任何一个平面直角三角形中,两直角边的平方之和一定等于斜边的平方。
如图,在△ABC 中,B C B G C F E A D O
∠C=90°,则a ²+b ²=c ².
(2)应用:如图,在△ABC 中,∠C=90°, ①若a =3,b =4,则c = ;②若a =5,b =12,则c = ; ③若a =8,b =15,则c = ;④若a =6,c =10,则b = ; ⑤若b =12,c =15,则a = . (3)拓展: ①如图,在△ABC 中,∠A=90°,AD 是BC 边上的高. 若AD=12,AC=15,你能求出CD 、BD 、AB 的长度吗?
②根据图中信息求阴影部分的面积.
31.如图,大正方形中有三个小正方形,右上角正方形的面积是27,左下角正方形的面积是12,中间阴影正方形的2个顶点分别位于右上角和左下角正方形的中心.请问:中间阴影正方形的面积是多少?
32.图中的四边形ABCD 是平行四边形,△MAB 的面积是11
平方厘米, △MCD 的面积是5平方厘米.平行四边形ABCD 的面积是多少? 33.如图所示,平行四边形ABCD 与平行四边形AFCD 的面积都是30平方厘米.其中AF 垂直ED 于O ,AO 、OD 、AD 分别长3、4、5厘米, 求△OEF 的面积和周长.
34.如图,四边形ABCD 是直角梯形,AB=4,AD=5,DE=3, OE 垂直CD.求:(1)△OBC 的面积;(2)梯形ABCD 的面积.
35.如图,在长方形ABCD 中,AB=30厘米,BC=40厘米,P 为BC 上一点,PQ 垂直于AC ,PR 垂直于BD.求PQ 与PR 的长度之和.
a c b
B
C A A B
D C 12 15 M D C
B A
A D
O B E F C A B O
D E C A D O R Q B P C
36.图中阴影部分的面积是25平方厘米,求圆环的面积.
37.如图,正方形ABCD 的面积是64平方厘米,E 、F 分别 为所在半圆弧的中点,求阴影部分的面积.(π取3.14)
38.用棱长是1厘米的小立方体拼成如图所示的立体图形,
这个图形的表面积是多少平方厘米?
39.如图,将一个棱长为6的正方体从某个角切掉一个长、宽、
高分别为4、3、5的长方体,剩余部分的表面积是多少?
40.如图所示,有一个棱长为2厘米的正方体.从正方体的上面正中向下挖一个棱长为1厘米的正方体小洞;接着在小洞的底面正中再向下挖一个棱长为0.5厘米的小洞;第三个小洞的挖法与前面两个相同,棱长为0.25厘米
.最后得到的立体图形的表面积是多少平方厘米?
41.有一个高24厘米,底面半径为10厘米的圆柱形容器,里面装了一半水.现有一根长30厘米,底面半径为2厘米的圆柱体木棒.将木棒竖直放入容器中,使棒的底面与容器的底面接触.这时水面升高了多少厘米?
42.有一个长方体,如果长增加2厘米,则体积增加40立方厘米;如果宽增加3厘米,则体积增加90立方厘米;如果高增加4厘米,则体积增加96立方厘米.求这个长方体的表面积.
43.有大、中、小三个立方体水池,它们的内部棱长分别是6米、3米和2米.三个池子都装了半池水.现将两堆碎石分别沉没在中、小水池的水里,两个水池的水面分别升高了6厘米和4厘米.如果将这堆碎石都沉没在大水池的水里,大水池的水面会升高多少厘米?(结果精确到小数点后两位) 6 5 4 3。