小学奥数 几何计数 专题

题型：几何计数 难度：★★★★
图中可数那样规则，粗看似乎看不出其中的规律，不妨我们取出其中的一个三角形，发现它的三条边必然落在这个图形中的三条大线段上，而每三条大线段也正好能构成一个三角形，因此三角形的个数和三条大线段的取法是一一对应的关系，图中一共有10条大线段，因此有个三角形。
这个图不像我们以前数三角形那样规则粗看似乎看不出其中的规律不妨我们取出其中的一个三角形发现它的三条边必然落在这个图形中的三条大线段上而每三条大线段也正好能构成一个三角形因此三角形的个数和三条大线段的取法是一一对应的关系图中一共有10条大线段因此有个三角形
2013年6月15号六年级数学奥数题知识点《几何计数》专项练习及答案

高思奥数导引小学五年级含详解答案第10讲几何计数在小学五年级的数学学习中，几何计数作为一个重要的内容，对培养学生的观察能力和逻辑思维有着重要的作用。

本文将带领读者详解高思奥数导引小学五年级第10讲的几何计数内容。

几何计数是指通过计数方法解决与几何图形相关的问题。

它不仅要求学生掌握基本的计数技巧，还要求学生具备观察能力和逻辑思维能力，能够从几何图形中发现规律，运用数学知识解决问题。

本讲的内容主要包括三个方面：图形的计数、方格中的计数和平面图形的计数。

首先，让我们来看一下图形的计数。

在图形的计数中，学生需要利用巧妙的计数方法来确定图形中的元素个数。

常见的计数方法包括分组计数、组合计数和递推计数。

分组计数是将图形划分为若干个部分，然后计算每个部分的元素个数，最后将它们相加；组合计数是通过列举所有可能的组合情况来计算元素个数；递推计数是通过找出图形中元素数量的递推规律来计算。

接下来，我们将关注方格中的计数。

方格中的计数是指在由小方格组成的大方格中计算元素个数。

在这个过程中，学生需要了解方格的排列方式和计数规律。

常见的计数规律有根据方格的边长计算总个数、根据方格的层数计算总个数等。

通过掌握这些计数规律，学生可以更准确地计算方格中的元素个数。

最后，我们来讨论平面图形的计数。

平面图形的计数是指在平面上通过对图形的划分和分组来计算元素的个数。

在这个过程中，学生需要具备一定的观察能力和判断能力，能够将复杂的图形划分为相对简单的部分，然后计算每个部分的元素个数，并将它们相加得出最终答案。

通过学习高思奥数导引小学五年级第10讲的几何计数内容，学生不仅可以提高自己在数学领域的解题能力，还可以培养自己的观察能力和逻辑思维能力。

几何计数不但在解决实际问题中有重要的应用，而且在培养学生的空间想象力和创造力方面也有着重要的作用。

总结起来，高思奥数导引小学五年级含详解答案第10讲的几何计数涉及到图形的计数、方格中的计数和平面图形的计数。

图形计数知识要点(n m++-数线段【例1】请数出下图中线段的总条数。

【例2】数一数，下图中共有多少条线段？【例3】请问下图有多少条线段？【例4】数一数下图一共有多少条线段？【例5】数一数下图中共有多少条线段？数长方形【例6】 数一数：下图中有几个长方形（包括正方形）？【例7】 图171--中有多少个长方形（包括正方形）？【例8】 图中有多少个长方形（包括正方形）？【例9】 图中有多少个长方形（包括正方形）？【例10】 下图中有多少个长方形？FJI HGBC D E A图1-7-2图1-7-3图1-7-1【例11】下图中有多少个长方形？数正方形【例12】数一数：下图中有几个正方形？【例13】下图中共有多少个正方形？【例14】如图182--所示，平面上有16个点，每个点上都钉上钉子，形成44⨯的正方形钉阵，现在有足够的橡皮筋，请问能在这个正方形钉阵上套出多少个正方形？【例15】如图182--所示为44⨯的正方形网格由16个11⨯的小正方形构成，网格的格点都是小正方形的顶点。

那么，以网格的格点为顶点的正方形一共有个_______。

数三角形【例16】数一数下图中共有多少个三角形？【例17】数一数下图中共有多少个三角形？【例18】数一数下图一共有多少个三角形？【例19】（第十四届华罗庚少年数学邀请赛决赛试题A（小学组））如下图所示，在边长为1的小正方形组成的44方格图中，共有25个格点.在以格点为顶点的直角三角形中，两条直角边长分别是1和3的直角三角形共有________个.【例20】数一数下图一共有多少个三角形？【例21】数一数下图中的三角形个数是多少？【例22】数一数下面图形中各有多少个三角形？a 【例23】下图中共有几个三角形？图1-5-2一课一练【练习1】数一数下图一共有多少条线段？【练习2】数一数下图一共有多少条线段？【练习3】下图中有多少个长方形？【练习4】下图中，大大小小的长方形共有多少个？【练习5】下图中有多少个正方形？【练习6】下面图中有多少个正方形？【练习7】数一数下面图形中有多少个三角形？【练习8】数一数下图共有多少个三角形？补充题库【补充1】数一数，图154--中共有多少个锐角?你能用两种方法解答这个问题么？图1-5-4【补充2】下图中共有几个三角形？【补充3】数一数下图中梯形有_________个。

1.掌握计数常用方法；2.熟记一些计数公式及其推导方法；3.根据不同题目灵活运用计数方法进行计数．本讲主要介绍了计数的常用方法枚举法、标数法、树形图法、插板法、对应法等，并渗透分类计数和用容斥原理的计数思想．一、几何计数在几何图形中，有许多有趣的计数问题，如计算线段的条数，满足某种条件的三角形的个数，若干个图分平面所成的区域数等等．这类问题看起来似乎没有什么规律可循，但是通过认真分析，还是可以找到一些处理方法的．常用的方法有枚举法、加法原理和乘法原理法以及递推法等．n 条直线最多将平面分成21223(2)2n n n ++++=++……个部分；n 个圆最多分平面的部分数为n (n -1)+2；n 个三角形将平面最多分成3n (n -1)+2部分；n 个四边形将平面最多分成4n (n -1)+2部分……在其它计数问题中，也经常用到枚举法、加法原理和乘法原理法以及递推法等．解题时需要仔细审题、综合所学知识点逐步求解．排列问题不仅与参加排列的事物有关，而且与各事物所在的先后顺序有关；组合问题与各事物所在的先后顺序无关，只与这两个组合中的元素有关．二、几何计数分类数线段：如果一条线段上有n +1个点(包括两个端点)（或含有n 个“基本线段”），那么这n +1个点把这条线段一共分成的线段总数为n +(n -1)+…+2+1条数角：数角与数线段相似，线段图形中的点类似于角图形中的边． 数三角形：可用数线段的方法数如右图所示的三角形（对应法），因为DE 上有15条线段，每条线段的两端点与点A 相连，可构成一个三角形，共有15个三角形，同样一边在BC 上的三角形也有15个，所以图中共有30个三角形．ED CBA数长方形、平行四边形和正方形：一般的，对于任意长方形（平行四边形），若其横边上共有n 条线段，纵边上共有m 条线段，则图中共有长方形（平行四边形）mn 个．模块一、立体几何计数【例 1】 用同样大小的正方体小木块堆成如下图的立体图形，那么一共用了__________块小正方体。

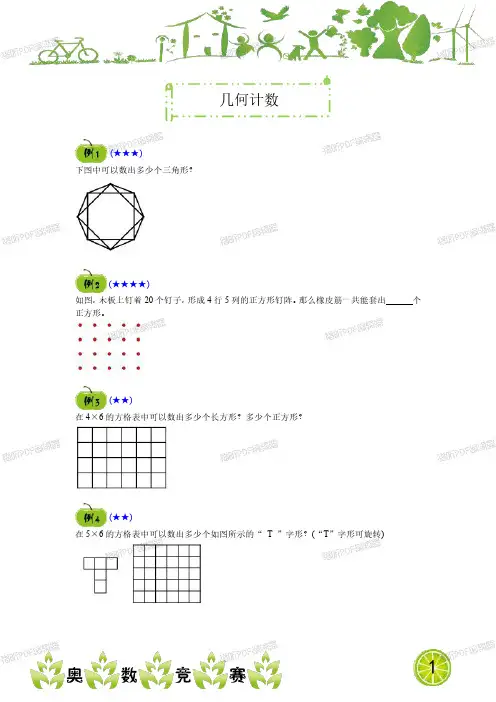
几何计数
下图中可以数出多少个三角形？
如图，木板上钉着20个钉子，形成4行5列的正方形钉阵。

那么橡皮筋一共能套出个正方形。

在4×6的方格表中可以数出多少个长方形？多少个正方形？
在5×6的方格表中可以数出多少个如图所示的“T”字形？(“T”字形可旋转) (★★★)
(★★★★)
(★★)
(★★)
下图中包含★的长方形共有多少个？
在下图中只包含一个★的长方形有多少个？
如图，用9枚钉子钉成水平和竖直间隔都为1的正方阵。

用一根橡皮筋将3枚不共线的钉子连接起来就形成一个三角形。

其中面积为1的三角形有多少个？
本讲总结
枚举法——按照大小和位置
对应法——找到对应关系
容斥原理——不重不漏
和面积相关——熟悉公式
利用图形对称性
重点例题：例4，例6，例7
(★★★)
(★★★★)
(★★★★★)。

★
1
【例5】（★★★★） 在下图中只包含一个★的长方形有多少个？
★ ★
【例6】（★★★★） 如图，用9枚钉子钉成水平和竖直间隔都为1的正方阵。用一根橡 皮筋将3枚不共线的钉子连接起来就形成一个三角形。其中面积为 1的三角形有多少个？
【例7】（★★★★★） 图中一共有多少个三角形？
本讲总结 枚举法——按照大小和位置 对应法——找到对应关系 容斥原理——不重不漏 和面积相关——熟悉公式 利用图形对称性 重点例题：例4，例5，例6
几何计数
【例1】（★★） 下图中可以数出多少个三角形？
【例2】（★★★★） 如图，木板上钉着20个钉子，形成4行5列的正方形钉阵。那么橡 皮筋一共能套出 个正方形。
【例3】（★★★） 用橡皮筋可以在6×6的格点阵中套出多少个如图所示的格点三角 形？（三角形可旋转、翻转）
【例4】（★★★） 下图中包含★的长方形共有多少个？
2

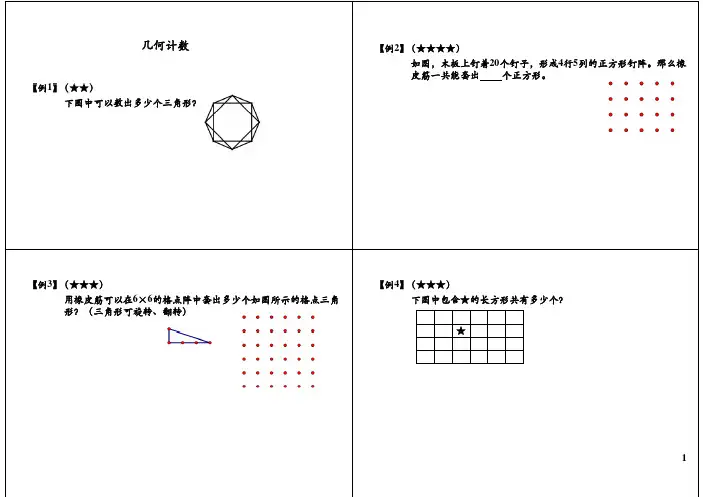
几 何 计 数 常 见 类 型
解 题 技 巧 汇 总
1．“三角形个数”常见计数题型小扫荡；
2．“长方形个数”常见计数题型大扫荡。

一、“三角形个数”常见题目
图中有______条线段？
图中有______个三角形？
图中有______个角？
三角形个数：
()121n n ＋－＋＋＋(表示基本三角形个数) -
例1
(★★★★)(2008年西城实验小升初测试题)
下图中共有______
个三角形？
-
二、“长方形个数”常见类题目
图中有______个正方形；
图中有______个长方形。

数长方形个数时，理解“长”、“宽”搭配思想。

例2
(★★)(2008年中国台湾小学数学竞赛决赛试题
)图中共有
27个三角形：16个小三角形、7个边长为2单位的三角形(包括一个倒立的)、3个边长为3单位的三角形、1个边长为4单位的三角形。

请问图中共有多少个三角形？
-
1．不重不漏；
2．“长”与“宽”有几种搭配形式？
3．“长的所有可能之和”ד宽的所有可能之和”。

例4
(★★★★)(2008年第
6届走美杯决赛第10题，10分)
由20个边长为1的小正方形拼成的一个45 长方形中有一格有“☆”。

图中含有“☆”的所有长方形（含正方形）共
______个，它们的面积总和是______。

例3
(★★★★)
在图中(单位：厘米)：
①一共有几个长方形?
②所有这些长方形面积的和是多少?。

1.掌握计数常用方法；2.熟记一些计数公式及其推导方法；3.根据不同题目灵活运用计数方法进行计数．本讲主要介绍了计数的常用方法枚举法、标数法、树形图法、插板法、对应法等，并渗透分类计数和用容斥原理的计数思想．一、几何计数在几何图形中，有许多有趣的计数问题，如计算线段的条数，满足某种条件的三角形的个数，若干个图分平面所成的区域数等等．这类问题看起来似乎没有什么规律可循，但是通过认真分析，还是可以找到一些处理方法的．常用的方法有枚举法、加法原理和乘法原理法以及递推法等．n 条直线最多将平面分成21223(2)2n n n ++++=++……个部分；n 个圆最多分平面的部分数为n (n -1)+2；n 个三角形将平面最多分成3n (n -1)+2部分；n 个四边形将平面最多分成4n (n -1)+2部分……在其它计数问题中，也经常用到枚举法、加法原理和乘法原理法以及递推法等．解题时需要仔细审题、综合所学知识点逐步求解．排列问题不仅与参加排列的事物有关，而且与各事物所在的先后顺序有关；组合问题与各事物所在的先后顺序无关，只与这两个组合中的元素有关．二、几何计数分类数线段：如果一条线段上有n +1个点(包括两个端点)（或含有n 个“基本线段”），那么这n +1个点把这条线段一共分成的线段总数为n +(n -1)+…+2+1条数角：数角与数线段相似，线段图形中的点类似于角图形中的边．数三角形：可用数线段的方法数如右图所示的三角形（对应法），因为DE 上有15条线段，每条线段的两端点与点A 相连，可构成一个三角形，共有15个三角形，同样一边在BC 上的三角形也有15个，所以图中共有30个三角形．ED CBA数长方形、平行四边形和正方形：一般的，对于任意长方形（平行四边形），若其横边上共有n 条线段，纵边上共有m 条线段，则图中共有长方形（平行四边形）mn 个．模块一、简单的几何计数【例 1】 七个同样的圆如右图放置，它有_______条对称轴．教学目标例题精讲知识要点7-8-1几何计数（一）【例 2】下面的表情图片中：，没有对称轴的个数为（）（A） 3 (B) 4 (C) 5 (D) 6【巩固】中心对称图形是：绕某一点旋转180°后能和原来的图形重合的图形，轴对称图形是：沿着一条直线对折后两部分完全重合的图形，图的4个图形中，既是中心对称图形又是的轴对称图形的有个。

1知识框架图7 计数综合 7-8 几何计数1.掌握计数常用方法；2.熟记一些计数公式及其推导方法；3.根据不同题目灵活运用计数方法进行计数．本讲主要介绍了计数的常用方法枚举法、标数法、树形图法、插板法、对应法等，并渗透分类计数和用容斥原理的计数思想．一、几何计数在几何图形中，有许多有趣的计数问题，如计算线段的条数，满足某种条件的三角形的个数，若干个图分平面所成的区域数等等．这类问题看起来似乎没有什么规律可循，但是通过认真分析，还是可以找到一些处理方法的．常用的方法有枚举法、加法原理和乘法原理法以及递推法等．n 条直线最多将平面分成21223(2)2n n n ++++=++……个部分；n 个圆最多分平面的部分数为n(n-1)+2；n 个三角形将平面最多分成3n(n-1)+2部分；n 个四边形将平面最多分成4n(n-1)+2部分……几何计数教学目标知识要点在其它计数问题中，也经常用到枚举法、加法原理和乘法原理法以及递推法等．解题时需要仔细审题、综合所学知识点逐步求解．排列问题不仅与参加排列的事物有关，而且与各事物所在的先后顺序有关；组合问题与各事物所在的先后顺序无关，只与这两个组合中的元素有关．二、几何计数分类数线段：如果一条线段上有n+1个点(包括两个端点)（或含有n个“基本线段”），那么这n+1个点把这条线段一共分成的线段总数为n+(n-1)+…+2+1条数角：数角与数线段相似，线段图形中的点类似于角图形中的边．数三角形：可用数线段的方法数如右图所示的三角形（对应法），因为DE上有15条线段，每条线段的两端点与点A相连，可构成一个三角形，共有15个三角形，同样一边在BC上的三角形也有15个，所以图中共有30个三角形．数长方形、平行四边形和正方形：一般的，对于任意长方形（平行四边形），若其横边上共有n条线段，纵边上共有m条线段，则图中共有长方形（平行四边形）mn个．例题精讲【例 1】（难度等级※※）下图的两个图形(实线)是分别用10根和16根单位长的小棍围成的．如果按此规律(每一层比上面一层多摆出两个小正方形)围成的图形共用了60多根小棍，那么围成的图形有几层，共用了多少根小棍？11【解析】 通过观察每增加一层，恰好增加6根小棍，这6根恰好是增加那一层比上一层多摆出的两个正方形多用的，即前1层用4根，前2层用4+6根，前3层用4+6×2根，前n 层用4+6×(n -1)根，现在共用了60多根，应减去4是6的倍数，所以共用小棍64根，围成的图形有11层．【例 2】 （难度等级 ※※※）用3根等长的火柴可以摆成一个等边三角形．如图用这样的等边三角形拼合成一个更大的等边三角形.如果这个大等边三角形的每边由20根火柴组成，那么一共要用多少根火柴?【解析】 把大的等边三角形分为“20”层分别计算火柴的根数：最上一层只用了3根火柴； 从上向下数第二层用了3×2=6根； 从上向下数第二层用了3×3=9根； ……从上向下数第二层用了3×20=60根；所以总共要用火柴3×（1+2+3+……+20）=630．【巩固】用三根火柴可拼成一个小“△”，若用108根火柴拼成如图所示形状的大三角形，请你数一数共有多少个三角形？【解析】 首先，需弄清形状如图的大三角形共有多少层．从上往下，第一层用331=⨯根火柴；第二层用632=⨯根火柴；第三层用933=⨯根火柴；第四层用1234=⨯根火柴；第五层用1535=⨯根火柴；…；第n 层用33n n =⨯根火柴．1根据题意，有：36912153108n ++++++=，故1234536n ++++++=，所以，8n =，即形状如图的大三角形共有8层，是边长为8根火柴的大正三角形． 然后，数出共有多少个三角形． 尖朝上的三角形共：(12345678)(1234567)(123456)+++++++++++++++++++++ (12345)(1234)(123)(12)1120++++++++++++++=(个)；尖朝下的三角形共：(1234567)(12345)(123)1050++++++++++++++++=(个)；所以，共有三角形：12050170+=(个)．本题小结：尖朝上的三角形：每一种尖朝上的三角形个数都是由1开始的连续自然数的和，其中连续自然数最多的和中最大的加数就是三角形每边被分成的基本线段的条数，依次各个连续自然数的和都比上一次少一个最大的加数，直到1为止．尖朝下的三角形的个数也是从1开始的连续自然数的和，它的第一个和恰是尖朝上的第二个和，依次各个和都比上一个和少最大的两个加数，以此类推直到零为止．【例 3】 （难度等级 ※※※）如图所示，用长短相同的火柴棍摆成3×1996的方格网，其中每个小方格的边都由一根火柴棍组成，那么一共需用多少根火柴棍?【解析】 横放需1996×4根，竖放需1997×3根共需1996×4+1997×3=13975根．【例 4】 （难度等级 ※）图中共有多少个长方形？。

7-8-1几何计数（一）教学目标1.掌握计数常用方法；2.熟记一些计数公式及其推导方法；3.根据不同题目灵活运用计数方法进行计数．本讲主要介绍了计数的常用方法枚举法、标数法、树形图法、插板法、对应法等，并渗透分类计数和用容斥原理的计数思想．知识要点一、几何计数在几何图形中，有许多有趣的计数问题，如计算线段的条数，满足某种条件的三角形的个数，若干个图分平面所成的区域数等等．这类问题看起来似乎没有什么规律可循，但是通过认真分析，还是可以找到一些处理方法的．常用的方法有枚举法、加法原理和乘法原理法以及递推法等．n 条直线最多将平面分成212232)2n n n ++++=++……个部分；n 个圆最多分平面的部分数为n (n -1)+2；n 个三角形将平面最多分成3n (n -1)+2部分；n 个四边形将平面最多分成4n (n -1)+2部分……在其它计数问题中，也经常用到枚举法、加法原理和乘法原理法以及递推法等．解题时需要仔细审题、综合所学知识点逐步求解．排列问题不仅与参加排列的事物有关，而且与各事物所在的先后顺序有关；组合问题与各事物所在的先后顺序无关，只与这两个组合中的元素有关．二、几何计数分类数线段：如果一条线段上有n +1个点(包括两个端点)（或含有n 个“基本线段”），那么这n +1个点把这条线段一共分成的线段总数为n +(n -1)+…+2+1条数角：数角与数线段相似，线段图形中的点类似于角图形中的边．数三角形：可用数线段的方法数如右图所示的三角形（对应法），因为DE 上有15条线段，每条线段的两端点与点A 相连，可构成一个三角形，共有15个三角形，同样一边在BC 上的三角形也有15个，所以图中共有30个三角形．数长方形、平行四边形和正方形：一般的，对于任意长方形（平行四边形），若其横边上共有n 条线段，纵边上共有m 条线段，则图中共有长方形（平行四边形）mn 个．例题精讲模块一、简单的几何计数【例1】七个同样的圆如右图放置，它有_______条对称轴．【例2】下面的表情图片中：，没有对称轴的个数为（）（A ）3(B )4(C )5(D )6【巩固】中心对称图形是：绕某一点旋转180°后能和原来的图形重合的图形，轴对称图形是：沿着一条直线对折后两部分完全重合的图形，图的4个图形中，既是中心对称图形又是的轴对称图形的有个。

1.掌握計數常用方法；2.熟記一些計數公式及其推導方法；3.根據不同題目靈活運用計數方法進行計數．本講主要介紹了計數的常用方法枚舉法、標數法、樹狀圖法、插板法、對應法等，並滲透分類計數和用容斥原理的計數思想．一、幾何計數 在幾何圖形中，有許多有趣的計數問題，如計算線段的條數，滿足某種條件的三角形的個數，若干個圖分平面所成的區域數等等．這類問題看起來似乎沒有什麼規律可循，但是通過認真分析，還是可以找到一些處理方法的．常用的方法有枚舉法、加法原理和乘法原理法以及遞推法等．n 條直線最多將平面分成21223(2)2n n n ++++=++……個部分；n 個圓最多分平面的部分數為n (n -1)+2；n 個三角形將平面最多分成3n (n -1)+2部分；n 個四邊形將平面最多分成4n (n -1)+2部分……在其他計數問題中，也經常用到枚舉法、加法原理和乘法原理法以及遞推法等．解題時需要仔細審題、綜合所學知識點逐步求解．排列問題不僅與參加排列的事物有關，而且與各事物所在的先後順序有關；組合問題與各事物所在的先後順序無關，只與這兩個組合中的元素有關．二、幾何計數分類數線段：如果一條線段上有n +1個點(包括兩個端點)（或含有n 個“基本線段”），那麼這n +1個點把這條線段一共分成的線段總數為n +(n -1)+…+2+1條數角：數角與數線段相似，線段圖形中的點類似於角圖形中的邊．數三角形：可用數線段的方法數如右圖所示的三角形（對應法），因為DE 上有15條線段，每條線段的兩端點與點A 相連，可構成一個三角形，共有15個三教學目標知識要點7-8-2.幾何計數（二）角形，同樣一邊在BC 上的三角形也有15個，所以圖中共有30個三角形． E DC B A數長方形、平行四邊形和正方形：一般的，對於任意長方形（平行四邊形），若其橫邊上共有n 條線段，縱邊上共有m 條線段，則圖中共有長方形（平行四邊形）mn 個．模組二、複雜的幾何計數【例 1】 如下圖在釘子板上有16個點，每相鄰的兩個點之間距離都相等，用繩子在上面圍正方形，你可以得到 個正方形．【考點】複雜的幾何計數 【難度】4星 【題型】填空【關鍵字】學而思杯，2年級，第4題【解析】 先看橫著的正方形如下圖⑴，可以得到94114++=個正方形，再看斜著的正方形如下圖⑵可以得到4個正方形，如下圖⑶可以得到2個正方形．這樣一共可以得到144220++=個正方形．⑴ ⑵ ⑶<考點> 圖形計數【答案】20個【巩固】 如圖，44⨯的方格紙上放了16枚棋子，以棋子為頂點的正方形有個．例題精講【解析】根據正方形的大小，分類數正方形．共能組成五種大小不同的正方形(如右圖)．⨯的正方形：9個；22⨯的正方形：4個；33⨯的正方形：1個；11以11⨯正方形對角線為邊長的正方形：4個；以12⨯長方形對角線為邊長的正方形：2個．故可以組成9414220++++=(個)正方形．【巩固】下圖是3×3點陣，同一行(列)相鄰兩個點的距離均為1。

第三讲几何计数
【教学重难点】
掌握常见的数图形的方法：枚举法、对应法、容斥原理、和面积相关、利用图形对称性。
【课前预习】
根据辅导书相应地给孩子预习的内容。
【教学内容】
方法一：枚举法——按照大小和位置
【例1】（★★）
下图中可以数出多少个三角形？
【例2】（★★★★）
如图，木板上钉着20个钉子，形成4行5列的正方形钉阵。那么橡皮筋一共能套出个正方形。（注意正放和斜放）
方法五：和面积相关——熟悉公式利用图形对称性
【例6】（★★★★）
如图，用9枚钉子钉成水平和竖直间隔都为1的正方阵。用一根橡皮筋将3枚不共线的钉子连接起来就形成一个三角形。其中面积为1的三角形有多少个？
【例7】（★★★★★）
图中一共有多少个三角形？
小结：
枚举法——按照大小和位置
对应法——找到对应关系
圈猪法鼠标法
4.一块木板上有13枚钉子。用橡皮筋套住其中的几枚钉子，可以构成三角形，正方形，梯形等，如图。那么一共可以构成多少个不同的正方形？
计算巩固：
1、
2、（7.88+6.77+5.66）×（9.31+10.98+10）—（7.88+6.77+5.66+10）×（9.31+10.98）
容斥原理——不重不漏
和面积相关——熟悉公式
利用图形对称性
自我挑战Hale Waihona Puke 1.下图中共有多少个正方形？
2.下图中ABCD是平行四边形，图中的线段分别与AB，AD或BE平行。图中包含阴影三角形的平行四边形共有多少个？
3.如图，18个大小相同的小正三角形拼成的四边形，其中某些相邻的小正三角形可以拼成较大的正三角形.那么图中包含“＊”的各种大小的正三角形一共有多少个？

几何计数知识框架一、公式计算法几何计数内容很广，包括数线段的条数，角的个数，长方形、正方形、三角形、平行四边形、梯形等图形的个数，也包括数立体图形的个数。

图形的计数一般有两种思考方法：公式计算法和分类计数法。

三年级学习的线段、长方形和正方形的计数就属于公式计算法。

（1）一条线段有两个端点，若这条线段上有n个点，那么线段总数是（n－1）＋（n＋2）＋…＋3＋2＋1（2）如果一个长方形的长边上有n个小格，宽边上有m个小格，那么长方形的总数是（1＋2＋3＋…＋n）×（1＋2＋…＋m）（3）如果把正方形各边都n等分，那么正方形的总数是n2＋（n－1）2＋（n－2）2＋…＋32＋22＋12上面计算线数的方法也可用于计算角的个数，而且，根据这些计数方法在以后还可以类推出立体图形的计算方法。

二、对应法将难以计数的数量与某种可计量的事物联系起来，只要能建立一一对应的关系，那么这两种事物在数量上是相同的．事实上插入法和插板法都是对应法的一种表现形式．重难点（1）分类数图形。

（2）对应法数图形。

一、 分类数图形【例 1】 下图的两个图形（实线）是分别用10根和16根单位长的小棍围成的．如果按此规律（每一层比上面一层多摆出两个小正方形）围成的图形共用了60多根小棍，那么围成的图形有几层，共用了多少根小棍？【巩固】 如图所示，用长短相同的火柴棍摆成3×1996的方格网，其中每个小方格的边都由一根火柴棍组成，那么一共需用多少根火柴棍?【例 2】 图中有______个正方形．例题精讲【巩固】 数一数：图中共有________ 个正方形。

【例 3】 右图中三角形共有 个．【巩固】 数一数图中有_______个三角形．【例 4】 图中共有多少个三角形？【巩固】 下图是由边长为1的小三角形拼成，其中边长为4的三角形有_____个。

CBA【例 5】如图，每个小正方形的面积都是l平方厘米。

则在此图中最多可以画出__________个面积是4平方厘米的格点正方形(顶点都在图中交叉点上的正方形)。

7-8-2.几何计数（二）教学目标1.掌握计数常用方法；2.熟记一些计数公式及其推导方法；3.根据不同题目灵活运用计数方法进行计数．本讲主要介绍了计数的常用方法枚举法、标数法、树形图法、插板法、对应法等，并渗透分类计数和用容斥原理的计数思想．知识要点一、几何计数在几何图形中，有许多有趣的计数问题，如计算线段的条数，满足某种条件的三角形的个数，若干个图分平面所成的区域数等等．这类问题看起来似乎没有什么规律可循，但是通过认真分析，还是可以找到一些处理方法的．常用的方法有枚举法、加法原理和乘法原理法以及递推法等．n 条直线最多将平面分成21223(2)2n n n ++++=++……个部分；n 个圆最多分平面的部分数为n (n -1)+2；n 个三角形将平面最多分成3n (n -1)+2部分；n 个四边形将平面最多分成4n (n -1)+2部分……在其它计数问题中，也经常用到枚举法、加法原理和乘法原理法以及递推法等．解题时需要仔细审题、综合所学知识点逐步求解．排列问题不仅与参加排列的事物有关，而且与各事物所在的先后顺序有关；组合问题与各事物所在的先后顺序无关，只与这两个组合中的元素有关．二、几何计数分类数线段：如果一条线段上有n +1个点(包括两个端点)（或含有n 个“基本线段”），那么这n +1个点把这条线段一共分成的线段总数为n +(n -1)+…+2+1条数角：数角与数线段相似，线段图形中的点类似于角图形中的边．数三角形：可用数线段的方法数如右图所示的三角形（对应法），因为DE 上有15条线段，每条线段的两端点与点A 相连，可构成一个三角形，共有15个三角形，同样一边在BC 上的三角形也有15个，所以图中共有30个三角形．E DCB A数长方形、平行四边形和正方形：一般的，对于任意长方形（平行四边形），若其横边上共有n 条线段，纵边上共有m 条线段，则图中共有长方形（平行四边形）mn个．例题精讲模块二、复杂的几何计数【例1】如下图在钉子板上有16个点，每相邻的两个点之间距离都相等，用绳子在上面围正方形，你可以得到个正方形．【考点】复杂的几何计数【难度】4星【题型】填空【关键词】学而思杯，2年级，第4题【解析】先看横着的正方形如下图⑴，可以得到94114++=个正方形，再看斜着的正方形如下图⑵可以得到4个正方形，如下图⑶可以得到2个正方形．这样一共可以得到144220++=个正方形．⑴⑵⑶<考点>图形计数【答案】20个【巩固】如图，44⨯的方格纸上放了16枚棋子，以棋子为顶点的正方形有个．【解析】根据正方形的大小，分类数正方形．共能组成五种大小不同的正方形(如右图)．11⨯的正方形：1个；⨯的正方形：4个；33⨯的正方形：9个；22以11⨯长方形对角线为边长的正方形：2个．⨯正方形对角线为边长的正方形：4个；以12故可以组成9414220++++=(个)正方形．【巩固】下图是3×3点阵，同一行(列)相邻两个点的距离均为1。

小学奥数几何计数一、知识点（1）分类：数图形、数角、数长方形、数正方形、数三角形、数综合图形等。

（2）方法：①基本图形法（一个基本图形、二个基本图形、三个基本图形。

）②标号计数法③公式法注：基本图形法与标号计数法均为列举法。

（3）特殊：长方形个数=长边总线段数×宽边总线段数正方形个数=a×b+（a-1）×（b-1）+（a-2）×（a-2）+….注：总线段数、a与b表示的是基本图形数二、基础题1、数出右图中总共有多少个角2、下列图形各有几条线段3、数一数图中长方形的个数4、数一数共有多少条线段？共有多少个三角形？5、数一数图中有多少个正方形（其中每个小方格都是边长为1个长度单位的正方形）6、数一数图中三角形的个数三、巩固题1、共有多少个三角形？2、数一数图中三角形的个数3、下图共有几个正方形?4、右图的图形中一共有多少个三角形?5、一条直线上共有50个点,可以数出( )条线段.6、下图共有几个三角形?.四、提高题1、下图一共有( )个正方形？2、下图中一共有多少个三角形?3、有一批长度分别为1,2,3,4,5,6,7,8,9,10和11厘米的细木条,它们的数量都足够多,从中适当选取3根木条作为三条边.可围成一个三角形,如果规定底边是11厘米长,你能围成多少个不同的三角形?4、数一数图中一共有多少个三角形？5、下图共有( )个三角形.6、下图共有多少个长方形?五、竞赛题1、数一数图中一共有多少个三角形？2、算一算图中所有正方形的面积之和（其中每个小方格都是边长为厘米的正方形）.3、数一数图中有多少个长方形？六、练习题1、如右图中，各个图形内各有多少个三角形？2、如下图中，共有多少个角？（小于平角）3、如右图数一数图中长方形的个数.4、下图中共有( )条角。

5、数一数图中有多少个长方形？6、下图一共有( )个正方形？。

1.掌握计数常用方法；2.熟记一些计数公式及其推导方法；3.根据不同题目灵活运用计数方法进行计数．本讲主要介绍了计数的常用方法枚举法、标数法、树形图法、插板法、对应法等，并渗透分类计数和用容斥原理的计数思想．一、几何计数在几何图形中，有许多有趣的计数问题，如计算线段的条数，满足某种条件的三角形的个数，若干个图分平面所成的区域数等等．这类问题看起来似乎没有什么规律可循，但是通过认真分析，还是可以找到一些处理方法的．常用的方法有枚举法、加法原理和乘法原理法以及递推法等．n 条直线最多将平面分成 21223(2)2n n n ++++=++……个部分；n 个圆最多分平面的部分数为n (n -1)+2；n 个三角形将平面最多分成3n (n -1)+2部分；n 个四边形将平面最多分成4n (n -1)+2部分……在其它计数问题中，也经常用到枚举法、加法原理和乘法原理法以及递推法等．解题时需要仔细审题、综合所学知识点逐步求解．排列问题不仅与参加排列的事物有关，而且与各事物所在的先后顺序有关；组合问题与各事物所在的先后顺序无关，只与这两个组合中的元素有关．二、几何计数分类数线段：如果一条线段上有n +1个点(包括两个端点)（或含有n 个“基本线段”），那么这n +1个点把这条线段一共分成的线段总数为n +(n -1)+…+2+1条数角：数角与数线段相似，线段图形中的点类似于角图形中的边．数三角形：可用数线段的方法数如右图所示的三角形（对应法），因为DE 上有15条线段，每条线段的两端点与点A 相连，可构成一个三角形，共有15个三角形，同样一边在BC 上的三角形也有15个，所以图中共有30个三角形．教学目标知识要点7-8-2.几何计数（二）ED CBA数长方形、平行四边形和正方形：一般的，对于任意长方形（平行四边形），若其横边上共有n 条线段，纵边上共有m 条线段，则图中共有长方形（平行四边形）mn 个．模块二、复杂的几何计数【例 1】 如下图在钉子板上有16个点，每相邻的两个点之间距离都相等，用绳子在上面围正方形，你可以得到 个正方形．【考点】复杂的几何计数 【难度】4星 【题型】填空 【关键词】学而思杯，2年级，第4题【解析】 先看横着的正方形如下图⑴，可以得到94114++=个正方形，再看斜着的正方形如下图⑵可以得到4个正方形，如下图⑶可以得到2个正方形．这样一共可以得到144220++=个正方形．⑴ ⑵ ⑶<考点> 图形计数 【答案】20个【巩固】 如图，44⨯的方格纸上放了16枚棋子，以棋子为顶点的正方形有 个．【解析】 根据正方形的大小，分类数正方形．共能组成五种大小不同的正方形(如右图)．11⨯的正方形：9个；22⨯的正方形：4个；33⨯的正方形：1个；以11⨯正方形对角线为边长的正方形：4个；以12⨯长方形对角线为边长的正方形：2个． 故可以组成9414220++++=(个)正方形．例题精讲【巩固】下图是3×3点阵，同一行(列)相邻两个点的距离均为1。