基数和序数含义

英语数词用法详解数词部分▲掌握分数、时间、日期的表达法;复习要点一基数词基数词用来表示数目,或者说表示数量的词叫基数词;最基本的基数词如下1 one11 eleven100 a hundred2 two12 twelve20 twenty1000 a thousand3 three13 thirteen30 thirty1,000,000 a million4 four14 fourteen40 forty10,000,000 ten million5 five15 fifteen50 fifty100,000,000 a hundred million6 six16 sixteen60 sixty1,000,000,000 a billion7 seven17 seventeen70 seventy8 eight18 eighteen80 eighty9 nine19 nineteen90 ninety10 ten说明：1．13—19是由个位数加后缀-teen构成;注意其中13、15的拼写是thirteen和fifteen;2．20—90由个位数加后缀-ty构成,注意其中20—50的拼写分别是twenty, thirty, forty 和fifty;80的拼写是eighty;3．其它非整十的两位数21—99是由整十位数加连字符“-”,再加个位数构成;如： 81 eighty-one;4．101—999的基数词先写百位数,后加and再写十位数和个位数;如： 691 six hundred and ninety-one;5．1000以上的基数词先写千位数,后写百位数,再加and,最后写十位数和个位数;如：5893 five thousand eight hundred and ninety-three;在基数词中只有表示“百”、“千”的单位词,没有单独表示“万”、“亿”的单位词,而是用thousand千和million百万来表达,其换算关系为：1万=10 thousand;1亿=100 million; 10亿=a thousand million=a billion;6．多位数的读法：11000以上的多位数,要使用计数间隔或逗号“,”;即从个位起,每隔三位加一个间隔或逗号;第一个间隔或逗号前是thousand千,第二个间隔或逗号前是million百万,第三个间隔或逗号前是a thousand million或a billion十亿;2每隔三位分段以后就都成了101—999;读的时候十位数或个位数的前面一般要加and;如：888,000,000读作：eight hundred and eighty-eight million;基数词的用法：1. 基数词在句中的作用基数词的作用相当于名词和形容词,在句中可作定语、主语、宾语介宾、表语、同位语等;例如：Three and five is eight. 3+5=8 作表语How many oranges do you want 你要多少桔子I want eight. 我要八个;作宾语There are eight boats in the lake. 湖里有八条小船;作定语2．Hundred, thousand, million, dozen, score这些词前面如有表示具体数字的词,它们不能加“s”,反之则须加“s”,并要与of短语连用;例如：three hundred people, five thousand years；thousands of people, hundreds of students, thousands of trees二序数词表示顺序的词,叫序数词;序数词用来表示数词顺序;除特殊情况外,序数词一般都由相应的基数词加后缀-th构成;说明：1．英语中表示第一、第二、第三的序数词属特殊形式,要注意它们的拼写;2．表示“几十”的序数词通常是将基数词词尾y变成i再加上后缀-eth;3．其余的二位数序数词是以相应的整十基数词加个位序数词;如：fifty-first 第五十一;4．少数序数词拼法不规则,如：fifth第五,eighth第八,ninth第九,twelfth第十二等;注意：1．序数词可缩写为阿拉伯数字加序数词最后两个字母;例如：第一：the first=1st 第二：the second=2nd第三：the third=3rd 第五：the fifth=5th第九十七：the ninety-seventh=97th第一百零一：the one hundred andfirst=101st2．编了号的事物要用基数词表示顺序,但是基数词要后置;例如：第一课：Lesson One 第三十二页：Page 32第305房间：Room 305 第12路公共汽车：Bas No.12序数词的用法序数词表顺序,主要作定语,其前面须加上定冠词the,此外,也作主语、宾语、表语和定语等,这时,被它所修饰的名词往往被省略;如：The first person to arrive is Kate.例如：The first is bigger than the second. 作主语第一个比第二个大;Give me the first. 作宾语把第一个给我;She’s often the first to go to school. 作表语她经常第一个去上学;We’re going to learn the eighth lesson. 作定语我们将要学习第八课;三分数表达法先写基数词表示分子,后写序数词表示分母,如果分子大于1时,分母用复数;如：one-fourth, two-fifths, three-tenths四小数表达法小数点前的整数按基数词的规则表示,小数点写作point, 小数后的数字应按其数字直接表示出来;如：18.38可写成：eighteen point three eight;注意：小数在句中常作定语,尤其在比较方式状语从句中被使用;如：This stone is 3.5 times heavier than that one.五百分数表达法根据学生情况选择使用在数词后加percent;例如：15%读作：fifteen percent；60%读作：sixty percent六表示语数根据学生情况选择使用1…几倍大小长短,数量=…几倍或分数+the sizelength, amount;例如：The earth is forty-nine times the size of the moon.地球是月球的49倍;2…比…几倍=…倍数或分数+形容词副词比较级+than+被比部分;例如：His house is three times bigger than mine. 他的房子比我的房子大三倍;3…是…倍=…倍数或分数+as +形容词+as +被比部分;例如： This factory is four times as big as that one. 这个工厂是那个工厂的四倍;七表示约数根据学生情况选择使用1“多于”用more than或over;例如：The street is overmore than 500 metres long. 这条街有500多米长;2“小于”用less than;例如：Three are less than 30 people in the classroom. 教室里不到三十人;3“或…以上”用or more;例如：The building can hold 5000 people or more.那座建筑物可容纳5000人或5000人以上;4“或…以下”用or less;例如：We can finish the work in two weeks or less.我们可以在两周内或不到两周完成这件工作;5“大约”用about, around, nearly等;例如：The box weighs about 50 pounds. 这箱子重约50镑;6“左右”用or so.如：In the past ten years or so, they have changed a lot. 在过去的十年里,他们改变了许多;八年、月、日和时间的表达法1．年份用基数词表达,分两位一读,年份前用介词in;例如：1999 nineteen ninety-nine2000 two thousand2001 two thousand and one2．月份的第一个字母要大写,有些月份名称有缩写形式;例如：一月JanuaryJan., 二月FebruaryFeb., 三月MarchMar., 四月Apr.,五月May, 六月June, 七月July, 八月AugustAug.,九月SeptemberSep., 十月OctoberOct., 十一月NovemberNov., 十二月DecemberDec.;3．日期的表达要用序数词,读时前面要加定冠词the,介词要使用on;例如：在6月1日：on June 1st 读作：on June the first.年、月、日同时表达时,一般应先写月、日、后写年;如：在2001年5月4日：on May 4 th, 2001;4．年代用基数词的复数表示;例如：20世纪90年代：nineteen nineties；21世纪20年代：twenty twenties 5．时间表达法：时间可用顺读法或倒读法两种方式表达;例如：5：00 five o’clock6：18 six eighteen或 eighteen past six12：15 twelve fifteen 或fifteen a quarter past twelve4：30 four thirty或 half past four6：45 six forty-five a quarter to seven注意：1表示整点时间,直接用基数词表达,后边可接o’clock 也可不加;表达“几点几分”时,绝不能用o’clock;2表达“15分”或“45分”时,常用quarter刻;3在倒读法中,如果钟点不过半,须用“分钟数+past+钟点数”的形式；如果钟点过半,则用“差多少分钟数+to+全钟点下个钟点数”的形式;两组与数词有关的介词短语：⑴ in+定冠词the+数词的复数形式,表示年代;如：in the 1870s或1870’s⑵ in+物主代词+数词的复数形式,表示某人的年龄;如：in one’s thirties;有时在物主代词后面可加上形容词early或late使其含义更确切些;如：The young man is at most in his early thirties.注意：带有数词的名词作定语的表达：a seven-year-old boy,a hundred-metre race英语分数、倍数、小数和百分数的表示方法一、分数的表示法分数由基数词和序数构成——分子用基数词,分母用序数,分子超过“1”时,分母用复数：a one sixth1/6, two thirds2/3, three fifths3/5说明1 1/2 通常读作 a one half,一般不读作a second;2. 1/4 可读作a one fourth,也可读作a one quarter;3. 分子超过“1”分母之所以用复数可以这样理解：“三分之二”即两个two三分之一third,既然是两个“三分之一”,那“三分之一”当然要用复数,即用thirds;4. 在数学上,为了简洁起见,分子和分母均可用基数词,其间用介词over：3/4 读作three over four对于比较复杂的分数通常采用此读法5. 带分数的读法：在整数与分数之间用and连接：five and two thirds二、倍数的表示法表示倍数时通常借助half, double, twice, three times等之类的词：Half of the apples are bad. 一半苹果是坏的;His homework is not yet half done. 他的作业还没完成一半;He eats twice what I eat. 他的食量是我的两倍;比较以下三句,虽然表达形式不同,但含义相同：1. This rope is three times as long as that one. 这根绳子是那根的三倍长;2. This rope is three times longer than that one. 这根绳子是那根的三倍长;3. This rope is three times the length of that one. 这根绳子是那根的三倍长;第1句和第3句的意思比较清楚,但第2句常容易误解,有人认为它与其他两句意思不同,应理解为“这根绳子比那根绳子长三倍”,但绝大多数语法学家并不这样认为,而是认为以上三句意思相同;三、小数的表示法与汉语一样,小数点前的数按普通基数词的读法读,小数点后的数按单个数字一一读出;小数点后的0通常读作oh,有时也读作nought或zero,小数点读作point：one point five six1.56, ten point three oh five说明被大于“1”的小数修饰的名词要用复数,如说 1.3 meters,不说1.3 meter；即使是被小于“1”的小数修饰,名词也通常可以用复数：One centimeter equals0.3937 inches. 1厘米等于0.3937英寸;四、百分数的表示法百分数由基数词或小数和百分号%组成,百分号%读作per cent：fifteen percent15%, ero point six percent0.6%说明百分数后接名词时有时用介词of,有时不用：30% of the students30%的学生,a 30% chance30%的把握;两者的区别是：后接介词of时,percent 为名词,of表示整体中的部分；不接介词of时,percent 为形容词此时不表示整体与部分的关系,再比较：6 percent of the interest＝利息中的百分之六,at 6 percent interest＝按百分之六的利息;英语序数词用法指导一、序数词的表示法1. 以下是最基本的序数词,学习者必须牢记：first第1, second第2, third第3, fourth 第4, fifth第5, sixth第6, seventh第7, eighth第8, ninth第9, tenth 第10, eleventh第11, twelfth第12, thirteenth第13, fourteenth第14, fifteenth第15, sixteenth第16, seventeenth第17, eighteenth第18, nineteenth第19, twentieth第20, thirtieth第30, fortieth第40, fiftieth第50, sixtieth第60, seventieth第70, eightieth第80, ninetieth第90;说明①许多序数词是由相应的基数词后加th构成的,如：four / fourth,six / sixth,ten / tenth,sixteen / sixteenth,但是nine变为序数词是ninth,而不是nineth;②twentieth, thirtieth, fortieth 等表示整十的序数词,由相应的基数词将词尾y改为ie,再加th 构成;③first, second, third 通常可缩写为1st, 2nd, 3rd;凡是以th结尾的序数词可缩写为“基数词+th”：4th, 5th, 9th, 11th, 60th, 128th等;2. 非整十的多位数,将个位数变成序数词即可：twenty-first第21,thirty-sixth 第36,ninety-ninth第99,three hundred and sixty-fifth第365等;3. hundred, thousand, million 等序数词形式为hundredth, thousandth, millionth 等：five hundredth 500th 第500 ten thousandth 10, 000th 第10000 注意：这类词前用数字“一”时,这个“一”只用one,不用a：one hundredth 第100不说a hundredth二、既可序数词也可用基数词的场合1. 日期的表示法通常用序数词,也可用基数词,如“5月5日”在书面语中通常写成5 May英或May 5th美,而在口语中则通常说成the fifth of May,May the fifth英, May fifth美等;2. 在类似编号的场合,用序数词应放在被修饰词语之前,若用基数词则置于其后：the First Lesson / lesson one 第一课the tenth chapter / chapter ten 第10章the sixth line / line 6 第6 行the third part / part three 第三部分但是,在许多情况下,用基数词比用序数词更合适、更方便：Book One 第一册Room 805 805房page 110 第110页Bus Number Ten 第10路公共汽车三、序数词前使用冠词应注意的两点1. 序数词前通常要用定冠词It’s the third time I’ve been here. 这是我第三次来这儿;The second is better than the first. 第二个比第一个好;说明①表示考试或比赛等的名次时,通常省略定冠词：She was the third in the exam. 她考试得了第三名;②序数词用作副词时也通常不用冠词：He came first. 他先来;I’ll have to finish my homework first. 我得先把作业做完;③有些习语中的序数词前没有冠词：at first 开始at first sight 乍看起来first of all 首先④但若序数词前用了物主代词或名词所有格,则不能再用定冠词：his second wife 他的第二个妻子Tom’s third book 汤姆的第三本书2. 序数词前有时可用不定冠词,表示次第在原有基础上的增加：A second student stood up. 又一个第二个学生站了起来;I want to read the book a third time. 这本书我想读第三次;序数词前用定冠词和不定冠词的区别在于,定冠词表特指,不定冠词表泛指,有类似another的意思,但比another 的意思更明确：I like the third girl. 我喜欢第三个女孩;至少有三个女孩供选择,特指I saw a third girl. 我又看见了第三个女孩;暗示原来已看见两个,这已是第三个英语基数词的用法一、基数词的表示法1. 以下是最基本的基数词,学习者必须牢记：one1, two2, three3, four4, five5, six6, seven7, eight8, nine9, ten10, eleven11, twelve12, thirteen13, fourteen14, fifteen15, sixteen16, seventeen17, eighteen18, nineteen19, twenty20, thirty30, forty40, fifty50, sixty60, seventy70, eighty80, ninety90,a hundred100, a thousand1000, a million1000000, a billion 十亿2. 21—99 的表示法;先说“几十”,再说“几”,中间加连字号：twenty-one21, thirty-six36, forty-five45, ninety-nine99等;3. 101—999的表示法;先说“几百”,后接and,再加末尾两位数或末位数：one hundred and one101, five hundred and thirty530, seventy hundred and eighty-nine7894. 1000 以上的基数词的表示法;先从右至左数,每三位数加一个逗号即以此把数目分为若干段;第一个逗号前的数为thousand千,第二个逗号前的数million百万,第三个逗号前的数为billion十亿,第四个逗号前的数为trillion万亿,然后一段一段地数：9, 883 nine thousand, eight hundred and eighty-three65, 359 sixty-five thousand, three hundred and fifty-nine265, 468 two hundred and sixty-five thousand, four hundred andsixty-eight60, 263, 150 sixty million, two hundred and sixty-three thousand, one hundred and fifty说明①英语没有“万”这个单位,要表示“万”须借用thousand,如“一万”用“十千”表示ten thousand,“十万”用“百千”表示one hundred thousand;②hundred, thousand, million, billion 等词在读数时不带复数词尾-s即用单数形式;③在hundred 后通常加上连词,不过此and 在美国英语中可以省略;若读数中没有hundred,则在thousand后加and;④一个数的最高位若为“一”,这个“一”可用a或one表示,但在数字中间的“一”,则只能用one,不能用a：1600 a one thousand and six hundred6100 six thousand and one hundred 其中的one 不可改为a⑤在非正式场合,人们也常以hundred 为单位来读数,对于1100至1900之间的整数尤其如此参见年代的读法：It cost fifteen hundred pounds. 这东西花了1500英镑;二、时刻、日期、年份等的表示法1. 时刻的表示法①若为整点钟,则直接读相应的基数词；若为非整点钟,则分别以“时”和“分”为单位用相应的基数词读出：twelve12, eight twenty8:20, nine forty-five9:45 ②对于带“分”的时间,也可借助past过和to差这两个介词来表示在美国英语中用after表示“过”;但是注意,这样表示时“分”不能超过30,否则应作处理,如9.38应处理成“10点差22分”：18 eighteen minutes past after nine = nine eighteen46 fourteen minutes to eleven = ten forty-six以上分钟后带了minutes一词;若“分”为5, 10, 15, 20 等五的倍数,则可省略minutes：05 five minutes past after eight = eight five20 twenty minutes past after nine =nine twenty若“分”为15或45,可借用quarter 一词；若“分”为30,可借用half一词：15 a quarter past six 8.45 a quarter to nine 10.30 half past ten说明时刻表示法分为12小时编时制和24小时编时制;2. 日期的表示法：日期的写法书面语和读法口语稍有不同,如“十月一日”可以写成October 1, October 1st, 1 October, 1st October, the 1st of October 等,表示月份的词也可用缩略式,如Oct. 1, 1 Oct. 1,但是在口语中通常只有两种读法October the first或the first of October;说明日期与星期排列时,通常是星期在前,日期在后：He arrived on Friday, May 10. 他于5月10日星期五到达;3. 年份的表示法：通常以“百”为单位来读;如1986年通常读作nineteen hundred and eighty-six,除非在正式场合,其中的hundred and通常都省,但在通常情况下不能按普通基数词的读法那样读成one thousand nine hundred and eighty-six;不过,像1500这样的年份可以有两种读法one thousand five hundred和fifteen hundred,而2000年通常读作two thousand,2003年读作two thousand and three;若表示某个年代,则按类似以下的读法：1980s 读作nineteen-eighties20世纪80年代, 1600s 读作sixteen hundreds17世纪头10年,即1600—1610,比较：1300 thirteen hundred1300年;三、用于复数形式的基数词1. 表示整十的基数词用复数形式可以表示人的岁数或年代：in the sixties 在60年代in one’s thirties 在某人30多岁时2. 基数词转化为名词,可用复数形式：How many twos are there in ten 10里面有几个2The soldiers marched in tens. 士兵们10人一排前进;3. 某些习语中也用复数形式的基数词：in by twos and threes 三三两两地at sixes and sevens 乱其八糟。

什么是基数和序数有什么区别基数和序数是数学中常用的两个概念，它们在数学运算和语言表达中有着不同的应用和含义。

本文将详细介绍基数和序数的定义、区别和应用。

一、基数的定义和应用基数是用来计量事物数量或进行计数的数值，也称为计数数目。

基数通常用于表示具体的数量，例如表示集合中元素个数、某一事件发生的次数等。

基数可以是自然数、整数或实数，并且基数具有常用的算术运算规则，如加减乘除等。

在数学中，经常使用基数来表示集合的大小、统计数据的数量等。

例如，有4只苹果、10辆小汽车等。

二、序数的定义和应用序数是用来表示事物在某个顺序或次序中的位置的数值，也称为次序数。

序数通常用于表示事物的排列顺序和等级，以及进行比较和排序。

序数是基于基数的概念而建立的，它具有相对性和顺序性。

序数与基数不同的是，序数除了表示数量，还表示顺序；而基数只表示数量。

例如，第一个、第二个、第三个等。

序数有其特定的写法规则，一般以英文字母或词汇的形式表示，如"first"、"second"、"third"等。

序数也可以通过添加后缀"-th"（或"-st"、"-nd"、"-rd"）来构成，如"10th"、"21st"、"32nd"等。

三、基数和序数的区别基数和序数之间存在明显的区别和差异：1. 含义不同：基数表示具体数量，而序数表示次序或顺序。

2. 表示方式不同：基数以数字形式表示，而序数以词汇或字母形式表示。

3. 在使用语境上有所差异：基数用于计数和量化，序数用于排序和比较。

4. 应用范围不同：基数可以适用于各个领域和场景，而序数主要用于表达顺序和等级。

四、基数和序数的应用举例1. 基数的应用举例：- 有7个篮球运动员参加比赛。

- 甲班有30名学生。

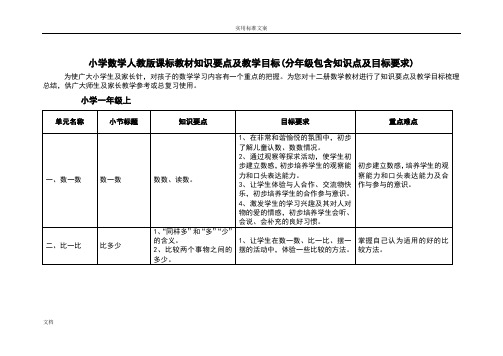
小学数学人教版课标教材知识要点及教学目标(分年级包含知识点及目标要求)为使广大小学生及家长针，对孩子的数学学习内容有一个重点的把握。

为您对十二册数学教材进行了知识要点及教学目标梳理总结，供广大师生及家长教学参考或总复习使用。

小学一年级上文档文档文档文档文档文档文档文档文档文档小学一年级下单元名称小节标题知识要点目标要求重点难点一、位置上下确定物体上下的位置和顺序1、在具体的活动中，让学生体验上下的位置关系，初步培养学生的空间观念。

确定物体上下的位置和顺序，并能用自己的语言表达2、初步培养学生按一定的顺序进行观察的习惯3、初步培养学生的想象能力和解决问题的策略意识，使学生在活动中获得积极的情感体验。

重点：能确定物体上下的位置和顺序，并能用自己的语文试表述难点：让学生体验上下位置的相对性。

前后确定物体前后的位置与顺序1、学生能在具体的生活实践或游戏情境中，体验前与后的位置与顺序。

2、能准确地确定物体前后的位置与顺序。

3、培养学生关于前后的空间观念。

4、培养学生的爱国主义精神。

重点：前与后的位置与顺序难点：学生前后空间观念的培养。

左右认识“左右”的位置关系1、在生活中看关于“左右”的真实情境激发学生的学习兴趣。

2、能初步运用“左右”的数学知识解决实际问题。

3、认识“左右”的位置关系，体会其相对性。

重点：认识“左右”的位置关系，正确确定“左右”。

难点：“左右”的相对性。

文档位置在具体情境中，根据行列确定物体的位置教学要求：1、能够在具体情境中，根据行列确定物体的位置。

2、培养观察、分析、比较的思维能力。

3、培养团结、合作、互助的精神。

重点：根据行列确定某一物体的位置。

难点：能用语言去描述某一物体的位置。

二、20以内的退位减法十几减九正确进行十几减9的计算1、通过对问题情境的探索，使学生在已有经验基础上自己得出计算十几减9的各种方法；通过比较，使学生体验比较简便的计算方法。

2、使学生理解十几减9的退位减法的思维过程，并能正确进行十几减9的计算。

RJ版一年级：第一单元。

本单元知识盘点：1.数数。

数出10以内物体的数量，根据物体的个数，用1~10这十个数来表示。

2.数数的方法。

数一种物体的数量时，从1开始，按照一定的顺序点数，数到最后一个物体所对应的那个数，就是这种物体的总个数；多种物体混放时，边数边做标记不容易出错。

3.比多少的意义。

有两种物体，当把两种物体一一对应后，都没有剩余时，这两种物体的数量同样多；其中一种物体有剩余时，有剩余的那种物体就多，没有剩余的那种物体就少。

4.比多少的方法。

一一对应的方法。

本单元知识点易错汇总：1.数数要有方法，用手或笔尖点着物体，一个一个地数，数到几，就用数（shù）几来表示。

2.多种物体放在一起时，要按一定的顺序边数边做标记，避免重数或漏(lòu)数。

3.比较物体的多少时，要采用一一对应的方法，不能只看物体的首尾是否对齐。

本单元重难点内容：1. 掌握数数的方法，能正确数出物体的个数（重点）。

2. 能有序地进行数数（难点）。

3. 理解“同样多”“多”“少”的含义（重点）。

4. 会用一一对应的方法比较物体的多少（难点）。

本单元知识重要考点：1.数数。

2.比多少。

第二单元。

本单元知识盘点：1.确定上、下的标准。

位置在高处的就是“上”，与“下”相对；位置在低处的就是“下”，与“上”相对。

2.判断上、下位置关系的方法。

首先确定参照物，再确定所描述的物体是在参照物的上面，还是在参照物的下面。

3.确定前、后的标准。

一般面向的方向是“前”，背对的方向是“后”，“前”和“后”是相对的。

4.判断前、后位置关系的方法。

以参照物为标准，参照物面向的方向是前，背对的方向是后。

5.确定左、右的标淮。

以自己的左、右手为标准，与左手对应的一边是左边，与右手对应的一边是右边。

本单元知识点易错汇总：1.上、下位置关系是相对而言的，两者相互依存，不能孤立存在。

描述物体的上、下位置关系时，一定要说“谁在谁的上（或下）面”或者“谁的上（或下）面是谁”。

《初等代数研究》自然数的基数理论和序数理论姓名：***班级：数信2011级1班学号：************日期：2013年12月20日自然数的基数理论和序数理论摘要：自然数是人类最早认识的数，随着人类社会的发展，数也随之被扩充，从自然数到分数，再到负数……数系的每一次扩充都是人类文明史的一次飞跃，本文论述的是人类最早认识的自然数两种理论，基数理论和序数理论的定义及基本运算，用有限集的基数给出自然数的及其顺序和运算的定义，用公理法研究自然数集。

关键词：自然数；基数理论；序数理论一、自然数1.1 自然数的产生在人类社会发展初期，人们还不会用数来表示物体的多少，而是采取一一对应的方法进行比较的。

例如，牧羊人在统计羊的数目时常常用石子代表羊，一颗石子对应着一只羊，早晨放牧时这样检查羊的只数，晚上放牧归来用同样的方式检查羊是否丢失。

又如：狩猎时常把武器和狩猎者一一搭配起来，也即一人一件。

经过长期的实践，才逐步形成“多”和“少”的概念。

随着社会生产力的发展和物质交换的增多，人类在长时间反复应用集合来表示多少的过程中，渐渐的把数从具体的集合中抽象出来，逐渐的创造了抽象的数字符号，这就是最早的自然数。

不同地域，不同文明的数字符号并不相同，其功能却相同。

1.2 自然数的组成：自然数起源于数数，在数物体的时候，用来表示物体个数的1 , 2 , 3 , 4，……叫做自然数。

1994年11月国家技术监督局发布的《中华人民共和国国家标准，物理科学和技术使用的数学符号》中，将自然数集记为自然数的基本单位是“1”，任何非0的自然数都由若干个“1”组成。

一个物体也没有用符号“0”表示，0也是自然数。

“0”的含义众多，表示没有，仅仅是最初的含义。

随着人类研究的不断深入，对“0”的人是也不断的发展。

“0”不仅表示没有，还可以表示一些特定的数值。

例如：“这里的海拔为0米”，并不是说这里没有高度，而是表示这里相对于海平面的高度为0米；在测量工具上，“0”刻度线是计量的起点；在温度计上，“0”表示一个标准大气压下，冰水混合物的温度数值；在运算时，“0”还有占位的作用等。

《6~9 的认识分与合》学历案一、学习主题6~9 的认识及分与合二、学习目标1、学生能够正确地数出 6、7、8、9 这四个数字，并且能够认读和书写。

2、理解 6~9 的基数和序数含义，能够区分几个和第几个。

3、掌握 6~9 的分与合，能够通过操作和观察，有序地写出 6~9 的分与合的式子。

三、学习重难点1、重点（1）正确数出 6~9 各数，掌握其顺序和大小。

（2）理解 6~9 的分与合。

2、难点（1）基数和序数的区别。

（2）有序地写出 6~9 的分与合。

四、学习资源1、数字卡片 6~9。

2、小棒若干。

3、计数器。

五、学习过程（一）导入通过展示一些数量在 6~9 之间的物体图片，如 6 个苹果、7 朵花、8 只鸭子、9 个气球，引导学生观察并数一数，从而引出 6~9 这几个数字。

（二）认识 6~91、数出 6~9（1）出示主题图，让学生观察并说说图中都有什么，分别有几个。

（2）请学生用小棒分别摆出 6、7、8、9，一边摆一边数。

2、数字 6~9 的写法（1）教师在黑板上示范 6~9 的写法，强调笔顺和占格。

（2）学生在练习本上模仿书写。

3、 6~9 的基数和序数含义（1）通过排队游戏，让学生理解几个和第几个的区别。

例如，让 9 个学生排成一队，从前往后数，第 6 个同学是谁。

（2）结合生活实例，让学生说一说“6 个”和“第 6 个”的不同。

（三）6~9 的分与合1、 6 的分与合（1）让学生用 6 根小棒分一分，看看有几种分法。

（2）学生操作后，展示并交流分法，得出 6 可以分成 1 和 5、2 和4、3 和 3、4 和 2、5 和 1 。

（3）引导学生有序地记忆 6 的分与合。

2、 7 的分与合（1）用同样的方法，让学生用7 根小棒分一分，得出7 的分与合。

（2）同桌之间互相说一说 7 的分与合。

3、 8 的分与合（1）让学生自己动手用 8 个圆片分一分，记录分的结果。

（2）小组内交流，互相补充完整 8 的分与合。

第四章学前儿童数的认知发展与教育本章主要内容第一节计数与基数认知能力的发展与教育第二节序数的认知发展与教育第三节数的分解组成能力发展与教育第四节加减运算能力的发展与教育第一节计数与基数认知能力的发展与教育一、计数与基数的含义计数是把被数物体这一集合的元素与自然数列这一集合的元素,建立一一对应的过程。

它是一种有目的、有策略和有结果的操作活动,其结果以基数的形式呈现出来。

基数是指集合(一组相同属性的事物)中元素的多少,它是通过计数活动来确定的。

因此,在数学上,基数是集合论中刻画任意集合大小的一个概念。

二、学前儿童计数及基数认知能力的发展（一）2-3 岁儿童数概念及计数能力的发展2-3 岁阶段是儿童从感知事物阶段向数概念萌芽阶段迅速发展的时期，即从对事物的笼统感知到开始出现计数能力。

（二）3-4岁儿童数概念及计数能力的发展1.数概念的掌握离不开动作参与的计数活动2.经过数前集合感知经验的积累，3岁半左右的幼儿表现出对计数的兴趣，而且具备了学习计数的条件。

3.学前儿童掌握计数的过程。

（1）口头说数，俗称“顺口溜”，是口头按顺序说出自然数的能力。

（2）按物点数，即用手逐一指点物体，同时有顺序地说出数词，使说出的一个数词与手指点的物体一一对应。

（3）说出总数，指按物点数后，将说出的最后一个数词代表所数过的物体的总数量,即回答“一共是几个”。

（三）4-5岁儿童数概念及计数能力的发展1.较好地掌握了计数活动。

2.认数范围扩大到10,能做到按数取物。

3.初步感知、理解10以内相邻两数之间的关系。

4.有了初步的守恒能力（四）5-6岁儿童数概念及计数能力的发展1.很好地认识了10 以内数及相邻数。

所谓相邻数是指在自然数列中相邻三个数相差为1的关系的基础上,相邻的三个数存在着多1和少1的关系，即某数的前面一个数和后面一个数。

2.能按群计数按群计数就是计数时不以单个物体为单位，而是以数群(物体群)为单位。

三、计数的原则（一）一一对应的原则在进行计数活动中，儿童口中说的数词只能对应一个要数的物体。