5第五章第1讲函数依赖新
- 格式:ppt
- 大小:308.50 KB
- 文档页数:27



计算机四级考试《数据库工程师》重点知识:函数依赖计算机四级考试《数据库工程师》重点知识:函数依赖1、函数依赖:(1) 设R(U)为一关系模式,X和Y为属性全集U的子集,若对于R(U)的任意一个可能的关系r,r中不可能存在两个元组在X上的属性值相等,而在Y上的属性值不等,则称“X函数决定Y”或“Y函数依赖于X”,并记作XY,其中X称为决定因素,因为根据函数依赖定义,给定一个X,就能惟一决定一个Y。
(2) 这里讨论的函数关系与数学上的不同,是不能计算的,是一个关系中属性之间存在的依赖关系;它是一种语义范畴的概念,只能根据两个属性之间的语义来确定一个函数依赖是否存在。
2、完全与部分函数依赖:(1) 在关系模式R(U)中,如果XàY成立,并且对X的任何真子集X’不能函数决定Y,则称Y对X是完全函数依赖,被记作X---f---àY。
(2) 若XàY,但Y不完全函数依赖于X,则称Y对X是部分函数依赖,记作X--pàY;3、传递函数依赖:在关系R(U)模式中,如果X决定Y,(Y不属于X),Y不决定X,Y决定Z,则称Z对X传递函数依赖。
4、平凡与非平凡函数依赖:(1) 若X决定Y,但Y属于X,则称XàY是平凡函数依赖,否则称非平凡函数依赖;(2) 即平凡函数依赖,仅当其右边的属性集是左边属性集的子集时成立;(3) 非平凡函数依赖,仅当其右边的属性集至少有一个属性不属于左边有集合时成立;(4) 完全非平凡函数依赖:仅当其右边的属性集中属性都不在左边的集合时成立;5、码:(1) 在关系模式R(U)中,K为R的属性或属性组,若K函数决定A1.A2….An,则K为关系模式R的候选码,包含在候选码中的属性称为主属性,否则为非主属性;(2) 若一个关系的候选码不止一个,则选定其中一个作为关系R的主码;(3) 关系的码属性除了必须完全函数决定关系的所有其他属性外,还必须满足最小化规则,即在关系模式R(U)中,不存在一个K的.真子集能够函数决定R的其他属性。

函数依赖闭包⼀、函数依赖的逻辑蕴涵定义:设有关系模式R(U)及其函数依赖集F,如果对于R的任⼀个满⾜F的关系r函数依赖X→Y都成⽴,则称F逻辑蕴涵X→Y,或称X→Y可以由F推出。
例:关系模式 R=(A,B,C),函数依赖集F={A→B,B→C}, F逻辑蕴涵A→C。
证:设u,v为r中任意两个元组:若A→C不成⽴,则有u[A]=v[A],⽽u[C]≠v[C]⽽且A→B, B→C,知u[A]=v[A], u[B]=v[B], u[C]=v[C],即若u[A]=v[A]则u[C]=v[C],和假设⽭盾。
故F逻辑蕴涵A→C。
满⾜F依赖集的所有元组都函数依赖X→Y(X→Y不属于F集),则称F逻辑蕴涵X→Y(X→Y由F依赖集中所有依赖关系推断⽽出)⼆、Armstrong公理1、定理:若U为关系模式R的属性全集,F为U上的⼀组函数依赖,设X、Y、Z、W均为R的⼦集,对R(U,F)有:F1(⾃反性):若X≥Y(表X包含Y),则X→Y为F所蕴涵;(F1':X→X)F2(增⼴性): 若X→Y为F所蕴涵,则XZ→YZ为F所蕴涵;(F2':XZ→Y)F3(传递性): 若X→Y,Y→Z为F所蕴涵,则X→Z为F所蕴涵;F4(伪增性):若X→Y,W≥Z(表W包含Z)为F所蕴涵,则XW→YZ为F所蕴涵;F5(伪传性): 若X→Y,YW→Z为F所蕴涵, 则XW→Z为F所蕴涵;F6(合成性): 若X→Y,X→Z为F所蕴涵,则X→YZ为F所蕴涵;F7(分解性): 若X→Y,Z≤Y (表Z包含于Y)为F所蕴涵,则X→Z为F所蕴涵。
函数依赖推理规则F1∽F7都是正确的。
2、Armstrong公理:推理规则F1、F2、F3合称Armstrong公理;F4 ∽ F7可由F1、F2、F3推得,是Armstrong公理的推论部分。
三、函数依赖的闭包定义:若F为关系模式R(U)的函数依赖集,我们把F以及所有被F逻辑蕴涵的函数依赖的集合称为F的闭包,记为F+。

函数依赖关系
函数依赖是数据库设计的重要概念,它是一种表之间的逻辑关系,它把表的属性分成一组独立的变量,通过这种变量可以确定特定的元组。
函数依赖的概念源于一种实例确定的原则,也被称为属性依赖原理,说明特定属性可以确定表或元组中的其他属性。
换句话说,如果两个属性集之间存在函数依赖,那么一个属性集可以确定另一个属性集。
函数依赖主要用于设计数据库和表。
其目的是检测出违反三范式规范的字段,并对其进行消除和修改,以防止出现索引过大、查询效率低下等问题。
函数依赖可以用联合函数来表达,其格式为:A(X)→B(Y),表示的是X的值可以唯一确定Y的值。
另外,函数依赖也可以连贯推导出来,形式如:A→B,A,B→C,A,B→D,表示A的值可以唯一确定B,C,D的值。
函数依赖是一种实例确定的原则,也就是说,一个属性集可以确定另一个属性集。
函数依赖在数据库设计中具有重要作用,它可以检测出违反三范式规范的字段,并保持数据库的正确性和一致性。
此外,函数依赖可以促进查询设计,帮助我们理解不同的表之间的关系,以及表之间变量的相互依赖。

函数依赖和多值依赖一、函数依赖函数依赖是关系数据库中最基本的依赖关系之一,它描述了一个属性集合中某些属性对其他属性的决定作用。
在一个关系模式R中,如果对于R的任意一组元组t1和t2,若t1和t2在属性集合X上取值相同,则它们在属性集合Y上取值也相同,那么我们称Y对X有函数依赖。
可以用X→Y来表示。
二、多值依赖多值依赖是指在一个关系模式R中,存在这样两个属性集合X和Y (其中X和Y不为空),满足对于R的任意一组元组t1和t2,如果它们在X上取值相同,则它们在除去X后剩余的属性集合Z上必须取相同的所有可能值。
可以用X→→Z来表示。
三、函数依赖与多值依赖的区别函数依赖描述了一个属性对其他属性的决定作用,而多值依赖描述了两个或更多个非主属性之间的关系。
四、实现函数依赖与多值依赖实现函数依赖和多值依赖需要进行以下步骤:1.确定实体及其属性。
2.识别实体间联系及其类型。
3.设计ER图并转换为关系模式。
4.检查关系模式的范式,消除不符合范式的关系模式。
5.对于存在函数依赖和多值依赖的关系模式,进行分解。
五、分解函数依赖分解函数依赖需要进行以下步骤:1.将原始关系模式拆分成两个或多个新的关系模式,每个新的关系模式都包含原始属性集合中的一部分属性。
2.为新的关系模式定义主键和外键,以确保它们之间有正确的联系。
3.使用连接操作来重新组合这些新的关系模式。
六、分解多值依赖分解多值依赖需要进行以下步骤:1.将原始关系模式拆分成两个或多个新的关系模式,每个新的关系模式都包含原始属性集合中的一部分属性。
2.为新的关系模式定义主键和外键,以确保它们之间有正确的联系。
3.在第二个新建立一个独立表格,并把非主属性从第一个表格中转移到第二个表格中。
4.使用连接操作来重新组合这些新建立表格。
七、总结在设计数据库时,应该注意到函数依赖和多值依赖。
如果发现存在函数依赖或多值依赖,则应该采取相应的措施来分解它们,以确保数据库的正常运行。
函数依赖(理论及举例)教你如何理解函数依赖一、函数依赖的概念函数依赖:函数依赖就是讨论一个数据表(关系)中属性值之间所存在的函数关系。
函数是一种数学中的概念,被引入到数据库中对数据的联系进行分析。
在一个关系中,属性相当于数学上的变量,属性的域相当于变量的取值范围,属性在一个元组上的取值相当于属性变量的当前值。
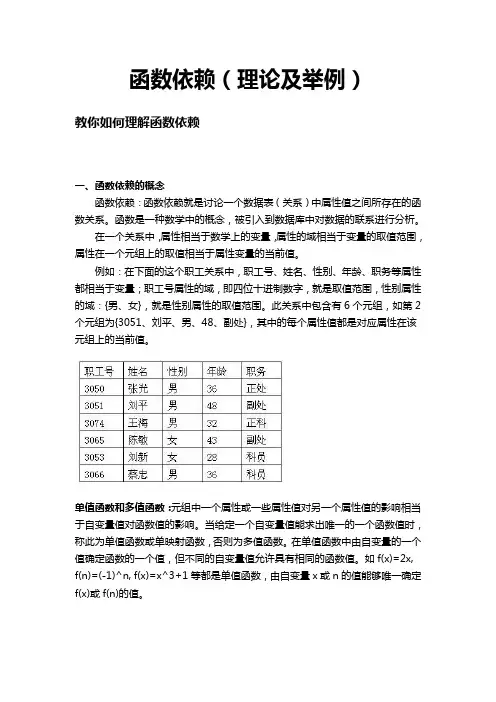
例如:在下面的这个职工关系中,职工号、姓名、性别、年龄、职务等属性都相当于变量;职工号属性的域,即四位十进制数字,就是取值范围,性别属性的域:{男、女},就是性别属性的取值范围。
此关系中包含有6个元组,如第2个元组为{3051、刘平、男、48、副处},其中的每个属性值都是对应属性在该元组上的当前值。
单值函数和多值函数:元组中一个属性或一些属性值对另一个属性值的影响相当于自变量值对函数值的影响。
当给定一个自变量值能求出唯一的一个函数值时,称此为单值函数或单映射函数,否则为多值函数。
在单值函数中由自变量的一个值确定函数的一个值,但不同的自变量值允许具有相同的函数值。
如f(x)=2x, f(n)=(-1)^n, f(x)=x^3+1等都是单值函数,由自变量x或n的值能够唯一确定f(x)或f(n)的值。
属性的单值函数决定(依赖):在一个关系中,若一个或一组属性的值对另一个或一组属性值起到决定性的作用,则称为单值函数决定(依赖)。
如上表中职工号的值就能够函数决定其余每个属性的值,也就是说,当职工号给定后,其他每个属性的值就跟着唯一地确定了。
如假定职工号为3074,则他的姓名必定是王海,性别必定为男,年龄必定为32岁,职务必定为正科。
这就叫做职工号能够分别单值函数决定姓名、性别和年龄属性,反过来,可以说姓名、性别和年龄等属性单值函数依赖于职工号属性。
二、函数依赖的定义定义:设一个关系为R(U),X和Y为属性集U上的子集,若对于X上的每个值都有Y上的一个唯一值与之对应,则称X和Y具有函数依赖关系,并称X 函数决定Y,或称Y函数依赖于X,记作X→Y,称X为决定因素。

函数依赖及范式函数依赖基本概念:•函数依赖:FD(function dependency),设有关系模式R(U),X,Y是U的子集,r 是R的任一具体关系,如果对r的任意两个元组t1,t2,由t1[X]=t2[X]导致t1[Y]=t2[Y], 则称X 函数决定Y,或Y函数依赖于X,记为X→Y。
X→Y为模式R的一个函数依赖。
•部分函数依赖:即局部依赖,对于一个函数依赖W→A,如果存在X W(X包含于W)有X→A成立,那么称W→A是局部依赖,否则称W→A为完全函数依赖。
•传递依赖:在关系模式中,如果Y→X,X→A,且X Y(X不决定Y),A X(A不属于X),那么称Y→A是传递依赖。
•函数依赖集F的闭包F+: 被逻辑蕴涵的函数依赖的全体构成的集合,称为F的闭包(clo sure),记为F+。
•最小依赖集:如果函数集合F满足以下三个条件(1)F中每个函数依赖的右部都是单属性;(2) F中的任一函数依赖X→A,其F-{X→A}与F是不等价的;(3)F中的任一函数依赖X→A,Z为X的子集,(F-{X→A})∪{Z→A}与F不等价。
则称F为最小函数依赖集合,记为Fmin。
函数依赖的公理系统:设有关系模式R(U),X,Y,Z,W均是U的子集,F是R上只涉及到U中属性的函数依赖集,推理规则如下:•自反律:如果Y X U,则X→Y在R上成立。
•增广律:如果X→Y为F所蕴涵,Z U,则XZ→YZ在R上成立。
(XZ表示X∪Z,下同) •传递律:如果X→Y和Y→Z在R上成立,则X→Z在R上成立。
以上三条为Armstrong公理系统•合并律:如果X→Y和X→Z成立,那么X→YZ成立。
•伪传递律:如果X→Y和WY→Z成立,那么WX→Z成立。
•分解律:如果X→Y和Z Y成立,那么X→Z成立。
这三条为引理注意:•函数依赖推理规则系统(自反律、增广律和传递律)是完备的。
•由自反律所得到的函数依赖均是平凡的函数依赖。
四种范式的含义:•如果某个数据库模式都是第一范式的,则称该数据库模式是属于第一范式的数据库模式。


函数依赖2.1、属性间的联系实体间的联系有两类:一类是实体与实体之间的联系;另一类是实体内部各属性间的联系。
属性间的联系可分为以下三类:(1)一对一联系(1∶1)以职工模式为例:职工(职工号,姓名,职称,部门)。
如果该企业(或单位)中职工无重名,则属性职工号与姓名之间是1∶1联系。
一个职工号唯一地决定一个姓名,一个姓名也可决定唯一的职工号。
设X、Y是关系R的两个属性(集)。
如果对于X中的任一具体值,Y中至多有一个值与之对应,且反之亦然,则称X、Y两属性间是一对一联系。
(2)一对多联系(1∶ m)在职工模式中,职工号和职称间是一对多联系。
一个职工号只对应一种职称(如胡一民只能对应工程师),但一种职称却可对应多个职工号(如工程师可对应多名职工)。
设X、Y是关系R的两个属性(集)。
如果对于X中的任一具体值,Y中至多有一个值与之对应,而Y中的一个值却可以和X中的n个值相对应,则称Y对X是一对多联系。
(3)多对多联系(m∶ m)在职工模式中,职称和部门之间是多对多联系。
一种职称可分布在多个部门中(如每一个部门中均可有工程师),而一个部门中也可有多个职称。
设X、Y是关系R的两个属性(集)。
如果对于X中的任一具体值,Y中有m个值与之对应,而Y中的一个值也可以和X中的n个值相对应,则称Y对X是多对多联系。
上述属性间的三种联系实际上是属性值之间相互依赖又相互制约的反映,称为属性间的数据依赖。
数据依赖共有三种:函数依赖(FunctionalDependency,简称FD)、多值依赖(Multiva-luedDependency,简称MVD)和连接依赖(JoinDependency,简称JD),其中最重要的是函数依赖和多值依赖。
2.2、函数依赖函数依赖是属性之间的一种联系。
假设给定一个属性的值,就可以唯一确定(查到)另一个属性的值。
定义:所谓函数依赖是指在关系R中,X、Y为R的两个属性或属性组,如果对于R的任一关系r都存在:对于X的每一个具体值,Y 都只有一个具体值与之对应,则称属性Y函数依赖于属性X。
数据库函数依赖和范式总结1 函数依赖1.1 定义:一个集合R(U,F),U为属性全集,F为函数依赖集合。
F中存在着{Xi->Yi...};对于每个X都存在着一个Y与之唯一对应。
意思就是相当于X为主键,Y由主键决定。
比如一个学生他的学号相当于X,而他的姓名与年龄这些其他信息相当于Y。
但是X有时候并不是一个值,比如一个学生他的成绩需要有两个属性才能知道他的成绩,学号+课程号->成绩1.2 平凡函数依赖与非平凡函数依赖平时我们主要讨论的是非平凡函数依赖。
平凡函数依赖概念:Y集合属性属于X集合属性的子集非平凡函数则相反1.3 逻辑蕴涵(为后面求闭包做好基础)X,Y为属性集合U的子集,且X->Y不存在于F中。
即我们需要通过F中的函数依赖推出X->Y称为函数依赖。
而所有函数依赖的集合则称为闭包1.4 函数依赖的推理规则(就是求函数依赖的逻辑蕴涵)1.4.1 几个公理1.4.1.1 公理一(自反律):Y属于X的子集,则X->Y 数学公式描述 Y?X?U1.4.1.2 公理二(增广律):X->Y成立,Z?U也成立,则 XZ?YZ1.4.1.3 公理三(传递律):X->Y成立,Y->Z成立,则 X->Z1.4.2 公理的推广1.4.2.1 推广一(合并律):X->Y,X->Z,则X->YZ1.4.2.2 推广二(伪传递律):X->Y,YW->Z,则XW->Z(证明只需要在XY两边*W)1.4.2.3 推广三(分解律):X->Y成立,Z?Y,则 X->Z1.4.2.4 推广四(复合律):X->Y,W->Z,则XW->YZ1.5 完全函数依赖与部分函数依赖(范式中基础知识)X->Y的集合中,若X的任一真子集x都能 x->Y则为部分函数依赖,若不能则的完全函数依赖,如果X没有真子集则也称为完全函数依赖。
简述函数依赖的定义函数依赖是数据库中用来描述关系模式中属性之间的关系的概念。
在关系型数据库中,数据以表的形式组织,表中的每一列都是一个属性,属性之间可能存在依赖关系。
函数依赖就是描述属性之间的依赖关系,它定义了在一个关系中,一个或多个属性的取值决定了其他属性的取值。
在关系模型中,函数依赖的定义包括两个方面:左侧和右侧。
左侧是决定其他属性取值的属性集合,右侧是由左侧属性决定的属性集合。
一个函数依赖可以表示为X → Y,其中 X 是左侧属性的集合,Y 是右侧属性的集合。
这个函数依赖的意义是,给定X 的值,就可以唯一确定 Y 的值。
换句话说,对于每一个 X 的值,关系中的其他属性的取值都是唯一确定的。
函数依赖的定义可以进一步扩展,引入部分函数依赖和传递函数依赖的概念。
部分函数依赖是指在函数依赖X → Y 中,如果 Y 不依赖于 X 的任何真子集,则称X → Y 是部分函数依赖。
也就是说,如果去掉X 的任何一个属性,Y 的取值将无法确定。
传递函数依赖是指在函数依赖X → Y 和Y → Z 成立的情况下,可以推导出X → Z 的依赖关系。
也就是说,如果存在X → Y 和 Y → Z,那么可以推出X → Z。
函数依赖的概念在数据库设计中起着重要的作用。
通过分析函数依赖,可以帮助我们识别出关系模式中的冗余数据,避免数据冗余和不一致。
在数据库设计中,我们希望尽量消除冗余数据,提高数据的一致性和完整性。
举例来说,假设有一个关系模式 R(A, B, C, D),其中 A 是主键。
如果存在函数依赖A → B 和B → C,那么我们可以推导出A → C 和A → D 的函数依赖关系。
在这个例子中,属性 A 的值唯一决定了属性B、C 和D 的值,因此可以说属性B、C 和D 是函数依赖于A 的。
在数据库设计中,我们可以利用函数依赖的概念进行关系模式的分解和规范化。
通过合理地分解和规范化关系模式,可以提高数据库的性能和数据的一致性。
函数依赖蕴含于1. 什么是函数依赖在数据库中,函数依赖指的是一张关系表中,一个或一组属性的取值可以唯一地确定另一个或另一组属性的取值。
比如,基于学生信息表中的学号,我们可以确定每个学生的姓名、性别、出生年月等基本信息。
在这里,学号就是决定属性,而姓名、性别、出生年月等基本信息就是被依赖属性。
我们可以用一个函数依赖图(依赖关系图)表示上述依赖关系。
比如,可以用一个箭头从学号指向姓名,表示学号决定姓名,也可以用一条线从学号连接到姓名,线的末端标注“学号→ 姓名”。
2. 函数依赖的种类函数依赖可以分为以下两种:2.1. 完全函数依赖完全函数依赖指的是某个属性集合中的每一个属性都不能被包含在另一个属性集中,否则就不是完全函数依赖。
比如,如果学号和课程编号可以唯一地决定成绩,那么成绩就是学号和课程编号的完全函数依赖。
2.2. 部分函数依赖部分函数依赖指的是某个属性集合中的一部分属性无法确定另一个属性的取值,必须要使用该属性集合中其他属性才能唯一地确定。
比如,如果学号能够唯一决定姓名,但学号和电话号码的任意一个都无法唯一决定姓名,那么就出现了学号和电话号码的部分函数依赖。
3. 函数依赖的蕴含关系函数依赖的蕴含关系指的是如果一个表中存在若干个函数依赖,则这些函数依赖中的任意一个依赖另一个依赖的属性,则这些函数依赖就可以归纳为一个公共的、更大的函数依赖。
这个概念非常重要,因为它可以被用来优化数据库模式,减少数据冗余。
比如,一个学生信息表可能有如下函数依赖:学号→ 姓名学号→ 性别学号, 课程编号→ 成绩在这个依赖关系图中,学号决定了姓名和性别,但学号和课程编号才能同时决定成绩。
这时候,我们可以归纳出一个更大的函数依赖:学号, 课程编号→ 姓名, 性别, 成绩按照这个函数依赖,我们不需要存储姓名和性别两个属性,因为它们可以从学号和课程编号推导出来。
同样的,如果我们只需要列出学号、课程编号和成绩,那么这个新的函数依赖也可以被归纳为:学号, 课程编号→ 成绩4. 如何维护函数依赖为了保持数据库中的数据一致性,我们必须准确维护函数依赖关系。
函数依赖的定义
如果对于函数a, b, c,……我们称它们之间存在依赖关系,那么这种依赖关系就叫做函数依赖关系。
如果说依赖的对象是函数,依赖的关系叫做函数依赖关系,而依赖的形式称为函数依赖。
依赖性主要体现在函数依赖的两个方面,一是在同一个函数上可以定义多个相互依赖的函数;二是依赖的函数或者依赖的关系可以依次出现在不同的函数上或者不同的函数关系上。
1、函数依赖关系。
依赖关系的实例是一些很普通的集合或者是映射:所有的实数集合n(n≥1),复数集合(c∈S)都是同构的。
同构关系是由函数依赖关系衍生出来的。
由定义可知,若M为一个非空集合,而G是一个集合,如果满足则它们之间存在着函数依赖关系。
而同时有三个元素的集合也是同构的。
我们常常把复数的表示法和几何表示法结合起来使用。
- 1 -。