第5章 公式与函数的使用
- 格式:ppt
- 大小:1.85 MB
- 文档页数:45




三角函数与解三角形公式总结【预备知识点】一、任意角与弧度制(一)任意角1.任意角的概念:规定一条射线绕其端点任意方向旋转所形成的角。
2.任意角的分类:(1)正角:规定一条射线绕其端点逆时针方向旋转所形成的角。
(2)负角:规定一条射线绕其端点顺时针方向旋转所形成的角。
(3)零角:规定一条射线绕其端点无任意方向旋转所形成的角,始边与终边重合的角。
口诀:正逆负顺零重合3.相等角、相反角与角的运算(1)相等角:旋转方向相同且旋转量相等。
(2)相反角:旋转方向相反且旋转量相等。
(3)角的运算:线性加减运算与数乘运算。
4.常见误区:(1)锐角是第一象限角,但是第一象限角不一定是锐角,因为有周期。
例如420°。
(2)钝角是第二象限角,但是第二象限角不一定是钝角,因为有周期。
例如495°。
(3)直角不是任意象限角,属于y轴的特殊角。
(4)平角、周角属于轴线角,它不属于任何一个象限角。
(二)弧度制1.弧长公式及其意义(1)弧长公式:l=nπr180⟺lr=n∗π180=|α|⟺l=|α|r(2)弧长公式的意义:(i)圆心角α所对的弧长与半径r的比值,只与α大小有关。
(ii)弧长长度等于半径长的圆弧所对的圆心角叫做1弧度的角,用rad表示,读作弧度。
其中rad可省略。
(3)一般地,正角的弧度数是正数,零角的弧度数是0,负角的弧度数是一个负数。
2.角度制与弧度制的互换依据:180°=π rad{1°=π180rad≈0.01745 rad 1 rad=(180π)°≈57.30°=57°18′(三)常见的角度制与弧度制互换表示二、三角函数常用特殊值【大重点,熟练背诵】【必考知识点】一、三角函数概念(1)定义式【熟记理解】(2)同角三角函数的基本关系【大重点题型:化弦为切经常用到,结合诱导公式与恒等变换】(i)平方关系【重点记第一个】sin2x+cos2x=11+cot2x=csc2x1+tan2x=sec2x(ii)商数关系【重点记第一个】tanx=sinx cosxcotx=cosx sinx(iii)倒数关系tanx∗cotx=1sinx∗cscx=1cosx∗secx=1(3)三角函数在各象限的符号【大重点并背诵】二、诱导公式【大重点,以下表格全背】诱导公式的基本思路【以第1组~第4组为例】:(1)首先,任意负角的三角函数转化成任意正角的三角函数【用公式3或1】(2)其次,任意正角的三角函数转化成0∼2π的三角函数【用公式1】(3)最后,0∼2π的三角函数转化成锐角三角函数【用公式2或4】三、三角恒等变换【大重点,所有公式都要背】1.两角和与差的正弦、余弦、正切Cα−β:cos(α−β)=cosα∗cosβ+sinα∗sinβCα+β:cos(α+β)=cosα∗cosβ−sinα∗sinβSα−β:sin(α−β)=sinα∗cosβ−cosα∗sinβSα+β:sin(α+β)=sinα∗cosβ+cosα∗sinβTα−β:tan(α−β)=tanα−tanβ1+tanα∗tanβTα+β:tan(α+β)=tanα+tanβ1−tanα∗tanβ扩展:三角和公式Cα+β+γ:cos(α+β+γ)=cosα∗cosβ∗cosγ−cosα∗sinβ∗sinγ−sinα∗cosβ∗sinγ−sinα∗sinβ∗cosγSα+β+γ:sin(α+β+γ)=sinα∗cosβ∗cosγ+cosα∗sinβ∗cosγ+cosα∗cosβ∗sinγ−sinα∗sinβ∗sinγTα+β+γ:tan(α+β+γ)=tanα+tanβ+tanγ−tanα∗tanβ∗tanγ1−tanα∗tanβ−tanα∗tanγ−tanβ∗tanγ2.二倍角的正弦、余弦、正切C2α: cos2α=cos2α−sin2α=1−2sin2α=2cos2α−1; cos2α=1+cos2α2,sin2α=1−cos2α2S2α: sin2α=2sinα∗cosαT2α: tan2α=2tanα1−tan2α扩展1:半角公式Cα2: cosα2=±√1+cosα2Sα2: sinα2=±√1−cosα2Tα2: tanα2=sinα1+cosα=1−cosαsinα=±√1−cosα1+cosα注意:正负由α2所在的象限决定!其中Cα: cosα=cos2α2−sin2α2=1−2sin2α2=2cos2α2−1=1−tan2α21+tan2α2Sα: sinα=2sin α2∗cosα2=2∗tanα21+tan2α2Tα:tanα=2∗tanα2 1−tan2α2扩展2:三倍角公式S3α: sin3α=3sinα−4sin3α=4sinα∗sin(π3−α)∗sin(π3+α)C3α: cos3α=4cos3α−3cosα=4cosα∗cos(π3−α)∗cos(π3+α)T3α: tan3α=3tanα−tan3α1−3tan3α=tanα∗tan(π3−α)∗tan(π3+α)扩展3:四倍角公式S4α: sin4α=−4∗[cosα∗sinα∗(2sin2α−1)]C4α: cos4α=1−8∗cos2α∗sin2αT4α: tan4α=4tanα−4tan3α1−6tan2α+tan4α扩展4:五倍角公式S5α: sin5α=16sin5α−20sin3α+5sinαC5α: cos5α=16cos5α−20cos3α+5cosαT5α: tan5α=5−10tan2α+tan4α1−10tan2α+5tan4α3.和差化积公式sin α+sin β=2sin α+β2∗cosα−β2sin α−sin β=2cos α+β2∗sinα−β2cos α+cos β=2cos α+β2∗cosα−β2cos α−cos β=−2sin α+β2∗sinα−β2tan α+tan β=sin(α+β) cosα∗cosβtan α−tan β=sin(α−β) cosα∗cosβcot α+cot β=sin(α+β) sinα∗sinβcot α−cot β=−sin(α−β) sinα∗sinβtan α+cot β=cos(α−β) cosα∗sinβtan α−cot β=−cos(α+β) cosα∗sinβsin2α−sin2β=sin(α+β)∗sin(α−β)cos2α−cos2β=−sin(α+β)∗sin(α−β)sin2α−cos2β=−cos(α+β)∗cos(α−β)cos2α−sin2β=cos(α+β)∗cos(α−β)记忆口诀:同名和差三角积,(sin α±sin β或cos α±cos β:等式左边只有同是正弦或同是余弦才可以相加减。


第1课时公式二、公式三和公式四学习目标核心素养1。
了解公式二、公式三和公式四的推导方法.2.能够准确记忆公式二、公式三和公式四.(重点、易混点)3.掌握公式二、公式三和公式四,并能灵活应用.(难点)1.借助公式进行运算,培养数学运算素养.2.通过公式的变形进行化简和证明,提升逻辑推理素养。
1.公式二(1)角π+α与角α的终边关于原点对称.如图所示.(2)公式:sin(π+α)=-sin_α,cos(π+α)=-cos_α,tan(π+α)=tan_α.2.公式三(1)角-α与角α的终边关于x轴对称.如图所示.(2)公式:sin(-α)=-sin_α,cos(-α)=cos_α,tan(-α)=-tan_α.3.公式四(1)角π-α与角α的终边关于y轴对称.如图所示.(2)公式:sin(π-α)=sin_α,cos(π-α)=-cos_α,tan(π-α)=-tan_α。
思考:(1)诱导公式中角α只能是锐角吗?(2)诱导公式一~四改变函数的名称吗?提示:(1)诱导公式中角α可以是任意角,要注意正切函数中要求α≠kπ+π2,k∈Z.(2)诱导公式一~四都不改变函数名称.1.如果α,β满足α+β=π,那么下列式子中正确的个数是()①sin α=sin β;②sin α=-sin β;③cos α=-cos β;④cos α=cos β;⑤tan α=-tan β.A.1 B.2 C.3 D.4C[因为α+β=π,所以sin α=sin(π-β)=sin β,故①正确,②错误;cos α=cos(π-β)=-cos β,故③正确,④错误;tan α=tan(π-β)=-tan β,⑤正确.故选C。
]2.tan错误!等于()A.-错误!B。
错误!C.-错误! D.错误!C[tan错误!=tan错误!=tan错误!=tan错误!=-tan错误!=-错误!.]3.已知tan α=3,则tan(π+α)=________。



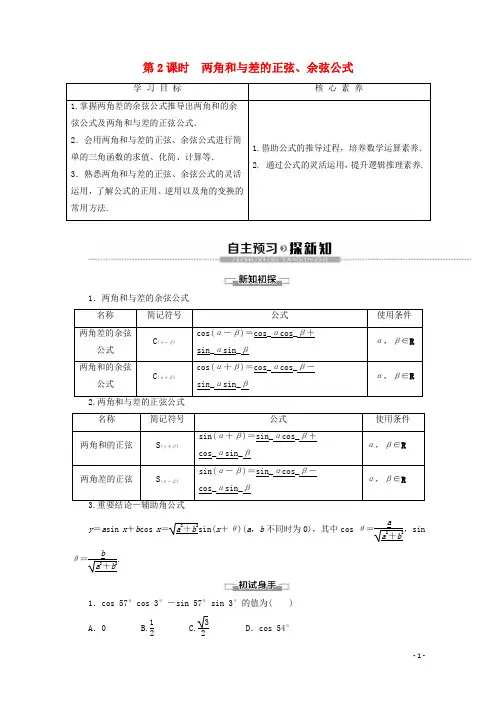
第2课时 两角和与差的正弦、余弦公式学 习 目标核 心 素 养1.掌握两角差的余弦公式推导出两角和的余弦公式及两角和与差的正弦公式. 2.会用两角和与差的正弦、余弦公式进行简单的三角函数的求值、化简、计算等. 3.熟悉两角和与差的正弦、余弦公式的灵活运用,了解公式的正用、逆用以及角的变换的常用方法.1.借助公式的推导过程,培养数学运算素养.2. 通过公式的灵活运用,提升逻辑推理素养.1.两角和与差的余弦公式 名称 简记符号 公式使用条件两角差的余弦公式 C (α-β)cos(α-β)=cos_αcos_β+sin_αsin_βα,β∈R两角和的余弦公式C (α+β) cos(α+β)=cos_αcos_β-sin_αsin_βα,β∈R名称 简记符号 公式使用条件两角和的正弦S (α+β)sin(α+β)=sin_αcos_β+cos_αsin_βα,β∈R两角差的正弦 S (α-β) sin(α-β)=sin_αcos_β-cos_αsin_βα,β∈Ry =a sin x +b cos x =a 2+b 2sin(x +θ)(a ,b 不同时为0),其中cos θ=a a 2+b 2,sinθ=b a 2+b 2.1.cos 57°cos 3°-sin 57°sin 3°的值为( ) A .0 B.12 C.32D .cos 54°B [原式=cos(57°+3°)=cos 60°=12.]2.sin 245°sin 125°+sin 155°sin 35°的值是( ) A .-32B .-12C.12D.32B [∵sin 245°=sin(155°+90°)=cos 155°, sin 125°=sin(90°+35°)=cos 35°,∴原式=cos 155°cos 35°+sin 155°sin 35°=cos(155°-35°)=cos 120°=-12.] 3.若cos α=-35,α是第三象限的角,则sin ⎝ ⎛⎭⎪⎫α-π4=______. -210 [∵cos α=-35,α是第三象限的角, ∴sin α=-1-cos 2α=-45,∴sin ⎝⎛⎭⎪⎫α-π4=22sin α-22cos α=22×⎝ ⎛⎭⎪⎫-45-22×⎝ ⎛⎭⎪⎫-35=-210.],给角求值问题【例1】 (1)cos70°sin 50°-cos 200°sin 40°的值为( )A .-32 B .-12 C.12 D.32(2)若θ是第二象限角且sin θ=513,则cos(θ+60°)=________.(3)求值:(tan 10°-3)cos 10°sin 50°.(1)D (2)-12+5326 [(1)∵cos 200°=cos(180°+20°)=-cos 20°=-sin70°,sin 40°=cos 50°,∴原式=cos 70°sin 50°-(-sin 70°)cos 50° =sin(50°+70°)=sin 120°=32.(2)∵θ是第二象限角且sin θ=513,∴cos θ=-1-sin 2θ=-1213,∴cos(θ+60°)=12cos θ-32sin θ=12×⎝ ⎛⎭⎪⎫-1213-32×513=-12+5326.] (3)[解] 原式=(tan 10°-tan 60°)cos 10°sin 50°=⎝ ⎛⎭⎪⎫sin 10°cos 10°-sin 60°cos 60°cos 10°sin 50°=sin (-50°)cos 10°cos 60°·cos 10°sin 50°=-2.]解决给角求值问题的策略(1)对于非特殊角的三角函数式求值问题,一定要本着先整体后局部的基本原则,如果整体符合三角公式的形式,则整体变形,否则进行各局部的变形.(2)一般途径有将非特殊角化为特殊角的和或差的形式,化为正负相消的项并消项求值,化分子、分母形式进行约分,解题时要逆用或变用公式.提醒:在逆用两角的和与差的正弦和余弦公式时,首先要注意结构是否符合公式特点,其次注意角是否满足要求.1.化简求值:(1)sin 50°-sin 20°cos 30°cos 20°;(2)sin(θ+75°)+cos(θ+45°)-3cos(θ+15°). [解] (1)原式=sin (20°+30°)-sin 20°cos 30°cos 20°=sin 20°cos 30°+cos 20°sin 30°-sin 20°cos 30°cos 20°=cos 20°sin 30°cos 20°=sin 30°=12.(2)设α=θ+15°,则原式=sin(α+60°)+cos(α+30°)-3cos α=⎝ ⎛⎭⎪⎫12sin α+32cos α+⎝ ⎛⎭⎪⎫32cos α-12sin α-3cos α=0.给值求值、求角问题【例2】 (1)已知P ,Q 是圆心在坐标原点O 的单位圆上的两点,且分别位于第一象限和第四象限,点P 的横坐标为45,点Q 的横坐标为513,则cos∠POQ =________.(2)已知cos α=55,sin(α-β)=1010,且α,β∈⎝⎛⎭⎪⎫0,π2.求:①cos(2α-β)的值;②β的值.[思路点拨] (1)先由任意角三角函数的定义求∠xOP 和∠xOQ 的正弦、余弦值,再依据∠POQ =∠xOP +∠xOQ 及两角和的余弦公式求值.(2)先求sin α,cos(α-β),依据2α-β=α+(α-β)求cos(2α-β).依据β=α-(α-β)求cos β再求β.(1)5665 [由题意可得,cos∠xOP =45, 所以sin∠xOP =35.再根据cos∠xOQ =513,可得sin∠xOQ =-1213,所以cos∠POQ =cos(∠xOP +∠xOQ )=cos∠xOP ·cos∠xOQ -sin∠xOP ·sin∠xOQ =45×513-35×⎝ ⎛⎭⎪⎫-1213=5665.] (2)[解] ①因为α,β∈⎝⎛⎭⎪⎫0,π2,所以α-β∈⎝ ⎛⎭⎪⎫-π2,π2,又sin(α-β)=1010>0,所以0<α-β<π2,所以sin α=1-cos 2α=255,cos(α-β)=1-sin 2(α-β)=31010,cos(2α-β)=cos[α+(α-β)]=cos αcos(α-β)-sin αsin(α-β) =55×31010-255×1010=210. ②cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β) =55×31010+255×1010=22, 又因为β∈⎝⎛⎭⎪⎫0,π2,所以β=π4.给值求值问题的解题策略在解决此类题目时,一定要注意已知角与所求角之间的关系,恰当地运用拆角、拼角技巧,同时分析角之间的关系,利用角的代换化异角为同角,具体做法是:(1)当条件中有两角时,一般把“所求角”表示为已知两角的和或差. (2)当已知角有一个时,可利用诱导公式把所求角转化为已知角.2.已知锐角α,β满足cos α=255,sin(α-β)=-35,求sin β的值.[解] 因为α,β是锐角,即0<α<π2,0<β<π2,所以-π2<α-β<π2,因为sin(α-β)=-35<0,所以cos(α-β)=45,因为cos α=255,所以sin α=55,所以sin β=sin[α-(α-β)]=sin αcos(α-β)-cos αsin(α-β)=55×45+255×35=255. 辅助角公式的应用[探究问题]1.能否将函数y =sin x +cos x (x ∈R )化为y =A sin(x +φ)的形式⎝ ⎛⎭⎪⎫|φ|∈⎝ ⎛⎭⎪⎫0,π2?提示:能.y =sin x +cos x =2sin ⎝⎛⎭⎪⎫x +π4.2.如何推导a sin x +b cos x =a 2+b 2sin(x +φ)⎝⎛⎭⎪⎫tan φ=b a 公式. 提示:a sin x +b cos x=a 2+b 2⎝ ⎛⎭⎪⎫a a 2+b 2sin x +b a 2+b 2cos x ,令cos φ=a a 2+b2,sin φ=b a 2+b 2,则a sin x +b cos x =a 2+b 2(sin x cos φ+cos x sin φ)=a 2+b 2sin(x +φ)(其中φ角所在象限由a ,b 的符号确定,φ角的值由tan φ=ba确定,或由sin φ=ba 2+b2和cos φ=a a 2+b 2共同确定).【例3】 (1)sin π12-3cos π12=________.(2)已知f (x )=3sin x -cos x ,求函数f (x )的周期,值域,单调递增区间.[思路点拨] 解答此类问题的关键是巧妙构建公式C (α-β)、C (α+β)、S (α-β)、S (α+β)的右侧,逆用公式化成一个角的一种三角函数值.(1)-2 [原式=2⎝ ⎛⎭⎪⎫12sin π12-32cos π12.法一:(化正弦)原式=2⎝ ⎛⎭⎪⎫cos π3sin π12-sin π3cos π12=2⎝ ⎛⎭⎪⎫sin π12cos π3-cos π12sin π3=2sin ⎝⎛⎭⎪⎫π12-π3=2sin ⎝ ⎛⎭⎪⎫-π4=- 2. 法二:(化余弦)原式=2⎝ ⎛⎭⎪⎫sin π6sin π12-cos π6cos π12=-2⎝ ⎛⎭⎪⎫cos π6cos π12-sin π6sin π12=-2cos ⎝ ⎛⎭⎪⎫π6+π12=-2cos π4=- 2.](2)[解] f (x )=3sin x -cos x=2⎝ ⎛⎭⎪⎫sin x ·32-cos x ·12 =2⎝⎛⎭⎪⎫sin x cos π6-cos x sin π6 =2sin ⎝⎛⎭⎪⎫x -π6, ∴T =2πω=2π,值域[-2,2].由-π2+2k π≤x -π6≤π2+2k π,得递增区间⎣⎢⎡⎦⎥⎤-π3+2k π,2π3+2k π,k ∈Z .1.若将例3(2)中函数改为f (x )=-sin x +3cos x ,其他条件不变如何解答? [解] f (x )=-sin x +3cos x =232cos x -12sin x =2cos ⎝⎛⎭⎪⎫x +π6,∴T =2π,值域为[-2,2],由-π+2k π≤x +π6≤2k π,得递增区间⎣⎢⎡⎦⎥⎤-7π6+2k π,-π6+2k π,k ∈Z .2.若将例3(2)中函数改为f (x )=m sin x +m cos x ,其中m >0,其他条件不变,应如何解答?[解] f (x )=m sin x +m cos x =2m sin ⎝⎛⎭⎪⎫x +π4,∴T =2π,值域为[-2m ,2m ],由-π2+2k π≤x +π4≤π2+2k π,得递增区间⎣⎢⎡⎦⎥⎤-3π4+2k π,π4+2k π,k ∈Z .辅助角公式及其运用(1)公式形式:公式a sin α+b cos α=a 2+b 2sin (α+φ)(或a sin α+b cos α=a 2+b2cos (α-φ))将形如a sin α+b cos α(a ,b 不同时为零)的三角函数式收缩为同一个角的一种三角函数式.(2)形式选择:化为正弦还是余弦,要看具体条件而定,一般要求变形后角α的系数为正,这样更有利于研究函数的性质.提醒:在使用辅助角公式时常因把辅助角求错而致误.1.两角和与差公式可以看成是诱导公式的推广,诱导公式可以看成两角和差公式的特例,例如:sin ⎝⎛⎭⎪⎫3π2-α=sin 3π2·cos α-cos 3π2sin α=-cos α.2.使用和差公式时不仅要会正用,还要能够逆用公式,如化简sin βcos(α+β)-cosβsin(α+β)时,不要将cos(α+β)和sin(α+β)展开,而应采用整体思想,作如下变形:sin βcos(α+β)-cos βsin(α+β)=sin[β-(α+β)]=sin(-α)=-sin α. 3.运用和差公式求值、化简、证明时要注意灵活进行三角变换,有效地沟通条件中的角与问题结论中的角之间的联系,选用恰当的公式快捷求解.1.思考辨析(1)两角和与差的正弦、余弦公式中的角α,β是任意的.( ) (2)存在α,β∈R ,使得sin(α-β)=sin α-sin β成立.( ) (3)对于任意α,β∈R ,sin(α+β)=sin α+sin β都不成立.( ) (4)sin 54°cos 24°-sin 36°sin 24°=sin 30°.( ) [提示] (1)正确.根据公式的推导过程可得.(2)正确.当α=45°,β=0°时,sin(α-β)=sin α-sin β.(3)错误.当α=30°,β=-30°时,sin(α+β)=sin α+sin β成立. (4)正确.因为sin 54°cos 24°-sin 36°sin 24° =sin 54°cos 24°-cos 54°sin 24°=sin(54°-24°) =sin 30°,故原式正确.[答案] (1)√ (2)√ (3)× (4)√ 2.化简2cos x -6sin x 等于( )A .22sin ⎝ ⎛⎭⎪⎫π6+xB .22cos ⎝ ⎛⎭⎪⎫π6-xC .22sin ⎝ ⎛⎭⎪⎫π3-x D .22cos ⎝ ⎛⎭⎪⎫π3+x D [2cos x -6sin x =22⎝ ⎛⎭⎪⎫12cos x -32sin x=22⎝ ⎛⎭⎪⎫cos π3cos x -sin π3sin x=22cos ⎝ ⎛⎭⎪⎫π3+x .] 3.cos βcos(α-β)-sin βsin(α-β)=________.cos α [cos βcos(α-β)-sin βsin(α-β)=cos[β+(α-β)]=cos α.] 4.已知α,β均为锐角,sin α=55,cos β=1010,求α-β. [解] ∵α,β均为锐角,sin α=55,cos β=1010, ∴sin β=31010,cos α=255.∵sin α<sin β,∴α<β,∴-π2<α-β<0,∴sin(α-β)=sin αcos β-cos αsin β =55×1010-255×31010=-22, ∴α-β=-π4.。
第五章一元函数的导数及其应用(公式、定理、结论图表)一.导数定义:()f x 在点0x 处的导数记作xx f x x f x f x x y x ∆-∆+='=='→∆)()(lim)(|00000二.导数的几何意义函数()f x 在0x 处导数的几何意义,曲线()y f x =在点()()00,P x f x 处切线的斜率是()0k f x '=。
于是相应的切线方程是:()()000y y f x x x '-=-。
注意两种情况:1.曲线()y f x =在点()()00,P x f x 处切线:性质:()0k f x '=切线。
相应的切线方程是:()()000y y f x x x '-=-2.曲线()y f x =过点()00,P x y 处切线:先设切点,切点为(,)Q a b ,则斜率k='()f a ,切点(,)Q a b 在曲线()y f x =上,切点(,)Q a b 在切线()()00y y f a x x '-=-上,切点(,)Q a b 坐标代入方程得关于a,b 的方程组,解方程组来确定切点,最后求斜率k='()f a ,确定切线方程。
三.常见函数的导数公式:①'0C =;②'1()n n x nx -=;③'(sin )cos x x =;④'(cos )sin x x =-;⑤'()ln x x a a a =;⑥x x e e =')(;⑦'1(log )ln a x x a =;⑧xx 1)(ln '=。
四.导数的四则运算和复合函数的求导法则:(1)[()()]()()f x g x f x g x '''±=±(2))()()()(])()(['+'='x g x f x g x f x g x f (3)2)()()()()()()(x g x g x f x g x f x g x f '-'='⎪⎪⎭⎫ ⎝⎛(4)'⋅'='x u u f x u f ))((五.导数的应用:1.利用导数判断函数单调性:设函数()y f x =在某个区间内可导,①'()0f x >⇒()f x 该区间内为增函数;②'()0f x <⇒()f x 该区间内为减函数;注意:当'()f x 在某个区间内个别点处为零,在其余点处为正(或负)时,()f x 在这个区间上仍是递增(或递减)的。