动态规划算法作业.pdf
- 格式:pdf
- 大小:1.12 MB
- 文档页数:15

第三章:动态规划3.1 动态规划的基本概念一、动态决策问题:决策过程具有阶段性和时序性(与时间有关)的决策问题。
即决策过程可划分为明显的阶段。
二、什么叫动态规划(D.P.–Dynamic Program):多阶段决策问题最优化的一种方法。
广泛应用于工业技术、生产管理、企业管理、经济、军事等领域。
三、动态规划(D.P.)的起源:1951年,(美)数学家R.Bellman等提出最优化原理,从而建立动态规划,名著《动态规划》于1957年出版。
四、动态决策问题分类:1、按数据给出的形式分为:•离散型动态决策问题。
•连续型动态决策问题。
2、按决策过程演变的性质分为:•确定型动态决策问题。
•随机型动态决策问题。
五1、阶段(stage)n :作出决策的若干轮次。
n = 1、2、3、4、5。
2、状态(state)S n :每一阶段的出发位置。
构成状态集,记为S nS 1={A},S 2={B 1,B 2,B 3},S 3={C 1,C 2,C 3},S 4={D 1,D 2,D 3},S 5={E 1,E 2}。
阶段的起点。
3、决策(decision)X n :从一个阶段某状态演变到下一个阶段某状态的选择。
构成决策集,记为D n (S n )。
阶段的终点。
D 1(S 1)={X 1(A)}={B 1,B 2,B 3}= S 2,D 2(S 2)={X 2(B 1),X 2(B 2),X 2(B 3)}={C 1,C 2,C 3}=S 3,D 3(S 3)={X 3(C 1),X 3(C 2),X 3(C 3)}={D 1,D 2,D 3}=S 4,D 4(S 4)={X 4(D 1),X 4(D 2),X 4(D 3)}={E 1,E 2}=S 5D 5(S 5)={X 5(E 1),X 5(E 2)}={F;F}={F}。
4、策略(policy):全过程中各个阶段的决策Xn 组成的有序总体{Xn }。
如 A àB2àC1àD1àE2àF5、子策略(sub-policy):剩下的n个阶段构成n子过程,相应的决策系列叫n子策略。





Floyd算法是一种用来寻找图中所有节点对之间最短路径的算法,它的核心思想是动态规划。
Floyd算法的基本原理是:假设图中有n个节点,将所有节点对之间的最短路径长度初始化为它们之间的直接连线长度,然后逐步更新这些距离,直到得到所有节点对之间的最短路径。
在本文中,我们将通过四个例题a1、a2、a3、a4来讲解Floyd算法的具体应用,以帮助读者更好地理解和掌握这一算法。
1. 例题a1【题目】有一个带权有向图,节点数为n,边数为m,求图中任意两点之间的最短路径长度。
【输入】第一行为两个整数n和m,分别表示节点数和边数。
接下来m行,每行包含三个整数a、b、c,表示图中存在一条从节点a到节点b的有向边,边的权值为c。
【输出】输出一个n×n的矩阵,其中第i行第j列的元素表示节点i到节点j的最短路径长度。
如果两点之间不存在路径,则输出一个特定的值(例如9999)。
【样例】输入:5 71 2 21 3 32 3 22 4 53 4 13 5 64 5 3输出:0 2 3 7 99999 0 2 5 89999 9999 0 3 69999 9999 9999 0 39999 9999 9999 9999 0【分析】根据给定的图和节点数,首先初始化一个n×n的矩阵,然后将直接连线的路径长度填入矩阵中。
接下来,利用Floyd算法逐步更新矩阵中的最短路径长度,直到得到所有节点对之间的最短路径长度。
2. 例题a2【题目】有一个带权有向图,节点数为n,边数为m,求图中是否存在负权环。
【输入】第一行为两个整数n和m,分别表示节点数和边数。
接下来m行,每行包含三个整数a、b、c,表示图中存在一条从节点a到节点b的有向边,边的权值为c。
【输出】若存在负权环,则输出"存在负权环",否则输出"不存在负权环"。
【样例】输入:3 31 2 -12 3 -23 1 -3输出:存在负权环【分析】我们可以利用Floyd算法求出图中任意两点之间的最短路径长度,然后再验证是否存在负权环。

动态规划习题Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】动态规划专题分类视图数轴动规题:题1.2001年普及组第4题--装箱问题【问题描述】有一个箱子容量为V(正整数,0≤V≤20000),同时有n个物品(0<n≤30),每个物品有一个体积(正整数)。
要求从n个物品中,任取若干个装入箱内,使箱子的剩余空间为最小。
【输入格式】输入文件box.in有若干行。
第一行:一个整数,表示箱子容量V;第二行:一个整数,表示物品个数n;接下来n行,分别表示这n个物品的各自体积。
【输出格式】输出文件box.out只有一行数据,该行只有一个数,表示最小的箱子剩余空间。
【输入样例】2468312797【输出样例】题2.1996年提高组第4题--砝码秤重__数据加强版【问题描述】设有n种砝码,第k种砝码有Ck 个,每个重量均为Wk,求:用这些砝码能秤出的不同重量的个数,但不包括一个砝码也不用的情况。
【输入格式】输入文件weight.in的第一行只有一个数n,表示不同的砝码的种类数.第2行至第n+1行,每行有两个整数.第k+1行的两个数分别表示第k种砝码的个数和重量.【输出格式】输出文件weight.out中只有一行数据:Total=N。
表示用这些砝码能秤出的不同重量数。
【输入样例】22223【输出样例】Total=8【样例说明】重量2,3,4,5,6,7,8,10都能秤得【数据限制】对于100%的数据,砝码的种类n满足:1≤n≤100;对于30%的数据,砝码的总数量C满足:1≤C≤20;对于100%的数据,砝码的总数量C满足:1≤C≤100;对于所有的数据,砝码的总重量W满足:1≤W≤400000;题3.石子归并-szgb.pas【问题描述】有一堆石头质量分别为W1,W2,…,Wn.(Wi≤10000),将石头合并为两堆,使两堆质量的差最小。
【输入】输入文件szgb.in的第一行只有一个整数n(1≤n≤50),表示有n堆石子。

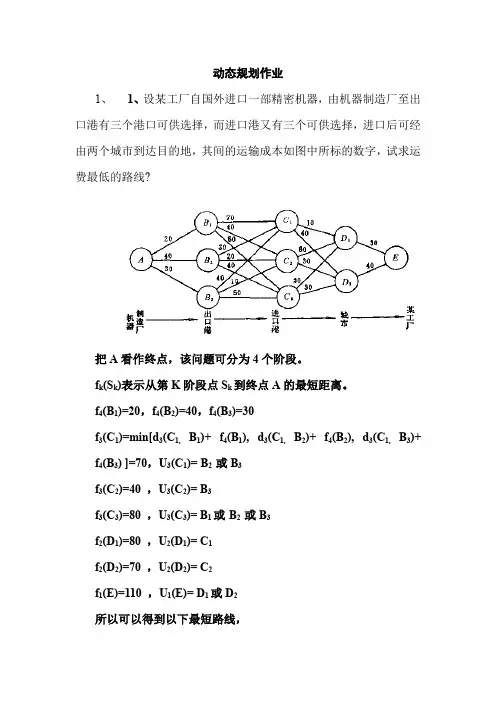
动态规划作业1、1、设某工厂自国外进口一部精密机器,由机器制造厂至出口港有三个港口可供选择,而进口港又有三个可供选择,进口后可经由两个城市到达目的地,其间的运输成本如图中所标的数字,试求运费最低的路线?把A看作终点,该问题可分为4个阶段。
f k(S k)表示从第K阶段点S k到终点A的最短距离。
f4(B1)=20,f4(B2)=40,f4(B3)=30f3(C1)=min[d3(C1,B1)+ f4(B1), d3(C1,B2)+ f4(B2), d3(C1,B3)+ f4(B3) ]=70,U3(C1)= B2 或B3f3(C2)=40 ,U3(C2)= B3f3(C3)=80 ,U3(C3)= B1或B2 或B3f2(D1)=80 ,U2(D1)= C1f2(D2)=70 ,U2(D2)= C2f1(E)=110 ,U1(E)= D1或D2所以可以得到以下最短路线,E→D1→C1→B2 / B3→AE→D2→C2→B3→A2、习题4-2解:1)将问题按地区分为三个阶段,三个地区的编号分别为1、2、3;2)设Sk表示为分配给第k个地区到第n个地区的销售点数,Xk表示为分配给第k个地区的销售点数,S k+1=S k-X kPk(Xk)表示为Xk个销售点分到第k个地区所得的利润值fk(Sk)表示为Sk个销售点分配给第k个地区到第n个地区的最大利润值3)递推关系式:fk(Sk)=max[ Pk(Xk)+ f k+1(S k-X k) ] k=3,2,1f4(S4)=04)从最后一个阶段开始向前逆推计算第三阶段:设将S3个销售点(S3=0,1,2,3,4)全部分配给第三个地区时,最大利润值为:f3(S3)=max[P3(X3)] 其中X3=S3=0,1,2,3,4表1第二阶段:设将S2个销售点(S2=0,1,2,3,4)分配给乙丙两个地区时,对每一个S2值,都有一种最优分配方案,使得最大盈利值为:f2(S2)=max[ P2(X2)+ f3(S2-X2) ]其中,X2=0,1,2,3,4表2第一阶段:设将S1个销售点(S1=4)分配给三个地区时,则最大利润值为:f1(S1)=max[ P1(X1)+ f2(4-X1) ]其中,X1=0,1,2,3,4表3然后按计算表格的顺序反推,可知最优分配方案有两个:最大总利润为531)由X1*=2,X2*=1,X3*=1。
1
第五章 动态规划作业题及答案
1.用动态规划法求解求最短路径
从起点A 到终点E 之间各点的距离如图所示。
求A 到E 的最短路径。
B A
C B
D B C D E
C 21
23
12
31
2
5
11214
10610
41312113
96
5810
5
2
2.用动态规划法求解资源分配问题
有资金4万元,投资A 、B 、C 三个项目,每个项目的投资效益与投入该项目的资金有关。
三个项目A 、B 、C 的投资效益(万吨)和投入资金(万元)的关系见下表:
用动态规划法求解对三个项目的最优投资分配,使总投资效益最大。
3.用动态规划法求解生产库存问题
一个工厂生产某种产品,1~7月份生产成本和产品需求量的变化情况如下表:
为了调节生产生产和需求,工厂设有一个产品仓库,库容量H=9。
已知期初库存量为2,要求期末(七月低)库存量为0。
每个月生产的产品在月末入库,月初根据当月需求发货。
求七个月的生产量,能满足各月的需求,并使生产成本最低。
4.用动态规划法求解背包问题
第i 种每件价值c 1=65,c 2=85,c 3=40元; 第i 种物品每件重量为:w 1=2,w 2=3,w 3=1公斤;现有一只可装载重量为5公斤的背包,求各种物品应各取多少件放入背包,使背包中物品的价值最高。

算法设计与分析——流⽔作业调度(动态规划)⼀、问题描述N个作业{1,2,………,n}要在由两台机器M1和M2组成的流⽔线上完成加⼯。
每个作业加⼯的顺序都是先在M1上加⼯,然后在M2上加⼯。
M1和M2加⼯作业i所需的时间分别为ai和bi,1≤i≤n。
流⽔作业⾼度问题要求确定这n个作业的最优加⼯顺序,使得从第⼀个作业在机器M1上开始加⼯,到最后⼀个作业在机器M2上加⼯完成所需的时间最少。
⼆、算法思路直观上,⼀个最优调度应使机器M1没有空闲时间,且机器M2的空闲时间最少。
在⼀般情况下,机器M2上会有机器空闲和作业积压2种情况。
最优调度应该是:1. 使M1上的加⼯是⽆间断的。
即M1上的加⼯时间是所有ai之和,但M2上不⼀定是bi之和。
2. 使作业在两台机器上的加⼯次序是完全相同的。
则得结论:仅需考虑在两台机上加⼯次序完全相同的调度。
设全部作业的集合为N={1,2,…,n}。
S是N的作业⼦集。
在⼀般情况下,机器M1开始加⼯S中作业时,机器M2还在加⼯其他作业,要等时间t后才可利⽤。
将这种情况下完成S中作业所需的最短时间记为T(S,t)。
流⽔作业调度问题的最优值为T(N,0)。
这个T(S,t)该如何理解?举个例⼦就好搞了(⽤ipad pencil写的...没贴类纸膜,太滑,凑合看吧)1、最优⼦结构T(N,0)=min{ai + T(N-{i}, bi)}, i∈N。
ai:选⼀个作业i先加⼯,在M1的加⼯时间。
T(N-{i},bi}:剩下的作业要等bi时间后才能在M2上加⼯。
注意这⾥函数的定义,因为⼀开始⼯作i是随机取的,M1加⼯完了ai之后,要开始加⼯bi了,这⾥M1是空闲的可以开始加⼯剩下的N-i个作业了,但此时M2开始加⼯bi,所以要等bi时间之后才能重新利⽤,对应到上⾯函数T(s,t)的定义的话,这⾥就应该表⽰成T(N-{i},bi), 所以最优解可表⽰为T(N,0)=min{ai + T(N-{i}, bi)}, i∈N,即我们要枚举所有的⼯作i,使这个式⼦取到最⼩值。
作业就是写代码测测的题目作业1 2004.t3合唱队形作业2 2008.t1能量项链作业3 2007.t3矩阵取数作业4奶牛食物农民John购买了一处肥沃的矩形牧场,分成M*N(1<=M<=12;1<=N<=12)个格子。
他想在那里的一些格子中种植美味的玉米。
遗憾的是,有些格子区域的土地是贫瘠的,不能耕种。
精明的FJ知道奶牛们进食时不喜欢和别的牛相邻,所以一旦在一个格子中种植玉米,那么他就不会在相邻的格子中种植,即没有两个被选中的格子拥有公共边。
他还没有最终确定哪些格子要选择种植玉米。
作为一个思想开明的人,农民John希望考虑所有可行的选择格子种植方案。
由于太开明,他还考虑一个格子都不选择的种植方案!请帮助农民John确定种植方案总数。
【输入格式】第1行:两个用空格分隔的整数M和N第2..M+1行:第i+1行描述牧场第i行每个格子的情况,N个用空格分隔的整数,表示这个格子是否可以种植(1表示肥沃的、适合种植,0表示贫瘠的、不可种植)【输出格式】一个整数:FJ可选择的方案总数除以100,000,000的余数。
【输入样例】2 31 1 10 1 0【输出样例】9【输出解释】给可以种植玉米的格子编号:1 2 30 4 0只种一个格子的方案有四种(1,2,3或4),种植两个格子的方案有三种(13,14或34),种植三个格子的方案有一种(134),还有一种什么格子都不种。
4+3+1+1=9。
作业5 2010.t2乌龟棋作业6 2011.d1.t2选择客栈作业7 2013.d2.t2花匠(有其它方法)作业8 2015.d2.t1跳石头(可以二分答案)作业9 2015.d2.t2子串作业10 2006.t2预算方案作业11 2014.d1.t3飞扬的小鸟作业12 WaveDescription波在不同的介质中的传播速度是不一样的。
真空中波速都是3*108m/s,而在液体介质中的波速会比真空中的波速小,并且在不同的液体介质中波速不一样。
动态规划算法题(5题)1、题⽬描述(⽹易)有 n 个学⽣站成⼀排,每个学⽣有⼀个能⼒值,⽜⽜想从这 n 个学⽣中按照顺序选取 k 名学⽣,要求相邻两个学⽣的位置编号的差不超过d,使得这 k 个学⽣的能⼒值的乘积最⼤,你能返回最⼤的乘积吗?输⼊描述:每个输⼊包含 1 个测试⽤例。
每个测试数据的第⼀⾏包含⼀个整数 n (1 <= n <= 50),表⽰学⽣的个数,接下来的⼀⾏,包含 n 个整数,按顺序表⽰每个学⽣的能⼒值 ai(-50 <= ai <= 50)。
接下来的⼀⾏包含两个整数,k 和 d (1 <= k <= 10, 1 <= d <= 50)。
输出描述:输出⼀⾏表⽰最⼤的乘积。
试题分析:本题要使⽤动态规划来解,动态规划的特点:1.求解的是最优化问题;2.可以分解为最优⼦结构本题可以先求解在第i个学⽣的位置下,j(j<K)个学⽣的能⼒值的最⼤值,得到所有学⽣位置下j个学⽣的能⼒值的最⼤值;在j个学⽣的情况下,得到j+1个学⽣的最⼤值,样例输出: 10 8 7 2 -7 9 5 4 10 -7 1 3 3输出: 630如上,第⼀步先计算k=2的情况:7:在d=3的情况下,最⼤最⼩值都为562:在d=3的情况下,最⼤值为16,最⼩值为14-7:在d=3的情况下,最⼤值为-14,最⼩值为-56......得到第⼀趟的结果k=3的情况下(这⾥以第⼀趟的结果为基础,只有这样就不需要考虑第⼀趟中d=3的限制):2:在d=3的情况下,最⼤最⼩值都为112(56*2)-7:在d=3的情况下,最⼤值为-98(14*-7)最⼩值为-392(56*-7)9:在d=3的情况下,最⼤值为504(56*9)最⼩值为-504(-56*9)......得到第⼆趟的结果返回最⼤值就是最后的结果#-*- coding:utf-8 -*-n=input()array=[int(i) for i in raw_input().split()]k,d=[int(i) for i in raw_input().split()]# n=36array_max=array_min=array#轮询k-1趟即可for i in range(0,k-1):_max=[-float('inf')]*n#将最⼤值的数组赋值⽆穷⼩_min=[float('inf')]*n#将最⼩值的数组赋值⽆穷⼤for j in range(i+1,n):if j<=d+i:#下⾯对应的min、max都是考虑到array[j]为负值的情况下temp_max = max(max(ii*array[j] for ii in array_max[i:j]),max(ii*array[j] for ii in array_min[i:j]))temp_min = min(min(ii*array[j] for ii in array_max[i:j]),min(ii*array[j] for ii in array_min[i:j]))else:temp_max = max(max(ii*array[j] for ii in array_max[j-d:j]),max(ii*array[j] for ii in array_min[j-d:j]))temp_min = min(min(ii*array[j] for ii in array_max[j-d:j]),min(ii*array[j] for ii in array_min[j-d:j]))_max[j]=temp_max_min[j]=temp_minarray_max=_maxarray_min=_minprint array_maxprint array_minprint max(array_max)2、题⽬描述(腾讯):腾讯⼤厦有39层,你⼿⾥有两颗⼀抹⼀眼的玻璃珠。
1.最大子段和问题:给定整数序列 n a a a ,,,21 ,求该序列形如∑=jik k a 的子段和的最大值: ⎭⎬⎫⎩⎨⎧∑=≤≤≤ji k k n j i a 1max ,0max1) 已知一个简单算法如下:int Maxsum(int n,int a,int& best i,int& bestj){ int sum = 0;for (int i=1;i<=n;i++){ int suma = 0;for (int j=i;j<=n;j++){ suma + = a[j]; if (suma > sum){ sum = suma; besti = i; bestj = j; } }}return sum;}试分析该算法的时间复杂性。
2) 试用分治算法解最大子段和问题,并分析算法的时间复杂性。
3) 试说明最大子段和问题具有最优子结构性质,并设计一个动态规划算法解最大子段和问题。
分析算法的时间复杂度。
(提示:令1()m ax,1,2,,jki j nk ib j aj n≤≤≤===∑ )解:1)分析按照第一章,列出步数统计表,计算可得)(2n O2)分治算法:将所给的序列a[1:n]分为两段a [1:n/2]、a[n/2+1:n],分别求出这两段的最大子段和,则a[1:n]的最大子段和有三种可能: ①a[1:n]的最大子段和与a[1:n/2]的最大子段和相同; ②a[1:n]的最大子段和与a[n/2+1:n]的最大子段和相同; ③a[1:n]的最大子段和为两部分的字段和组成,即j n jil n i ja a a a a+++++=+⎥⎦⎥⎢⎣⎢=⎥⎦⎥⎢⎣⎢∑ 122;intMaxSubSum ( int *a, int left , int right){int sum =0;if( left==right)sum = a[left] > 0? a[ left]:0 ;else{int center = ( left + right) /2;int leftsum =MaxSubSum ( a, left , center) ;int rightsum =MaxSubSum ( a, center +1, right) ;int s_1 =0;int left_sum =0;for ( int i = center ; i >= left; i--){left_sum + = a [ i ];if( left_sum > s1)s1 = left_sum;}int s2 =0;int right_sum =0;for ( int i = center +1; i <= right ; i++){right_sum + = a[ i];if( right_sum > s2)s2 = right_sum;}sum = s1 + s2;if ( sum < leftsum)sum = leftsum;if ( sum < rightsum)sum = rightsum;}return sum;}int MaxSum2 (int n){int a;returnMaxSubSum ( a, 1, n) ;} 该算法所需的计算时间T(n)满足典型的分治算法递归分式T(n)=2T(n/2)+O(n),分治算法的时间复杂度为O(nlogn)3)设}{m a x )(1∑=≤≤=jik k ji a j b ,则最大子段和为).(max maxmax maxmax 11111j b aanj jik kji n j jik knj n i ≤≤=≤≤≤≤=≤≤≤≤==∑∑},,,,max{)(11211j j j j j j j a a a a a a a a a j b +++++=---最大子段和实际就是)}(,),2(),1(max{n b b b .要说明最大子段和具有最优子结构性质,只要找到其前后步骤的迭代关系即可。
1 n←length(T)2 create array x[1:L]3 for j←1 to L4 d o x[j]←j/T[1]5 for i←2 to n6 do for j←L to 17 do for k←1 to j/T[i]8 do if x[j-k*x]+k<x[j]9 then x[j]←x[j-k*x]+k10 return x时间复杂度分析:算法1~2行时间复杂度为O(1),3~4行时间复杂度为O(L),5~9行时间复杂度为O(nL2),10行时间复杂度为O(1)。
故算法总的时间复杂度为O(nL2)。
(3)设y[1:n]存储当找钱数为j的最优解时T[1:n]硬币分别找的个数。
选择面值最大的T[i],1≤i≤n,使C[n,j]=C[n,j-T[i]]+1,则子问题找钱数为j-T[i]的最优解y’[1:n]中,y’[i]+1后即为原问题的最优解y[1:n]。
故问题的最优解可以通过子问题的最优解来达到,该问题具有贪心选择性。
(假设T[1:n]的面值是递增的,并且C[n,L]是与排序后的T对应的结果)Input:T[1:n], C[1:L], mOutput:每个硬币对应的数目y[1:n]GET-CHANGE-NUMBER(T,C,m)1 n←length(T),w←m2 create array y[1:n]3 for i←1 to n4 do y[i]←05 while w>06 do for i←n to 17 do if C[w]=C[w-T[i]]+18 then y[i]←y[i]+19 w←w-T[i]10 break11 return y时间复杂性分析:算法1~2行时间复杂度为O(1),2~3行时间复杂度为O(n),5~10行时间复杂度为O(m×n),11行时间复杂度为O(1)。
故算法总的时间复杂度为O(m×n)。
2.设计一个动态规划算法从n个数构成的数列中找出最长单调递增子序列。
答:(1)问题转化:设X[1:n]为n个数构成的序列,Y[1:n]为将X[1:n]中的数进行递增排序的结果。
那么,原问题可以转化为求X和Y的最长公共子序列。
设X中的最长单调递增子序列为x i, x j, …, x k, x m,那么在排序后的Y中,该子序列仍以这一顺序存在于Y中,显然该序列为X和Y的公共子序列。
假设其不是X和Y的最长公共子序列,设其最长公共子序列为x i, x j, …, x p, …, x k, x m。
由于Y为递增序列,因此有x i<x j<…<x p<…<x k<x m。
又因为x i, x j, …, x p, …, x k, x m是X的子序列,那么在X序列中,有一个更长的单调递增子序列x i, x j, …, x p, …, x k, x m。
产生了矛盾,因此X的最长单调递增子序列即为X和Y的最长公共子序列。
(2)优化子结构X和Y的LCS=(z1,z2,…,z k)的优化解结构为LCS XY=LCS X+<x m=y n> if x m=y nm−1Y n−1if x m≠y n,z k≠x mLCS XY=LCS Xm−1Yif x m≠y n,z k≠y mLCS XY=LCS XYn−1(3)递推方程C[i,j]=X i和Y j的LCS的长度C[i,j]=0 if i=0或j=0C[i,j]=C[i−1,j−1]+1 if i,j>0且x i=y jC[i,j]=max (C[i,j−1],C[i−1,j]) if i,j>0且x i=y j (4)算法伪代码Input:数列X[1:n]Output:X的最长单调递增子序列LIS(X)1 n←length(X)2 create array Y[1:n] ,C[n,n] and B[n,n]3 Y←sort(X)4 for i←1 to n5 do C[i,0]←0,C[0,j]←06 for i←1 to n7 do for j←1 to n8 if X[i]=Y[j]9 then C[i,j]←C[i-1,j-1]+1;B[i,j]←“↖”10 else if C[i-1,j]≥C[i,j-1]11 then C[i,j]←C[i-1,j]; B[i,j]←“↑”12 else C[i,j]←C[i,j-1]; B[i,j]←“←”13 return B and CPRINT-LIS(B,X,i,j)1 if i←0 or j←02 then return3 if B[i,j]= “↖”4 then PRINT-LIS(B,X,i-1,j-1);print X[i]5 else if B[i,j]= “↑”6 then PRINT-LIS(B,X,i-1,j);7 else PRINT-LIS(B,X,i,j-1);时间复杂度分析:计算代价算法LIS(X)中,1~2行时间复杂度为O(1),3行为排序算法,时间复杂度最低为O(nlogn),4~5行时间复杂度为O(n),6~12行时间复杂度为O(n2),13行时间复杂度为O(1);构造算法PRINT-LIS(B,X,i,j)中,时间复杂度为O(2n)。
故算法总的时间复杂度为O(n 2)。
3.给定一个n×n 的矩阵A ,矩阵中的元素只取0或者1。
设计一个动态规划算法,求解得到A 中元素全是1的子方阵使其阶数达到最大值。
答:(1)优化子结构:设n 阶矩阵表示为A[1:n,1:n],B[i,j]为A 中前i 行,前j 列中1的个数。
则⎩⎨⎧==++=1A[i][j] if 10A[i][j] if 0B -B B B 1-j 1,-i 1-j i,j 1,-i j i, 如果B i,j -B i-k,j - B i,j-k +B i-k,j-k =k 2,那么在该位置存在一个k 阶矩阵。
(2)递推方程:设C[i,j]表示A 中前i 行前j 列中元素全为1的子方阵的最大阶数。
则递推方程为:C [i,j ]=max {C [i −1,j ],C [i,j −1],max k{k ≥max (C [i −1,j ],C [i,j −1])| B [i,j ]−B [i −k,j ]−B [i,j −k ]+B [i −k ][j −k ]=k ×k}}(3)算法伪代码只要知道了C n,n 的值,就知道了最优解的阶数,为了知道这个最优解的具体信息,我们还需一个结构S ,S i,j 是C i,j 对应的方阵的右下角元素在A 中对应的位置。
因此,S n,n 就是最优解方阵右下角元素的位置,C n,n 是最优解的阶数。
GET-MAX-MATRIX(A,n)1 create arrays B[0:n][0:n],C[0:n][0:n],S[1:n][1:n]2 for i←0 to n3 do B[i][0]←0; B[0][i]←0;C[i][0]← 0; C[0][i]←0;4 for i←0 to n5 do for j←0 to n6 do if A[i][j]=17 then B[i][j]←18 else B[i][j]←09 B[i][j]←B[i][j]+B[i-1][j]+B[i][j-1]+B[i-1][j-1]10if C[i-1][j]>C[i][j-1]11 then C[i][j]←C[i-1][j]12 S[i][j]←C[i-1][j]13 else C[i][j]←C[i][j-1]14 S[i][j]←C[i][j-1]15 for k←C[i][j]+1 to i16 do if i-k+1<1 or j-k+1<017 then break18 if B[i][j]-B[i-k+1][j]-B[i][j-k]+B[i-k][j-k]=k×k19 then C[i][j]←k20 S[i][j] (i,j)21 else break22 return S and C算法结束后,S[n][n]中有序实数对(i,j)为A 中最大全1矩阵右下角元素的坐标。
该矩阵为A[i-C[n][n]:i][j-C[n][n]:j]。
时间复杂度分析:算法第1行时间复杂度为O(1),2~3行时间复杂度为O(n),4~22行时间复杂度为O(n 3),23行时间复杂度为O(1)。
故算法总的时间复杂度为O(n 3)。
4.集合划分问题描述如下:输入:正整数集合 S={a 1,a 2,a 3,…, a n };输出:是否存在A ⊆ S 使得∑a i =∑a i a i ∈S−A a i ∈A 。
试设计一个动态规划算法,求解集合划分问题。
答:(1)问题转化:若集合划分A 使得∑a i =∑a i a i ∈S−A a i ∈A ,则有∑a i =∑a i =12∑a i a i ∈S a i ∈S−A a i ∈A 。
那么,该问题可转化为一个0-1背包问题。
对于输入的正整数集合S={a 1,a 2,a 3,…, a n }。
设X=(x 1, x 2, …, x n ),x i ∈{0, 1}, 满足∑x i a i n i=1≤12∑a i a i ∈S ,且∑x i a i n i=1最大。
若此时∑x i a i n i=1=12∑a i a i ∈S , 则存在这样的集合划分A ,输出划分结果;否则不存在这样的集合A 。
(2)优化子结构:如果(y 1, y 2,…, y n )是0-1背包问题的有化解,则(y 2, y 3,…, y n )是如下子问题的优化解:∑x i a i n i=2≤12∑a i a i ∈S −a 1y 1;x i ∈{0, 1},2≤i ≤n 。
(3)递推方程:设背包容量为j ,m(i,j)表示背包容量为j ,可选物品为a i ,a i+1,…, a n 时,问题的最优解的代价。
因此递归方程为:m(i,j)=m(i+1,j) 0≤j<a im(i,j)=max(m(i+1,j),m(i+1,j−a i)+a i) j≥a im(n,j)=0 0≤j<a nm(n,j)=a n j≥a n(4)算法伪代码:Input:正整数集合S={a1,a2,a3,…, a n}Output:若存在A ⊆S使得∑a i=∑a ia i∈A, 则输出X; 否则输a i∈S−A出不存在。
SET-PARTITION(S)1 n←length(S),sum←02 for i←1 to n3 do sum←sum+S[i]4 half-sum←sum/25 create array m[1:n,0: half-sum] and X[1:n]6 for j←0 to min(S[n]-1, half-sum)7 do m[n,j]←08 for j←S[n] to half-sum9 do m[n,j]←S[n]10 for i←n-1 to 211 do for j←0 to min(S[i]-1, half-sum)12 do m[i,j]←m[i+1,j]13 for j←S[i] to half-sum14 do m[i,j]←max{m[i+1,j],m[i+1,j-S[i]]+S[i]}15 if half-sum <S[1]16 then m[1, half-sum]=m[2, half-sum]17 else m[1, half-sum]=max{m[2, half-sum],m[2, half-sum -S[1]]+S[1]}18 if m[1, sum/2] < sum/219 then return “不存在”20 w←half-sum21for i←1 to n-122 do if m[i,w]=m[i+1, w]23 then X[1]=024 else X[1]=125 w←w-S[i]26 if w≥S[n]27 then X[n]=028 else X[n]=129 return X时间复杂度分析:第1行时间复杂度为O(1),2~3行时间复杂度为O(n),4~5行时间复杂度为O(1),6~9行时间复杂度为O(n),10~14行时间复杂度为O(n×half-sum),15~20行时间复杂度为O(1),21~26行时间复杂度为O(n),27~29行时间复杂度为O(1)。