重庆开县2015届九年级上学期期末考试

开县2014-2015学年度（上）期末质量检测九年级历史试题一、单项选择题：本大题共15小题，每小题1分，共15分。

在备选答案中只有一项是符合题目要1.关于人类文明产生的自然地理环境，你能从下面两幅地图中得到的信息是亚非文明发源地欧洲文明发源地A.东方文明产生较早，西方文明出现相对较晚B.东方文明产生于大河流域，西方文明发源于海洋C.东方文明以农耕为主，西方文明工商业发达D.东方人传统保守，西方人冒险进取2.作为文明古国之一，印度文明有其独特的魅力。

下列与印度文明有关的有①佛教②阿拉伯数字③种姓制度④《汉谟拉比法典》A.①②③B.②③④C.①②D.①③3.大化改新是大和民族发展史上的一次重要事件，下列历史知识概述准确的是①苏我氏父子专权，统治出现危机②中大兄皇子依靠西乡隆盛等人，效仿中国隋唐制度进行改革③实行中央集权④使日本由奴隶社会过渡到封建社会A.①②③B.①②④C.①③④D.②③④4.《剑桥古代史》对古代雅典有这样的描述：“（雅典公民）不仅可以享受到阿提卡的橄榄油和葡萄酒，而且可以食用黑海的谷物和干鱼……穿波斯的拖鞋，睡爱尔兰的床……”从材料中可以看出雅典A.物产丰富，人民富足B.工商业非常发达C.民主政治发展到顶峰D.地中海霸主地位确立5.课堂上同学们互相交流自学的情况，下列同学们的发言有误的一项是A.小王：埃及人发明了象形文字，其书写材料是纸草B.小张：欧洲第一部优秀的文学作品是《荷马史诗》C.小李：通过帮国王鉴别王冠的真假，阿基米德发现了浮力定律D. 小赵：巴黎圣母院是阿拉伯建筑的代表6.某初三同学在学习了世界近代史第一学习主题后。

整理了以下笔记，其中有误的一项是A.欧美国家的巨变是指欧美大国推翻封建专制统治，建立新的资本主义制度B.巴黎人民攻占巴士底狱，揭开了法国大革命的序幕C.设计了美国政府体制方面的文献是《1787年宪法》D.从三角贸易，我们看出了资本原始积累的野蛮性和残酷性7.同学们对拿破仑和华盛顿的主要活动进行总结，发现他们的共同点①他们进行的战争都具有进步和侵略性质②他们都注重法制建设③他们都促进了本国资本主义的发展④他们都是著名的资产阶级革命家和总统A.①②B.①③C.②③D.①④8．“在占据莱茵河和许多小邦国后，拿破仑赶跑了那里的封建王公贵族和主教，取消了各种徭役和教会什一税，清扫了德国的奥吉亚斯的牛圈，修筑了文明的交通大道……”材料反映出拿破仑对外战争A.解除了法国的外来威胁B.冲击了欧洲的封建制度C.具有民族压迫的性质D.促进了西欧城市的兴起9.下列历史事件按照出现时间先后排列，顺序正确的是A．《权利法案》发表——滑铁卢之战——列克星顿枪声——《解放奴隶宣言》发表B．《权利法案》发表——列克星顿枪声——滑铁卢之战——《解放奴隶宣言》发表C.列克星顿枪声——《权利法案》发表——《解放奴隶宣言》发表——发表滑铁卢之战D.列克星顿枪声——《解放奴隶宣言》发表——《权利法案》发表——滑铁卢之战10．运用数据进行分析是历史学习的一种重要方法。

2015-2016学年重庆市开县云枫中学九年级（上）期末物理试卷一、选择题（每小题3分，共24分．在每题给出的四个选项中只有一项是正确的）1．四冲程汽油机的工作过程中，气缸内气体内能增加的冲程是（）A．吸气冲程 B．压缩冲程 C．做功冲程 D．排气冲程2．关于温度、内能和热量，下列说法正确的是（）A．物体温度越低，分子运动越剧烈B．物体温度越高，含有的热量越多C．物体的温度为0℃时，其内能为零D．海波熔化时温度不变，其内能增加3．下列现象中，用做功的方法改变物体内能的是（）A．酒精涂在手上觉得凉B．冬天晒太阳，人感到暖和C．锯木头时，锯条会发烫 D．烧红的铁块温度逐渐降低4．下列物体中，通常情况下属于导体的是（）A．钢筋 B．空气 C．玻璃棒D．塑料尺5．如果不考虑温度的影响，导体的电阻的大小与下列哪个因素无关（）A．导体的材料B．导体的长度C．导体的横截面积D．导体两端的电压6．小华把一支签字笔的一端在头发上摩擦几下，被摩擦的一端将带上负电，然后用被摩擦的一端靠近悬挂着的气球，结果出现了如图所示的情景，由此可判断（）A．气球原来一定带正电B．气球原来一定带负电C．气球原来可能带负电，也可能不带电D．气球原来一定不带电7．如图所示的电路有严重错误，为了使该电路恢复正常，应该去掉其中一根导线，下列判断正确的是（）A．去掉导线①B．去掉导线②C．去掉导线③D．去掉导线④8．某导体中的电流与它两端电压的关系如图所示，下列分析正确的是（）A．当导体两端的电压为0时，电阻为0B．该导体的电阻随电压的增大而减小C．把该导体接到电压为4V的电源上，电流为0.8AD．当导体两端的电压为2V时，电流为0.6A二．填空题（每空1分，共14分）9．在内燃机的“吸气”、“压缩”、“做功”、“排气”四个冲程中，将内能转化为机械能的是冲程；常用水来给内燃机降温，是因为水的比较大．10．炒菜是生活中常见的热现象，炒菜时利用的方法增加了菜的内能，由于分子的现象我们在整个厨房都会闻到菜的香味．11．气体非常容易压缩说明分子间存在，固体很难被压缩说明分子间存在相互作用的．12．某太阳能热水器的水箱中装有体积为0.2m3的水，在阳光的照射下，水的温度从20℃升高到70℃．则热水器中水的质量是kg，水吸收了J的热量．[已知水的密度为1.0×103kg/m3，水的比热容为4.2×103 J/（kg•℃）]．13．小明家卫生间安装了集取暖、照明和换气于一身的“浴霸”，“浴霸”中的换气扇、照明灯和取暖灯的电路连接如图所示．当换气扇和照明灯同时工作时，换气扇两端的电压（选填“大于”、“等于”或“小于”）照明灯两端的电压，在此基础上接通控制取暖灯的开关让取暖灯也一起工作，通过“浴霸”装置的干路中的总电流将（选填“增大”、“减小”或“不变”）．14．一个滑动变阻器上标有“5Ω 3A”的字样，这个滑动变阻器能够接入电路的最大电阻是Ω，在电路中正常工作时允许通过滑动变阻器的最大电流是A．15．给一个定值电阻两端加上2.4V电压，测得通过的电流为0.4A，则该定值电阻的阻值为Ω，当它两端电压增加到3V时，通过的电流为A．三．实验与探究题（16题4分，17题7分，18题10分，共21分）16．请你把图1所示的实物电路的电路图画在图2的虚线框内，并在电路图上标明电流表的“+”、“﹣”接线柱．17．小华同学所在的学习小组为了探究串联电路的电压特点，他们设计了如图甲所示的电路进行实验（1）同学们按图甲所示的电路图连接实物电路时，开关S应处于状态．电路连接好后，同学们试触开关S时发现电压表的指针向着没有刻度的左侧偏转（如图乙所示），出现这种情况的原因是电压表的．（2）学习小组的同学用电压表的两端分别连接到电路中A与B、B与C、和A与C上，测出A、B间电压U AB=1.5V，另外两次测量的电压表示数如图中丙、丁所示，可读出：U BC= V，U AC= V．根据测量结果，可以初步得出结论：串联电路的总电压．（3）为了排除实验探究的偶然性，验证结论具有普遍性，可以更换不同的或者更换不同的重复上述实验若干次．18．某实验小组探究电流与电压的关系时，所用器材如下：电源1个，电流表、电压表各1只，定值电阻1个，滑动变阻器1只，开关1个，导线若干；设计的电路如图甲所示．实验I/A 0.16 0.24 0.36 0.40 0.44（1）请根据图甲所示电路和表中的实验数据，将图乙所示的实物电路中未连接的导线端①和②连接到合适的接线柱上．将滑动变阻器的滑片P移到（选填“最左端”、“中央”或“最右端”）后才能闭合．（2）闭合开关后，发现电流表的指针并不发生偏转，电压表的指针发生了偏转，可能发生的故障是：．（3）请根据表中数据在图丙的坐标中画出电流随电压变化的图象．（4）分析表中的数据或图象，你能得出的实验结论：．（5）该实验小组还利用此电路探究“通过导体的电流与导体电阻的关系”，依次用8Ω、12Ω和16Ω的电阻替换原来的定值电阻，实验过程中应使电压表读数（选填“变大”、“变小”或“不变”），更换不同阻值的电阻器后，调节滑动变阻器滑片P位置的同时，眼睛紧盯，直到符合要求后，再读取的读数．四．计算题（19题6分、20题7分，21题8分，共21分．解答应写出必要的文字说明、解答步骤和公式，只写出最后答案不能得分）19．焦炭的热值q=3.0×107J/kg，水的比热容为4.2×103J/（kg•℃）．完成下列问题：（1）完全燃烧0.14kg的焦炭能够放出的热量是多少？（2）焦炭放出的热量全部被质量为25kg、初温为20℃的水吸收后，水的温度是多少？20．一个小灯泡正常发光时，两端电压为U0=2.5V，通过的电流为I0=0.3A．（1）求小灯泡正常发光时灯丝的电阻R0；（2）现在只有电压为10V的电源，要给小灯泡串联一个电阻值为R的电阻后接到电源上，灯泡才能正常发光，求R=？21．如图电路中，电源电压保持不变，定值电阻R1=3Ω，R2是滑动变阻器．只闭合S1，电流表读数为I1=2A．完成下列问题：（1）求电源电压U；（2）将S1、S2都闭合，且将滑动变阻器的滑片置于b端，电流表的读数改变了0.5A．求滑动变阻器的最大阻值R0；（3）再将滑片P移至滑动变阻器的中央时，电流表读数是多少？2015-2016学年重庆市开县云枫中学九年级（上）期末物理试卷参考答案与试题解析一、选择题（每小题3分，共24分．在每题给出的四个选项中只有一项是正确的）1．四冲程汽油机的工作过程中，气缸内气体内能增加的冲程是（）A．吸气冲程 B．压缩冲程 C．做功冲程 D．排气冲程【考点】内燃机的四个冲程．【分析】在内燃机的做功冲程中能量转化是内能转化为机械能，压缩冲程中能量转化是机械能转化为内能．【解答】解：四冲程汽油机的工作过程中，在压缩冲程，活塞压缩汽油与空气形成的燃料混合物，活塞对气体做功，将机械能转化为气体的内能，使气缸内气体内能增加．故选B．2．关于温度、内能和热量，下列说法正确的是（）A．物体温度越低，分子运动越剧烈B．物体温度越高，含有的热量越多C．物体的温度为0℃时，其内能为零D．海波熔化时温度不变，其内能增加【考点】温度、热量与内能的关系．【分析】A、分子的热运动与温度有关，温度越高，运动越剧烈．B、热量是一个过程时，不能用具有、含有来修饰；C、一切物体在任何温度下都具有内能；D、晶体熔化时，吸收热量、内能增加，但温度不变．【解答】解：A、分子的热运动与温度有关，物体温度越高，它的分子无规则运动越剧烈，说法错误．B、热量是一个过程量，不能用具有、含有来修饰，说法错误．C、物体在任何温度下都具有内能，所以0℃的物体仍然具有内能．说法错误．D、海波熔化时，吸收热量，但温度不变，内能一定增加，说法正确．故选D．3．下列现象中，用做功的方法改变物体内能的是（）A．酒精涂在手上觉得凉B．冬天晒太阳，人感到暖和C．锯木头时，锯条会发烫 D．烧红的铁块温度逐渐降低【考点】做功改变物体内能；热传递改变物体内能．【分析】逐个分析选择项中提到的物理情景，然后与改变物体内能的方法：做功、热传递对应，从而得到答案．【解答】解：A、酒精涂在手上，酒精蒸发，蒸发吸热，这是利用热传递的方法来减小了手的内能．故A错误．B、晒太阳，是通过热传递的方法，使人的内能增加．故B错误．C、锯木头时，锯与木头摩擦，摩擦生热这是利用做功来改变物体内能的．故C正确．D、铁块的温度降低，是内能从铁块传递到了周围的环境，是通过热传递改变了物体的内能．故D错误．故选C4．下列物体中，通常情况下属于导体的是（）A．钢筋 B．空气 C．玻璃棒D．塑料尺【考点】导体．【分析】容易导电的物体是导体，不容易导电的物体是绝缘体．根据导体和绝缘体的定义即可作出判断．【解答】解：常见的导体包括：人体、大地、各种金属、石墨、酸碱盐的溶液等．题中选项中，只有钢筋是金属，属于导体，空气、玻璃棒、塑料尺都是绝缘体．故选A．5．如果不考虑温度的影响，导体的电阻的大小与下列哪个因素无关（）A．导体的材料B．导体的长度C．导体的横截面积D．导体两端的电压【考点】影响电阻大小的因素．【分析】如果把导体比作一条公路，电阻比作堵车事故：水泥路面比土道畅通，即材料影响电阻；宽敞的路比窄路畅能，即横截面积影响电阻；路越长堵车机会越大，即长度影响电阻．【解答】解：电阻是导体本身的一种性质，电阻大小的影响因素有材料、长度、横截面积、温度，与电压、电流等外界因素无关．根据影响电阻大小的因素来判断，A、B、C都影响电阻，D不影响．故选D．6．小华把一支签字笔的一端在头发上摩擦几下，被摩擦的一端将带上负电，然后用被摩擦的一端靠近悬挂着的气球，结果出现了如图所示的情景，由此可判断（）A．气球原来一定带正电B．气球原来一定带负电C．气球原来可能带负电，也可能不带电D．气球原来一定不带电【考点】物体带电情况的判断；摩擦起电．【分析】吸引有两种情况：异种电荷相互吸引，带电体吸引轻小物体．根据上面的情况进行判断．【解答】解：被摩擦的一端将带上负电，由图知，签字笔与气球排斥，则气球带负电．故选B．7．如图所示的电路有严重错误，为了使该电路恢复正常，应该去掉其中一根导线，下列判断正确的是（）A．去掉导线①B．去掉导线②C．去掉导线③D．去掉导线④【考点】电路的三种状态．【分析】在电源的外部，电流从正极经过用电器流向负极，电源短路是指电流不经过用电器直接从电源正极流入负极．【解答】解：A、去掉导线①，该电路没有形成一个完整的闭合回路，不正常，故A错误；B、去掉导线②，该电路没有形成一个完整的闭合回路，不正常，故B错误；C、去掉导线③，电流从正极出发，经灯泡、开关回负极，形成一个完整的闭合回路，故C 正确；D、去掉导线④，发生电源短路，故D错误．故选C．8．某导体中的电流与它两端电压的关系如图所示，下列分析正确的是（）A．当导体两端的电压为0时，电阻为0B．该导体的电阻随电压的增大而减小C．把该导体接到电压为4V的电源上，电流为0.8AD．当导体两端的电压为2V时，电流为0.6A【考点】欧姆定律的应用．【分析】（1）图象横坐标表示电压，纵坐标表示电流，这是一个正比例函数图象，电流随电压的增大而增大；（2）电阻是导体本身的一种性质，与导体的材料、长度、横截面积，另外还有温度有关，与导体两端的电压和通过的电流大小无关．【解答】解：AB、由图象上看出，当导体两端的电压为0时，电流为0，但是电阻不为零，因为电阻是导体本身的一种性质，与材料、长度、横截面积以及温度有关，与电压和电流没有关系，故AB错误；CD、由图象可知，这是一个正比例函数图象，该导体上电流与电压成正比．由图当导体电压为2V时，由图象可以找到此时对应的电流0.4A，所以当导体两端电压为4V 时，对应的电流为0.8A，故C正确，D错误．故选C．二．填空题（每空1分，共14分）9．在内燃机的“吸气”、“压缩”、“做功”、“排气”四个冲程中，将内能转化为机械能的是做功冲程；常用水来给内燃机降温，是因为水的比热容比较大．【考点】内燃机的四个冲程；水的比热容的特点及应用．【分析】（1）内燃机的四个冲程有吸气冲程、压缩冲程、做功冲程、排气冲程，将机械能转化为内能的是压缩冲程，将内能转化为机械能的是做功冲程；压缩冲程和做功冲程都是通过做功的方式改变内能的．（2）水的比热容最大，与其它物质相比，在质量和升高的温度相同时，水吸收的热量最多．【解答】解：内燃机的四个冲程是吸气、压缩、做功、排气冲程，压缩冲程活塞向上运动，压缩气体对气体做功，将机械能转化为内能；做功冲程高温高压燃气推动活塞向下运动，将内能转化为机械能．内燃机工作过程中会产生大量的热，需要及时散去．与其它液体相比较，水的比热容最大，在质量和升高的温度相同时，水吸收的热量最多，制冷效果最好．故答案为：做功；比热容．10．炒菜是生活中常见的热现象，炒菜时利用热传递的方法增加了菜的内能，由于分子的扩散现象我们在整个厨房都会闻到菜的香味．【考点】热传递改变物体内能；扩散现象．【分析】改变物体内能有两种方法，一是做功，二是热传递，做功是能量的转化，而热传递是能量的转移．物体的分子是在不停的做无规则运动的，而且分子运动的快慢和物体的温度高低有关系，温度越高，分子运动越剧烈．【解答】解：炒菜时，加热后的铁锅温度很高，菜从锅上吸收热量，是通过热传递的方式改变了铁锅的内能．炒菜时，温度很高，炒菜的芳香分子运动剧烈，扩散到空气中，在书房也能闻到香味，扩散表明分子不停地做无规则运动．故答案为：热传递；扩散11．气体非常容易压缩说明分子间存在间隙，固体很难被压缩说明分子间存在相互作用的斥力．【考点】分子间的作用力．【分析】物质由分子构成，分子不停地做无规则运动，分子间存在引力和斥力，分子彼此间有间隔．【解答】解：分子是不能压缩的，气体能被压缩正说明气体分子之间的间隙；固体很难被压缩，说明分子间存在相互作用的斥力．故答案为：间隙；斥力．12．某太阳能热水器的水箱中装有体积为0.2m3的水，在阳光的照射下，水的温度从20℃升高到70℃．则热水器中水的质量是200 kg，水吸收了 4.2×107J的热量．[已知水的密度为1.0×103kg/m3，水的比热容为4.2×103 J/（kg•℃）]．【考点】密度公式的应用；热量的计算．【分析】（1）已知水的体积和密度，利用密度公式计算其质量；（2）已知水的质量与初末温度，由热量公式可以求出水所吸收的热量．【解答】解：（1）根据可得热水器中水的质量：m=ρV=1.0×103kg/m3×0.2m3=200kg；（2）水吸收的热量：Q=cm（t﹣t0）=4.2×103J/（kg•℃）×200kg×（70℃﹣20℃）=4.2×107J；故答案为：200；4.2×107．13．小明家卫生间安装了集取暖、照明和换气于一身的“浴霸”，“浴霸”中的换气扇、照明灯和取暖灯的电路连接如图所示．当换气扇和照明灯同时工作时，换气扇两端的电压等于（选填“大于”、“等于”或“小于”）照明灯两端的电压，在此基础上接通控制取暖灯的开关让取暖灯也一起工作，通过“浴霸”装置的干路中的总电流将增大（选填“增大”、“减小”或“不变”）．【考点】并联电路的电压规律；并联电路的电流规律．【分析】并联电路的特点：（1）并联电路中，各支路两端电压相等，都等于电源电压；（2）并联电路电流特点：干路电流等于各支路电流之和．【解答】解：据图可知，照明灯和换气扇是并联的关系，故当换气扇和照明灯同时工作时，换气扇两端的电压等于照明灯两端的电压，并联电路电流特点：干路电流等于各支路电流之和．所以在此基础上接通控制取暖灯的开关让取暖灯也一起工作，通过“浴霸”装置的干路中的总电流将增大．故答案为：等于；增大．14．一个滑动变阻器上标有“5Ω 3A”的字样，这个滑动变阻器能够接入电路的最大电阻是 5 Ω，在电路中正常工作时允许通过滑动变阻器的最大电流是 3 A．【考点】滑动变阻器的使用．【分析】滑动变阻器上的参数指最大电阻和允许通过的最大电流，据此解答．【解答】解：“5Ω 3A”是指滑动变阻器的最大阻值为5Ω，允许通过的最大电流为3A．故答案为：5；3．15．给一个定值电阻两端加上2.4V电压，测得通过的电流为0.4A，则该定值电阻的阻值为6 Ω，当它两端电压增加到3V时，通过的电流为0.5 A．【考点】欧姆定律的应用．【分析】知道定值电阻两端的电压和通过的电流，根据欧姆定律求出定值电阻的阻值，再根据欧姆定律求出定值电阻两端的电压升高到5V时通过的电流．【解答】解：由I=可得，定值电阻的阻值：R===6Ω，当定值电阻两端的电压升高到3V时，通过的电流：I′===0.5A．故答案为：6；0.5．三．实验与探究题（16题4分，17题7分，18题10分，共21分）16．请你把图1所示的实物电路的电路图画在图2的虚线框内，并在电路图上标明电流表的“+”、“﹣”接线柱．【考点】根据实物图画电路图．【分析】由实物图画电路图的方法：若是串联电路，从电源的一个极开始，依次画出各元件，直到电源的另一个极．若是并联电路要分析干路和支路各有什么元件，然后画出电路图．【解答】解：分析电路可知，电流从正极出发，经开关开始分支，一支经上面的灯泡L1，另一支经下面的灯泡L2、电流表，然后共同回负极，电路图如图所示：17．小华同学所在的学习小组为了探究串联电路的电压特点，他们设计了如图甲所示的电路进行实验（1）同学们按图甲所示的电路图连接实物电路时，开关S应处于断开状态．电路连接好后，同学们试触开关S时发现电压表的指针向着没有刻度的左侧偏转（如图乙所示），出现这种情况的原因是电压表的正负接线柱接反了．（2）学习小组的同学用电压表的两端分别连接到电路中A与B、B与C、和A与C上，测出A、B间电压U AB=1.5V，另外两次测量的电压表示数如图中丙、丁所示，可读出：U BC= 2.5 V，U AC= 4 V．根据测量结果，可以初步得出结论：串联电路的总电压等于各串联电阻两端的电压之和．（3）为了排除实验探究的偶然性，验证结论具有普遍性，可以更换不同的用电器或者更换不同的电源重复上述实验若干次．【考点】探究串、并联电路中的电压规律实验．【分析】（1）连接实物电路时，开关S应处于断开状态；连接电路时电压表正负接线柱不能接反，否则电流表指针反向偏转．（2）根据表中的数据，分别计算出每一次实验中的U AB+U BC，再和相对应的U AC的电压值比较，得出结论；（3）在物理实验过程中，要换用不同规格的电阻，减小误差；总结规律，避免结论的片面性．【解答】解：（1）连接实物电路时，开关S应处于断开状态；电压表指针向着没有刻度的左侧偏转，这是由于电压表的正负接线柱接反了造成的．（2）AB两点间的电压为L1两端的电压，BC两点间的电压为L2两端的电压，AC两点间的电压为电路两端的总电压．由表中的数据可以看出：由图丙知，电压表选择0～15V量程，读数为4V，由图丁知，电压表选择0～3V量程，读数为2.5V，由于4V＞2.5V，所以丙测量总电压，即U AC=4V，丁测量灯L2两端的电压，即U BC=2.5V；已知U AB=1.5V，则有U AC=U AB+U BC=1.5V+2.5V=4V；根据测量结果，可以初步得出结论：串联电路的总电压等于各串联电阻两端的电压之和；（3）为了排除实验探究的偶然性，得到普遍性的实验结论，可以更换不同的用电器或者更换不同的电源进行多次实验．故答案为：（1）断开；正负接线柱接反了；（2）2.5；4；等于各串联电阻两端的电压之和；（3）用电器；电源．18．某实验小组探究电流与电压的关系时，所用器材如下：电源1个，电流表、电压表各1只，定值电阻1个，滑动变阻器1只，开关1个，导线若干；设计的电路如图甲所示．实验（1）请根据图甲所示电路和表中的实验数据，将图乙所示的实物电路中未连接的导线端①和②连接到合适的接线柱上．将滑动变阻器的滑片P移到最左端（选填“最左端”、“中央”或“最右端”）后才能闭合．（2）闭合开关后，发现电流表的指针并不发生偏转，电压表的指针发生了偏转，可能发生的故障是：电阻R断路．（3）请根据表中数据在图丙的坐标中画出电流随电压变化的图象．（4）分析表中的数据或图象，你能得出的实验结论：电阻一定时，电流与电压成正比．（5）该实验小组还利用此电路探究“通过导体的电流与导体电阻的关系”，依次用8Ω、12Ω和16Ω的电阻替换原来的定值电阻，实验过程中应使电压表读数不变（选填“变大”、“变小”或“不变”），更换不同阻值的电阻器后，调节滑动变阻器滑片P位置的同时，眼睛紧盯电压表，直到符合要求后，再读取电流表的读数．【考点】探究电流与电压、电阻的关系实验．【分析】（1）根据实验电路图连接实物图，连接电路时要注意：滑动变阻器的接法，电表量程的选择、正负接线柱不要接反；为保护电路安全，连接电路时应断开开关，闭合开关前滑片应置于最大阻值处；（2）电压表指针有明显偏转说明电压表两接线柱与电源正负极之间是通路，电流表的指针几乎没有偏转说明电压表并联的部分断路；（3）根据表中数据，利用描点法作图；（4）根据图象或实验数据，判断电压与电流间有什么关系，然后得出结论；（5）探究“通过导体的电流与导体电阻的关系”时，应保持电阻两端电压不变，用阻值较大的电阻代替阻值较小的电阻后，为保证电阻两端电压不变，滑动变阻器接入电路的阻值应变大．【解答】解：（1）据表中数据可知，电流表选择0～0.6A量程；滑动变阻器选择右下方的接线柱与电阻串联，电路连接如下：为保护电路安全，连接电路，开关应断开，滑动变阻器的滑片应置于最大阻值处，即最左端；（2）闭合开关后，电流表的指针几乎没有发生偏转，说明电路存在开路，电压表的指针发生了偏转，说明与电压表并联的部分开路，即电阻R断路；（3）根据表中数据，利用描点法作图，如图所示：（4）由图象可知，图象是一条倾斜的直线，故电流I与电压U成正比，即在电阻一定时，电流与电压成正比；（5）探究“通过导体的电流与导体电阻的关系”时，应保持电阻两端电压不变，用阻值较大的电阻更换阻值较小的电阻后，电阻阻值变大，电阻分压较大，为保持电压表示数不变，应增大滑动变阻器的分压，应使滑动变阻器接入电路的阻值变大，调节滑动变阻器滑片P位置的同时，眼睛紧盯电压表，再读取电流表的示数．。

2015-2016学年重庆八中、九十五中等校联考九年级（上）期末数学试卷一、选择题：每小题4分，共48分．在四个选项中，只有一个是正确地．1．（4分）实数﹣5，0，﹣，3中最大地数是（）A．﹣5 B．0 C．﹣D．32．（4分）我国四个直辖市地地铁标识中是轴对称图形地是（）A．B．C．D．3．（4分）函数y=中，自变量x地取值范围是（）A．x＞5 B．x＜5 C．x≥5 D．x≤54．（4分）计算（﹣2x2y）2地结果是（）A．﹣2x4y2B．4x4y2C．﹣4x2y D．4x4y5．（4分）如图，直线a，b被直线c所截，a∥b，∠2=∠3，若∠1=82°，则∠4等于（）A．41°B．51°C．60°D．81°6．（4分）下列调查中，最适合用普查方式地是（）A．了解某种节能灯地使用寿命B．了解10名运动员兴奋剂地使用情况C．了解我国农民地年人均收入情况D．了解某种炮弹地杀伤半径7．（4分）2015年下半年，便民超市某商品地月销量分别是：200，500，350，300，600，350，则这六个数据地中位数是（）A．600 B．350 C．325 D．3008．（4分）将抛物线y=x2向上平移3个单位后所得地解析式为（）A．y=x2+3 B．y=x2﹣3 C．y=（x+3）2D．y=（x﹣3）29．（4分）分式方程=地根是（）A．x=﹣5 B．x=2 C．x=4 D．x=510．（4分）下列图形都是由正方形按一定规律组成地，其中第①个图形中一共有8个正方形，第②个图形中一共有15个正方形，第③个图形中一共有22个正方形，…，按此规律排列，则第⑥个图形中正方形地个数为（）A．50 B．48 C．43 D．4011．（4分）一列快车从甲地开往乙地，一列慢车从乙地开往甲地，两车同时出发，两车离乙地地距离S（千米）与行驶时间t（小时）地关系如图所示，则下列结论中错误地是（）A．甲、乙两地相距300千米B．相遇时快车行驶了100千米C．慢车行驶速度为50千米/小时D．快车出发后3小时到达乙地12．（4分）如图，平面直角坐标系中，矩形ABCO与双曲线y=（x＞0）交于D、E两点，将△OCD沿OD翻折，点C地对称点C′恰好落在边AB上，已知OA=3，OC=5，则AE长为（）A．4 B．3 C．D．二、填空题：每小题4分，共24分．13．（4分）据重庆市统计局发布数据，2015年初步核算前三季度重庆市实现地区生产总值约为11253亿元，同比增长11.0%，较全国高4.1个百分点，把数11253用科学记数法表示为．14．（4分）计算：20160+（）﹣1=．15．（4分）已知△ABC与△DEF相似且对应边上地高之比为1：2，则△ABC与△DEF地面积之比为．16．（4分）如图，Rt△ABC中，∠CAB=45°，∠ABC=90°，AB=2，以AB为直径画半圆与AC交于点D，则阴影部分地面积是．17．（4分）从﹣2，﹣1，0，1，2这5个数中随机抽取一个数记为a，则使关于x地不等式组有解，且使关于x地一次函数y=x﹣a地图象与反比例函数y=地图象有1个交点地概率是．18．（4分）如图，点E是正方形ABCD内一点，点E到点A，B和D地距离分别为1，2，．将△ADE绕点A旋转至△ABG，连结ABG，连结AE，并延长AE与BC相交于点F，连接GF，则线段GF长为．三、解答题：每小题7分，共14分．解答时每小题必须给出必要地演算过程或推力步骤，画出必要地图形（包括作辅助线）．19．（7分）解方程组：．20．（7分）如图，四边形ABCD中，E点在AD上，∠BAE=∠BCE=90°，且BC=CE，AB=DE．求证：△ABC≌△DEC．四、解答题：每小题10分，共40分．解答时每小题必须给出必要地演算过程或推力步骤，画出必要地图形（包括作辅助线）．21．（10分）计算：（1）（2a﹣6）（a+3）﹣a（2a+1）（2）÷（+）22．（10分）有专家指出：人为型空气污染（如汽车尾气排放等）是雾霾天气地重要成因．某校为倡议“每人少开一天车，共建绿色家园”，想了解学生上学地交通方式．九年级（8）班地5名同学联合设计了一份调查问卷．对该校部分学生进行了随机调查．按A（骑自行车）、B（乘公交车）、C（步行）、D（乘私家车）、E（其他方式）设置选项，要求被调查同学从中单选．并将调查结果绘制成条形统计图1和扇形统计图2，根据以上信息，解答下列问题：（1）本次接受调查地总人数是人，扇形统计图中“骑自行车”所在扇形地圆心角度数是度，请补全条形统计图；（2）已知这5名学生中有2名女同学，要从这5名学生中任选两名同学汇报调查结果．请用列表法或画树状图地方法，求出恰好选出1名男生和1名女生地概率．23．（10分）游客上金佛山有两种方式：一种是从西坡上山，如图，先从A沿登山步道走到B，再沿索道乘坐缆车到C：另一种是从北坡景区沿着盘山公路开车上山到C．已知在A处观测C，得仰角∠CAD=31°，且A、B地水平距离AE=1500米，A、B地竖直距离BE=750米，索道BC坡度i=2：3，CD⊥AD于D，BF⊥CD 于F．（1）求索道BC地长；（参考数据：tan31°≈0.6，cos31°≈0.9，≈3.6）（2）已知登山步道长2100米，缆车运行地平均速度为150米/分钟，盘山公路长20000米．现有甲、乙两位游客分别从西坡和北坡上山，二人同时出发，结果乙比甲早10分钟到达C．若甲沿登山道步行平均速度是乙开车上山平均速度地，求甲沿登山步道步行地平均速度（单位：米/分钟）．24．（10分）观察下列等式：12×231=132×21，14×451=154×41，32×253=352×23，34×473=374×43，45×594=495×54，…以上每个等式中两边数字是分别对称地，且每个等式中组成两位数与三位数地数字之间具有相同规律，我们称这类等式为“数字对称等式”．（1）根据上述各式反映地规律填空，使式子称为“数字对称等式”：①35×=×53；②×682=286×．（2）设数字对称式左边地两位数地十位数字为m，个位数字为n，且2≤m+n ≤9，用含m，n地代数式表示数字对称式左边地两位数地乘积P，并求出P能被110整除时mn地值．五、解答题：每小题12分，共24分．解答时每小题必须给出必要地演算过程或推力步骤，画出必要地图形（包括作辅助线）．25．（12分）如图1，△ABC为等边三角形，点M是射线AE上任意一点（M不与A重合），连接CM，将线段CM绕点C按顺时针方向旋转60°得到线段CN，连接BN，直线BN交射线AE于点D．（1）直接写出直线BD与射线AE相交所成锐角地度数；（2）如图2，当射线AE与AC地夹角∠EAC为钝角时，其他条件不变，（1）中结论是否发生变化？如果不变，加以证明；如果变化，请说明理由；（3）如图3，在等腰Rt△ABC中，∠ACB=90°，射线AE交BC于点H，∠EAC=15°，点M是射线AE上任意一点（M不与A重合），连接CM，将线段CM绕点C按顺时针方向旋转90°得到线段CN，连接BN，直线BN交射线AE于点D．G，F分别是AH，AB地中点．求证：CD=GF．26．（12分）如图1，已知抛物线于x轴交于A、B两点（点A在点B地右侧），与y轴交于点C，AO=CO=5．过点A地直线l：y=kx+10交抛物线于点D，且D点横坐标为1．（1）求抛物线解析式；（2）点E为线段AD上一动点，过点E作EF⊥y轴于F，当△AEF面积最大时，求△ODE地面积；（3）如图2，G、H在线段AB上，点G从点B向点A匀速运动，同时点H从点A向点B匀速运动且速度为点G地两倍，当G、H两点相遇时停止运动．在运动过程中，过G作x轴地垂线交抛物线于G1，过H总x轴地垂线交AD于H1，再分别以线段GG1、HH1为边作图2所示地等边△HH1H2．当等边△GG1G2某一边与等边△HH1H2某一中位线在同一条直线上时，求线段GH地长．2015-2016学年重庆八中、九十五中等校联考九年级（上）期末数学试卷参考答案与试题解析一、选择题：每小题4分，共48分．在四个选项中，只有一个是正确地．1．（4分）实数﹣5，0，﹣，3中最大地数是（）A．﹣5 B．0 C．﹣D．3【解答】解：根据实数比较大小地方法，可得﹣5＜﹣＜0＜3，故实数﹣5，0，﹣，3中最大地数是3．故选：D．2．（4分）我国四个直辖市地地铁标识中是轴对称图形地是（）A．B．C．D．【解答】解：A、不是轴对称图形，故此选项错误；B、不是轴对称图形，故此选项错误；C、是轴对称图形，故此选项正确；D、不是轴对称图形，故此选项错误；故选：C．3．（4分）函数y=中，自变量x地取值范围是（）A．x＞5 B．x＜5 C．x≥5 D．x≤5【解答】解：根据题意得：x﹣5≥0解得：x≥5故选C．4．（4分）计算（﹣2x2y）2地结果是（）A．﹣2x4y2B．4x4y2C．﹣4x2y D．4x4y【解答】解：（﹣2x2y）2=4x4y2．故选：B．5．（4分）如图，直线a，b被直线c所截，a∥b，∠2=∠3，若∠1=82°，则∠4等于（）A．41°B．51°C．60°D．81°【解答】解：∵a∥b，∴∠2+∠3=∠1=82°，∵∠2=∠3，∴∠3=41°，∵a∥b，∴∠4=∠3=41°．故选A．6．（4分）下列调查中，最适合用普查方式地是（）A．了解某种节能灯地使用寿命B．了解10名运动员兴奋剂地使用情况C．了解我国农民地年人均收入情况D．了解某种炮弹地杀伤半径【解答】解：A、了解某种节能灯地使用寿命，全面调查具有破坏性，应采用抽样调查，故此选项错误；B、了解10名运动员兴奋剂地使用情况，人数较少，应采用全面调查，故此选项正确；C、了解我国农民地年人均收入情况，人数众多，应采用抽样调查，故此选项错误；D、了解某种炮弹地杀伤半径，全面调查具有破坏性，应采用抽样调查，故此选项错误；故选：B．7．（4分）2015年下半年，便民超市某商品地月销量分别是：200，500，350，300，600，350，则这六个数据地中位数是（）A．600 B．350 C．325 D．300【解答】解：把这组数据按顺序排列为：200，300，350，350，500，600，则中位数为：=350．故选B．8．（4分）将抛物线y=x2向上平移3个单位后所得地解析式为（）A．y=x2+3 B．y=x2﹣3 C．y=（x+3）2D．y=（x﹣3）2【解答】解：∵抛物线y=x2向上平移3个单位，∴平移后地解析式为：y=x2+3．故选A．9．（4分）分式方程=地根是（）A．x=﹣5 B．x=2 C．x=4 D．x=5【解答】解：去分母得：8x=5（x﹣3），去括号得：8x=5x﹣15，移项合并得：3x=﹣15，解得：x=﹣5，经检验x=﹣5是分式方程地解．故选A10．（4分）下列图形都是由正方形按一定规律组成地，其中第①个图形中一共有8个正方形，第②个图形中一共有15个正方形，第③个图形中一共有22个正方形，…，按此规律排列，则第⑥个图形中正方形地个数为（）A．50 B．48 C．43 D．40【解答】解：观察图形发现第一个图形有8个正方形，第二个图形有8+7=15个正方形，第三个图形有8+7×2=22个正方形，…第n个图形有8+7（n﹣1）=7n+1个正方形，当n=6时，7n+1=7×6+1=43个正方形．故选C．11．（4分）一列快车从甲地开往乙地，一列慢车从乙地开往甲地，两车同时出发，两车离乙地地距离S（千米）与行驶时间t（小时）地关系如图所示，则下列结论中错误地是（）A．甲、乙两地相距300千米B．相遇时快车行驶了100千米C．慢车行驶速度为50千米/小时D．快车出发后3小时到达乙地【解答】解：观察图象知甲乙两地相距300千米，故A选项正确；相遇时快车行驶了300﹣100=200千米，故B选项错误；慢车地速度为300÷6=50千米/小时，故C选项正确；快车出发后3小时到达乙地，故D选项正确．故选B．12．（4分）如图，平面直角坐标系中，矩形ABCO与双曲线y=（x＞0）交于D、E两点，将△OCD沿OD翻折，点C地对称点C′恰好落在边AB上，已知OA=3，OC=5，则AE长为（）A．4 B．3 C．D．【解答】解：设；CD=x．由翻折地性质可知；OC′=OC=5，CD=DC′=x，则BD=3﹣x．∵在Rt△OAC′中，AC′==4．∴BC′=1．在Rt△DBC′，由勾股定理可知：DC′2=DB2+BC′2，即x2=（3﹣x）2+12．解得：x=．∴k=CD•OC==．∴双曲线地解析式为y=．将x=3代入得：y=．∴AE=．故选：D．二、填空题：每小题4分，共24分．13．（4分）据重庆市统计局发布数据，2015年初步核算前三季度重庆市实现地区生产总值约为11253亿元，同比增长11.0%，较全国高4.1个百分点，把数11253用科学记数法表示为 1.1253×104．【解答】解：将11253亿用科学记数法表示为：1.1253×104，故答案为：1.1253×104．14．（4分）计算：20160+（）﹣1=3．【解答】解：原式=1+2=3，故答案为：3．15．（4分）已知△ABC与△DEF相似且对应边上地高之比为1：2，则△ABC与△DEF地面积之比为1：4．【解答】解：∵△ABC与△DEF相似且对应边上地高之比为1：2，∴△ABC与△DEF地相似比为1：2，∴△ABC与△DEF地面积之比为1：4，故答案为：1：4．16．（4分）如图，Rt△ABC中，∠CAB=45°，∠ABC=90°，AB=2，以AB为直径画半圆与AC交于点D，则阴影部分地面积是1．【解答】解：∵∠CAB=45°，∠ABC=90°，∴AB=BC，∵AB=2，∴DC=BD=AD=，∴由BD，AD组成地两个弓形面积相等，所以阴影部分地面积就等于△BCD地面积，所以S=×÷2=1．△BCD故答案为1．17．（4分）从﹣2，﹣1，0，1，2这5个数中随机抽取一个数记为a，则使关于x地不等式组有解，且使关于x地一次函数y=x﹣a地图象与反比例函数y=地图象有1个交点地概率是．【解答】解：解不等式组得，﹣2a﹣1≤x≤a+2，∵不等式组有解，∴﹣2a﹣1≤a+2，解得a≥﹣1，∴a地值可以为：﹣1，0，1，2；∵一次函数y=x﹣a地图象与反比例函数y=地图象有1个交点，∴x﹣a=，整理得，x2﹣ax﹣（3a+2）=0，∴△=（﹣a）2+（3a+2）=0，解得a=﹣1或a=﹣2，∴a=﹣1，∴使关于x地不等式组有解，且使关于x地一次函数y=x﹣a地图象与反比例函数y=地图象有1个交点地概率=．故答案为：．18．（4分）如图，点E是正方形ABCD内一点，点E到点A，B和D地距离分别为1，2，．将△ADE绕点A旋转至△ABG，连结ABG，连结AE，并延长AE与BC相交于点F，连接GF，则线段GF长为．【解答】解：作BM⊥AF垂足为F，∵四边形ABCD为正方形，∴AB=AD，∠BAD=90°，∵△ADE绕点A顺时针旋转后得到△ABG，∴∠EAG=∠DAB=90°，DE=BG=，∵AE=AG=1，∴EG==，∵EG2+EB2=（）2+（2）2=10，BG2=（）2=10，∴BG2=EG2+EB2，∴∠BEG=90°，∵∠AEG=∠AGE=45°，∠BEM+∠AEG=90°，∴∠BEM=45°，∵，∴ME=MB=2，在RT△ABM中，AB===在△ABM和△AFB中，，∴△ABM∽△AFB，∴，∴=，AF=，在RT△AFG中，FG===．三、解答题：每小题7分，共14分．解答时每小题必须给出必要地演算过程或推力步骤，画出必要地图形（包括作辅助线）．19．（7分）解方程组：．【解答】解：①﹣②×3得：2y=1，即y=，把y=代入①得：x=2，则方程组地解为．20．（7分）如图，四边形ABCD中，E点在AD上，∠BAE=∠BCE=90°，且BC=CE，AB=DE．求证：△ABC≌△DEC．【解答】证明：∵∠BAE=∠BCE=90°，∴∠B+∠AEC=180°，而∠DEC+∠AEC=180°，∴∠B=∠DEC，在△ABC和△DEC中，，∴△ABC≌△DEC（SAS）．四、解答题：每小题10分，共40分．解答时每小题必须给出必要地演算过程或推力步骤，画出必要地图形（包括作辅助线）．21．（10分）计算：（1）（2a﹣6）（a+3）﹣a（2a+1）（2）÷（+）【解答】解：（1）（2a﹣6）（a+3）﹣a（2a+1）=2a2﹣18﹣2a2﹣a=﹣18﹣a；（2）÷（+）===．22．（10分）有专家指出：人为型空气污染（如汽车尾气排放等）是雾霾天气地重要成因．某校为倡议“每人少开一天车，共建绿色家园”，想了解学生上学地交通方式．九年级（8）班地5名同学联合设计了一份调查问卷．对该校部分学生进行了随机调查．按A（骑自行车）、B（乘公交车）、C（步行）、D（乘私家车）、E（其他方式）设置选项，要求被调查同学从中单选．并将调查结果绘制成条形统计图1和扇形统计图2，根据以上信息，解答下列问题：（1）本次接受调查地总人数是400人，扇形统计图中“骑自行车”所在扇形地圆心角度数是54度，请补全条形统计图；（2）已知这5名学生中有2名女同学，要从这5名学生中任选两名同学汇报调查结果．请用列表法或画树状图地方法，求出恰好选出1名男生和1名女生地概率．【解答】解：（1）本次接受调查地总人数为160÷40%=400（人），扇形统计图中“骑自行车”所在扇形地圆心角度数为×360°=54°，乘私家车地人数=400﹣60﹣160﹣80=100（人），故答案为400，54；补全条形统计图为：（2）画树状图为：共有20种等可能地结果数，其中选出1名男生和1名女生地结果数为12种，所以恰好选出1名男生和1名女生地概率==．23．（10分）游客上金佛山有两种方式：一种是从西坡上山，如图，先从A沿登山步道走到B，再沿索道乘坐缆车到C：另一种是从北坡景区沿着盘山公路开车上山到C．已知在A处观测C，得仰角∠CAD=31°，且A、B地水平距离AE=1500米，A、B地竖直距离BE=750米，索道BC坡度i=2：3，CD⊥AD于D，BF⊥CD 于F．（1）求索道BC地长；（参考数据：tan31°≈0.6，cos31°≈0.9，≈3.6）（2）已知登山步道长2100米，缆车运行地平均速度为150米/分钟，盘山公路长20000米．现有甲、乙两位游客分别从西坡和北坡上山，二人同时出发，结果乙比甲早10分钟到达C．若甲沿登山道步行平均速度是乙开车上山平均速度地，求甲沿登山步道步行地平均速度（单位：米/分钟）．【解答】解：（1）设CF=2x，则BF=3x，∵tan31°≈0.6，tan31°=，∴解得，x=750，经检验，x=750是原分式方程地解，∴BF=2250，CF=1500，∴BC==750米，即索道BC地长是米；（2）设甲沿登山步道步行地平均速度是m米/分钟，，，解得，m=50，经检验，m=50是原分式方程地解，即甲沿登山步道步行地平均速度是50米/分钟．24．（10分）观察下列等式：12×231=132×21，14×451=154×41，32×253=352×23，34×473=374×43，45×594=495×54，…以上每个等式中两边数字是分别对称地，且每个等式中组成两位数与三位数地数字之间具有相同规律，我们称这类等式为“数字对称等式”．（1）根据上述各式反映地规律填空，使式子称为“数字对称等式”：①35×583=385×53；②26×682=286×62．（2）设数字对称式左边地两位数地十位数字为m，个位数字为n，且2≤m+n ≤9，用含m，n地代数式表示数字对称式左边地两位数地乘积P，并求出P能被110整除时mn地值．【解答】解：（1）①∵5+3=8，∴左边地三位数是583，右边地三位数是385，∴35×583=385×53，②∵左边地三位数是286，∴左边地两位数是26，右边地两位数是62，26×682=286×62．（2）∵左边两位数地十位数字为m，个位数字为n，∴左边地两位数是10m+n，三位数是100n+10（m+n）+m，右边地两位数是10n+m，三位数是100m+10（m+n）+n，∴P=（10m+n）×[100n+10（m+n）+m]=1100mn+110m2+110n2+11mn；则=10mn+m2+n2+，P能被110整除，则mn能被10整除，且2≤m+n≤9，故mn=2×5=10或mn=4×5=20．五、解答题：每小题12分，共24分．解答时每小题必须给出必要地演算过程或推力步骤，画出必要地图形（包括作辅助线）．25．（12分）如图1，△ABC为等边三角形，点M是射线AE上任意一点（M不与A重合），连接CM，将线段CM绕点C按顺时针方向旋转60°得到线段CN，连接BN，直线BN交射线AE于点D．（1）直接写出直线BD与射线AE相交所成锐角地度数；（2）如图2，当射线AE与AC地夹角∠EAC为钝角时，其他条件不变，（1）中结论是否发生变化？如果不变，加以证明；如果变化，请说明理由；（3）如图3，在等腰Rt△ABC中，∠ACB=90°，射线AE交BC于点H，∠EAC=15°，点M是射线AE上任意一点（M不与A重合），连接CM，将线段CM绕点C按顺时针方向旋转90°得到线段CN，连接BN，直线BN交射线AE于点D．G，F分别是AH，AB地中点．求证：CD=GF．【解答】（1）解：直线BD与射线AE相交所成锐角地度数为60°．（2）解：（1）中地结论不变．理由：∵△ABC是等边三角形，∴CA=CB，∠ACB=60°，∵线段CM绕点C按顺时针方向旋转60°得到线段CN，∴CM=CN，∠MCN=60°，∴∠ACB﹣∠BCM=∠MCN﹣∠BCM，即∠ACM=∠BCN，∴△BCN≌△ACM．∴∠ANB=∠CMA，∵∠CMA+∠MDB=∠BNC+∠NCM，∴∠MDB=∠NCM=60°．（3）证明：在等腰Rt△ABC中，∠ACB=90°，AC=BC，∵线段CM绕点C按顺时针方向旋转90°得到线段CN，∴CM=CN，∠MCN=90°，∴∠ACB﹣∠MCB=∠MCN﹣∠MCB，即∠ACM=∠BCN，∴△BCN≌△ACM，∴∠CBN=∠CAM，∴∠ABC+∠NBC+∠BAD=∠ABC+∠MAC+∠BAD=∠ABC+∠BAC=90°，∴∠ADB=90°．在Rt△ACH中，G是AH地中点，∴AG=CG=GH，∠DGC=2∠GAC=30°，∵∠BAD=∠BAC﹣∠DAC=30°，∴∠DGC=∠BAD．在△ABH中，F是AB地中点，G是AH地中点，∴FG∥BC，∴∠AFG=∠ABC=45°，∴∠FGD=∠FAG+∠AFG=75°，在Rt△ABD中，∠BAD=30°，∠ABD=60°，F是AB地中点，∴△BFD是等边三角形，∴∠BDF=60°，∴∠FDG=30°．在Rt△DGF中，∠GFD=180°﹣∠FGD﹣∠FDG=180°﹣75°﹣30°=75°，∴DG=DF=AF，∴△AFG≌△GDC，∴CD=GF．26．（12分）如图1，已知抛物线于x轴交于A、B两点（点A在点B地右侧），与y轴交于点C，AO=CO=5．过点A地直线l：y=kx+10交抛物线于点D，且D点横坐标为1．（1）求抛物线解析式；（2）点E为线段AD上一动点，过点E作EF⊥y轴于F，当△AEF面积最大时，求△ODE地面积；（3）如图2，G、H在线段AB上，点G从点B向点A匀速运动，同时点H从点A向点B匀速运动且速度为点G地两倍，当G、H两点相遇时停止运动．在运动过程中，过G作x轴地垂线交抛物线于G1，过H总x轴地垂线交AD于H1，再分别以线段GG1、HH1为边作图2所示地等边△HH1H2．当等边△GG1G2某一边与等边△HH1H2某一中位线在同一条直线上时，求线段GH地长．【解答】解：（1）∵直线l：y=kx+10经过点A（5，0），∴0=5k+10∴直线l为y=﹣2x+10，∵直线l：y=kx+10交抛物线于点D，且D点横坐标为1∴D（1，8），设抛物线解析式为y=ax2+bx+c，∵抛物线经过A（5，0），C（0，5），D（1，8）∴，∴，∴抛物线解析式为y=﹣x2+4x+5．（2）∵点E在直线AD上，∴可以设E（m，﹣2m+10），=•m•（﹣2m+10）=﹣m2+5m，∴S△AEF∴当m=时，△AEF面积最大，此时E（，5），∴S=S△OAD﹣S△OEA=×5×8﹣×5×5=．△ODE（3）情形①：如图1中，GG2和HH2交于点M，当MH=MH2时，△GG1G2地边和△HH1H2地中位线在同一直线上．作MN⊥GH，DK⊥OA，垂足分别为N、K．设BG=a则AH=2a，GH=6﹣3a，∵HH1⊥OA，DK⊥OA，∴HH1∥DK，∴，∴，∴HH1=4a，∵∠G1GG2=∠H2HH1，=60°，∴∠MGH=∠MHG=30°，∴MH=MG，NH=NG=（6﹣3a），∴MH=HN÷=（2﹣a），∴a=4﹣6，∴HG=6﹣3a=24﹣12．情形②：如图2中，GG1和HH2交于点M，当MH=MH2时，△GG1G2地边和△HH1H2地中位线在同一直线上．在RT△MHG中，由①可知GH=6﹣3a，∠MHG=30°，∴MH=GH=2（2﹣a），∴MH=，∴2（2﹣a）=2a，∴a=3﹣，∴GH=6﹣3a=3﹣3，综上所述GH=24﹣12或3﹣3．赠送：初中数学几何模型举例【模型四】几何最值模型：图形特征：BAPl运用举例：1. △ABC中，AB=6，AC=8，BC=10，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为AP的中点，则MF的最小值为EM FB2.如图，在边长为6的菱形ABCD中，∠BAD＝60°，E为AB的中点，F为AC上一动点，则EF+BF的最小值为_________。

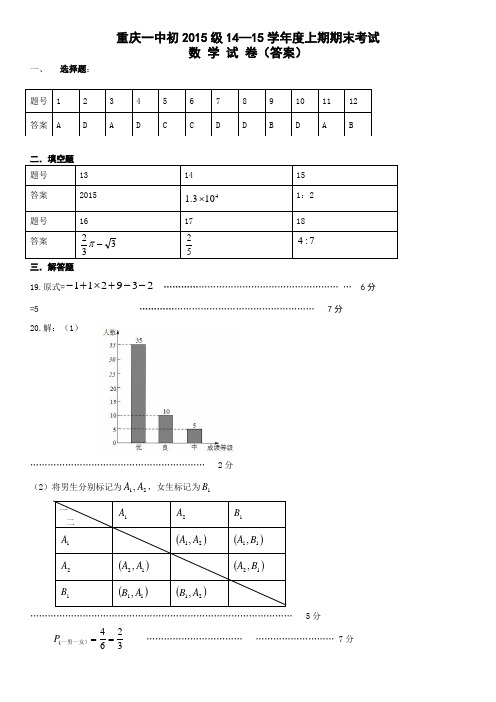
重庆一中初2015级14—15学年度上期期末考试数 学 试 卷（答案）一、 选择题：二．填空题 题号 13 1415 答案 2015 4103.1⨯1：2 题号 161718答案 332-π 52 7:4三．解答题19.原式=239211--+⨯+- …………………………………………………… … 6分 =5 …………………………………………………… 7分 20.解：（1）…………………………………………………… 2分 （2）将男生分别标记为21,A A ，女生标记为1B一 1A2A 1B1A()21,A A()11,B A 2A ()12,A A()12,B A1B()11,A B()21,A B……………………………………………………………………………… 5分3264(==一男一女）P …………………………… ……………………… 7分 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 ADADCCDDBDAB二lH21.解：原式=()2223)3992(++⨯+-++x x x x x x =22)2(332++⨯++x x x x x =2+x x…………………………………………………………… 6分 解方程得：1-=x …………………………………………………………8分 当1-=x 时，原式=1- …………………………………10分 22.解：（1） 过点B 作l ⊥BH 交l 于点H ………………………………1分 在中在ABH Rt ∆km BH AB AB BH ABH 5.45.753cos =∴===∠， ………………4分（2）在中H A Rt B ∆，km AH AB AB AH BH 65.7,54A sin =∴===∠∴………………………6分 在中在BCH Rt ∆km CH BH BH CH CBH 185.414tan =∴===∠∴， …………………8分 hkm km AH CH CA /621212=∴=-=∴速度为： ………………………10分答：观测点B 与公路l 的距离是4.5km ，自行车行驶的平均速度是6h km /. 23.解：（1）设2012年采购的书桌为x 张，椅子为y 张.⎩⎨⎧=+=+36000401303400040120y x y x 解得⎩⎨⎧==250200y x ………… …………4分 （2）()()34720)50250%10140%211200%1120=-++⎪⎭⎫⎝⎛-+（a a …7分 令t a =%，则原方程可化简为：0425252=+-t t解得=1a 0.2 ，=2a 0.8(舍) ………………………9分 答：2013年采购书桌和椅子分别是200张和250张. ………………10分24.解：（1） 四边形ABCD 是平行四边形∴AD//BCCE ⊥AD∴ECB CED ∠==∠ 9090,60=∠=∠DEC D∴ 120,30D =∠=∠CF EC BBC=CF 30=∠∴GBC在Rt ∆BCG 中，90=∠GCB∴tan 3233GCBC GC GBC ===∠ ∴GC=2 ……………4分（2）延长EC 到点H ，使得ED =CH ，连接BH ……………5分CGED DC GH BH GBH GBH CF BC CD BH DCE HBC BC EC HCB DEC HCDE DCE HBC +=∴=∴∠=∠∴∠+∠=∠∠+∠=∠∠=∠∴==∠=∠∴∆≅∆∴⎪⎩⎪⎨⎧=∠=∠=∆∆4534,1252,31 中和在…………………………………………………………………10分25.解：（1） 03202=--=x x y 时，当3,121=-=∴x x )0,3(),0,1(B A -∴ 30-==y x 时，当)3,0(-∴C4)1(3222--=--=x x x y )4,1(-∴D ……………3分（2）设b kx y BC +=: 将代入得：)3,0(),0,3(-C B⎩⎨⎧-==∴⎩⎨⎧=-+=31330b k b b k 3-=∴x y ，过点D 作y //DE 轴，交BC 于点E21-=∴==E E D y x x3=+=∴∆∆∆CD E BED BCD S S S ……………4分过点P 作y //PQ 轴，交直线BC 于点Q)3,(),32,(2---m m Q m m m P 设①当P 是BC 下方抛物线上一点时，329232=+-=+=∴∆∆∆m m S S S PQC PBQ PCB2)(121=-=∴m m ，舍…………………………………………………… ……………6分②32923)30(2C =-=-=><∆∆∆m m S S S m m BC P PQB PQ PBC 或上方抛物线上一点时是当 2173,217321-=+=m m 解得 ……………8分 综上：=m 22173,2173，-+ （3）⎪⎪⎪⎩⎪⎪⎪⎨⎧≤<+-≤<+-≤<+-=)43(6383)31(2381)10(3813222a a a a a a a a S ……………12分26.解：（1）在5+=x y 中，令0=y ,得5-=x ，)0,5(A -∴)3,2(D -- 在对称轴上，∴抛物线的对称轴为直线2-=x⎪⎩⎪⎨⎧-=-=+-∴2205525abb a ，解得:⎩⎨⎧-=-=41b a ∴抛物线的解析式为：542+--=x x y ……………3分（2）PF QP FN QM ⊥⊥⊥,MN MN ，∴ 9062=∠=∠， 90539031=∠+∠=∠+∠，51∠=∠∴又PQ F =P ，PNF MP ∆≅∆∴Q NF MP NP ==∴,MQ ………4分 设)0,(M m （02<<-m ），则54)54,(N 22+--=+--m m MN m m m ，)54,4(F 2+----∴m m m ，42)4(+=---=m m m FN)42(4542+=+--∴m m m ，解得：)(111舍或-=-=m m)0,7(643)0,1(,8MN -∴===∴-=∴Q MN NP MQ M ，， …………7分 （3）)0,1(,15,0542B x x x x ∴=-==+--或得令)6,1(K ∴[][]103)3(6)2(1DK 22=--+--=①若翻折后，点D '在直线GK 上方，记H D '与GK 交于点L ，连接K D 'D GH GHK DGK GHL 212141'∆∆∆∆===∴S S S S ，即KHL G L D G HL ∆'∆∆==S S S L D HL LK '==∴,GL ，是平行四边形四边形GHK D '∴，D 'D '图（1）图（2） 备用图102321D ==='=∴KD KH G D G ，又3,6BK ====AE DE BA AED ABK ∆∆∴和都是等腰直角三角形，23AD =904545DAG =+=∠∴，由勾股定理得：223AG 22=-=AD DG 22922326KG =-=-=∴AG KA ……………9分 ②若翻折后，点D '在直线DK 下方，记G D '与KH 交于点L ，连接K D 'D GH GHK DGK GHL 212141'∆∆∆∆===∴S S S S ，即L K L D G HL G H S S S ∆'∆∆==L D L K '==∴G ,L HL ，是平行四边形四边形GH K D '∴102321KG ==='=∴KD DH H D ……………11分 ③若翻折后，点D '与点K 重合，则重叠部分的面积等于DGK KGH S ∆∆=21S不合题意. ……………12分 综上所述：1023KG 229KG ==或。

开县2014年九年级（上册）英语试卷说明：全卷共九大题，满分150分，120分钟完卷。

本试卷分为试题卷和答题卡，答案写在答题卡上，考试结束后，将答题卡交回。

第Ⅰ卷（共100 分）Ⅰ．听力测试（共30分）第一节：情景反应。

（每小题1.5分，共9分）听一遍，根据你所听到的句子，从A、B、C三个选项中选出最恰当的答语。

( )1.A.It’s a pleasure. B. With pleasure. C. What a mess!( )2.A. Never mind. B. OK, I will. C. Yes, I think so.( )3. A. Twice a year. B. For four years. C. Not yet.( )4..A. No, I wouldn’t. B. It doesn’t matter. C. Of course, I’d love to.( )5.A. No, I don’t like. B. So do I. C. It’s great. I r eally love living there. ( )6. A.I’ve no idea. B. That’s really a problem. C. The larger, the better.第二节：对话理解。

（每小题1.5分，共9分）听一遍，根据你所听到的对话和问题，从A、B、C三个选项中选出正确答案。

( )7. A. One. B. Two. C. None.( )8. A. It’s beautiful. B. It’s polluted. C. It has no living things.( )9. A. He went shopping. B. He went fishing. C. He did some washing.( )10. A. He can search on the Internet.B. He can ask the teachers.C. He can read newspapers and magazines.( )11.A. To plant more trees. B. To use sun energy. C. To put litter in the dustbin. ( )12.A. In Hangzhou. B. In Wenzhou. C. In Suzhou.第三节:长对话理解（每小题1.5分，共6分）听两遍。

2014-2015学年重庆市开县九年级（上）期末化学试卷一、选择题（本题包括16小题，每小题2分，共32分，每小题只有一个选项符合题意）1．（2分）（2014秋•开县期末）下列各组变化中，前者属于物理变化，后者属于化学变化的是（）A．铜生锈，自行车轮胎爆炸B．高粱酿酒，红磷燃烧C．胆矾研碎，酒精燃烧D．食物腐烂，金属导电2．（2分）（2014秋•开县期末）以下表述不正确的是（）A．水银不是银B．铅笔不含铅C．干冰不是冰D．金刚石是最硬的金属3．（2分）（2014秋•开县期末）下列各组物质中前一种是混合物，后一种是化合物的是（）A．稀硫酸，液氧 B．澄清石灰水，二氧化碳C．石灰石，汽水 D．冰水混合物，氧化铁4．（2分）（2010•连江县模拟）如图所示实验操作中正确的是（）A．滴加少量液体B．过滤C．加热液体D．加入固体5．（2分）（2014秋•开县期末）自然界提供给人类的资源是有限的，为了社会的可持续发展，我们应当珍惜和保护各类资源．下列有关保护自然资源的认识错误的是（）A．B．C．D．7．（2分）（2014秋•开县期末）水是人类宝贵的自然资源，下列有关水的认识或观点错误的是（）A．硬水和软水可以用肥皂水加以鉴别B．山泉水洁净清澈，含多种矿物质，提倡直接作为饮用水C．盛开水的热水瓶底常沉积一层水垢，这说明自来水不是纯净物D．洗菜、淘米、洗衣服的水用来浇花、拖地、冲厕所8．（2分）（2014秋•开县期末）某些花岗岩石材中含有放射性元素氡．一种氡原子的质子数为86，中子数为136，这种氡原子核外电子数为（）A．50 B．86 C．136 D．2229．（2分）（2014秋•开县期末）利用化学知识，可以趋利避害．下列说法中错误的是（）A．合理使用化肥和农药有利于保护水资源B．使用燃煤脱硫技术，减少酸雨的产生C．煤气泄露时向室内洒水能避免一氧化碳中毒D．液化石油气罐放置时要离火源一定距离，防止发生爆炸10．（2分）（2014秋•开县期末）一种廉价的新能源﹣甲醚，它完全燃烧时发生如下反应：X+3O22CO2+3H2O，则X（甲醚）的化学式是（）A．CH4O B．C2H4O C．C3H6O2D．C2H6O11．（2分）（2014秋•开县期末）将少量大豆油倒入一个小铁盒中点燃，用坩埚钳把小铁盒放在冰冷的水面上，可观察到火焰立即熄灭，该实验证明，达到灭火的目的方法之一是（）A．隔绝空气 B．降低着火点C．降温至着火点以下 D．清除可燃物12．（2分）（2008•黑龙江）“雪碧“是一种无色的碳酸饮料，将少量“雪碧“滴入紫色石蕊试液中，然后再加热，溶液的颜色变化情况是（）A．先变红后变紫 B．变红后颜色不再改变C．先变无色后变红D．先变蓝后变紫13．（2分）（2014秋•开县期末）茶叶中含有茶氨酸（C7H14O3N2，又称谷氨酰乙胺），它有降低血压、提高记忆力、保护神经细胞、减肥等效果．下列有关它的说法中，正确的是（）A．茶氨酸中含有1个氮分子B．茶氨酸的相对分子质量为174gC．茶氨酸中氧元素的质量分数为12%D．茶氨酸由C、H、O、N四种元素组成14．（2分）（2014秋•开县期末）建立宏观与微观的联系是化学学科特有的思维方式，下列对于宏观现象的微观解释中错误的是（）A．50mL水和50mL酒精混合后体积小于100mL，是因为分子数目减少了B．一氧化碳和二氧化碳化学性质不同，是因为构成它们的分子不同C．水通电分解，是因为水分子被破坏，形成新的分子D．石墨在一定条件下转化为金刚石是化学变化，是因为碳原子的排列方式发生了改变15．（2分）（2014秋•开县期末）下图所示的实验能达到实验目的是（）A．验证质量守恒定律B．测定空气中的氧气含量C．证明CO2密度比空气大D．证明CO2与水反应16．（2分）（2014•日照校级模拟）在一密闭容器中，有甲、乙、丙、丁四种物质，在一定的条件下，充分反应，测得反应前后各物质质量如下表，关于此反应，下列认识正确的是B．参加反应的甲、丙的质量比为1：9C．乙、丁的相对分子质量比一定为10：9D．甲反应后的质量为8g二、填空题（本题包括6小题，每小题3分，共20分）17．（3分）（2014秋•开县期末）请用化学用语回答问题：（1）两个铜原子；（2）五个五氧化二磷分子；（3）三个亚铁离子．18．（3分）（2014秋•开县期末）生活离不开水，净化、软化水的知识在日常生活中有着广泛应用．（1）茶杯内的纱网，可将茶叶与茶水分离，便于饮用，该设计利用的化学原理是．（2）井水中含有较多的钙、镁离子，硬度较大，为降低硬度，生活中可采用的方法是．（3）自来水厂可用二氧化氯（ClO2）消毒杀菌，ClO2中氯元素化合价为．19．（2分）（2014秋•开县期末）如图给出了水分子的分解示意图．你能从中解读出哪些信息？（请写出2条）（1）；（2）．20．（5分）（2014秋•开县期末）写出化学反应方程式并标明（1）（2）反应的基本类型．（1）铁丝燃烧；（）（2）加热高锰酸钾制氧气；（）（3）天然气（CH4）燃烧．21．（3分）（2014秋•开县期末）正确地认识物质间的联系和区别是学好化学的重要方法之一．如图是小朋同学归纳的知识网络图．请根据该图回答：（1）“反应物的量不同，产物不同”．图中能证明这一观点正确性的是：反应（填序号）．（2）碳和一氧化碳是两种不同的物质，但它们的化学性质有许多相似之处，例如：它们都能与反应，请写出碳与其反应的化学方程式（写一个）．22．（4分）（2014秋•开县期末）如图中的①、②是氟元素、钙元素在元素周期表中的信息，A．B．C．D是四种粒子的结构示意图．请回答：（1）氟元素的相对原子质量为，钙元素的原子序数为；（2）A、B、C、D属于同种元素的粒子是（填字母编号，下同）；（3）A粒子的化学性质与B、C、D中哪一种粒子的化学性质相似．三、实验题（本题包括2小题，共11分）23．（6分）（2014秋•开县期末）如图是实验老师在实验室用双氧水和二氧化锰制取氧气的装置图：请回答：（1）写出标号①仪器的名称；（2）该老师制取氧气应选用的发生装置是（填字母编号）；写出该方法制取氧气的化学反应方程式；收集氧气可选用D装置．理由是；如果用E装置收集氧气，则气体应从（填“a”或“b”）进入．（3）上面发生装置还可以用于实验室制取其他气体，请写出制取其中一种气体化学方程式：．24．（5分）（2014秋•开县期末）为了探究三氧化硫能与水发生反应生成具有酸性的物质．甲同学的实验方案是把三氧化硫（SO3）气体通入紫色石蕊试液中，观察溶液的颜色变化，如图A所示．乙同学的方案是取四朵用石蕊试液染成紫色的干燥小花，按图B进行实验，观察小花颜色变化（紫色石蕊遇酸变红色）．请你就甲、乙两同学的实验方案．回答下列有关问题：（1）乙同学按图B进行实验时，Ⅰ中观察到的现象是石蕊小花变红；Ⅲ中观察到的现象是不变色，你认为应得出的结论是；Ⅵ中观察到的现象是，你认为应得到的结论是．（2）通过以上分析，你认为哪个同学的方案更合理，不合理的原因是．四、计算题（本题包括1小题，共7分）25．（7分）（2014秋•开县期末）实验室用氯酸钾和二氧化锰的混合物共3.45克加热制备氧气，充分反应后，称量剩余固体有2.49克．求：（1）氯酸钾中钾、氯、氧三中元素的质量比？（2）充分反应后产生多少克氧气？（3）原混合物中氯酸钾的质量分数？2014-2015学年重庆市开县九年级（上）期末化学试卷参考答案一、选择题（本题包括16小题，每小题2分，共32分，每小题只有一个选项符合题意）1．C 2．D 3．B 4．A 5．D 6．C 7．B 8．B 9．C 10．D 11．C 12．A 13．D 14．A 15．C 16．B二、填空题（本题包括6小题，每小题3分，共20分）17．2Cu5P2O53Fe2+18．过滤加热煮沸+4价19．水分子中氢和氧的原子个数比为2：1水是由氢元素和氧元素组成的 20．3Fe+2O2Fe3O4化合反应2KMnO4K2MnO4+MnO2+O2↑分解反应CH4+2O2CO2+2H2O21．①②O2C+O2CO222．19.0020BCB三、实验题（本题包括2小题，共11分）23．长颈漏斗A2H2O22H2O+O2↑氧气的密度比空气大aZn+H2SO4=ZnSO4+H2↑或CaCO3+2HCl=CaCl2+H2O+CO2↑24．三氧化硫（SO3）气体无酸性石蕊小花变红三氧化硫（SO3）气体和水生成酸乙乙同学进行了多个对比实验，通过观察小花颜色的变化可以说明：紫色石蕊试液变色不是水作用的结果，也不是三氧化硫（SO3）气体作用的结果，而是三氧化硫（SO3）气体溶于水生成的硫酸的作用的结果．四、计算题（本题包括1小题，共7分）25．。

上学期期末考试九 年 级 数 学 试 卷（本卷共五个大题，满分150分，考试时间 120分钟）案，其中只有一个是正确的，请将正确答案的代号填在题后对应的表格中. 1.下列四个数中的无理数是( )A.3.14B.3-C.4-D.722 2.下列计算正确的是( ) A.4624=÷ B.623=⨯ C.4334=- D.532=+3.方程032=-x x 解是 ( )A. 0或3B. 3C.0D.0或3- 4. 抛物线22(3)4y x =-+-的顶点坐标是( )A.(-3, -4)B.(-3, 4)C.(3, -4)D.(-4, 3)5．下列图形中，是轴对称图形但不是中心对称图形的是（ ）6．如图，AB 是圆O 的直径，点D 在AB 的延长线上，射线DC 切圆O 于点C ，若25A =o∠．则D ∠等于 ( )A ．60°B ．50°C ．40°D ．45° 7.用配方法解方程01422=+-x x ，则方程可变为（ ） A.()2122=-x B.31)1(22=-x C.()1122=-x D.()2112=-x 8.已知两圆的半径1r ，2r 分别是方程01072=+-x x 的两根，两圆的圆心距为7，则两圆的位置关系是（ ）题号 一 二 三 四 五 总分 总分人 得分学校_________________ 班级_________________ 姓名________________ 考号____________________________ ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．装．．．．．．．．．．．．．．．．．．．．．．．．．．．．订．．．．．．．．．．．．．．．．．．．．．．．．．线．．．．．．．．．．．．．．．．．． ×××××××××××××××××××××××密封线内不能答题××××××××××××××××××××××××__________________________________________________________________________________________________________________A. 相交B.内切C.外切D.外离9.彩虹暖手器原价每个100元，随着天气变冷，买的人增多，商场经过连续两次加价a %后售价是每个121元，以下列方程正确的是 ( )A. ()121%11002=-a B. ()121%11002=+aC. ()121%211002=-a D.()121110022=-a10.为提倡低碳生活，小凯坚持骑车上学，有一天，小凯开始以正常速度匀速行驶，但行至中途时，自行车出了故障，只好停下来修车，车修好后，因怕耽误上课，他比修车前加快了速度继续匀速行驶，下列行驶路程s 关于时间t 的函数图象中，符合小凯行驶情况的大致图象是（ ）11．如图是由正三角形、正方形及正六边形组成的图案． 按此规律，第16个图案中，正三角形的个数为（ ）A ．82B ．72C ．83D ．7312. 已知函数c bx ax y ++=2的图象如图所示，给出以下结论：①2b ＞ac 4；②abc ＞0；③02=-b a ；④3ca ->；⑤cb a ++39＜0，其中结论正确有( )A. 2个B. 3个C. 4个D.5个题号 1 2 3 4 5 6 7 8 9 10 11 12 答案二、填空题（每小题4分，共24分）请将答案填在题后的横线上. 13.要使2x -在实数范围内有意义，x 应满足的条件是 . 14.已知圆锥的底面半径为3，母线长为5 ，则圆锥的高是 . 15.若1x =是方程220x ax ++=的一个根，则其另一个根为 .16.如图，一个圆心角为90°的扇形，半径OA=3，那么图中阴影部分的面积为 .（结果保留π）17．现有5张正面分别标有数字2-，1-，0，l ，2的同种卡片，将它们背面朝上，洗匀后从中随机抽取一张，记卡片上的数字为a ，则使关于x 的方程22(1)(3)0x a x a a --+-=有实根，且以x 为自变量的函数a ax x y 422+-=的顶点落在第一象限的概率是________． 18.如图，矩形ABCO 的边OC OA ,分别落在x 、y 轴上，点B 的坐标为B （320，5），D 是BC 边上一点．将COD ∆沿直线OD 翻折，使C 点恰好落在对角线OB 上的点E 处，若点E 在一反比例函数的图象上，则该函数的解析式是 ． 19.计算：()().16323121020142⨯-+---+⎪⎭⎫ ⎝⎛--π20.如图，方格中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，ABC ∆的顶点均在格点上，点C 的坐标为(41)-，．①把ABC ∆向左平移6个单位得到对应的111A B C ∆，画出111A B C ∆，并写出1C 的坐标；②将111C B A ∆绕点O 顺时针旋转90°得到对应的222C B A ∆.写出点2C 的坐标.四、解答题(每小题10分,共40分）每小题必须给出必要的演算过程或推理步骤．21．先化简，再求值：1211222+-+÷⎪⎪⎭⎫ ⎝⎛---+x x x x x x x x ，其中x 为方程0822=--x x 的根.22.某商场将进货价为150元的中学生冬季运动服以200元售出时，平均每周能售出80件，调查表明：这种中学生冬季运动服的售价每上涨1元，其销售量就减少1件.(1)为了使平均每周有4200元的销售利润，这种运动服的售价应定为多少元？(2)4200元是否为最大利润？若是，请说出理由；若不是,求出最大利润,并指出此时运动服的售价为多少元？23.有传言说“明年中考体育将增加男生1000米女生800米为考查选项”，但市教委明确说,明年我市暂不实行.某中学初三数学兴趣小组随机抽查了若干名学生对“中考体育增加男生1000米女生800米”的态度：A. 反对；B.基本赞成；C.赞成；D. 无所谓，并将调查结果绘制成频数折线统计图1和不完整的扇形统计图2．请根据图中信息，解答下列问题：(1) 此次抽样调查中，共调查了多少名学生；(2) 求出图2中扇形C所对的圆心角的度数，并将图1补充完整；(3) 根据抽样调查结果，请你估计该校3000名学生中有多少名学生持反对态度；(4) 此次调查活动中，初三（1）班和（2）班各有2名学生对“中考体育增加男生1000米女生800米”持赞成态度，现从中选2名学生参加区冬运会，试用列表法或画树状图法求所选出的2人来自不同班级的概率.图1 图2DC=，24．如图，H是边长为4的正方形ABCD边AB上一点，N在DH上，且DN DHAG=．MN⊥交BC于点M，G点在BA延长线上，CM（1）求证：CDH ADH HDG ∠+∠=∠21； （2）若2=MN ，求DH 的长．五、解答题(每小题12分,共24分）每小题必须给出必要的演算过程或推理步骤. 25.如图，抛物线c bx x y ++-=22过A （2,0）、C （0，4）两点. （1）分别求该抛物线和直线AC 的解析式;（2）横坐标为m 的点P 是直线AC 上方的抛物线上一动点，△APC 的面积为S . ①求S 与m 的函数关系式;②S 是否有最大值？若存在，求出最大值，若不存在，请说明理由.（3）点M 是直线AC 上一动点，ME 垂直x 轴于E ，在y 轴（原点除外）上是否存在点F ，使MEF ∆为等腰直角三角形? 若存在,求出对应的点M F ,的坐标；若不存在，说明理由.26.如图1，菱形OABC 的边OA 在x 轴正半轴上，已知10=OA ，点)8,6(C ，动点P 从O点出发，以1个单位/秒的速度沿线段OA 运动，OA PQ ⊥交折线段CB OC -于Q ，以PQ 为边向右作正方形PQMN ，当P 到达A 点时，运动结束.设点P 的运动时间为t 秒（t >0）. (1)点B 的坐标为 ，t = 时，点N 与A 重合;（2）整个运动过程中，设正方形PQMN 与菱形OABC 重合部分面积为S ，试写出S 与t 之间的函数关系式和相应的自变量t 的取值范围;（3）如图2,在运动过程中,直线OB 将PQMN 分成两部分，问：是否存在t ，使得被分成的两部分中有一部分的面积是菱形面积的51.若存在，求对应的t 值；若不存在，说明理由.九年级数学答案一．选择题：1-5BBAAB,6-10CDCBC11-12AB 二．填空题：13.x ≥2 14. 4 15.2 16.2949-π 17.5218.x y 12=三．解答题19.解：原式=4+1-（2-3）+1×4…………………5分 =7+3…………………7分 20.C 1（-2，-1）C 2（-1,2）……………………2分画对三角形111C B A ……………………2分 画对三角形222C B A ……………………3分21.解：原式=[]121)1)(1(1222+-+÷--+--+x x xx x x x x x x =121)1(2222+-+÷---+x x xx x x x x=()1)1(112+-⨯-+x x x x x ……………………5分 =xx 1-……………………6分 0822=--x x解得：x 1=-2, x 2=4……………………8分当x=-2时，原式=x x 1-=23212=--- 当x=4时，原式=x x 1-=43414=-所以原式的值是23或43……………………8分 22.解（1）设这种中学生运动服的售价定为x 元，根据题意得： （x-150）[])200(80--x =4200……………………5分 解得：x 1=220，x 2=210答：这种中学生冬季运动服的售价定为220元或210元，平均每周有4200元的销售利润。

2015九年级（上）期末数学试卷一、选择题：（本大题共10小题，每小题3分，共30分，在每小题给出四个选项中，只有一项是符合题目要求的，请把每小题的答案填题后的在括号中）1．下列各组二次根式中是同类二次根式的是（）A．B．C．D．2．下列运算正确的是（）A．3﹣2=1 B．=C．2=2D．÷3=3．关于x的一元二次方程（m﹣2）x2+x+m2﹣4=0有一个根为0，则m的值应为（）A．2 B．﹣2 C．2或﹣2 D． 14．若关于x的一元二次方程mx2﹣2x+1=0无实数根，则一次函数y=（m﹣1）x﹣m图象不经过（）A．第一象限B．第二象限C．第三象限D．第四象限5．在下列四个图案中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．6．已知线段AB=7cm，现以点A为圆心，2cm为半径画⊙A；再以点B为圆心，3cm为半径画⊙B，则⊙A和⊙B的位置关系（）A．内含B．相交C．外切D．外离7．如图，△ABC中，∠B=90°，∠C=30°，AB=1，将△ABC绕顶点A旋转180°，点C落在C′处，则CC′的长为（）A．4B． 4 C．2D．28．如图，AB是半圆O的直径，∠BAC=60°，D是半圆上任意一点，那么∠D的度数是（）A．30° B．45° C．60° D．90°9．下列事件属于随机事件的有（）①当室外温度低于﹣10℃时，将一碗清水放在室外会结冰；②经过城市中某有交通信号灯的路口，遇到红灯；③今年春节会下雪；④5，4，9的三根木条组成三角形．A．② B．②④ C．②③ D．①④10．在拼图游戏中，从图1的四张纸片中，任取两张纸片，能拼成“小房子”（如图2）的概率等于（）A．B．C．D．二、填空题（本大题共8小题，每小题3分，共24分）11．使有意义，则x的取值范围是．12．一个正多边形，它的一个外角等于与它相邻内角的，则这个多边形是．13．已知代数式x2﹣4x﹣2的值为3，则代数式2x2﹣8x﹣5的值为．14．直径分别为4和8的两圆相切，那么两圆的圆心距为．15．如图，把△ABC绕点C顺时针旋转25°，得到△A′B′C，A′B′交AC于点D，若∠A′DC=90°，则∠A=．16．如图，随机闭合开关S1，S2，S3中的两个，能够让灯泡发光的概率为．17．用一张半径为24cm的扇形纸片做一个如图所示的圆锥形小丑帽子侧面（接缝忽略不计），如果做成的圆锥形小丑帽子的底面半径为10cm，那么这张扇形纸片的面积是cm2．18．一个口袋里有25个球，其中红球、黑球、黄球若干个，从口袋中随机摸出一球记下其颜色，再把它放回口袋中摇匀，重复上述过程，共试验200次，其中有120次摸到黄球，由此估计袋中的黄球有个．三.解答题（本大题共8小题，共66分，解答应写出文字说明，演算步骤或证明过程）19．计算（1）；（2）．20．解下列方程（1）x2+2x﹣3=0（2）x（2x﹣5）=2x﹣5．21．如图，利用关于原点对称的点的坐标特点，画出△ABC关于原点O对称的△A1B1C1，并写出点A1、B1、C1的坐标．22．已知电流在一定时间内正常通过电子元件的概率为0.5，分别求在一定时间内A、B之间电流通过的概率．（要求：解答分两步：第一步用列举法写出各种可能的结果；第二步，求A、B之间电流通过的概率．）23．如图，⊙O是△ABC的外接圆，AB是⊙O的直径，D为⊙O上一点，OD⊥AC，垂足为E，连接BD．（1）求证：BD平分∠ABC；（2）当∠ODB=30°，BC=，求⊙O的半径．24．如图，某中学准备在校园里利用围墙的一段，再砌三面墙，围成一个矩形花园ABCD （围墙MN最长可利用25m），现在已备足可以砌50m长的墙的材料，试设计一种砌法，使矩形花园的面积为300m2．25．在4张完全相同的卡片正面分别写上数字1，2，3，3，现将它们的背面朝上洗均匀．（1）随机抽出一张卡片，求抽到数字“3”的概率；（2）若随机抽出一张卡片记下数字后放回并洗均匀，再随机抽出一张卡片，求两次都是抽到数字“3”的概率；（要求画树状图或列表求解）（3）如果再增加若干张写有数字“3”的同样卡片，洗均匀后，使得随机抽出一张卡片是数字“3”的概率为，问增加了多少张卡片？26．如图，点P在y轴上，⊙P交x轴于A、B两点，连结BP并延长交⊙P于C，过点C 的直线y=2x+b交x轴于D，且⊙P的半径为，AB=4．（1）求点B、P、C的坐标；（2）求证：CD是⊙P的切线．参考答案与试题解析一、选择题：（本大题共10小题，每小题3分，共30分，在每小题给出四个选项中，只有一项是符合题目要求的，请把每小题的答案填题后的在括号中）1．下列各组二次根式中是同类二次根式的是（）A．B．C．D．考点：同类二次根式．分析：化简各选项后根据同类二次根式的定义判断．解答：解：A、=2与被开方数不同，故不是同类二次根式，故A选项错误；B、与被开方数不同，故不是同类二次根式，故B选项错误；C、与被开方数相同，是同类二次根式，故C选项正确；D、与被开方数不同，故不是同类二次根式，故D选项错误．故选：C．点评：本题考查了同类二次根式的定义：化成最简二次根式后，被开方数相同，这样的二次根式叫做同类二次根式．2．下列运算正确的是（）A．3﹣2=1 B．=C．2=2D．÷3=考点：二次根式的混合运算．专题：计算题．分析：根据合并同类二次根式对A、B进行判断；根据二次根式的乘法法则对C进行判断；根据二次根式的除法对D进行判断．解答：解：A、3﹣2=，所以A选项错误；B、与不能合并，所以B选项错误；C、2×2=4，所以C选项错误；D、÷3=3÷3=，所以D选项正确．故选D．点评：本题考查了二次根式的混合运算：先把各二次根式化为最简二次根式，在进行二次根式的乘除运算，然后合并同类二次根式．3．关于x的一元二次方程（m﹣2）x2+x+m2﹣4=0有一个根为0，则m的值应为（）A．2 B．﹣2 C．2或﹣2 D． 1考点：一元二次方程的解；一元二次方程的定义．分析：把x=0代入已知方程，列出关于m的新方程，通过解新方程可以求得m的值．解答：解：∵关于x的一元二次方程（m﹣2）x2+x+m2﹣4=0有一个根为0，∴m2﹣4=0且m﹣2≠0，解得，m=﹣2．故选：B．点评：本题考查了一元二次方程的解的定义和一元二次方程的定义．解题时，注意一元二次方程的二次项系数一定不能等于零．4．若关于x的一元二次方程mx2﹣2x+1=0无实数根，则一次函数y=（m﹣1）x﹣m图象不经过（）A．第一象限B．第二象限C．第三象限D．第四象限考点：根的判别式；一次函数图象与系数的关系．专题：计算题．分析：根据判别式的意义得到m≠0且△=（﹣2）2﹣4m＜0，解得m＞1，然后根据一次函数的性质可得到一次函数y=（m﹣1）x﹣m图象经过第一、三象限，且与y轴的交点在x 轴下方．解答：解：根据题意得m≠0且△=（﹣2）2﹣4m＜0，解得m＞1，∵m﹣1＞0，﹣m＜0，∴一次函数y=（m﹣1）x﹣m图象经过第一、三、四象限．故选B．点评：本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2﹣4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．也考查了一次函数图象与系数的关系．5．在下列四个图案中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．考点：中心对称图形；轴对称图形．分析：根据轴对称图形与中心对称图形的概念求解．解答：解：A、既是轴对称图形，又是中心对称图形，故本选项正确；B、是轴对称图形，不是中心对称图形，故本选项错误；C、不是轴对称图形，是中心对称图形，故本选项错误；D、既是轴对称图形，不是中心对称图形，故本选项错误．故选A．点评：本题考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．6．已知线段AB=7cm，现以点A为圆心，2cm为半径画⊙A；再以点B为圆心，3cm为半径画⊙B，则⊙A和⊙B的位置关系（）A．内含B．相交C．外切D．外离考点：圆与圆的位置关系．分析：针对两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系得出两圆位置关系．解答：解：依题意，线段AB=7cm，现以点A为圆心，2cm为半径画⊙A；再以点B为圆心，3cm为半径画⊙B，∴R+r=3+2=5，d=7，所以两圆外离．故选D．点评：此题主要考查了圆与圆的位置关系，圆与圆的位置关系与数量关系间的联系．此类题为中考热点，需重点掌握．7．如图，△ABC中，∠B=90°，∠C=30°，AB=1，将△ABC绕顶点A旋转180°，点C落在C′处，则CC′的长为（）A．4B． 4 C．2D．2考点：解直角三角形；旋转的性质．专题：计算题．分析：因为在△ABC中，∠B=90°，∠C=30°，AB=1，由此得到AC=2，又根据旋转可以推出AC′=AC，即可求出CC′．解答：解：∵在△ABC中，∠B=90°，∠C=30°，AB=1，∴AC=2．∵将△ABC绕顶点A旋转180°，点C落在C′处，AC′=AC=2，∴CC′=4．故选B．点评：此题主要考查学生对旋转的性质及综合解直角三角形的运用能力．8．如图，AB是半圆O的直径，∠BAC=60°，D是半圆上任意一点，那么∠D的度数是（）A．30° B．45° C．60° D．90°考点：圆周角定理；等边三角形的判定与性质．分析：首先连接BC，由AB是半圆的直径，根据直径所对的圆周角是直角即可求得∠D的度数．解答：解：连接BC，∵AB是半圆的直径∴∠ACB=90°∵∠BAC=60°，∴∠ABC=90°﹣∠BAC=30°，∴∠D=∠ABC=30°．故选A．点评：本题题考查了圆周角定理此题比较简单，注意掌握辅助线的作法，注意数形结合思想的应用．9．下列事件属于随机事件的有（）①当室外温度低于﹣10℃时，将一碗清水放在室外会结冰；②经过城市中某有交通信号灯的路口，遇到红灯；③今年春节会下雪；④5，4，9的三根木条组成三角形．A．② B．②④ C．②③ D．①④考点：随机事件．分析：根据不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件，对各小题分析判断即可得解．解答：解：①当室外温度低于﹣10℃时，将一碗清水放在室外会结冰，是必然事件；②经过城市中某有交通信号灯的路口，遇到红灯，是随机事件；③今年春节会下雪，是随机事件；④5，4，9的三根木条组成三角形，是不可能事件，所以，属于随机事件的是②③．故选C．点评：本题考查了随机事件，关键在于正确理解必然事件、不可能事件、随机事件的概念．用到的知识点为：确定事件包括必然事件和不可能事件．必然事件指在一定条件下一定发生的事件不可能事件是指在一定条件下，一定不发生的事件．不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．10．在拼图游戏中，从图1的四张纸片中，任取两张纸片，能拼成“小房子”（如图2）的概率等于（）A．B．C．D．考点：列表法与树状图法．分析：先用列举法求出两张纸片的所有组合情况，再根据概率公式解答．解答：解：任取两张纸片，能拼成“小房子”（如图2）的概率等于，即．故选D．点评：用到的知识点为：概率=所求情况数与总情况数之比．二、填空题（本大题共8小题，每小题3分，共24分）11．使有意义，则x的取值范围是x≥﹣且x≠0．考点：二次根式有意义的条件；分式有意义的条件．分析：根据被开方数大于等于0，分母不等于0列式求解即可．解答：解：根据题意得，3x+2≥0且x≠0，解得x≥﹣且x≠0．故答案为：x≥﹣且x≠0．点评：本题考查的知识点为：分式有意义，分母不为0；二次根式的被开方数是非负数．12．一个正多边形，它的一个外角等于与它相邻内角的，则这个多边形是正十边形．考点：多边形内角与外角．专题：应用题．分析：外角等于与它不相邻的内角的四分之一可知该多边形内角为144°，外角36°，根据正多边形外角和=360°，利用360÷36即可解决问题．解答：解：∵一个正多边形它的一个外角等于与它相邻的内角的，∴它的每一个外角=180÷5=36°，∴它的边数=360÷36=10．故答案为正十边形．点评：本题主要考查了多边形的外角和等于360度，难度适中．13．已知代数式x2﹣4x﹣2的值为3，则代数式2x2﹣8x﹣5的值为5．考点：代数式求值．专题：计算题．分析：根据题意求出x2﹣4x的值，原式前两项提取2变形后，将x2﹣4x的值代入计算即可求出值．解答：解：∵x2﹣4x﹣2=3，即x2﹣4x=5，∴原式=2（x2﹣4x）﹣5=10﹣5=5．故答案为：5．点评：此题考查了代数式求值，利用了整体代入的思想，熟练掌握运算法则是解本题的关键．14．直径分别为4和8的两圆相切，那么两圆的圆心距为2或6．考点：圆与圆的位置关系．分析：两圆相切，则两圆外切或内切．当两圆外切时，圆心距等于两圆半径之和；当两圆内切时，圆心距等于两圆半径之差．解答：解：当两圆外切时，则圆心距等于4÷2+8÷2=6；当两圆内切时，则圆心距等于8÷2﹣4÷2=2．故答案为：2或6．点评：此题考查了两圆的位置关系与数量之间的联系．注意：两圆相切，则两圆内切或外切．15．如图，把△ABC绕点C顺时针旋转25°，得到△A′B′C，A′B′交AC于点D，若∠A′DC=90°，则∠A=65°．考点：旋转的性质．专题：计算题．分析：根据旋转的性质对应点与旋转中心的连线段的夹角等于旋转角得到∠ACA′=25°，而∠A′DC=90°，则∠A′=90°﹣25°=65°，然后再根据旋转的性质即可得到∠A=65°．解答：解：∵△ABC绕点C顺时针旋转25°，得到△A′B′C，∴∠ACA′=25°，又∵∠A′DC=90°，∴∠A′=90°﹣25°=65°，∴∠A=65°．故答案为65°．点评：本题考查了旋转的性质：旋转前后两图形全等，即对应角相等，对应边相等，对应点与旋转中心的连线段的夹角等于旋转角．16．如图，随机闭合开关S1，S2，S3中的两个，能够让灯泡发光的概率为．考点：概率公式．专题：跨学科．分析：根据题意可得：随机闭合开关S1，S2，S3中的两个，有3种方法，其中有两种能够让灯泡发光，故其概率为．解答：解：P（灯泡发光）=．故本题答案为：．点评：本题考查的是概率的求法．如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．17．用一张半径为24cm的扇形纸片做一个如图所示的圆锥形小丑帽子侧面（接缝忽略不计），如果做成的圆锥形小丑帽子的底面半径为10cm，那么这张扇形纸片的面积是240πcm2．考点：圆锥的计算．专题：压轴题；数形结合．分析：易得圆锥的底面周长，利用侧面积公式可得扇形纸片的面积．解答：解：∵圆锥的底面周长为20π，∴扇形纸片的面积=×20π×24=240πcm2．故答案为240π．点评：考查圆锥的计算，用到的知识点为：圆锥的底面周长=侧面展开图的弧长；圆锥的侧面积=LR．18．一个口袋里有25个球，其中红球、黑球、黄球若干个，从口袋中随机摸出一球记下其颜色，再把它放回口袋中摇匀，重复上述过程，共试验200次，其中有120次摸到黄球，由此估计袋中的黄球有15个．考点：利用频率估计概率．分析：先求出试验200次摸到黄球的频率，再乘以总球的个数即可．解答：解：∵口袋里有25个球，试验200次，其中有120次摸到黄球，∴摸到黄球的频率为：=，∴袋中的黄球有25×=15个．故估计袋中的黄球有15个．点评：用到的知识点为：部分的具体数目=总体数目×相应频率．三.解答题（本大题共8小题，共66分，解答应写出文字说明，演算步骤或证明过程）19．计算（1）；（2）．考点：二次根式的混合运算．专题：计算题．分析：（1）先把各二次根式化为最简二次根式，然后合并即可；（2）根二次根式的乘除法则进行计算．解答：解：（1）原式=2+﹣2=；（2）原式=2×××=．点评：本题考查了二次根式的混合运算：先把各二次根式化为最简二次根式，在进行二次根式的乘除运算，然后合并同类二次根式．20．解下列方程（1）x2+2x﹣3=0（2）x（2x﹣5）=2x﹣5．考点：解一元二次方程-因式分解法．专题：计算题．分析：（1）利用因式分解法解方程；（2）先移项得到x（2x﹣5）﹣（2x﹣5）=0，再利用因式分解法解方程．解答：解：（1）（x﹣1）（x+3）=0，x﹣1=0或x+3=0，所以x1=1，x2=﹣3；（2）x（2x﹣5）﹣（2x﹣5）=0，（2x﹣5）（x﹣1）=0，2x﹣5=0或x﹣1=0，所以x1=，x2=1．点评：本题考查了解一元二次方程﹣因式分解法：先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．21．如图，利用关于原点对称的点的坐标特点，画出△ABC关于原点O对称的△A1B1C1，并写出点A1、B1、C1的坐标．考点：作图-旋转变换．专题：作图题．分析：根据平面直角坐标系找出点A、B、C关于原点对称的A1、B1、C1的位置，然后顺次连接即可，再根据关于原点对称的点的横坐标与纵坐标写出A1、B1、C1的坐标．解答：解：△A1B1C1如图所示；A1（3，﹣2），B1（2，1），C1（﹣2，﹣3）．点评：本题考查了利用旋转变换作图，根据平面直角坐标系准确找出对应点的位置是解题的关键．22．已知电流在一定时间内正常通过电子元件的概率为0.5，分别求在一定时间内A、B之间电流通过的概率．（要求：解答分两步：第一步用列举法写出各种可能的结果；第二步，求A、B之间电流通过的概率．）考点：列表法与树状图法．专题：计算题．分析：画树状图得出所有等可能的情况数，找出通电的情况，即可求出所求概率．解答：解：画树状图，如图所示：，得出所有等可能的情况有4种，其中通电的占3种，则P（通电）=．点评：此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．23．如图，⊙O是△ABC的外接圆，AB是⊙O的直径，D为⊙O上一点，OD⊥AC，垂足为E，连接BD．（1）求证：BD平分∠ABC；（2）当∠ODB=30°，BC=，求⊙O的半径．考点：圆周角定理；勾股定理；垂径定理．专题：证明题．分析：（1）根据垂径定理得到弧CD=弧AD，然后根据圆周角定理得∠CBD=∠DBA；（2）由于∠OBD=∠ODB=30°，则∠ABC=60°，再根据半圆（或直径）所对的圆周角是直角得到∠ACB=90°，然后根据含30度的直角三角形三边的关系．可得到直径AB的长，则即可得到圆的半径．解答：（1）证明：∵OD⊥AC，∴弧CD=弧AD，∴∠CBD=∠DBA，∴BD平分∠ABC；（2）解：∵OD=OB，∴∠OBD=∠ODB=30°，∴∠ABC=60°，∵AB是⊙O的直径，∴∠ACB=90°，在Rt△ABC中，∠A=30°，BC=，∴AB=2BC=2，∴⊙O的半径为．点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．也考查了垂径定理和含30度的直角三角形三边的关系．24．如图，某中学准备在校园里利用围墙的一段，再砌三面墙，围成一个矩形花园ABCD （围墙MN最长可利用25m），现在已备足可以砌50m长的墙的材料，试设计一种砌法，使矩形花园的面积为300m2．考点：一元二次方程的应用．分析：根据可以砌50m长的墙的材料，即总长度是50米，AB=x米，则BC=（50﹣2x）米，再根据矩形的面积公式列方程，解一元二次方程即可．解答：解：设AB=x米，则BC=（50﹣2x）米．根据题意可得，x（50﹣2x）=300，解得：x1=10，x2=15，当x=10，BC=50﹣10﹣10=30＞25，故x1=10（不合题意舍去），当x=15时，BC=50﹣2×15=20（米）．答：可以围成AB的长为15米，BC为20米的矩形．点评：本题考查了一元二次方程的应用．解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系求解，注意围墙MN最长可利用25m，舍掉不符合题意的数据．25．在4张完全相同的卡片正面分别写上数字1，2，3，3，现将它们的背面朝上洗均匀．（1）随机抽出一张卡片，求抽到数字“3”的概率；（2）若随机抽出一张卡片记下数字后放回并洗均匀，再随机抽出一张卡片，求两次都是抽到数字“3”的概率；（要求画树状图或列表求解）（3）如果再增加若干张写有数字“3”的同样卡片，洗均匀后，使得随机抽出一张卡片是数字“3”的概率为，问增加了多少张卡片？考点：列表法与树状图法；概率公式．分析：（1）由有4张完全相同的卡片正面分别写上数字1，2，3，3，抽到数字“3”的有2种情况，利用概率公式求解即可求得答案；（2）首先根据题意列出表格，然后由表格求得所有等可能的结果与两次都是抽到数字“3”的情况，再利用概率公式求解即可求得答案；（3）首先设增加了x张卡片，即可得方程：=，解此方程即可求得答案．解答：解：（1）∵有4张完全相同的卡片正面分别写上数字1，2，3，3，抽到数字“3”的有2种情况，∴随机抽出一张卡片，抽到数字“3”的概率为：=；（2）列表得：第二张第一张1 2 3 31 （1，1）（1，2）（1，3）（1，3）2 （2，1）（2，2）（2，3）（2，3）3 （3，1）（3，2）（3，3）（3，3）3 （3，1）（3，2）（3，3）（3，3）∵共有16种等可能的结果，两次都是抽到数字“3”的有4种情况，∴P（两次都是抽到数字“3”）==；（3）设增加了x张卡片，则有：=，解得：x=4，∴增加了4张卡片．点评：此题考查的是用列表法或树状图法求概率．注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；注意概率=所求情况数与总情况数之比．26．如图，点P在y轴上，⊙P交x轴于A、B两点，连结BP并延长交⊙P于C，过点C 的直线y=2x+b交x轴于D，且⊙P的半径为，AB=4．（1）求点B、P、C的坐标；（2）求证：CD是⊙P的切线．考点：切线的判定；一次函数图象上点的坐标特征；全等三角形的判定与性质．分析：（1）连结AC，由于BC是圆P的直径，那么∠CAB=90°．解Rt△ABC，得出AC==2，由垂径定理得出OB=OA=2，根据三角形中位线定理得出OP=AC=1，从而求出点B、P、C的坐标；（2）将C（﹣2，2）代入y=2x+b，利用待定系数法求出过点C的直线解析式为y=2x+6，得到D（﹣3，0），AD=1．再利用SAS证明△ADC≌△OPB，得出∠DCA=∠B，然后证明∠BCD=90°，根据切线的判定定理证明CD是⊙P的切线．解答：（1）解：连结AC．∵BC是⊙P的直径，∴∠CAB=90°．在Rt△ABC中，∵∠CAB=90°，BC=2，AB=4，∴AC==2，∵OP⊥AB，∴OB=OA=2，∴OP=AC=1，∴P（0，1），B（2，0），C（﹣2，2）；（2）证明：将C（﹣2，2）代入y=2x+b，得﹣4+b=2，解得b=6∴y=2x+6，当y=0时，则x=﹣3，∴D（﹣3，0），∴AD=1．在△ADC和△OPB中，，∴△ADC≌△OPB（SAS），∴∠DCA=∠B．∵∠B+∠ACB=90°，∴∠DCA+∠ACB=90°，即∠BCD=90°，∴CD是⊙P的切线．点评：本题考查了切线的判定，垂径定理，勾股定理，全等三角形的判定与性质等知识点．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．。