2019年广西梧州市高考数学一模试卷(理科)〖详解版〗

高考满分作文经验分享同学们在进入高三之前，一定要调整自己的状态，为总复习提前打好基础。

那么如何才能做到这一点呢？又该如何准备呢？俗话说“题好一半文”，一个好的题目是可以为作文加分的。

现在的考试作文，多是不命题作文，所以就很考验题目“抓眼球”的程度。

当然，前提是你的题目得扣题，不偏题，如果你没有把握，那就按照最普通的方法去拟题。

从近年来的高分甚至满分作文中，我们不难发现，这些作文都有一个比较吸引人的标题。

其中能找到的规律是：对偶逗号式、经典句子换用式、诗词化用式、俗语改动式、固定搭配转换式。

一般三段式的文章会导致中间一段过长，使人看不到重点，分不清条理。

而段落过多的话会显得繁琐。

除了拒绝“大肚子”似的三段式作文外，开头结尾一定要简洁，特别是开头，如果占有太多空间，会入题过慢，引起阅卷疲劳。

一般高分作文在用词和语句上都不会太平淡，会使用大量丰富的词汇和富有诗意的句子，而这些就需要我们注意积累了。

平时，不管是在书本上，还是网络上看到的比较好的句子，都可以摘抄下来，等量积累到一定程度，自己写作也就信手拈来了。

多用哲理化、诗意化的句子表达，但切忌浮夸的词藻堆砌，让人不知所云。

一些高分文章往往都能够引经据典，素材十分丰富。

考生们在拿到一个题目后，短时间内能调用各种相关的人物、事例来论证，从古至今，从经典到时下热点......所以，平时多读书，多积累案例素材，也要学会活用课本知识，不需要刻意去背相关的段落，只需要记住相关的人物的具体事件或生平，具体语言用自己的风格来表述即可。

但不要用一些李白、屈原这种烂大街的例子，避免写出来文章千篇一律。

议论文切忌论点不明确，一定要用合理的案例来支撑一个观点，不要模棱两可，表示两个方向都是对的。

前面虽然提到词汇量要丰富，但要在文章有自己的思想和创造性的前提下。

要不然词语再华丽也是空洞的。

如果想要培养自己的写作素养，大家可以多看看《人民日报》等主流媒体的评论文章，可以学到一些思考方向。

广西省梧州市2019-2020学年高考数学一模考试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知数列{}n a 的前n 项和为n S ，且14121n n S a n +-=-，11a =，*n N ∈，则{}n a 的通项公式n a =（ ） A ．nB ．1n +C ．21n -D ．21n + 【答案】C【解析】【分析】利用()12n n n a S S n -=-≥证得数列21n a n ⎧⎫⎨⎬-⎩⎭为常数列，并由此求得{}n a 的通项公式. 【详解】 由14121n n S a n +-=-，得1(21)41n n n a S +-=-，可得1(23)41n n n a S --=-（2n ≥）. 相减得1(21)(21)n n n a n a ++=-，则12121n n a a n n +=-+（2n ≥），又 由14121n n S a n +-=-，11a =，得23a =，所以12211211a a =⨯-⨯+，所以21n a n ⎧⎫⎨⎬-⎩⎭为常 数列，所以1121211n a a n ==-⨯-，故21n a n =-. 故选：C【点睛】本小题考查数列的通项与前n 项和的关系等基础知识；考查运算求解能力，逻辑推理能力，应用意识.2．若双曲线()22210x y a a-=>的一条渐近线与圆()2222x y +-=至多有一个交点，则双曲线的离心率的取值范围是（ ）A ．)+∞B ．[)2,+∞C ．(D ．(]1,2 【答案】C【解析】【分析】求得双曲线的渐近线方程，可得圆心()0,2到渐近线的距离d ≥，由点到直线的距离公式可得a 的范围，再由离心率公式计算即可得到所求范围．【详解】 双曲线()22210x y a a-=>的一条渐近线为1y x a =，即0x ay -=，由题意知，直线0x ay -=与圆()2222x y +-=相切或相离，则d =≥，解得1a ≥，因此，双曲线的离心率(c e a ==. 故选：C.【点睛】本题考查双曲线的离心率的范围，注意运用圆心到渐近线的距离不小于半径，考查化简整理的运算能力，属于中档题．3．已知向量a r 与向量()4,6m =u r 平行，()5,1b =-r ，且14a b ⋅=r r ，则a =r （ ）A ．()4,6B ．()4,6--C ．1313⎛ ⎝⎭D ．⎛ ⎝⎭【答案】B【解析】【分析】 设(),a x y =r ，根据题意得出关于x 、y 的方程组，解出这两个未知数的值，即可得出向量a r 的坐标.【详解】设(),a x y =r ，且()4,6m =u r ，()5,1b =-r ，由//a m r u r 得64x y =，即32x y =，①，由514a b x y ⋅=-+=r r ，②，所以32514x y x y =⎧⎨-+=⎩，解得46x y =-⎧⎨=-⎩，因此，()4,6a =--r . 故选：B.【点睛】本题考查向量坐标的求解，涉及共线向量的坐标表示和向量数量积的坐标运算，考查计算能力，属于中等题.4．若不等式22ln x x x ax -+…对[1,)x ∈+∞恒成立，则实数a 的取值范围是（ ）A ．(,0)-∞B ．(,1]-∞C ．(0,)+∞D ．[1,)+∞【答案】B【解析】【分析】转化22ln ,[1,)x x x ax x -+∈+∞…为2ln a x x +…，构造函数()2ln ,[1,)h x x x x =+∈+∞，利用导数研究单调性，求函数最值，即得解.【详解】由22ln ,[1,)x x x ax x -+∈+∞…，可知2ln a x x +…．设()2ln ,[1,)h x x x x =+∈+∞，则2()10hx x'=+>， 所以函数()h x 在[1,)+∞上单调递增，所以min ()(1)1h x h ==．所以min ()1a h x =…． 故a 的取值范围是(,1]-∞．故选：B【点睛】 本题考查了导数在恒成立问题中的应用，考查了学生综合分析，转化划归，数学运算的能力，属于中档题.5．设不等式组030x y x y +≥⎧⎪⎨-≤⎪⎩表示的平面区域为Ω，若从圆C ：224x y +=的内部随机选取一点P ，则P 取自Ω的概率为（ ）A ．524B ．724C ．1124D ．1724【答案】B【解析】【分析】画出不等式组表示的可行域，求得阴影部分扇形对应的圆心角，根据几何概型概率计算公式，计算出所求概率.【详解】作出Ω中在圆C 内部的区域，如图所示，因为直线0x y +=，30x -=的倾斜角分别为34π，6π， 所以由图可得P 取自Ω的概率为3746224πππ-=.故选：B【点睛】本小题主要考查几何概型的计算，考查线性可行域的画法，属于基础题.6．已知函数()sin(2019)cos(2019)44f x x x ππ=++-的最大值为M ，若存在实数,m n ，使得对任意实数x 总有()()()f m f x f n ≤≤成立，则M m n ⋅-的最小值为（ ）A ．2019πB ．22019πC ．42019πD ．4038π【答案】B【解析】【分析】根据三角函数的两角和差公式得到()f x =2sin(2019)4x π+，进而可以得到函数的最值，区间(m,n)长度要大于等于半个周期，最终得到结果.【详解】函数()sin 2019cos 201944f x x x ππ⎛⎫⎛⎫=++-= ⎪ ⎪⎝⎭⎝⎭)sin 2019cos 2019cos 2019sin 20192x x x x +++ )sin 2019cos 20192sin(2019)4x x x π=+=+则函数的最大值为2，2M m n m n ⋅-=-存在实数,m n ，使得对任意实数x 总有()()()f m f x f n ≤≤成立，则区间(m,n)长度要大于等于半个周期，即min 2220192019m n m n ππ-≥∴-= 故答案为：B.【点睛】这个题目考查了三角函数的两角和差的正余弦公式的应用，以及三角函数的图像的性质的应用，题目比较综合.7．如图，在三棱柱111ABC A B C -中，底面为正三角形，侧棱垂直底面，148AB AA ==，.若E F ，分别是棱1BB CC ，上的点，且1BE B E =，1114C F CC =，则异面直线1A E 与AF 所成角的余弦值为（ ）A．210B．2613C．1313D．1310【答案】B【解析】【分析】建立空间直角坐标系，利用向量法计算出异面直线1A E与AF所成角的余弦值.【详解】依题意三棱柱底面是正三角形且侧棱垂直于底面.设AB的中点为O，建立空间直角坐标系如下图所示.所以()()()()10,2,8,0,2,4,0,2,0,23,0,6A E A F---，所以()()10,4,4,23,2,6A E AF=-=-u u u r u u u r.所以异面直线1A E与AF所成角的余弦值为118242642213A E AFA E AF⋅-==⨯⋅u u u r u u u ru u u r u u u r.故选：B【点睛】本小题主要考查异面直线所成的角的求法，属于中档题.8．要排出高三某班一天中，语文、数学、英语各2节，自习课1节的功课表，其中上午5节，下午2节，若要求2节语文课必须相邻且2节数学课也必须相邻（注意：上午第五节和下午第一节不算相邻），则不同的排法种数是（）A．84B．54C．42D．18【答案】C【解析】【分析】根据题意，分两种情况进行讨论：①语文和数学都安排在上午；②语文和数学一个安排在上午，一个安排在下午.分别求出每一种情况的安排方法数目，由分类加法计数原理可得答案．【详解】根据题意，分两种情况进行讨论：①语文和数学都安排在上午，要求2节语文课必须相邻且2节数学课也必须相邻，将2节语文课和2节数学课分别捆绑，然后在剩余3节课中选1节到上午，由于2节英语课不加以区分，此时，排法种数为1233232218C A AA=种；②语文和数学都一个安排在上午，一个安排在下午.语文和数学一个安排在上午，一个安排在下午，但2节语文课不加以区分，2节数学课不加以区分，2节英语课也不加以区分，此时，排法种数为14242224C AA=种.综上所述，共有182442+=种不同的排法.故选：C．【点睛】本题考查排列、组合的应用，涉及分类计数原理的应用，属于中等题．9．若函数f(x)＝13x3＋x2－23在区间(a，a＋5)上存在最小值，则实数a的取值范围是A．[－5，0) B．(－5，0) C．[－3，0) D．(－3，0)【答案】C【解析】【分析】求函数导数，分析函数单调性得到函数的简图，得到a满足的不等式组，从而得解.【详解】由题意，f′(x)＝x2＋2x＝x(x＋2)，故f(x)在(－∞，－2)，(0，＋∞)上是增函数，在(－2，0)上是减函数，作出其图象如图所示．令13x 3＋x 2－23＝－23，得x ＝0或x ＝－3， 则结合图象可知，3050a a -≤<⎧⎨+>⎩解得a ∈[－3，0)， 故选C.【点睛】本题主要考查了利用函数导数研究函数的单调性，进而研究函数的最值，属于常考题型.10．命题p ：2(1,2],20()x x x a a ∀∈--+≥∈R 的否定为A ．2000(1,2],20()x x x a a ∃∈--+≥∈RB ．2(1,2],20()x x x a a ∀∈--+<∈RC ．2000(1,2],20()x x x a a ∃∈--+<∈R D ．2(1,2],20()x x x a a ∀∉--+<∈R 【答案】C【解析】【分析】【详解】命题p 为全称命题，它的否定为特称命题，将全称量词改为存在量词，并将结论否定，可知命题p 的否定为2000(1,2],20()x x x a a ∃∈--+<∈R ，故选C ． 11．某几何体的三视图如图所示，三视图是腰长为1的等腰直角三角形和边长为1的正方形，则该几何体中最长的棱长为（ ）．A 2B 3C ．1D 6【答案】B【解析】【分析】 首先由三视图还原几何体，进一步求出几何体的棱长．【详解】解：根据三视图还原几何体如图所示，所以，该四棱锥体的最长的棱长为2221113l =++故选：B ．【点睛】本题主要考查由三视图还原几何体，考查运算能力和推理能力，属于基础题．12．设x ，y 满足约束条件21210x y x y x y +≤⎧⎪+≥-⎨⎪-≤⎩，若32z x y =-+的最大值为n ，则2n x x ⎛ ⎝的展开式中2x 项的系数为( )A ．60B ．80C ．90D ．120【答案】B【解析】【分析】画出可行域和目标函数，根据平移得到5n =，再利用二项式定理计算得到答案.【详解】如图所示：画出可行域和目标函数， 32z x y =-+，即322z y x =+，故z 表示直线与y 截距的2倍， 根据图像知：当1,1x y =-=时，32z x y =-+的最大值为5，故5n =.52x x ⎛ ⎝展开式的通项为：()()35552155221rr r r r r r r T C x C x x ---+⎛=⋅=⋅⋅-⋅ ⎝， 取2r =得到2x 项的系数为：()225252180C -⋅⋅-=. 故选：B .【点睛】本题考查了线性规划求最值，二项式定理，意在考查学生的计算能力和综合应用能力.二、填空题：本题共4小题，每小题5分，共20分。

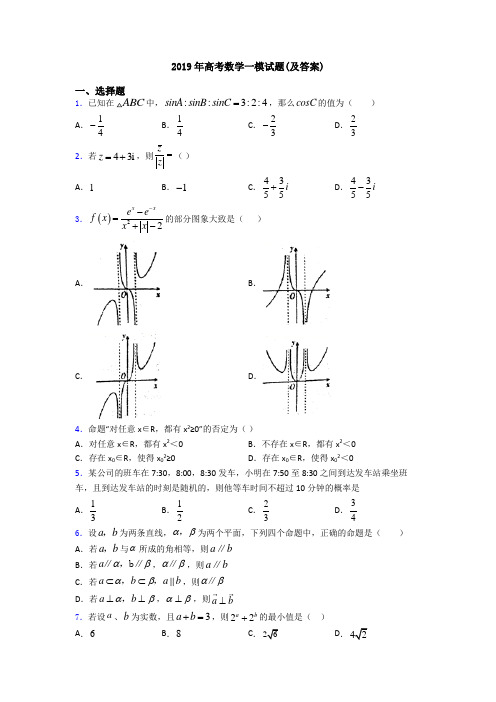
2019年高考数学一模试题(及答案)一、选择题1．已知在ABC 中，::3:2:4sinA sinB sinC =，那么cosC 的值为（ ）A ．14-B ．14C ．23-D ．232．若43i z =+，则zz=（ ） A ．1B ．1-C ．4355i + D ．4355i - 3．()22x xe ef x x x --=+-的部分图象大致是（ ）A ．B ．C ．D ．4．命题“对任意x ∈R ，都有x 2≥0”的否定为（ ） A ．对任意x ∈R ，都有x 2＜0 B ．不存在x ∈R ，都有x 2＜0 C ．存在x 0∈R ，使得x 02≥0D ．存在x 0∈R ，使得x 02＜05．某公司的班车在7:30，8:00，8:30发车，小明在7:50至8:30之间到达发车站乘坐班车，且到达发车站的时刻是随机的，则他等车时间不超过10分钟的概率是A ．13B ．12 C ．23 D ．346．设a b ，为两条直线，αβ，为两个平面，下列四个命题中，正确的命题是（ ） A ．若a b ，与α所成的角相等，则a b ∥B ．若a αβ∥，b ∥，αβ∥，则a b ∥C ．若a b a b αβ⊂⊂，，，则αβ∥D ．若a b αβ⊥⊥，，αβ⊥，则a b ⊥7．若设a 、b 为实数，且3a b +=，则22a b +的最小值是（ ） A ．6B ．8C ．26D ．428．已知集合1}{0|A x x -≥=，{0,1,2}B =，则A B =A ．{0}B ．{1}C ．{1,2}D ．{0,1,2}9．已知π,4αβ+=则(1tan )(1tan )αβ++的值是（ ） A ．-1B ．1C ．2D ．410．sin 47sin17cos30cos17-A ．32-B ．12-C ．12D ．3211．函数y ()y ()f x f x ==，的导函数的图像如图所示，则函数y ()f x =的图像可能是A ．B ．C ．D ．12．将函数()sin 2y x ϕ=+的图象沿轴向左平移8π个单位后，得到一个偶函数的图象，则ϕ的一个可能取值为( ) A ．B ．C ．0D ．4π-二、填空题13．函数()22,026,0x x f x x lnx x ⎧-≤=⎨-+>⎩的零点个数是________．14．若不等式|3|4x b -<的解集中的整数有且仅有1，2，3，则b 的取值范围是15．在ABC 中，60A =︒，1b =3sin sin sin a b cA B C ________．16．已知圆锥的侧面展开图是一个半径为2cm ，圆心角为23π的扇形，则此圆锥的高为________cm .17．在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于y 轴对称.若1sin 3α=，则cos()αβ-=___________. 18．已知函数()(ln )f x x x ax =-有两个极值点,则实数a 的取值范围是__________． 19．能说明“若f （x ）>f （0）对任意的x ∈（0，2］都成立，则f （x ）在［0，2］上是增函数”为假命题的一个函数是__________．20．从2位女生，4位男生中选3人参加科技比赛，且至少有1位女生入选，则不同的选法共有_____________种．（用数字填写答案）三、解答题21．某农场有一块农田，如图所示，它的边界由圆O 的一段圆弧MPN （P 为此圆弧的中点）和线段MN 构成．已知圆O 的半径为40米，点P 到MN 的距离为50米．现规划在此农田上修建两个温室大棚，大棚I 内的地块形状为矩形ABCD ，大棚II 内的地块形状为CDP ，要求,A B 均在线段MN 上，,C D 均在圆弧上．设OC 与MN 所成的角为θ．（1）用θ分别表示矩形ABCD 和CDP 的面积，并确定sin θ的取值范围；（2）若大棚I 内种植甲种蔬菜，大棚II 内种植乙种蔬菜，且甲、乙两种蔬菜的单位面积年产值之比为4:3．求当θ为何值时，能使甲、乙两种蔬菜的年总产值最大．22．已知椭圆22221(0)x y a b a b +=>>的离心率为63，以椭圆的2个焦点与1个短轴端点为顶点的三角形的面积为22． （1）求椭圆的方程；（2）如图，斜率为k 的直线l 过椭圆的右焦点F ，且与椭圆交与,A B 两点，以线段AB 为直径的圆截直线1x =所得的弦的长度为5，求直线l 的方程．23．如图，在三棱柱111ABC A B C -中，H 是正方形11AA B B 的中心，122AA =1C H ⊥平面11AA B B ，且1 5.C H =（Ⅰ）求异面直线AC 与11A B 所成角的余弦值； （Ⅱ）求二面角111A AC B --的正弦值；（Ⅲ）设N 为棱11B C 的中点，点M 在平面11AA B B 内，且MN ⊥平面111A B C ，求线段BM 的长．24．已知矩形ABCD 的两条对角线相交于点20M （，），AB 边所在直线的方程为360x y --=，点11T -（，）在AD 边所在直线上. （1）求AD 边所在直线的方程； （2）求矩形ABCD 外接圆的方程.25．商场销售某种商品的经验表明，该商品每日的销售量(单位：千克)与销售价格(单位：元/千克)满足关系式，其中，为常数，已知销售价格为5元/千克时，每日可售出该商品11千克． (1) 求的值；(2) 若商品的成品为3元/千克, 试确定销售价格的值,使商场每日销售该商品所获得的利润最大【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【解析】 【分析】 【详解】::sin :sin :sin 3:2:4a b c A B C == ，不妨设3,2,4a k b k c k ===，,则()()()2223241cos 2324k k k C k k+-==-⨯⨯ ，选A.2．D解析：D 【解析】 【详解】由题意可得 ：5z ==，且：43z i =-，据此有：4343555z i i z -==-. 本题选择D 选项.3．A解析：A 【解析】 【分析】根据函数的奇偶性，排除D ；根据函数解析式可知定义域为{}1x x ≠±,所以y 轴右侧虚线部分为x=1，利用特殊值x=0.01和x=1.001代入即可排除错误选项． 【详解】由函数解析式()22x x e e f x x x --=+-，易知()22x xe ef x x x ---=+-=() f x - 所以函数()22x xe ef x x x --=+-为奇函数，排除D 选项根据解析式分母不为0可知,定义域为{}1x x ≠±,所以y 轴右侧虚线部分为x=1， 当x=0.01时，代入()f x 可得()0f x <，排除C 选项 当x=1.001时，代入()f x 可得()0f x >，排除B 选项 所以选A 【点睛】本题考查了根据函数解析式判断函数的图象，依据主要是奇偶性、单调性、特殊值等，注意图中坐标的位置及特殊直线，属于中档题．4．D解析：D 【解析】因为全称命题的否定是特称命题，所以命题“对任意x ∈R ，都有x 2≥0”的否定为．存在x 0∈R ，使得x 02＜0． 故选D ．5．B解析：B 【解析】试题分析：由题意，这是几何概型问题，班车每30分钟发出一辆，到达发车站的时间总长度为40，等车不超过10分钟的时间长度为20，故所求概率为201402=，选B. 【考点】几何概型【名师点睛】这是全国卷首次考查几何概型,求解几何概型问题的关键是确定“测度”,常见的测度有长度、面积、体积等.6．D解析：D 【解析】 【分析】 【详解】试题分析：A 项中两直线a b ，还可能相交或异面,错误； B 项中两直线a b ，还可能相交或异面,错误； C 项两平面αβ，还可能是相交平面，错误； 故选D.7．D解析：D 【解析】 【分析】2a b+≤转化为指数运算即可求解。

广西高考数学一模试卷（理科）一、选择题（共12小题，每小题5分，满分60分）1．已知集合A={x|﹣1≤x≤1}，B={x|x2﹣2x≤0}，则A∩B=（）A．[﹣1，0] B．[﹣1，2] C．[0，1] D．（﹣∞，1]∪[2，+∞）2．设复数z=1+i，i是虚数单位，则+（）2=（）A．1﹣3i B．1﹣i C．﹣1﹣i D．﹣1+i3．“log22x＞0”是“x＞1”成立的（）A．充分不必要条件B．必要不充分条件C．充要条件 D．既不充分也不必要条件4．下列函数是偶函数，且最小正周期为π的是（）A．y=sin（π﹣2x）B．y=sin2xcos2x C．y=cos22x+1 D．y=cos（2x﹣π）5．阅读如图所示的程序框图，运行相应的程序，若判断框内是n≤6，则输出的S为（）A．B．C．D．6．已知双曲线，它的一个顶点到较近焦点的距离为1，焦点到渐近线的距离是，则双曲线C的方程为（）A．x2﹣=1 B．﹣y2=1 C．﹣y2=1 D．x2﹣=17．已知数列{a n}是等比数列，且a3=1，a5a6a7=8，则a9=（）A．2 B．4 C．6 D．88．一个几何体的三视图如图，则该几何体的表面积为（）A．8+6B．10+8 C．12+4 D．14+29．将函数y=sin2x的图象向左平移φ（φ＞0）个单位，得到g（x）的图象，若g（x）的图象关于直线x=对称，则φ的最小值为（）A．B．C．D．10．若x，y满足不等式组，z=x﹣y的最大值为4，则实数a=（）A．4 B．C．5 D．11．已知圆C：x2+y2﹣2x+4y=0关于直线3x﹣ay﹣11=0对称，则圆C中以（，﹣）为中点的弦长为（）A．1 B．2 C．3 D．412．已知曲线f（x）=e x﹣ax在点（0，f（0））处的切线方程为3x+y+b=0，则下列不等式恒成立的是（）A．f（x）≥2﹣4ln2 B．f（x）≤2﹣4ln2 C．f（x）≥4﹣8ln2 D．f（x）≤4﹣8ln2二、填空题（共4小题，每小题5分，满分20分）13．（2x﹣）6展开式中常数项为（用数字作答）．14．向量=（1，﹣2）与=（3，t）的夹角为θ，=（1，﹣3），⊥，则cosθ=．15．设函数f（x）=，若存在实数b，使函数y=f（x）﹣b有且只有2个零点，则实数b的取值范围是．16．已知等差数列{a n}的前n项和为S n，a1=﹣1，（a n+1﹣4）n=2S n，则S n= ．三、解答题（共5小题，满分60分）17．在三角形ABC中，角A，B，C的对边分别是a，b，c．若b=，c=3，B+C=3A．（1）求边a；（2）求sin（B+）的值．18．某地区交通执法部门从某日上午9时开始对经过当地的200名车辆驾驶人员驾驶的车辆进行超速测试并分组，并根据测速的数据制作了频率分布图：（Ⅱ）若在第2，3，4，5组用分层抽样的方法随机抽取12名驾驶人员做回访调查，并在这12名驾驶人员中任意选3人，这3人中超速在[20%，80%）内的人数记为ξ，求ξ的数学期望．19．如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AC⊥AD，AB⊥BC，PA=AB=BC=1，AC=AD，点E在棱PB上，且PE=2EB．（1）求证：PD∥平面EAC．（2）求平面ACE和平面ABCD所成锐二面角的余弦值．20．已知椭圆G：+=1（a＞b＞0）的离心率为，左顶点为A，上顶点为E，O是坐标原点，△OAE面积为．（1）求椭圆G的方程；（2）若过椭圆G的右焦点作垂直于x轴的直线m与G在第一象限内交于点M，平行于AM的直线l与椭圆G相交于B，C两点，判断直线MB，MC是否关于直线m对称，并说明理由．21．设函数f（x）=x3+ax2+bx（x＞0）的图象与x轴相切于M（3，0）．（1）求f（x）的解析式，并求y=+4lnx的单调减区间；（2）是否存在两个不等正数s，t（x＞t），当x∈[s，t]时，函数f（x）=x3+ax2+bx的值域也是[s，t]，若存在，求出所有这样的正数s，t，若不存在，请说明理由．请在第（22）、（23）、（24)三题中任选一题作答，如果多做，则按所做的第一题记分[选修4-1：几何证明选讲]22．如图，A，B，C，D四点在同一圆上，AB∥CD，AD的延长线与BC的延长线交于E点．（1）证明：EC=ED．（2）延长CD到F，延长DC到G，连接EF、EG，使得EF=EG，证明：A，B，G，F四点共圆．[选修4-4：坐标系与参数方程]23．已知曲线C1的参数方程为（θ为参数），曲线C2的极坐标方程为ρ=2cosθ+6sinθ．（1）将曲线C1的参数方程化为普通方程，将曲线C2的极坐标方程化为直角坐标方程；（2）曲线C1，C2是否相交，若相交请求出公共弦的长，若不相交，请说明理由．[选修4-5：不等式选讲]24．已知函数f（x）=|x﹣1|+|x﹣a|（a∈R）．（1）若a=4，求不等式f（x）≥5的解集；（2）若存在x∈R，使f（x）≤4成立，求a的取值范围．参考答案与试题解析一、选择题（共12小题，每小题5分，满分60分）1．已知集合A={x|﹣1≤x≤1}，B={x|x2﹣2x≤0}，则A∩B=（）A．[﹣1，0] B．[﹣1，2] C．[0，1] D．（﹣∞，1]∪[2，+∞）【考点】交集及其运算．【分析】直接由一元二次不等式化简集合B，则A交B的答案可求．【解答】解：∵B={x|x2﹣2x≤0}={x|0≤x≤2}，∴A∩B={x|﹣1≤x≤1}∩{x|0≤x≤2}={x|0≤x≤1}．则A∩B的区间为：[0，1]．故选C．2．设复数z=1+i，i是虚数单位，则+（）2=（）A．1﹣3i B．1﹣i C．﹣1﹣i D．﹣1+i【考点】复数代数形式的混合运算．【分析】利用复数的运算法则和共轭复数的定义即可得出．【解答】解：复数z=1+i，i是虚数单位，则+（）2=+（1﹣i）2=1﹣i﹣2i=1﹣3i，故选：A3．“log22x＞0”是“x＞1”成立的（）A．充分不必要条件B．必要不充分条件C．充要条件 D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】根据充分条件和必要条件的定义进行判断即可．【解答】解：若log22x＞0，则2x＞1，得x＞0，则“log22x＞0”是“x＞1”成立的必要不充分条件，故选：B．4．下列函数是偶函数，且最小正周期为π的是（）A．y=sin（π﹣2x）B．y=sin2xcos2x C．y=cos22x+1 D．y=cos（2x﹣π）【考点】三角函数的周期性及其求法．【分析】根据正弦型函数及余弦型函数的性质，我们逐一分析四个答案中的四个函数的周期性及奇偶性，然后和题目中的条件进行比照，即可得到答案．【解答】D解：A中，函数y=sin（π﹣2x）=sin2x为奇函数，不满足条件；B中，函数y=sin2xcos2x=sin4x周期为，不满足条件；C中，函数y=cos22x+1=cos4x+周期为，不满足条件；D中，函数y=cos（2x﹣π）=﹣cos2x是最小正周期为π的偶函数，满足条件；故选：D．5．阅读如图所示的程序框图，运行相应的程序，若判断框内是n≤6，则输出的S为（）A．B．C．D．【考点】程序框图．【分析】模拟执行程序框图，依次写出每次循环得到的S，n的值，当n=8时，此时应该不满足条件n≤6，退出循环，输出S的值为．【解答】解：模拟执行程序框图，可得：S=0，n=2满足条件n≤6，S=，n=4满足条件n≤6，S=，n=6满足条件n≤6，S=+=，n=8由题意，此时应该不满足条件n≤6，退出循环，输出S的值为，故选：C．6．已知双曲线，它的一个顶点到较近焦点的距离为1，焦点到渐近线的距离是，则双曲线C的方程为（）A．x2﹣=1 B．﹣y2=1 C．﹣y2=1 D．x2﹣=1【考点】双曲线的简单性质．【分析】由题意可得c﹣a=1，求出渐近线方程和焦点的坐标，运用点到直线的距离公式，可得b=，由a，b，c的关系，可得a，进而得到所求双曲线的方程．【解答】解：双曲线的一个顶点（a，0）到较近焦点（c，0）的距离为1，可得c﹣a=1，由双曲线的渐近线方程为y=x，则焦点（c，0）到渐近线的距离为d==b=，又c2﹣a2=b2=3，解得a=1，c=2，即有双曲线的方程为x2﹣=1．故选：A．7．已知数列{a n}是等比数列，且a3=1，a5a6a7=8，则a9=（）A．2 B．4 C．6 D．8【考点】等比数列的通项公式．【分析】设等比数列{a n}的公比为q，由a3=1，a5a6a7=8，可得=1，=8，解得q3，即可得出．【解答】解：设等比数列{a n}的公比为q，∵a3=1，a5a6a7=8，∴=1，=8，解得q3=2．则a9==4．8．一个几何体的三视图如图，则该几何体的表面积为（）A．8+6B．10+8 C．12+4 D．14+2【考点】由三视图求面积、体积．【分析】由三视图知该几何体是一个直四棱柱，由三视图求出几何元素的长度，由面积公式求出各个面的面积，加起来即可求出几何体的表面积．【解答】解：根据三视图可知几何体是一个直四棱柱，由俯视图知底面是等腰梯形：上底、下底分别是1、3，梯形的高是1，则腰长是，且直四棱柱的高是2，∴几何体的表面积S==12+4，故选：C．9．将函数y=sin2x的图象向左平移φ（φ＞0）个单位，得到g（x）的图象，若g（x）的图象关于直线x=对称，则φ的最小值为（）A． B．C．D．【考点】函数y=Asin（ωx+φ）的图象变换．【分析】由条件利用函数y=Asin（ωx+φ）的图象变换规律，正弦函数的图象的对称性，求得φ的最小值．【解答】解：将函数y=sin2x的图象向左平移φ（φ＞0）个单位，得到g（x）=sin2（x+φ）=sin（2x+2φ）的图象，若g（x）的图象关于直线x=对称，则+2φ=kπ+，k∈Z，则φ的最小值为，故选：A．10．若x，y满足不等式组，z=x﹣y的最大值为4，则实数a=（）A．4 B．C．5 D．【考点】简单线性规划．【分析】作出可行域，变形目标函数，平移直线可得z的最值，可得a的方程，解方程可得．【解答】解：作出不等式组所对应可行域（如图△ABC），变形目标函数z=x﹣y可得y=x﹣z，平移直线y=x可知：当直线经过点A（a，3﹣a）时，直线截距最小值，z取最大值，代值可得a﹣（3﹣a）=4，解得a=，故选：B．11．已知圆C：x2+y2﹣2x+4y=0关于直线3x﹣ay﹣11=0对称，则圆C中以（，﹣）为中点的弦长为（）A．1 B．2 C．3 D．4【考点】直线与圆的位置关系．【分析】由已知直线3x﹣ay﹣11=0过圆心C（1，﹣2），从而得到a=4，点（1，﹣1）到圆心C（1，﹣2）的距离d=1，圆C：x2+y2﹣2x+4y=0的半径r=，由此能求出圆C中以（，﹣）为中点的弦长．【解答】解：∵圆C：x2+y2﹣2x+4y=0关于直线3x﹣ay﹣11=0对称，∴直线3x﹣ay﹣11=0过圆心C（1，﹣2），∴3+2a﹣11=0，解得a=4，∴（，﹣）=（1，﹣1），点（1，﹣1）到圆心C（1，﹣2）的距离d==1，圆C：x2+y2﹣2x+4y=0的半径r==，∴圆C中以（，﹣）为中点的弦长为：2=2=4．故选：D．12．已知曲线f（x）=e x﹣ax在点（0，f（0））处的切线方程为3x+y+b=0，则下列不等式恒成立的是（）A．f（x）≥2﹣4ln2 B．f（x）≤2﹣4ln2 C．f（x）≥4﹣8ln2 D．f（x）≤4﹣8ln2 【考点】利用导数研究曲线上某点切线方程．【分析】求出函数的导数，可得切线的斜率，由切线的方程可得斜率，解方程可得a，求出单调区间、极值和最值，即可得到结论．【解答】解：f（x）=e x﹣ax的导数为f′（x）=e x﹣a，可得在点（0，f（0））处的切线斜率为1﹣a，由切线方程为3x+y+b=0，可得1﹣a=﹣3，即有a=4，可得f′（x）=e x﹣4，当x＞ln4时，f′（x）＞0，f（x）递增；当x＜ln4时，f′（x）＜0，f（x）递减．可得f（x）在x=ln4处取得极小值，也为最小值4﹣8ln2．即为f（x）≥4﹣8ln2．故选：C．二、填空题（共4小题，每小题5分，满分20分）13．（2x﹣）6展开式中常数项为60 （用数字作答）．【考点】二项式定理．【分析】用二项展开式的通项公式得展开式的第r+1项，令x的指数为0得展开式的常数项．【解答】解：（2x﹣）6展开式的通项为=令得r=4故展开式中的常数项．故答案为6014．向量=（1，﹣2）与=（3，t）的夹角为θ，=（1，﹣3），⊥，则cosθ=．【考点】平面向量数量积的运算．【分析】根据向量的数量积的运算和向量的夹角公式计算即可．【解答】解：∵=（1，﹣2）与=（3，t）的夹角为θ，=（1，﹣3），⊥，∴3×1﹣3t=0，∴t=1，∴=（3，1），∴||=，||=，•=1×3﹣2×1=1，∴cosθ==故答案为：．15．设函数f（x）=，若存在实数b，使函数y=f（x）﹣b有且只有2个零点，则实数b的取值范围是（0，+∞）．【考点】函数零点的判定定理．【分析】由题意可得函数f（x）=的图象和直线y=b有2个交点，分类讨论，数形结合求得a的取值范围．【解答】解：由题意可得函数y=f（x）=的图象和直线y=b有且只有2个交点，当a=0 时，f（x）=，如图（1）所示，函数y=f（x）的图象和直线y=b之多有一个交点，不满足条件．当a＞0时，f（x）=的图象如图（2）所示，此时，应有b＞0．当a＜0时，f（x）=的图象如图（3）所示，此时，函数y=f（x）的图象和直线y=b之多有一个交点，不满足条件．综上可得，b＞0，故答案为：（0，+∞）．16．已知等差数列{a n}的前n项和为S n，a1=﹣1，（a n+1﹣4）n=2S n，则S n= ．【考点】等差数列的前n项和．【分析】设等差数列{a n}的公差为d，a1=﹣1，则a n+1=﹣1+nd，S n=﹣n+d，代入（a n+1﹣4）n=2S n，化简整理即可得出．【解答】解：设等差数列{a n}的公差为d，a1=﹣1，则a n+1=﹣1+nd，S n=﹣n+d，代入（a n+1﹣4）n=2S n，可得：（﹣5+nd）n=﹣2n+n（n﹣1）d，化为：d=3．则S n=﹣n+=．故答案为：．三、解答题（共5小题，满分60分）17．在三角形ABC中，角A，B，C的对边分别是a，b，c．若b=，c=3，B+C=3A．（1）求边a；（2）求sin（B+）的值．【考点】正弦定理的应用；两角和与差的正弦函数．【分析】（1）由条件利用余弦定理求得a的值．（2）由条件利用正弦定理求得sinB的值，可得cosB的值，再利用两角和差的正弦公式，求得sin（B+）的值．【解答】解：（1）三角形ABC中，∵b=，c=3，B+C=3A，∴A=，利用余弦定理可得a2=b2+c2﹣2bc•cosA=5，∴a=．（2）由正弦定理=，可得=，∴sinB=，再结合b＜c，可得B为锐角，∴cosB==，∴sin（B+）=sinBcos+cosBsin=+•=．18．某地区交通执法部门从某日上午9时开始对经过当地的200名车辆驾驶人员驾驶的车辆进行超速测试并分组，并根据测速的数据制作了频率分布图：（Ⅱ）若在第2，3，4，5组用分层抽样的方法随机抽取12名驾驶人员做回访调查，并在这12名驾驶人员中任意选3人，这3人中超速在[20%，80%）内的人数记为ξ，求ξ的数学期望．【考点】离散型随机变量的期望与方差；分层抽样方法．【分析】（Ⅰ）由频率=，能求出z，y，x的值．（Ⅱ）若在第2，3，4，5组用分层抽样的方法随机抽取12名驾驶人员，则第2，3，4，5组抽取的人数分别是4，3，2，1，设任意选取的3人超速在（20%，80%）的人数是ξ，则ξ=2或ξ=3，由此能求出ξ的数学期望．【解答】解：（Ⅰ）由题意得x=200×0.01=2，y=6÷200=0.03，z=0.88÷20=0.044．（Ⅱ）若在第2，3，4，5组用分层抽样的方法随机抽取12名驾驶人员，则第2，3，4，5组抽取的人数分别是4，3，2，1，设任意选取的3人超速在（20%，80%）的人数是ξ，则ξ=2或ξ=3，P（ξ=2）==，P（ξ=3）==，∴Eξ==．19．如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AC⊥AD，AB⊥BC，PA=AB=BC=1，AC=AD，点E在棱PB上，且PE=2EB．（1）求证：PD∥平面EAC．（2）求平面ACE和平面ABCD所成锐二面角的余弦值．【考点】二面角的平面角及求法；直线与平面平行的判定．【分析】（1）根据线面平行的判定定理即可证明PD∥平面EAC．（2）建立坐标系，求出平面的法向量，利用向量法即可求平面ACE和平面ABCD所成锐二面角的余弦值．【解答】证明：（1）∵AB⊥BC，AB=BC=1，∴AC=，∠BAC=，∵AC=AD，AC⊥AD，∴CD=2，∠ACD=，∴∠BAC=∠ACD，则AB∥CD，连接BD，交AC于M，连EM，则，又PE=2EB，在△BPD中，，∴PD∥EM，∵PD⊄平面EAC，EM⊂平面EAC，∴PD∥平面EAC（2）建立如图所示的空间坐标系如图：则A（0，0，0），P（0，0，1），B（0，1，0），C（1，1，0），E（0，，），设=（x，y，z）是平面AEC的一个法向量，则=（1，1，0），（0，，），则•=x+y=0，•=y+z=0，得，令y=1，则x=﹣1，z=﹣2，则=（﹣1，1，﹣2），同理平面ABCD的法向量为==（0，0，1），则cos＜，＞==，即平面ACE和平面ABCD所成锐二面角的余弦值是．20．已知椭圆G：+=1（a＞b＞0）的离心率为，左顶点为A，上顶点为E，O是坐标原点，△OAE面积为．（1）求椭圆G的方程；（2）若过椭圆G的右焦点作垂直于x轴的直线m与G在第一象限内交于点M，平行于AM的直线l与椭圆G相交于B，C两点，判断直线MB，MC是否关于直线m对称，并说明理由．【考点】椭圆的简单性质．【分析】（1）运用椭圆的离心率公式和实际行动面积公式，及a，b，c的关系，解得a，b，进而得到椭圆方程；（2）求得椭圆的右焦点坐标，M，A的坐标，求得斜率．可设BC的方程为y=x+t，代入椭圆方程3x2+4y2=12，可得x2+tx+t2﹣3=0，设B（x1，y1），C（x2，y2），运用韦达定理和直线的斜率公式，可得k MB+k MC=0，进而得到直线MB和直线MC关于直线m对称．【解答】解：（1）由题意可得e==，由A（﹣a，0），E（0，b），可得△OAE面积为，即有ab=，又a2﹣b2=c2，解得a=2，b=，c=1，即有椭圆的方程为+=1；（2）椭圆的右焦点为（1，0），可得M（1，），A（﹣2，0），k AM==，设BC的方程为y=x+t，代入椭圆方程3x2+4y2=12，可得x2+tx+t2﹣3=0，设B（x1，y1），C（x2，y2），即有x1+x2=﹣t，x1x2=t2﹣3，由k MB+k MC=+=+===0．即有直线MB和直线MC关于直线m对称．21．设函数f（x）=x3+ax2+bx（x＞0）的图象与x轴相切于M（3，0）．（1）求f（x）的解析式，并求y=+4lnx的单调减区间；（2）是否存在两个不等正数s，t（x＞t），当x∈[s，t]时，函数f（x）=x3+ax2+bx的值域也是[s，t]，若存在，求出所有这样的正数s，t，若不存在，请说明理由．【考点】利用导数研究函数的单调性；利用导数研究曲线上某点切线方程．【分析】（1）由已知得f′（x）=3x2+2ax+b．依题意f（3）=0，f′（3）=0，解方程即可求出f（x）=x3﹣6x2+9x．（2）由函数的定义域是正数知，s＞0，故极值点x=3不在区间[s，t]上，由此利用分类讨论思想能求出不存在正数s，t满足要求．【解答】解：（1）∵f（x）=x3+ax2+bx，∴f′（x）=3x2+2ax+b．依题意则有f（3）=0，f′（3）=0，即27+9a+3b=0，①27+6a+b=0，②解得a=﹣6，b=9，∴f（x）=x3﹣6x2+9x．则y=+4lnx=x2﹣6x+9+4lnx，x＞0，y′=2x﹣6+==，由y′＜0得1＜x＜2，即y=+4lnx的单调减区间为（1，2）．（2）f′（x）=3x2﹣12x+9=3（x﹣1）（x﹣3），由f′（x）=0，得x=1或x=3．列表讨论，得：由函数的定义域是正数知，s＞0，故极值点x=3不在区间[s，t]上，①若极值点1∈[s，t]，此时0＜s≤1≤t＜3，在此区间上f（x）的最大值是4，不可能等于t，故在区间[s，t]上没有极值点；②若f（x）=x3﹣6x2+9x在[s，t]上单调增，即0＜s＜t≤1或3＜s＜t，则，即，解得不合要求．（3）若f（x）=x3﹣6x2+9x在[s，t]上单调减，即1≤s＜t＜3，则，两式相减并除s﹣t，得：（s+t）2﹣6（s+t）﹣st+10=0，①两式相除并开方，得[s（s﹣3）]2=[t（t﹣3）]2，即s（3﹣s）=t（3﹣t），整理，并除以s﹣t，得：s+t=3，②则①、②得，即s，t是方程x2﹣3x+1=0的两根，即s=，t=不合要求；综上，不存在正数s，t满足要求．…请在第（22）、（23）、（24)三题中任选一题作答，如果多做，则按所做的第一题记分[选修4-1：几何证明选讲]22．如图，A，B，C，D四点在同一圆上，AB∥CD，AD的延长线与BC的延长线交于E点．（1）证明：EC=ED．（2）延长CD到F，延长DC到G，连接EF、EG，使得EF=EG，证明：A，B，G，F四点共圆．【考点】与圆有关的比例线段．【分析】（1）根据四点共圆，得到四边形的一个外角等于不相邻的一个内角，根据两直线平行，同位角相等，等量代换得到两个角相等，从而两条边相等，得到结论；（2）根据第一问做出的边和角之间的关系，得到两个三角形全等，根据全等三角形的对应角相等，根据平行的性质定理，等量代换，得到四边形的一对对角相等，得到四点共圆．【解答】（1）证明：因为A，B，C，D四点在同一圆上，所以∠EDC=∠EBA因为CD∥AB，所以∠ECD=∠EBA，所以∠EDC=∠ECD，所以EC=ED．（2）解：由（1）知，AE=BE，因为EF=EG，故∠EFD=∠EGC从而∠FED=∠GEC连接AF，BG，△EFA≌△EGB，故∠FAE=∠GBE又CD∥AB，∠FAB=∠GBA，所以∠AFG+∠GBA=180°故A，B．G，F四点共圆．[选修4-4：坐标系与参数方程]23．已知曲线C1的参数方程为（θ为参数），曲线C2的极坐标方程为ρ=2cosθ+6sinθ．（1）将曲线C1的参数方程化为普通方程，将曲线C2的极坐标方程化为直角坐标方程；（2）曲线C1，C2是否相交，若相交请求出公共弦的长，若不相交，请说明理由．【考点】圆的参数方程；简单曲线的极坐标方程．【分析】（1）根据同角三角函数关系消去参数θ，即可求出曲线C1的普通方程，曲线C2的极坐标方程两边同乘ρ，根据极坐标公式进行化简就可求出直角坐标方程；（2）先求出两个圆心之间的距离与两半径和进行比较，设相交弦长为d，因为两圆半径相等，所以公共弦平分线段C1C2，建立等量关系，解之即可．【解答】解：（1）由得（x+2）2+y2=10∴曲线C1的普通方程为得（x+2）2+y2=10∵ρ=2cosθ+6sinθ∴ρ2=2ρcosθ+6ρsinθ∵ρ2=x2+y2，x=ρcosθ，y=ρsinθ∴x2+y2=2x+6y，即（x﹣1）2+（y﹣3）2=10∴曲线C2的直角坐标方程为（x﹣1）2+（y﹣3）2=10（2）∵圆C1的圆心为（﹣2，0），圆C2的圆心为（1，3）∴∴两圆相交设相交弦长为d，因为两圆半径相等，所以公共弦平分线段C1C2∴∴d=∴公共弦长为[选修4-5：不等式选讲]24．已知函数f（x）=|x﹣1|+|x﹣a|（a∈R）．（1）若a=4，求不等式f（x）≥5的解集；（2）若存在x∈R，使f（x）≤4成立，求a的取值范围．【考点】绝对值不等式的解法；绝对值三角不等式．【分析】（1）不等式即|x﹣1|+|x﹣4|≥5，通过去绝对值符号，列出不等式组，分别求出每个不等式组的解集，再取并集即得所求．（2）利用f（x）=|x﹣1|+|x﹣a|≥|a﹣1|，由题意可得|a﹣1|≤4，由此解得a的范围．【解答】解：（1）解：（Ⅰ）当a=4时，不等式f（x）≥5，即|x﹣1|+|x﹣4|≥5，等价于，或，或．解得：x≤0或x≥5．…故不等式f（x）≥6的解集为{x|x≤0，或x≥5}；（2）∵f（x）=|x﹣1|+|x﹣a|≥|（x﹣1）﹣（x﹣a）|=|a﹣1|．（当x=1时等号成立）所以：f（x）min=|a﹣1|．…由题意得：|a﹣1|≤4，解得：﹣3≤a≤5．…。

2019年广西梧州市高考数学一模试卷（理科）一、单选题（共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符合题目要求)1．（5分）若集合A＝[2，3]，B＝{x|x2﹣5x+6＝0}，则A∩B＝（）A．{2，3}B．∅C．2D．[2，3]2．（5分）已知复数z的实部为﹣1，虚部为2，则＝（）A．2﹣i B．2+i C．﹣2﹣i D．﹣2+i3．（5分）计算log2sin+log2cos的值为（）A．﹣4B．4C．2D．﹣24．（5分）若a，4，3a为等差数列的连续三项，则a0+a1+a2+…+a9的值为（）A．2047B．1062C．1023D．5315．（5分）甲、乙、丙．丁四辆玩具赛车同时从起点出发并做匀速直线运动，丙车最先到达终点．丁车最后到达终点．若甲、乙两车的s﹣t图象如图所示，则对于丙、丁两车的图象所在区域，判断正确的是（）A．丙在Ⅲ区域，丁在Ⅰ区域B．丙在Ⅰ区城，丁在Ⅲ区域C．丙在Ⅱ区域，丁在Ⅰ区域D．丙在Ⅲ区域，丁在Ⅱ区域6．（5分）已知△ABC一边的两个端点是A（7，0），B（﹣7，0），另两边斜率的积是，那么顶点C的轨迹方程是（）A．x2+y2＝49（y≠0）B．＝1（y≠0）C．＝1（y≠0）D．＝1（y≠0）7．（5分）下列四个结论中正确命题的个数是（）①命题“若f（x）是周期函数，则f（x）是三角函数”的否命题是“若f（x）是周期函数，则f（x）不是三角函数”；②命题“∃x0∈R，x02﹣x0﹣1＜0”的否定是“∀x∈R，x2﹣x﹣1≥0”；③在△ABC中，“sin A＞sin B”是“A＞B”的充要条件；④当a＞0时，幂函数y＝x a在区间（0，+∞）上单调递增．A．1个B．2个C．3个D．4个8．（5分）已知函数f（x）＝，则＝（）A．1+B．+C．1+D．+9．（5分）函数f（x）＝（e是自然对数的底数）的图象大致为（）A．B．C．D．10．（5分）已知某几何体的三视图如图所示，则该几何体的表面积为（）A．B．C．13D．11．（5分）设A、B、C、D是半径为2的球面上的四点，且满足AB⊥AC、AD⊥AC、AB ⊥AD，则S△ABC+S△ABD+S△ACD的最大值为（）A．4B．8C．12D．1612．（5分）设函数f（x）是定义在（﹣∞，0）上的可导函数，其导函数为f′（x），且有2f（x）+xf′（x）＞x2，则不等式（x+2019）2f（x+2019）﹣4f（﹣2）＜0的解集为（）A．（﹣2019，﹣2017）B．（﹣2019，﹣2018）C．（﹣2021，﹣2019）D．（﹣2020，﹣2019）二、填空题（本大题共4小题，每小题5分，共20分）13．（5分）已知{a n}是等比数列，若＝（2，a2），＝（3，a3），且∥，则＝．14．（5分）已知圆（x+1）2+y2＝4与抛物线y2＝2px（p＞0）的准线交于A、B两点，且AB ＝2，则p的值为．15．（5分）若f（x）＝（1+x）6（1﹣x）5，f′（x）是f（x）的导函数，则函数f′（x）中x2的系数为．（用数字作答）16．（5分）某计算机程序每运行一次都随机出现一个五位数A＝，其中A的各位数中，a1＝1，a k（k＝2，3，4，5）出现0的概率为，出现1的概率为，记X＝a2+a3+a4+a5，当程序运行一次时，X的数学期望EX＝．三、解答题（共70分．解答应写出文字说明，证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．)17．（12分）在锐角△ABC中，角A，B，C所对的边分别为a，b，c，已知，（1）求的值；（2）若a＝2，，求b的值．18．（12分）基于移动互联技术的共享单车被称为“新四大发明”之一，短时间内就风靡全国，带给人们新的出行体验，某共享单车运营公司的市场研究人员为了解公司的经营状况，对该公司最近六个月的市场占有率t＝y%进行了统计，结果如表：（1）请用相关系数说明能否用线性回归模型拟合y与月份代码x之间的关系，如果能，请计算出y关于x的线性回归方程，并预测该公司2018年12月的市场占有率．如果不能，请说明理由．（2）根据调研数据，公司决定再采购一批单车扩大市场，现有采购成本分别为1000元/辆和800元/辆的A，B两款车型，报废年限各不相同．考虑公司的经济效益，该公司决定对两款单车进行科学模拟测试，得到两款单车使用寿命频数表如表：经测算，平均每辆单车每年可以为公司带来收入500元．不考虑除采购成本以外的其他成本，假设每辆单车的使用寿命都是整数年，用频率估计每辆车使用寿命的概率，分别以这100辆单车所产生的平均利润作为决策依据，如果你是该公司的负责人，会选择釆购哪款车型？参考数据：（x i﹣）2＝17.5，（x i）（y i）＝35，≈36.5参考公式：相关系数r＝回归直线方程＝x+中的斜率和截距的最小二乘估计公式分别为：＝，＝．19．（12分）如图，三棱柱ABC﹣A1B1C1中，侧面BB1C1C是菱形，其对角线的交点为O，且AB＝AC1，AB⊥B1C．（1）求证：AO⊥平面BB1C1C；（2）设∠B1BC＝60°，若直线A1B1与平面BB1C1C所成的角为45°，求二面角A1﹣B1C ﹣A的大小．20．（12分）已知动圆O与x轴切于点A（﹣3，0），又点B（﹣1，0），C（1，0），过B，C分别作圆O′异于x轴的两切线，两切线交于点M．（1）求点M的轨迹Γ的方程；（2）x轴上是否存在定点N，使得过点N的直线l与轨迹Γ交于P，Q时，恒有为定值？若存在，求出定点与定值；若不存在，请说明理由．21．（12分）已知函数f（x）＝ax﹣的两个极值点x1，x2满足x1＜x2，且e＜x2＜3，其中e为自然对数的底数．（Ⅰ）求实数a的取值范围；（Ⅱ）求f（x2）﹣f（x1）的取值范围．请考生在第22、23两题中任选一题作答．注意：只能做选定的题目．如果多做，则按所做的第一题计分．作答时，请用2B铅笔在答题卡上将所选题号后的方框涂黑．[选修4-4：坐标系与参数方程]22．（10分）在直角坐标系xOy中，以原点O为极点，以x轴正半轴为极轴，曲线C的极坐标方程为ρ＝．（Ⅰ）将曲线C的极坐标方程化为直角坐标方程；（Ⅱ）过点P（0，2）作斜率为1直线l与曲线C交于A，B两点，试求+的值．[选修4-5：不等式选讲]23．设函数f（x）＝|3x﹣1|+ax+3．（Ⅰ）若a＝1，解不等式f（x）≤4；（Ⅱ）若函数f（x）有最小值，求a的取值范围．2019年广西梧州市高考数学一模试卷（理科）参考答案与试题解析一、单选题（共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符合题目要求)1．【解答】解：集合A＝[2，3]，B＝{x|x2﹣5x+6＝0|＝{2，3}，则A∩B＝{2，3}．故选：A．2．【解答】解：因为由条件知z＝﹣1+2i，则＝，故选：A．3．【解答】解：∵＝＝2﹣2．∴原式＝＝＝﹣2．故选：D．4．【解答】解：由于a+3a＝4a＝2×4，解得a＝2，故a0+a1+a2+…+a9＝20+21+22+…+29＝．故选：C．5．【解答】解：∵丙车最先到达终点．丁车最后到达终点，∴丙车速度最大，丁车速度最小，∴丙车所在直线的倾斜角最大，丁车所在直线的倾斜角最小．故选：A．6．【解答】解：设顶点A的坐标为（x，y），则；k BC＝，由题意得＝，即＝1（y≠0），故选：D．7．【解答】解：①，命题“若f（x）是周期函数，则f（x）是三角函数”的否命题是：“若f（x）不是周期函数，则f（x）不是三角函数”，故①错误；②，命题“∃x0∈R，x02﹣x0﹣1＜0”的否定是“∀x∈R，x2﹣x﹣1≥0”，故②正确；③，在△ABC中，“sin A＞sin B”⇔“2R sin A＞2R sin B”⇔“a＞b”⇔“A＞B”，故③正确；④，当a＞0时，幂函数y＝x a在区间（0，+∞）上单调递增，故④正确．其中正确命题的个数为3．故选：C．8．【解答】解：＝+＝（）+＝+故选：B．9．【解答】解：f（﹣x）＝＝＝﹣＝﹣f （x），则函数f（x）是奇函数，图象关于原点对称，排除B，C．当x＞1时，f（x）＞0，排除D，故选：A．10．【解答】解由三视图可知几何体为三棱台，作出直观图如图所示，则CC′⊥平面ABC，上下底均为等腰直角三角形，AC⊥BC，AC＝BC＝1，A′C′＝B′C′＝C′C＝2，∴AB＝，A′B′＝2．∴棱台的上底面积为＝，下底面积为＝2，梯形ACC′A′的面积为（1+2）×2＝3，梯形BCC′B′的面积为＝3，过A作AD⊥A′C′于D，过D作DE⊥A′B′，则AD＝CC′＝2，DE为△A′B′C′斜边高的，∴DE＝，∴AE＝＝．∴梯形ABB′A′的面积为（）×＝．∴几何体的表面积S＝＝13．故选：C．11．【解答】解：设AB＝a，AC＝b，AD＝c，因为AB，AC，AD两两互相垂直所以a2+b2+c2＝4×22S△ABC+S△ACD+S△ADB＝（ab+ac+bc）≤（a2+b2+c2）＝8．即最大值8．故选：B．12．【解答】解：由2f（x）+xf′（x）＞x2，（x＜0），得：2xf（x）+x2f′（x）＜x3，即[x2f（x）]′＜x3＜0，令F（x）＝x2f（x），则当x＜0时，得F′（x）＜0，即F（x）在（﹣∞，0）上是减函数，∴F（x+2019）＝（x+2019）2f（x+2019），F（﹣2）＝4f（﹣2），即不等式等价为F（x+2019）﹣F（﹣2）＜0，∵F（x）在（﹣∞，0）是减函数，∴由F（x+2019）＜F（﹣2）得，x+2019＞﹣2，即x＞﹣2021，又x+2019＜0，解得：x＜﹣2019，故﹣2021＜x＜﹣2019，故选：C．二、填空题（本大题共4小题，每小题5分，共20分）13．【解答】解：{a n}是等比数列，若＝（2，a2），＝（3，a3），且∥，可得：3a2＝2a3，所以q＝，则＝＝．故答案为：．14．【解答】解：抛物线y2＝2px（p＞0）的准线为x＝﹣，设A、B两点坐标为（﹣，y1），（﹣，y2），∴（﹣+1）2+y2＝4，即y2＝4﹣（﹣+1）2，∴y＝±，∴|AB|＝|y2﹣y1|＝2＝2，∴4﹣（﹣+1）2＝3，解得p＝4，故答案为：4．15．【解答】解：f（x）＝（1+x）6（1﹣x）5＝（1﹣x2）5（1+x），则（1﹣x2）5的通项公式为：T r+1＝（﹣x2）r，令r＝1，可得：x2的系数为﹣5．∴f（x）的展开式中x3的系数为﹣5×3＝﹣15．故答案为：﹣15．16．【解答】解：由题意可得：X～B，∴EX＝＝．故答案为：．三、解答题（共70分．解答应写出文字说明，证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．)17．【解答】解：（1）因为锐角△ABC中，A+B+C＝π，，所以cos A＝，则＝（2），则bc＝3．将a＝2，cos A＝，c＝代入余弦定理：a2＝b2+c2﹣2bc cos A中得b4﹣6b2+9＝0解得b＝18．【解答】解：（1）＝（11+13+16+15+20+21）＝16，故＝76，故r＝＝＝≈0.96，故两变量之间有较强的相关关系，故可用线性回归模型拟合y与月份代码x之间的关系，＝＝＝2，＝＝16﹣2×3.5＝9，故回归方程是＝2x+9，x＝7时，＝23，即2018年12月的市场占有率是23%；（2）用频率估计概率，这100辆A款单车的平均利率为：（﹣500×10+0×30+500×40+1000×20）＝350（元），这100辆B款车的平均利润为：（﹣300×15+200×40+700×35+1200×10）＝400（元），故会选择釆购B款车型．19．【解答】证明：（1）∵四边形BB1C1C是菱形，∴B1C⊥BC1，∵B1C⊥AB，且BC1∩AB＝B，∴B1C⊥平面ABC1，∴B1C⊥AO，∵AB＝AC1，O是BC1的中点，∴AO⊥BC1，又BC1∩B1C＝O，AO⊥平面BB1C1C．解：（2）∵AB∥A1B1，∴直线A1B1与平面BB1C1C的所成角等于直线AB与平面BB1C1C的所成角，∵AO⊥平面BB1C1C，∴直线AB与平面BB1C1C的所成角为∠ABO，即∠ABO＝45°，设菱形BB1C1C的边长为2，则在等边△BB1C中，BO＝，CO＝B1O＝1，在直角△ABO中，AO＝BO＝，以O为原点建立空间直角坐标系，则B1（0，1，0），C（0，﹣1，0），A1（﹣），＝（），＝（0，﹣2，0），设平面A1B1C的一个法向量为＝（x，y，z），则，取x＝1，得＝（1，0，1），平面AB1C的一个法向量为＝（1，0，0），cos＜＞＝＝，∴二面角A1﹣B1C﹣A的大小为45°．20．【解答】解：（1）过点B的非x轴的切线且圆O′于点E，过点C的非x轴的切线且圆O′于点D，根据切线长性质可得|BA|＝|BE|，|CD|＝|CA|，|MD|＝|ME|，则|MC|＝|CD|﹣|MD|＝|CA|﹣|ME|，①|MB|＝|BE|+|ME|＝|BA|+|CA|，②，①+②可得|MB|+|MC|＝|BA|+|CA|＝4+2＝6，∴点M的轨迹Γ是以B，C为焦点，长轴长为6的椭圆（除去长轴的两顶点），且点M的轨迹Γ的方程是+＝1，（y≠0），（2）设存在定点N（n，0）满足题意，由题意可知直线l的斜率不为零，则设过点N的直线l的方程为x＝my+n，其交点P（x1，y1），Q（x2，y2）不妨设点P在x轴上方，联立直线与椭圆的方程可得（8m2+9）y2+16mny+8n2﹣72＝0，△＝（16mn）2﹣4（8m2+9）（8n2﹣72）＞0，∴y1+y2＝﹣，y1y2＝，∴y2﹣y1＝﹣＝，∴|PN|＝＝＝|y1|＝•y1，∴|PM|＝＝|y2|＝•y2，∴＝﹣＝•＝•，∵m为变量，∴当9﹣n2＝8，即n2＝1时，为定值，此时定点为（1，0），（﹣1，0），故存在定点N（1，0）或（﹣1，0），使得为定值．21．【解答】解：（Ⅰ），f′（x）＝，由题意知x1、x2为方程ax2﹣4x+a＝0的两个根．根据韦达定理得x1+x2＝，x1•x2＝1．整理得a＝．又y＝在（e，3）上单调递增，∴．（Ⅱ）∵f（x2）﹣f（x1）＝﹣ax1++4lnx1，∵，∴f（x2）﹣f（x1）＝﹣+ax2+4ln＝2a（x2﹣）﹣8lnx2，由（Ⅰ）知a＝，代入得f（x2）﹣f（x1）＝（x2﹣）﹣8lnx2＝﹣8lnx2，令t＝x22∈（e2，9），于是可得h（t）＝＝4lnt，故h′（t）＝，∴h（t）在（e2，9）上单调递减，∴f（x2）﹣f（x1）的取值范围为（）．请考生在第22、23两题中任选一题作答．注意：只能做选定的题目．如果多做，则按所做的第一题计分．作答时，请用2B铅笔在答题卡上将所选题号后的方框涂黑．[选修4-4：坐标系与参数方程]22．【解答】解：（I）∵ρ＝，∴ρ2cos2θ＝ρsinθ，∴曲线C的直角坐标方程是x2＝y，即y＝x2．（II）直线l的参数方程为（t为参数）．将（t为参数）代入y＝x2得t2﹣﹣4＝0．∴t1+t2＝，t1t2＝﹣4．∴+＝＝＝＝．[选修4-5：不等式选讲]23．【解答】解：（Ⅰ）当a＝1时，f（x）＝|3x﹣1|+x+3，当x时，f（x）≤4可化为3x﹣1+x+3≤4，解得；当x时，f（x）≤4可化为﹣3x+1+x+3≤4，解得．综上可得，原不等式的解集为{x|}，（Ⅱ）f（x）＝|3x﹣1|+ax+3＝函数f（x）有最小值的充要条件为，即﹣3≤a≤3．。

绝密★启用前广西2019年高考理科数学试卷注意事项：1、答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2、回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3、考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．（5分）已知集合A＝{﹣1，0，1，2}，B＝{x|x2≤1}，则A∩B＝（）A．{﹣1，0，1}B．{0，1}C．{﹣1，1}D．{0，1，2} 2．（5分）若z（1+i）＝2i，则z＝（）A．﹣1﹣i B．﹣1+i C．1﹣i D．1+i3．（5分）《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝，并称为中国古典小说四大名著．某中学为了解本校学生阅读四大名著的情况，随机调查了100位学生，其中阅读过《西游记》或《红楼梦》的学生共有90位，阅读过《红楼梦》的学生共有80位，阅读过《西游记》且阅读过《红楼梦》的学生共有60位，则该校阅读过《西游记》的学生人数与该学校学生总数比值的估计值为（）A．0.5B．0.6C．0.7D．0.84．（5分）（1+2x2）（1+x）4的展开式中x3的系数为（）A．12B．16C．20D．245．（5分）已知各项均为正数的等比数列{a n}的前4项和为15，且a5＝3a3+4a1，则a3＝（）A．16B．8C．4D．26．（5分）已知曲线y＝ae x+xlnx在点（1，ae）处的切线方程为y＝2x+b，则（）A．a＝e，b＝﹣1B．a＝e，b＝1C．a＝e﹣1，b＝1D．a＝e﹣1，b＝﹣1 7．（5分）函数y＝在[﹣6，6]的图象大致为（）A．B．C．D．8．（5分）如图，点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，则（）A．BM＝EN，且直线BM，EN是相交直线B．BM≠EN，且直线BM，EN是相交直线C．BM＝EN，且直线BM，EN是异面直线D．BM≠EN，且直线BM，EN是异面直线9．（5分）执行如图的程序框图，如果输入的ɛ为0.01，则输出s的值等于（）A．2﹣B．2﹣C．2﹣D．2﹣10．（5分）双曲线C：﹣＝1的右焦点为F，点P在C的一条渐近线上，O为坐标原点．若|PO|＝|PF|，则△PFO的面积为（）A．B．C．2D．311．（5分）设f（x）是定义域为R的偶函数，且在（0，+∞）单调递减，则（）A．f（log3）＞f（2）＞f（2）B．f（log3）＞f（2）＞f（2）C．f（2）＞f（2）＞f（log3）D．f（2）＞f（2）＞f（log3）12．（5分）设函数f（x）＝sin（ωx+）（ω＞0），已知f（x）在[0，2π]有且仅有5个零点．下述四个结论：①f（x）在（0，2π）有且仅有3个极大值点②f（x）在（0，2π）有且仅有2个极小值点③f（x）在（0，）单调递增④ω的取值范围是[，）其中所有正确结论的编号是（）A．①④B．②③C．①②③D．①③④二、填空题：本题共4小题，每小题5分，共20分。

广西2019年高考理科数学模拟试题一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．复数21i- (i 为虚数单位)的共轭复数是 A ．1+iB ．1−iC ．−1+iD ．−1−i2．设集合{}{}{}20,1,2,3,4,5,1,2,3,|540U A B x Z x x ===∈-+≥，则()U AB =A ．{}1,2,3B ．{}1,2C ．{}2,3D ．{}23. 下列说法中正确的是A.命题“若22am bm <，则a b <”的逆命题是真命题B.命题“p 或q ”为真命题，则命题p 和命题q 均为真命题C.命题“存在000,1x x ex ∈≤+R ”的否定为：“对,1xx e x ∀∈>+R ”D.直线l 不在平面α内，则“l 上有两个不同的点到α的距离相等”是“//l α”的充要条件 4．设向量a 与b 的夹角为θ，且)1,2(-=a ，)3,2(2=+b a ，则θcos ＝ A. 35- B.35 C.55 D.255- 5．已知α是第四象限角，且1sin cos 5αα+=，则tan 2α=A ．13 B ．13- C ．12D ．12-6. 已知数列}{n a 为等比数列，274=+a a ，865-=⋅a a ，则101a a +的值为A. 7B.5C.7-D.5-7. 设不等式组-20+200x y x y x ≤⎧⎪-≥⎨⎪≥⎩表示的平面区域为Ω.则A. 原点O 在Ω内B.Ω的面积是1C. Ω内的点到y 轴的距离有最大值D.若点P(x 0,y 0) ∈Ω，则x 0+y 0≠08．如右图是寻找“徽数”的程序框图．其中“S MOD 10”表示自然数S 被10除所得的余数，“S \10”表示自然数S 被10除所得的商．则 根据上述程序框图，输出的“徽数”S 为 A ．18B ．16C ．14D ．129. 已知边长为2的等边三角形ABC ，D 为BC 的中点，以AD 为折痕进行翻折，使BDC ∠为直角，则过A B C D ，，，四点的球的表面积为A ．3πB ．4π C.5π D ．6π10．下图来自古希腊数学家希波克拉底所研究的几何图形．此图由三个半圆构成，三个半圆的直径分别为直角三角形ABC 的斜边BC ，直角边AB ，AC ．△ABC 的三边所围成的区域记为I ，黑色部分记为II ，其余部分记为III ．在整个图形中随机取一点，此点取自I ，II ，III 的概率分别记为p 1，p 2，p 3，则A ．p 1=p 2B ．p 1=p 3C ．p 2=p 3D ．p 1=p 2+p 311．根据需要安排甲、乙、丙三人在某月1日至12日值班，每人4天．甲说：我在1日和3日都有值班； 乙说：我在8日和9日都有值班；丙说：我们三人各自值班的日期之和相等．据此可判断丙必定值班的日期是 A ．2日和5日 B ．5日和6日 C ．6日和11日 D ．2日和11日 12．椭圆)0(12222>>=+b a by ax 的左右焦点分别为12,F F ，A 为椭圆上一动点（异于左右顶点），若△12AF F 的周长为6且面积的最大值为3，则椭圆的标准方程为A. 22143y x +=B. 22132y x +=C. 2212x y +=D. 2214x y +=二、填空题（本题共4小题，每小题5分，共20分）13. 设集合{}22(,)|(3sin )(3cos )1,A x y x y R ααα=+++=∈，{}(,)|34100B x y x y =++=，记P AB =，则点集P 所表示的轨迹长度为 。

广西省梧州市2019-2020学年高考数学一月模拟试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知四棱锥P ABCD -中，PA ⊥平面ABCD ，底面ABCD 是边长为2的正方形，5PA =，E 为PC 的中点，则异面直线BE 与PD 所成角的余弦值为（ ） A．13- B ．13 C ．15- D ．15 【答案】B【解析】【分析】由题意建立空间直角坐标系，表示出各点坐标后，利用cos ,BE PD BE PD BE PD⋅=⋅u u u r u u u r u u u r u u u r u u u r u u u r 即可得解. 【详解】Q PA ⊥平面ABCD ，底面ABCD 是边长为2的正方形，∴如图建立空间直角坐标系，由题意：()0,0,0A ，()2,0,0B ，()2,2,0C ，()0,0,5P ，()0,2,0D ，Q E 为PC 的中点，∴51,1,E ⎛⎫ ⎪ ⎪⎝⎭. ∴51,1,BE ⎛⎫=- ⎪ ⎪⎝⎭u u u r ，()0,2,5PD =-u u u r ， ∴1132cos ,1332BE PD BE PD BE PD -⋅===-⋅⋅u u u r u u u r u u u r u u u r u u u r u u u r ， ∴异面直线BE 与PD 所成角的余弦值为cos ,BE PD u u u r u u u r 即为13. 故选：B.【点睛】本题考查了空间向量的应用，考查了空间想象能力，属于基础题.2．在三角形ABC 中，1a =，sin sin sin sin b c a b A A B C++=+-，求sin b A =（ ）A ．2B ．3C ．12D ．2【答案】A【解析】【分析】利用正弦定理边角互化思想结合余弦定理可求得角B 的值，再利用正弦定理可求得sin b A 的值.【详解】sin sin sin sin b c a b A A B C ++=+-Q ，由正弦定理得b c a b a a b c++=+-，整理得222a c b ac +-=， 由余弦定理得2221cos 22a cb B ac +-==，0B Q π<<，3B π∴=.由正弦定理sin sin a b A B =得sin sin 1sin 3b A a B π==⨯=. 故选：A.【点睛】本题考查利用正弦定理求值，涉及正弦定理边角互化思想以及余弦定理的应用，考查计算能力，属于中等题.3．已知抛物线24y x =的焦点为F ，P 为抛物线上一点，(1,1)A ，当PAF ∆周长最小时，PF 所在直线的斜率为（ ）A ．43-B ．34-C ．34D ．43【答案】A【解析】【分析】本道题绘图发现三角形周长最小时A,P 位于同一水平线上，计算点P 的坐标，计算斜率，即可．【详解】结合题意，绘制图像要计算三角形PAF 周长最小值，即计算PA+PF 最小值，结合抛物线性质可知，PF=PN ，所以PF PA PA PN AN AG +=+≥≥，故当点P 运动到M 点处，三角形周长最小，故此时M 的坐标为1,14⎛⎫⎪⎝⎭，所以斜率为1041314k -==--，故选A ． 【点睛】 本道题考查了抛物线的基本性质，难度中等．4．如图示，三棱锥P ABC -的底面ABC 是等腰直角三角形，90ACB ∠=︒，且2PA PB AB ===，3PC =，则PC 与面PAB 所成角的正弦值等于（ ）A ．13B ．63C 3D ．23【答案】A【解析】【分析】首先找出PC 与面PAB 所成角，根据所成角所在三角形利用余弦定理求出所成角的余弦值，再根据同角三角函数关系求出所成角的正弦值.【详解】由题知ABC V 是等腰直角三角形且90ACB ∠=︒，ABP △是等边三角形，设AB 中点为O ，连接PO ，CO ，可知62PO =，2CO = 同时易知AB PO ⊥，AB CO ⊥， 所以AB ⊥面POC ，故POC ∠即为PC 与面PAB 所成角， 有22222cos 23PO CO PC POC PO CO +-∠==⋅， 故1sin 1cos 3POC POC ∠=-∠=. 故选：A.【点睛】本题主要考查了空间几何题中线面夹角的计算，属于基础题.5．将函数()sin 2f x x =的图象向左平移02πϕϕ⎛⎫≤≤⎪⎝⎭个单位长度，得到的函数为偶函数，则ϕ的值为（ ）A ．12πB ．6πC ．3πD ．4π 【答案】D【解析】【分析】利用三角函数的图象变换求得函数的解析式，再根据三角函数的性质，即可求解，得到答案．【详解】将将函数()sin 2f x x =的图象向左平移ϕ个单位长度，可得函数()sin[2()]sin(22)g x x x ϕϕ=+=+又由函数()g x 为偶函数，所以2,2k k Z πϕπ=+∈，解得,42k k Z ππϕ=+∈， 因为02πϕ≤≤，当0k =时，4πϕ=，故选D ．【点睛】本题主要考查了三角函数的图象变换，以及三角函数的性质的应用，其中解答中熟记三角函数的图象变换，合理应用三角函数的图象与性质是解答的关键，着重考查了推理与运算能力，属于基础题．6．已知||23zz i=-（i为虚数单位，z为z的共轭复数），则复数z在复平面内对应的点在（）. A．第一象限B．第二象限C．第三象限D．第四象限【答案】D【解析】【分析】设i,(,)z a b a b R=+∈，由||23zz i=-，得222i=(2)i=3a bz a b+--+，利用复数相等建立方程组即可.【详解】设i,(,)z a b a b R=+∈，则222i=(2)i=3a bz a b+--+，所以22320a bab⎧+⎪=⎨⎪+=⎩，解得222ab⎧=⎪⎨⎪=-⎩，故22i2z=-，复数z在复平面内对应的点为2(,2)2-，在第四象限.故选：D.【点睛】本题考查复数的几何意义，涉及到共轭复数的定义、复数的模等知识，考查学生的基本计算能力，是一道容易题.7．如图是国家统计局于2020年1月9日发布的2018年12月到2019年12月全国居民消费价格的涨跌幅情况折线图.（注：同比是指本期与同期作对比；环比是指本期与上期作对比.如：2019年2月与2018年2月相比较称同比，2019年2月与2019年1月相比较称环比）根据该折线图，下列结论错误的是（）A．2019年12月份，全国居民消费价格环比持平B．2018年12月至2019年12月全国居民消费价格环比均上涨C．2018年12月至2019年12月全国居民消费价格同比均上涨D ．2018年11月的全国居民消费价格高于2017年12月的全国居民消费价格【答案】D【解析】【分析】先对图表数据的分析处理，再结简单的合情推理一一检验即可【详解】由折线图易知A 、C 正确；2019年3月份及6月份的全国居民消费价格环比是负的，所以B 错误；设2018年12月份，2018年11月份，2017年12月份的全国居民消费价格分别为,,a b c ，由题意可知，b a =，1.9%a c c -=，则有1 1.9%a c ab =<=+，所以D 正确. 故选：D【点睛】此题考查了对图表数据的分析处理能力及进行简单的合情推理，属于中档题.8．如图，PA ⊥平面ABCD ，ABCD 为正方形，且PA AD =，E ，F 分别是线段PA ，CD 的中点，则异面直线EF 与BD 所成角的余弦值为（ ）A 2B ．3C 3D 2 【答案】C【解析】【分析】分别以AB ，AD ，AP 所在直线为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系A xyz -,再利用向量法求异面直线EF 与BD 所成角的余弦值.【详解】由题可知，分别以AB ，AD ，AP 所在直线为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系A xyz -.设2AD =.则3(2,2,0),(1,2,1),cos ,86BD EF BD EF =-=-〈〉==⨯u u u r u u u r u u u r u u u r . 故异面直线EF 与BD 3故选：C【点睛】本题主要考查空间向量和异面直线所成的角的向量求法，意在考查学生对这些知识的理解掌握水平. 9．设1F ，2F 分别为双曲线22221x y a b-=（a ＞0，b ＞0）的左、右焦点，过点1F 作圆222x y b += 的切线与双曲线的左支交于点P ，若212PF PF =，则双曲线的离心率为（ ）A 2B 3C 5D 6 【答案】C【解析】【分析】设过点1F 作圆222x y b += 的切线的切点为T ，根据切线的性质可得1OT PF ⊥，且||OT a =，再由212PF PF =和双曲线的定义可得12||2,||4PF a PF a ==，得出T 为1F P 中点，则有2//OT PF ，得到21PF PF ⊥，即可求解.【详解】设过点1F 作圆222x y b += 的切线的切点为T ，22111,||||OT PF FT OF b a ∴⊥=-= 2121212,2,4,2PF PF PF PF a PF a PF a =-===，所以T 是1F P 中点，212//,OT PF PF PF ∴∴⊥，22221212||||20||4PF PF a F F c ∴+===，225,c e a=∴=故选:C.【点睛】本题考查双曲线的性质、双曲线定义、圆的切线性质，意在考查直观想象、逻辑推理和数学计算能力，属于中档题.10．已知()f x 为定义在R 上的奇函数，且满足f x f x (4)(),+=当(0,2)x ∈时，2()2f x x =，则(3)f =（ ）A ．18-B ．18C ．2-D ．2【答案】C【解析】【分析】由题设条件()()4f x f x +=，可得函数的周期是4，再结合函数是奇函数的性质将()3f 转化为()1f 函数值，即可得到结论.【详解】由题意，()()4f x f x +=，则函数()f x 的周期是4，所以，()()()3341f f f =-=-，又函数()f x 为R 上的奇函数，且当()0,2x ∈时，()22f x x =， 所以，()()()3112f f f =-=-=-.故选：C.【点睛】本题考查函数的周期性，由题设得函数的周期是解答本题的关键，属于基础题.11．已知命题300:2,80p x x ∃>->，那么p ⌝为（ ） A ．3002,80x x ∃>-≤B ．32,80x x ∀>-≤C ．3002,80x x ∃≤-≤D ．32,80x x ∀≤-≤【答案】B【解析】【分析】利用特称命题的否定分析解答得解.【详解】已知命题0:2p x ∃>，3080x ->，那么p ⌝是32,80x x ∀>-≤. 故选：B ．【点睛】本题主要考查特称命题的否定，意在考查学生对该知识的理解掌握水平，属于基础题.12．已知点A 是抛物线24x y =的对称轴与准线的交点，点F 为抛物线的焦点，点P 在抛物线上且满足PA m PF =，若m 取得最大值时，点P 恰好在以,A F 为焦点的椭圆上，则椭圆的离心率为（ ） A1B1 C．12 D．12【答案】B【解析】【分析】设(),P x y ，利用两点间的距离公式求出m 的表达式，结合基本不等式的性质求出m 的最大值时的P 点坐标，结合椭圆的定义以及椭圆的离心率公式求解即可.【详解】设(),P x y ，因为A 是抛物线24x y =的对称轴与准线的交点，点F 为抛物线的焦点， 所以()()0,1,0,1A F -， 则PAm PF ==== 当0y =时，1m =，当0y >时，m ==≤= 当且仅当1y =时取等号，∴此时()2,1P±，2PA PF ==， Q 点P 在以,A F 为焦点的椭圆上，22c AF ==，∴由椭圆的定义得22a PA PF =+=，所以椭圆的离心率212c c e a a ====，故选B.【点睛】本题主要考查椭圆的定义及离心率，属于难题.离心率的求解在圆锥曲线的考查中是一个重点也是难点，一般求离心率有以下几种情况：①直接求出,a c ，从而求出e ;②构造,a c 的齐次式，求出e ;③采用离心率的定义以及圆锥曲线的定义来求解．二、填空题：本题共4小题，每小题5分，共20分。