现代控制理论第五章

第五章 Lyapunov稳定性分析和二次型最优控制5.1 概述本章首先讨论Lyapunov稳定性分析，然后介绍线性二次型最优控制问题。

我们将使用Lyapunov稳定性方法作为线性二次型最优控制系统设计的基础。

应用于线性定常系统的稳定性分析方法很多。

然而，对于非线性系统和线性时变系统，这些稳定性分析方法实现起来可能非常困难，甚至是不可能的。

Lyapunov稳定性分析是解决非线性系统稳定性问题的一般方法。

虽然在非线性系统的稳定性问题中，Lyapunov稳定性分析方法具有基础性的地位，但在具体确定许多非线性系统的稳定性时，却并不是直截了当的。

技巧和经验在解决非线性问题时显得非常重要。

在本章中，对于实际非线性系统的稳定性分析仅限于几种简单的情况。

本章5.1节为概述。

5.2节介绍Lyapunov意义下的稳定性定义。

5.3节给出Lyapunov稳定性定理，并将其应用于非线性系统的稳定性分析。

5.4节讨论线性定常系统的Lyapunov稳定性分析。

5.5节给出模型参考控制系统，首先用公式表示Lyapunov稳定性条件，然后在这些条件的限制下设计系统。

5.6节讨论线性二次型最优控制系统，将采用Lyapunov稳定性方程导出线性二次型最优控制的条件。

5.7节给出线性二次型最优控制问题的MATLAB解法。

5.2 Lyapunov意义下的稳定性问题对于一个给定的控制系统，稳定性分析通常是最重要的。

如果系统是线性定常的，那么有许多稳定性判据，如Routh-Hurwitz稳定性判据和Nyquist稳定性判据等可资利用。

然而，如果系统是非线性的，或是线性时变的，则上述稳定性判据就将不再适用。

本节所要介绍的Lyapunov第二法（也称Lyapunov直接法）是确定非线性系统和线性时变系统的最一般的方法。

当然，这种方法也可适用于线性定常系统的稳定性分析。

此外，它还可应用于线性二次型最优控制问题。

5.2.1 平衡状态、给定运动与扰动方程之原点考虑如下非线性系统),(t x f x = (5.1)式中x 为n 维状态向量，),(t x f 是变量x 1,x 2,…,x n 和t 的n 维向量函数。

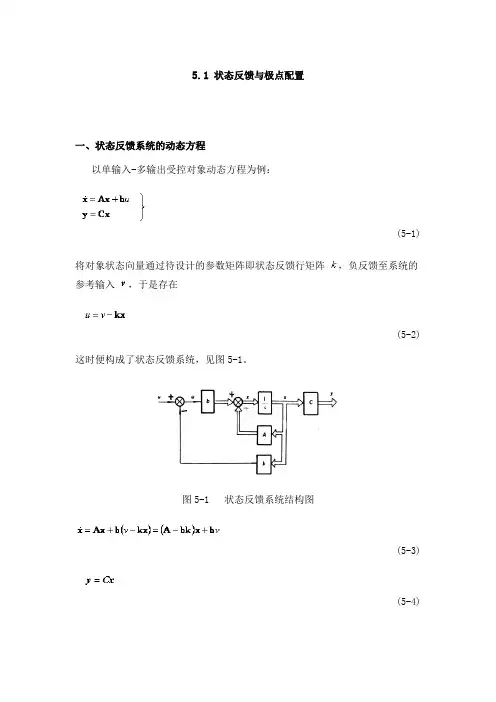
5.1状态反馈与极点配置一、状态反馈系统的动态方程以单输入-多输出受控对象动态方程为例：(5-1)将对象状态向量通过待设计的参数矩阵即状态反馈行矩阵，负反馈至系统的参考输入，于是存在(5-2)这时便构成了状态反馈系统，见图5-1。

图5-1 状态反馈系统结构图(5-3)(5-4)式中v为纯量，为维向量，为维矩阵，为维向量，为维行矩阵，为维向量，为维矩阵。

为闭环状态阵，为闭环特征多项式。

二、用状态反馈使闭环极点配置在任意位置上的充要条件是：受控对象能控证明若式(5-1)所示对象可控，定可通过变换化为能控标准形，有若在变换后的状态空间内引维状态反馈矩阵：(5-5)其中分别为由状态变量引出的反馈系数，则变换后的状态反馈系统动态方程为：(5-6)(5-7)式中(5-8)该式与仍为能控标准形，故引入状态反馈后，系统能控性不变。

特征方程为：(5-9)显见，任意选择阵的个元素，可使特征方程的个系数满足规定要求，能保证特征值（即闭环极点）任意配置。

将逆变换代入式(5-6)，可求出原状态空间内的状态反馈系统状态方程：(5-10)与式(5-3)相比，式(5-10)所示对象应引入状态反馈阵为：(5-11)需指出，当受控对象可控时，若不具有能控标准形形式，并不必象如上证明那样去化为能控标准形，只要直接计算状态反馈系统闭环特征多项式，这时，其系数为的函数，与给定极点的特征多项式系数相比较，便可确定。

能控的多输入-多输出系统，经如上类似分析可知，实现闭环极点任意配置的状态反馈阵K为维。

若受控对象不稳定，只要有能控性，完全可由状态反馈配置极点使系统稳定。

状态变量受控情况下，引入状态反馈表示增加一条反馈通路，它能改变反馈所包围环节的传递特性，即通过改变局部回路的极点来改变闭环极点配置。

不能控状态变量与控制量无关，即使引入状态反馈，对闭环极点位置也不会产生任何影响，这是因为传递函数只与系统能控、能观测部分有关的缘故。

若不能控状态变量是稳定的状态变量，那么系统还是能稳定的，否则，系统不稳定。

《现代控制理论》第5章习题解答5.1 已知系统的状态空间模型为Cx y Bu Ax x =+=, ，画出加入状态反馈后的系统结构图，写出其状态空间表达式。

答：具有状态反馈的闭环系统状态空间模型为：u Kx =−+v ()xA BK x Bv y Cx=−+=相应的闭环系统结构图为闭环系统结构图5.2画出状态反馈和输出反馈的结构图，并写出状态反馈和输出反馈的闭环系统状态空间模型。

答：具有状态反馈的闭环系统状态空间模型为u Kx =−+v ()xA BK x Bv y Cx=−+=相应的反馈控制系统结构图为具有输出反馈的闭环系统状态空间模型为u Fy =−+v ()x A BFC x Bv y Cx=−+=相应的反馈控制系统结构图为后案网 ww w.kh d5.3 状态反馈对系统的能控性和能观性有什么影响？输出反馈对系统能控性和能观性的影响如何？答：状态反馈不改变系统的能控性，但不一定能保持系统的能观性。

输出反馈不改变系统的能控性和能观性。

5.4 通过检验能控性矩阵是否满秩的方法证明定理5.1.1。

答：加入状态反馈后得到闭环系统K S ，其状态空间模型为()x A BK x Bv y Cx=−+=开环系统的能控性矩阵为0S 1[,][]n c A B BAB A B −Γ="闭环系统K S 的能控性矩阵为 1[(),][()()]n cK A BK B B A BK B A BK B −Γ−=−−"由于222()()()()(A BK B AB BKBA BKB A ABK BKA BKBK B)A B AB KB B KAB KBKB −=−−=−−+=−−−#以此类推，总可以写成的线性组合。

因此，存在一个适当非奇异的矩阵U ，使得()m A BK B −1,,,m m A B A B AB B −[(),][,]cK c A BK B A B U Γ−=Γ由此可得：若rank([,])c A B n Γ=，即有个线性无关的列向量，则n [(),]cK A BK B Γ−也有个线性无关的列向量，故n rank([(),])cK A BK B n Γ−=5.5 状态反馈和输出反馈各有什么优缺点。

第五章 状态反馈和状态观测器3-5-1 已知系统结构图如图题3-5-1图所示。

(1)写出系统状态空间表达式；(2)试设计一个状态反馈矩阵，将闭环极点特征值配置在j 53±-上。

)(t y题3-5-1图【解】：方法一：根据系统结构直接设状态变量如题3-5-1图所示，写状态空间表达式：[]x y u x x10112101=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡--=23111=⎥⎦⎤⎢⎣⎡--=cc Urank U系统能控，可以设计状态反馈阵。

设状态反馈阵为][21k k K = 状态反馈控制规律为：Kxr u -=求希望特征多项式：34625)3()(*22++=++=s s s s f求加入反馈后的系统特征多项式：)22()3()(1212k s k k sbK A sI s f ++-++=+-=依据极点配置的定义求反馈矩阵：]1316[131634)22(6)3(21112=⎩⎨⎧==⇒⎩⎨⎧=+=+-K k k k k k方法二：[][][]1316)346(311110)(*10211=++⎥⎦⎤⎢⎣⎡--==--I A AA f U K c方法三：（若不考虑原受控对象的结构，仅从配置极点位置的角度出发） 求系统传递函数写出能控标准型：2321)111()()(2++-=+-+=s sss s s U s Y[]xy u x x10103210-=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=求系统希望特征多项式：34625)3()(*22++=++=s s s s f求状态反馈矩阵K ~：[][][]33236234~21=--==k k K[][][][]5.05.031111010111=⎥⎦⎤⎢⎣⎡--==--Ab b P⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=105.05.011A P P P[]1316~==P K K【解】：依据系统传递函数写出能控标准型sss s s s s U s Y 2310)2)(1(10)()(23++=++=[]xy u x x0010100320100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=求系统希望特征多项式：464]1)1)[(2()(*232+++=+++=s s s s s s f求状态反馈矩阵：[][][]144342604321=---==k k k K 。

现代控制理论第五章习题答案5-1已知系统状态方程为：111001101011x x u -⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦试设计一状态反馈阵使闭环系统极点配置为-1，-2，-3。

解：依题意有：2011012112M bAbA b ⎡⎤⎢⎥⎡⎤==⎣⎦⎢⎥⎢⎥⎣⎦3r a n k M =， 系统能控。

系统0(,,)A b C =∑的特征多项式为： 332(1)(1)1321I A λλλλλλ-=---+=-++则将系统写成能控标准I 型，则有010*********x x u ⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦。

引入状态反馈后，系统的状态方程为：()x A bK x bu =++ ，其中3K ⨯为1矩阵，设[]012K k k k =，则系统(,,)KA bK C =∑的特征多项式为：32210()det[()](3)(2)(1)f I A bK k k k λλλλλ=-+=+--+-+-根据给定的极点值，得到期望特征多项式为：*32()(1)(2)(3)6116f λλλλλλλ=+++=+++比较*()()f f λλ与各对应项系数，可解得：012599k k k =-=-=-，则有：[]-5-9-9K =。

5-3有系统：[]21001110x x u y x-⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦= （1） 画出模拟结构图。

（2） 若动态性能不满足要求，可否任意配置极点？ （3） 若指定极点为-3，-3，求状态反馈阵。

解（1）系统模拟结构图如下：（2）系统采用状态反馈任意配置极点的充要条件是系统(,,)A b C =∑完全能控。

1110011,01011A b -⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦对于系统0(,,)A b C =∑有：[]0111M b Ab ⎡⎤==⎢⎥-⎣⎦2rankM =，系统能控，故若系统动态性能不满足要求，可任意配置极点。

（3）系统(,,)A b C =∑的特征多项式为：2(2)(1)32I A λλλλλ-=++=++则将系统写成能控标准I 型，则有010231x x u⎡⎤⎡⎤=+⎢⎥⎢⎥--⎣⎦⎣⎦。