现代控制理论第一章01

现代控制理论知识点汇总Revised at 2 pm on December 25, 2020.第一章 控制系统的状态空间表达式１． 状态空间表达式 n 阶DuCx y Bu Ax x+=+= 1:⨯r u 1:⨯m y n n A ⨯: r n B ⨯: n m C ⨯:r m D ⨯:A 称为系统矩阵，描述系统内部状态之间的联系；Ｂ为输入（或控制）矩阵，表示输入对每个状态变量的作用情况；C 输出矩阵，表示输出与每个状态变量间的组成关系，Ｄ直接传递矩阵，表示输入对输出的直接传递关系。

２． 状态空间描述的特点①考虑了“输入－状态－输出”这一过程，它揭示了问题的本质，即输入引起了状态的变化，而状态决定了输出。

②状态方程和输出方程都是运动方程。

③状态变量个数等于系统包含的独立贮能元件的个数，n 阶系统有n 个状态变量可以选择。

④状态变量的选择不唯一。

⑤从便于控制系统的构成来说，把状态变量选为可测量或可观察的量更为合适。

⑥建立状态空间描述的步骤：a 选择状态变量；b 列写微分方程并化为状态变量的一阶微分方程组；c 将一阶微分方程组化为向量矩阵形式，即为状态空间描述。

⑦状态空间分析法是时域内的一种矩阵运算方法，特别适合于用计算机计算。

３． 模拟结构图（积分器 加法器 比例器）已知状态空间描述，绘制模拟结构图的步骤：积分器的数目应等于状态变量数，将他们画在适当的位置，每个积分器的输出表示相应的某个状态变量，然后根据状态空间表达式画出相应的加法器和比例器，最后用箭头将这些元件连接起来。

４． 状态空间表达式的建立① 由系统框图建立状态空间表达式：a 将各个环节（放大、积分、惯性等）变成相应的模拟结构图；b 每个积分器的输出选作i x ，输入则为i x；c 由模拟图写出状态方程和输出方程。

② 由系统的机理出发建立状态空间表达式：如电路系统。

通常选电容上的电压和电感上的电流作为状态变量。

利用KVL 和KCL 列微分方程，整理。

１．状态空间表达式n 阶DuCx y Bu Ax x+=+= 1:⨯r u 1:⨯m y n n A ⨯:r n B ⨯:n m C ⨯:rm D ⨯:A 称为系统矩阵，描述系统内部状态之间的联系；Ｂ为输入（或控制）矩阵，表示输入对每个状态变量的作用情况；C 输出矩阵，表示输出与每个状态变量间的组成关系，Ｄ直接传递矩阵，表示输入对输出的直接传递关系。

２．状态空间描述的特点①考虑了“输入－状态－输出”这一过程，它揭示了问题的本质，即输入引起了状态的变化，而状态决定了输出。

②状态方程和输出方程都是运动方程。

③状态变量个数等于系统包含的独立贮能元件的个数，n 阶系统有n 个状态变量可以选择。

④状态变量的选择不唯一。

⑤从便于控制系统的构成来说，把状态变量选为可测量或可观察的量更为合适。

⑥建立状态空间描述的步骤：a 选择状态变量；b 列写微分方程并化为状态变量的一阶微分方程组；c 将一阶微分方程组化为向量矩阵形式，即为状态空间描述。

⑦状态空间分析法是时域内的一种矩阵运算方法，特别适合于用计算机计算。

３．模拟结构图（积分器加法器比例器）已知状态空间描述，绘制模拟结构图的步骤：积分器的数目应等于状态变量数，将他们画在适当的位置，每个积分器的输出表示相应的某个状态变量，然后根据状态空间表达式画出相应的加法器和比例器，最后用箭头将这些元件连接起来。

４．状态空间表达式的建立1由系统框图建立状态空间表达式：a 将各个环节（放大、积分、惯性等）变成相应的模拟结构图；b 每个积分器的输出选作i x ，输入则为i x；c 由模拟图写出状态方程和输出方程。

2由系统的机理出发建立状态空间表达式：如电路系统。

通常选电容上的电压和电感上的电流作为状态变量。

利用KVL 和KCL 列微分方程，整理。

③由描述系统的输入输出动态方程式（微分方程）或传递函数，建立系统的状态空间表达式，即实现问题。

实现是非唯一的。

方法：微分方程→系统函数→模拟结构图→状态空间表达式。

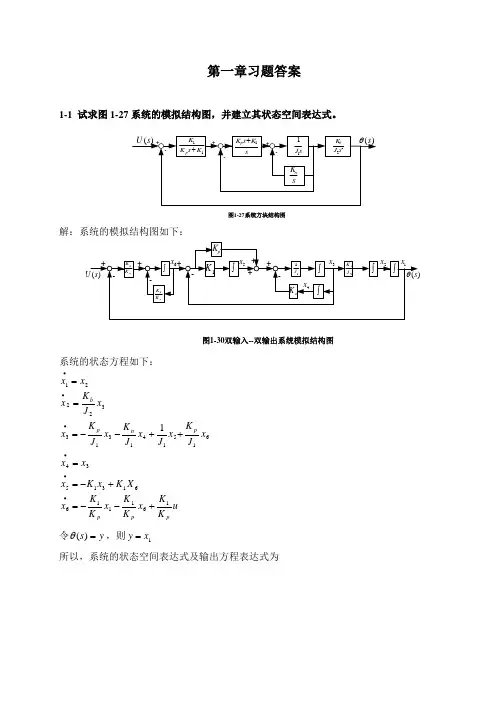
第一章习题答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解：系统的模拟结构图如下：)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下：uKK x KK x KK x X K x K x x x x J Kx J x J K x J Kx x J K x x x ppppn pb 1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙65432116543211111111265432100000100000000000000010010000000000010x x x x x x y uK K x x x xx x K K K K K K J K J J K J KJ K x x x x x xp p pp n pb1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x Cx Cx x L x L R x uL x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000010111010x x x R y u L x x x CCL L R L L R x x x 。

《现代控制理论》第一章习题解答1.1线性定常系统和线性时变系统的区别何在？答：线性系统的状态空间模型为：x = AxBu+y CxDu= +线性定常系统和线性时变系统的区别在于：对于线性定常系统，上述状态空间模型中的系数矩阵A，B，C和中的各分量均为常数，而对线性时变系统，其系数矩阵D A，B，C和D中有时变的元素。

线性定常系统在物理上代表结构和参数都不随时间变化的一类系统，而线性时变系统的参数则随时间的变化而变化。

1.2 现代控制理论中的状态空间模型与经典控制理论中的传递函数有什么区别？答: 传递函数模型与状态空间模型的主要区别如下:1.3 线性系统的状态空间模型有哪几种标准形式？它们分别具有什么特点？答: 线性系统的状态空间模型标准形式有能控标准型、能观标准型和对角线标准型。

对于n 阶传递函数G s( )= b s n−s1nn+−1a s+n−b s1n−n2−1n+−2 + +as a+1 bs b+1 +0 0+d ，分别有⎧⎡0 1 0 0 ⎤⎡⎤0⎪⎢0 0 1 0 ⎥⎥⎢⎥⎢⎥0⎪⎢⎪⎪x =⎢ ⎥x+⎢⎥ u ⑴能控标准型：⎨⎢0 0 0 1 ⎥⎥⎢⎥⎢⎥0⎪⎢⎪⎣⎢−a0 −a1 −a2 −a n−1⎥⎦⎢⎥⎣⎦1⎪⎪⎩y=[b0 b1 b n−2 b n−1]x du+⎧⎡0 0 0 −a0 ⎤⎡b0 ⎤⎪⎪⎢⎢1 0 0 −a1 ⎥⎥⎢⎢b1 ⎥⎥⎪⎪x =⎢0 1 0 −a2 ⎥⎥x+⎢⎢ ⎥⎥u⑵能观标准型：⎨⎢b n−2⎥⎪⎢ ⎥⎢⎪⎣⎢0 0 1 −a n−1⎦⎥⎢⎣b n−1⎥⎦⎪⎪⎩y=[0 0 0 1]x du+⎧⎡p1⎪⎢0⎪x =⎢⎢ 0 p20 0 ⎤⎡1⎤0 ⎥⎢1⎥⎥x+⎢⎥u ⎥⎢ ⎥⎪⑶对角线标准型：⎨⎪⎢⎣0⎪p n⎥⎦⎢⎣1⎥⎦⎪⎩y=[c1 c2 c x du n] + 式中的pp1, 2,, p n和c c1, 2,, c n可由下式给出，G s( )= b s n−s1nn−1a s+n−b s1n−n2−1n+−2 + +as a+1 bs b+1 +0 0 + =d s p−c1 1 + s p−c2 2 + + s p−c n n +d+能控标准型的特点：状态矩阵的最后一行由传递函数的分母多项式系数确定，其余部分具有特定结构，输出矩阵依赖于分子多项式系数，输入矩阵中的元素除了最后一个元素是1 外，其余全为0。

第1章绪论1.1 控制系统的构成控制系统的组成和运行的普遍机制是控制论的反馈控制原理。

从信息处理和控制的角度看，控制系统可以看成由施控系统和被控系统两部分组成，并运行于一定的扰动和环境中，如图1–1所示。

施控系统产生控制作用，控制被控系统的物质流、能量流、信息流和资金流在规定的条件下以期望的或最优的方式运行。

扰动图1–1 控制系统的组成施控系统和被控系统的划分应根据实际应用情况定，由所考察的重点确定。

被控系统包括单台机械或设备、生产线、生产过程、以及整个工厂和企业等，它们是接受物质流、能量流、信息流和资金流的对象，也称控制对象。

施控系统应包括传感、控制和执行三部分。

传感是获得被控系统的状态、输出和环境等方面信息的各种手段之总和，包括测量物理变量的传感器，为获得某些不能用测量仪表测量的变量的软测量技术，以及多传感器信息融合技术等。

执行是产生施控系统最终输出信息的各种手段之总和，它可能是驱动部件（如调节阀、电动机、继电器等）、信息转换和通信部件（如与下级计算机的接口）、显示、记录以及图、文、声、多媒体输出部件等。

控制则以计算机为主体，完成控制问题的求解，形成控制算法和控制策略，产生控制规律，它是控制系统的核心。

抽象化后的控制系统结构如图1–2所示。

图1–2 控制系统结构当着重研究控制策略而不关心信息的获取以及控制输出的实现时，将传感简化为求差器，将控制、执行合称控制器，如图1–3所示。

控制策略（狭义也称控制算法）是控制器的核心，是控制理论研究的重点。

图1–3 简化的控制系统1.2 控制理论发展简况在工业应用和理论研究中，控制理论的发展过程大体上可分为三个阶段：经典控制理论、现代控制理论及智能控制理论。

这种阶段性的发展过程是由简单到复杂、由量变到质变的辩证发展过程，是现代科学技术迅速发展对自动控制的程度、精度、范围及其适应能力的需求越来越高，从而推动控制理论发展的结果。

理论来源于实践，反过来指导实践，控制理论的发展过程证明了这个真理。

《现代控制理论》课后习题及答案第一章控制系统的状态空间表达式1-1.试求图1-1系统的模拟结构图，并建立其状态空间表达式。

图1-27系统方块结构图图1-1 系统结构方块图解：系统的模拟结构图如下：图1-30双输入--双输出系统模拟结构图图1-2 双输入—双输出系统模拟结构图系统的状态方程如下：u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••6543211654321111111126543210000010000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2.有电路如图1-3所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

U图1-28 电路图图1-3 电路图解：由图，令32211,,x u x i x i c===，输出量22x R y =有电路原理可知：•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。

现代控制理论Model Control Theory前言1.胚胎萌芽期（1945年以前）•十八世纪以后，蒸汽机的使用提出了调速稳定等问题1765年俄国人波尔祖诺夫发明了锅炉水位调节器1784年英国人瓦特发明了调速器，蒸汽机离心式调速器1877年产生了劳斯稳定判据•十九世纪前半叶，动力使用了发电机、电动机促进了水利、水电站的遥控和程控的发展以及电压、电流的自动调节技术的发展•十九世纪末，二十世纪初，使用内燃机促进了飞机、汽车、船舶、机器制造业和石油工业的发展，产生了伺服控制和过程控制•二十世纪初第二次世界大战，军事工业发展很快飞机、雷达、火炮上的伺服机构，总结了自动调节技术及反馈放大器技术，搭起了经典控制理论的架子，但还没有形成学科。

2.经典控制理论时期（1940-1960）1945年美国贝尔实验室的Bode和Nyqusit提出频率响应法，奠定了控制理论的基础。

美国MIT的N. Wiener在研究随机过程的预测问题中，提出Wiener滤波理论.50年代趋于成熟.主要内容对单输入单输出系统进行分析，采用时域、频率法（频域）、根轨迹法（复数域）、相平面法、描述函数法；讨论系统稳定性的代数和几何判据以及校正网络等。

面临的挑战：被控对象日益复杂化、控制性能要求不断提高。

wiener3.现代控制理论时期（50年代末-60年代初）空间技术的发展提出了许多复杂控制问题，用于导弹、人造卫星和宇宙飞船上。

取得的成就1：1957年发射人造地球卫星；2：工业机器人产品；3：1961年载人航天；4：1969年登月；4.大系统和智能控制时期（70年代）各学科相互渗透，要分析的系统越来越大，越来越复杂。

例如：人工智能、模拟人的人脑功能、机器人等。

应用举例本课程内容•状态空间模型；•基于状态空间模型的系统分析（Analysis）：运动分析、能控性、能观性、稳定性•基于状态空间模型的系统综合（Synthesis）：极点配置、控制器设计、观测器设计、最优控制器设计。

（完整版）现代控制理论第⼀章线性离散系统第⼀节概述随着微电⼦技术，计算机技术和⽹络技术的发展，采样系统和数字控制系统得到⼴泛的应⽤。

通常把采样系统，数字控制系统统称为离散系统。

⼀、举例⾃动测温，控温系统图;加热⽓体图解：1. 当炉温h变化时，测温电阻R变化→R，电桥失去平衡状态，检流计指针发⽣偏转，其偏转⾓度为)e；(t2. 检流计是个⾼灵敏度的元件，为防磨损不允许有摩擦⼒。

当凸轮转动使指针）,接触时间为τ秒；与电位器相接触（凸轮每转的时间为T样偏差)(t e 是连续信号，电位器的输出的e *τ(t)是脉冲信号。

连续信号转变为脉冲信号的过程，成为采样或采样过程。

实现采样的装置成为采样器。

To —采样周期，f s =--To1采样频率，W s =2πf s —采样⾓频率 2．信号复现因接触时间很⼩，τo T ??τ，故可把采样器的输出信号）（t e *近似看成是⼀串强度等于矩形脉冲⾯积的理想脉冲，为了去除采样本⾝带来的⾼额分量，需要把离散信号）（t e *恢复到原信号)(t e 。

实现⽅法：是在采样器之后串联⼀个保持器，及信号复现滤波器。

作⽤：是把）（t e *脉冲信号变成阶梯信号e h (t)3.采样系统结构图r(t)，e(t)，c(t)，y(t)为连续信号，）（t e *为离散信号)(s G h ，)(s G p ，)(s H 分别为保持器，被控对象和反馈环节的传递函数。

(t)r4.采样系统⼯作过程由保持器5. 采样控制⽅式采样周期To ??=≠=?相位不同步采样常数常数6. 采样系统的研究⽅法（或称使⽤的数字⼯具）因运算过程中出现s 的超越函数，故不⽤拉式变换法，⼆采⽤z 变换⽅法，状态空间法。

第⼆节信号的采样和复现第⼀节是定性认识与分析，本节是定量研究。

⼀、采样过程从第3个图形可知，采样器输出信号）（t e *是⼀串理想的脉冲信号，k 瞬时）（t e *的脉冲强度等于此时)(T e 的幅值)(0kT e ，即)0(0T e ，)(0T e ，)2(0T e …. )(0nT e ….采样过程可以看成为⼀个幅值调制过程，采样器如同⼀个幅值调制器。