2020高考文科数学(人教版)一轮复习讲义：第1讲 集合的概念与运算 含答案

2020年高考数学一轮复习第一章第1节集合题组一集合的差不多概念1.(2018·广东高考)全集U＝R，集合M＝{x|－2≤x－1≤2}和N＝{x|x＝2k－1，k ＝1,2，…}的关系的韦恩(Venn)图如图所示，那么阴影部分所示的集合的元素共有()A.2个B.3个C.1个D.无穷多个解析：M＝{x|－1≤x≤3}，N＝{x|x＝2k－1，k ∈N*}，∴M∩N＝{1,3}.答案：A2.集合A＝{a，b,2}，B＝{2，b2,2a}，那么A∩B＝A∪B，那么a＝.解析：由A∩B＝A∪B知A＝B，又依照集合元素的互异性，因此有222a bb aa b⎧=⎪=⎨⎪≠≠⎩或222a bb aa b⎧=⎪=⎨⎪≠≠⎩，解得1ab=⎧⎨=⎩或1412ab⎧=⎪⎪⎨⎪=⎪⎩故a＝0或14答案：0或14题组二集合间的差不多关系3.全集U＝R(Venn)图是()解析：∵M＝{－1,0,1}，N＝{0，－1}，∴N M.答案：B4.集合A＝{x|x2＋x－6＝0}，B＝{x|mx＋1＝0}，假设B A，那么实数m的取值集合是()A.{－12，0，} B.{0,1} C.{－12，13} D.{0}解析：由x2＋x－6＝0得x＝2或x＝－3，∴A ＝{2，－3}.又∵B A ，∴当m ＝0时，B ＝∅，满足条件；当m ≠0时，B ＝{－1m }，∴－1m ＝2或－1m＝－3， 即m ＝－12或m ＝13. 答案：A5.(2018·江苏高考)集合A ＝{x |log 2x ≤2}，B ＝(－∞，a )，假设A ⊆B ，那么实数a 的取值范畴是(c ，＋∞)，其中c ＝ .解析：A ＝{x |0<x ≤4}，B ＝(－∞，a ).假设A ⊆B ，那么a >4.即a 的取值范畴为(4，＋∞)，∴c ＝4.答案：4题组三 集合的差不多运算6.(2018·山东高考)a 的值为( )A.0B.1C.2D.4解析：∵A ∪B ＝{0,1,2，a ，a 2}，又A ∪B ＝{0,1,2,4,16}，∴{a ，a 2}＝{4,16}，∴a ＝4.答案：D7.(2018·东北师大附中模拟)设全集U 是实数集R ，M ＝{x |x 2＞4}，N ＝{x |x ≥3或x ＜1}差不多上U 的子集，那么图中阴影部分所表示的集合是 ( )A.{x |－2≤x ＜1}B.{x |－2≤x ≤2}C.{x |1＜x ≤2}D.{x |x ＜2}解析：图中阴影部分表示N ∩(∁U M )，∵M ＝{|x 2>4}＝{x |x >2或x <－2}∴∁U M ＝{x |－2≤x ≤2}，∴N ∩(∁U M )＝{－2≤x ＜1}.答案：A8.(文)假设集合A ＝{x |(2x ＋1)(x －3)＜0}，B ＝{x ∈N *|x ≤5}，那么A ∩B 是 ( )A.{1,2,3}B.{1,2}C.{4,5}D.{1,2,3,4,5}解析：A ＝{x |－12＜x ＜3}，B ＝{1,2,3,4,5}， ∴A ∩B ＝{1,2}.答案：B(理)假设集合A ＝{x ||2x －1|<3}，B ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ 2x ＋13－x <0，那么A ∩B 是 ( ) A.⎩⎨⎧⎭⎬⎫x ⎪⎪－1<x <－12或2<x <3 B.{x |2<x <3}C.⎩⎨⎧⎭⎬⎫x ⎪⎪ －12<x <2 D.⎩⎨⎧⎭⎬⎫x ⎪⎪－1<x <－12 解析：∵A ＝{x |－2＜2x ＜4}＝{x |－1＜x ＜2}，B ＝{x |(2x ＋1)(x －3)＞0}＝{x |x ＞3或x ＜－12}， ∴A ∩B ＝{x |－1＜x ＜－12}. 答案：D题组四 集合的综合应用9.(2018·江西高考)U U A ∩B 非空，那么A ∩B 的元素个数为 ( )A.mnB.m ＋nC.n － mD.m －n解析：如图，U ＝A ∪B 中有m 个元素，∵(∁U A )∪(∁U B )＝∁U (A ∩B )中有n 个元素，∴A ∩B 中有m －n 个元素.答案：D10.设全集U ＝A ∪B ＝{x ∈N *|lg x ＜1}.假设A ∩(∁U B )＝{m |m ＝2n ＋1，n ＝0,1,2,3,4}，那么集合B ＝ .解析：∵lg x ＜1，∴0＜x ＜10.又∵x ∈N *，∴U ＝A ∪B ＝{1,2,3，…，9}.又∵A ∩(∁U B )＝{1,3,5,7,9}，∴B＝{2,4,6,8}.答案：{2,4,6,8}11.(文)(2018·北京高考)设A是整数集的一个非空子集.关于k∈A，假如k－1∉A，且k＋1∉A，那么称k是A的一个〝孤立元〞.给定S＝{1,2,3,4,5,6,7,8}，由S的3个元素构成的所有集合中，不含〝孤立元〞的集合共有个.解析：依题可知，由S的3个元素构成的所有集合中，不含〝孤立元〞，这三个元素一定是相连的三个数.故如此的集合共有6个.答案：6(理)对任意两个集合M、N，定义：M－N＝{x|x∈M且x∉N}，M*N＝(M－N)∪(N－M)，设M＝{y|y ＝x2，x∈R}，N＝{y|y＝3sin x，x∈R}，那么M*N＝.解析：依题意有M＝[0，＋∞)，N＝[－3,3]，因此M－N＝(3，＋∞)，N－M＝[－3,0)，故M*N＝(M－N)∪(N－M)＝[－3,0)∪(3，＋∞).答案：[－3,0)∪(3，＋∞)12.设A＝{x|x2－ax＋a2－19＝0}，B＝{x|x2－5x＋6＝0}，C＝{x|x2＋2x－8＝0}.(1)A∩B＝A∪B，求a的值；(2)∅A∩B，且A∩C＝∅，求a的值；(3)A∩B＝A∩C≠∅，求a的值.解：(1)因为A∩B＝A∪B，因此A＝B，又由对应系数相等可得a＝5和a2－19＝6同时成立，即a ＝5.(2)由于B＝{2,3}，C＝{－4,2}，且∅A∩B，A∩C＝∅，故只可能3∈A.现在a2－3a－10＝0，即a＝5或a＝－2，由(1)可知，当a＝5时，A＝B＝{2,3}，现在A∩C≠∅，与矛盾，因此a＝5舍去，故a＝－2.(3)由于B＝{2,3}，C＝{－4,2}，且A∩B＝A∩C≠∅，现在只可能2∈A，即a2－2a－15＝0，也即a＝5或a＝－3，由(2)可知a＝5不合题意，故a＝－3.。

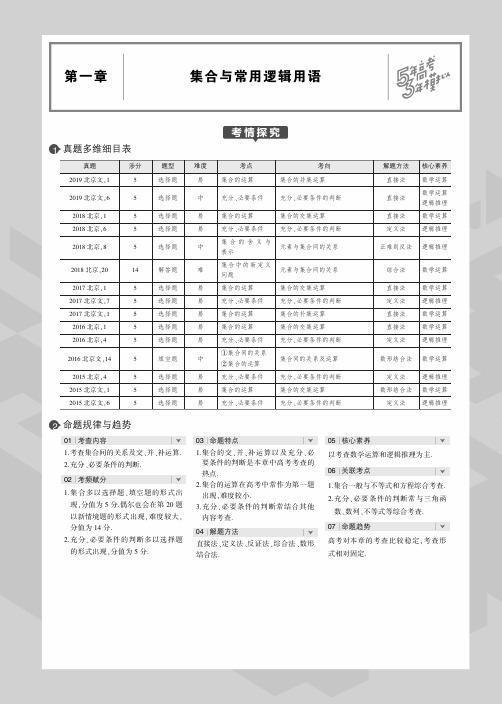
第一章 集合与常用逻辑用语第一节集 合2019考纲考题考情考编荽求考劭举例考向掠签耕與含的含重+兀累与集告的训于孟 慕1轻用叫幣法或搞建注挖*怙合蛋越昔帕了篥宅了杆电血耳空越的舍宝 井会拿井Venn(卞战)罔夜込if.合的Jt 黍与运算却厨・Of 耳总I - T 『荣件的补如皿•全号欖n 畢a 的義系方臨｝曲』占*全N^llt * T,tJ&合的空tfc 込謀) Ml 了*牝科卷I - Tifft 合的交*井适算) 別】7 •全国趙U ・TJ 卑合的幷黒运真＞】.集台的需文歴左小2.集售间的壯眾羌乘乳事令的运算橙心當導■放学远博.数为抽魚1. 集合的含义与表示方法 (1)集合的含义：研究对象叫做元素，一些元素组成的总体叫做集合。

集合中元素的性质：确定性、无序性、互异性。

(2) 元素与集合的关系：①属于，记为殳；②不属于，记为？。

(3) 集合的表示方法：列举法、描述法和图示法。

(4) 常用数集的记法：自然数集 N ，正整数集N *或N +,整数 集Z ,有理数集Q ,实数集R 。

2. 集合间的基本关系微知识•小題练-基础微械理-知识必备"国报革 丄JICHU W£]SHL.1J I3•集合的基本运算•常记结论•1. 集合元素的三个特性确定性、无序性、互异性。

2. 集合的子集个数若有限集A中有n个元素，则A的子集有2n个，非空子集有2n- 1个，真子集有2n- 1个。

3. 注意空集空集是任何集合的子集，是任何非空集合的真子集，应时刻关注对空集的讨论，防止漏解4.集合的运算性质 (1)并集的性质： A U ? = A ; A U A = A ; A U 3= B U A ; ALB = A? B? A(2)交集的性质：A n ?=?； A n A = A ； A nB = B n A ； A n B=A? A? B(3)补集的性质：A U ?u A) = U ; A n (?U A)= ?; ?U (?U A) = A o ?u(A n B) = (?u A )q ?u B)； ?U (ALB)= (?u A)Q (?u B)。

专题01 集合的含义及运算一、本专题要特别小心：1.元素与集合，集合与集合关系混淆陷阱；2.造成集合中元素重复陷阱；3.隐含条件陷阱；4.代表元变化陷阱；5.分类讨论陷阱；6．子集中忽视空集陷阱；7.新定义问题；8.任意、存在问题中的最值陷阱.二、【学习目标】1．了解集合的含义、元素与集合的“属于”关系，能用自然语言、图形语言、集合语言(列举法或描述法)来描述不同的具体问题，理解集合中元素的互异性；2．理解集合之间包含和相等的含义，能识别给定集合的子集，了解在具体情境中全集与空集的含义；3．理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集，理解在给定集合中一个子集的补集的含义，会求给定子集的补集；4．能使用韦恩(V enn)图表达集合间的关系与运算．三、【知识要点】1．集合的含义与表示(1)一般地，我们把研究对象统称为元素，把一些元素组成的总体叫集合，简称集．(2)集合中的元素的三个特征：确定性、互异性、无序性．(3)集合的表示方法有：描述法、列举法、区间法、图示法．(4)集合中元素与集合的关系分为属于与不属于两种，分别用“∈”或“∉”来表示．(5)常用的数集：自然数集N；正整数集N*(或N＋)；整数集Z；有理数集Q；实数集R.2．集合之间的关系(1)一般地，对于两个集合A，B.如果集合A的任何一个元素都是集合B的元素，我们就说这两个集合有包含关系，称集合A为集合B的子集，记作A⊆B；若A⊆B，且A≠B，，我们就说A是B的真子集．(2)不含任何元素的集合叫做空集，记作φ，它是任何一个集合的子集，是任何一个非空集合的真子集。

3．集合的基本运算(1)并集：A∪B＝{x|x∈A或x∈B}；(2)交集：A∩B＝{x|x∈A且x∈B}；(3)补集：∁U A＝．4．集合的运算性质(1)A∩B＝A⇔A⊆B，A∩A＝A，A∩∅＝∅；(2)A∪B＝A⇔A⊇B，A∪A＝A，A∪∅＝A；(3)A⊆B，B⊆C，则A⊆C；(4)∁U(A∩B)＝∁U A∪∁U B，∁U(A∪B)＝∁U A∩∁U B，A∩∁U A＝∅，A∪∁U A＝U，∁U(∁U A)＝A；(5)A⊆B，B⊆A，则A＝B.四．题型方法规律总结（一）集合的含义与表示例1．已知集合，则中元素的个数为A．9 B．8 C．5 D．4【答案】A【解析】，当时，；当时，；当时，；所以共有9个，选A.练习1．给出下列四个关系式：(1)；（2）；（3）；（4），其中正确的个数是（）A．1 B．2 C．3 D．4【答案】B【解析】（1）R为实数集，为实数，所以正确；（2）Z、Q分别为两个集合，集合间不能用属于符号，所以错误；（3）空集中没有任何元素，所以错误；（4）空集为任何集合的子集，所以正确.故选B.练习2．若A={1,2},B={(x,y)|x∈A,y∈A},则集合B中元素的个数为()A．1 B．2 C．3 D．4【答案】D【解析】由题意得集合，所以集合B中共有4个元素．故选D．（二）集合中代表元易错点揭秘例2．已知集合A满足条件:若a∈A,则∈A,那么集合A中所有元素的乘积为() A．-1 B．1 C．0 D．±1【答案】B【解析】由题意，当时，，令代入，则，则，则，即，所以，故选B.练习1．若集合A＝｛x｜mx2＋2x＋m＝0，m∈R｝中有且只有一个元素，则m的取值集合是A．｛1｝B．｛｝C．｛0，1｝D．｛，0，1｝【答案】D【解析】时，，满足题意；时，，．综上的取值集合是．练习2．用列举法表示集合＝________．【答案】{－11，－6，－3，－2，0，1，4，9}.【解析】，为的因数则则答案为练习3．集合{|y y ∈N =用列举法可表示为__________.【答案】{}1,2,4,8 【解析】∵,1x x ∈≠N ,∴当0x =时, 8y =-,不符合题意, 当2x =时, 8y =,符合题意, 当3x =时, 4y =,符合题意, 当4x =时, 83y =,不符合题意, 当5x =时, 2y =,符合题意,当6x =时, 85y =,不符合题意, 当7x =时, 86y =,不符合题意,当8x =时, 87y =,不符合题意,当9x =时, 1y =,符合题意,则y =，不符合题意.∴用列举法可表示为{}1,2,4,8. （三）集合的基本关系 例3．已知集合，，若，则实数的取值集合为（ ）A ．B ．C ．D ．【答案】D【解析】∵集合M={x|x 2=1}={﹣1，1}，N={x|ax=1}，N ⊆M ，∴当a=0时，N=∅，成立； 当a≠0时，N={}， ∵N ⊆M ，∴或=1．解得a=﹣1或a=1，综上，实数a 的取值集合为{1，﹣1，0}．故选：D．练习1．已知集合，，则的真子集的个数为（）A．3 B．4 C．7 D．8【答案】C【解析】由题意得，，∴，∴的真子集的个数为个．故选C．练习2．若函数在区间内没有最值,则的取值范围是（）A．B．C．D．【答案】B【解析】函数的单调区间为，由，得．∵函数在区间内没有最值，∴函数在区间内单调，∴，∴，解得．由，得．当时，得；当时，得，又，故．综上得的取值范围是．故选B．练习3.已知集合，，若，则实数的取值范围是( ) A．B．C．D．【答案】A【解析】由已知得，由，则，又，所以.故选A.（四）子集中常见错误例4. 已知集合,,若,则实数的取值范围是( )A．B．C．D．【答案】C【解析】当集合时，，解得，此时满足；当，即时，应有：，据此可得：，则，综上可得：实数的取值范围是.本题选择C选项.练习1．Z(M)表示集合M的子集个数，设集合A=，B=，则= A．3 B．4 C．5 D．7【答案】B【解析】；B=∴；集合的子集有：∴Z（A∩B）＝4．故选：B练习2.设集合，不等式的解集为B.（Ⅰ）当时，求集合A,B；（Ⅱ）当，求实数的取值范围.【答案】(Ⅰ)，；(Ⅱ)或.【解析】（Ⅰ）当时，，.（Ⅱ）①若，即时，可得， 满足，故符合题意．②当时，由，可得，且等号不能同时成立， 解得． 综上可得或．∴实数的取值范围是．练习3．设全集U=R ，集合A={x|1≤x ＜4}，B={x|2a≤x ＜3-a}．（1）若a=-2，求B∩A ，B∩(∁U A)；（2）若A ∪B=A ，求实数a 的取值范围． 【答案】（1）B ∩A =[1，4），B ∩(∁U A )= [-4,1)∪[4,5)；（2） .【解析】（1）∵A ={x |1≤x ＜4}，∴∁U A ={x |x ＜1或x ≥4}，∵B ={x |2a ≤x ＜3-a }，∴a =-2时，B ={-4≤x ＜5}，所以B ∩A =[1，4）， B ∩(∁U A )={x |-4≤x ＜1或4≤x ＜5}=[-4,1)∪[4,5). （2）A ∪B =A ⇔B ⊆A ， ①B =∅时，则有2a ≥3-a ，∴a ≥1, ②B ≠∅时，则有，∴,综上所述，所求a 的取值范围为.（五）集合的基本运算 例5.已知，，则()R AB ð中的元素个数为（ ）A ．1B ．2C ．6D ．8【答案】B【解析】解：{1x x =<，或3}x ≥，，，的元素个数为2个.故选:B .练习1．已知集合，，若A B A ⋂=，则实数a 的取值范围是( )A ．(],3-∞-B ．(),3-∞-C ．(],0-∞D ．[)3,+∞ 【答案】A【解析】由已知得[]3,3A =-，由A B A ⋂=，则A B ⊆，又[),B a =+∞，所以3a ≤-.故选A.练习2．集合，,若，则的取值范围是（ ）A ．B ．C ．D ．【答案】B 【解析】根据题意，可得，，要使，则，故选B.练习3．设全集是实数集，，则图中阴影部分所表示的集合是________.【答案】【解析】∵，∴， ∴．（六）集合的应用例6．学校先举办了一次田径运动会，某班共有8名同学参赛，又举办了一次球类运动会，这个班有12名同学参赛，两次运动会都参赛的有3人.两次运动会中，这个班总共的参赛人数为（ ） A ．20 B ．17C ．14D ．23【答案】B【解析】因为参加田径运动会的有8名同学，参加球类运动会的有12名同学，两次运动会都参加的有3人，所以两次运动会中，这个班总共的参赛人数为.故选B练习1．已知集合.给定一个函数，定义集合若对任意的成立，则称该函数具有性质“”(I)具有性质“”的一个一次函数的解析式可以是_____；(Ⅱ)给出下列函数：①；②；③，其中具有性质“”的函数的序号是____．（写出所有正确答案的序号）【答案】（答案不唯一）①②【解析】(I)对于解析式：，因为，，…符合。

2020年第一轮高考数学专题复习第一讲：集合一、考纲导读（一）集合的含义与表示1．了解集合的含义、元素与集合的“属于”关系.2．能用自然语言、图形语言、集合语言（列举法或描述法）描述不同的具体问题。

（二）集合间的基本关系1．理解集合之间包含与相等的含义，能识别给定集合的子集.2．在具体情境中，了解全集与空集的含义.（三）集合的基本运算1．理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集。

2．理解在给定集合中一个子集的补集的含义，会求给定子集的补集.3．能使用韦恩图（Venn）表达集合的关系及运算。

根据考试大纲的要求，结合2009年高考的命题情况，我们可以预测2010年集合部分在选择、填空和解答题中都有涉及，高考命题热点有以下两个方面：一是集合的运算、集合的有关述语和符号、集合的简单应用等作基础性的考查，题型多以选择、填空题的形式出现；二是以函数、方程、三角、不等式等知识为载体，以集合的语言和符号为表现形式，结合简易逻辑知识考查学生的数学思想、数学方法和数学能力，题型常以解答题的形式出现.第1课时 集合的概念一、基础过关 <1>.集合1．集合是一个不能定义的原始概念，描述性定义为：某些指定的对象 就成为一个集合，简称 ．集合中的每一个对象叫做这个集合的 ．2．集合中的元素属性具有：(1) 确定性； (2) ； (3) ．3．集合的表示法常用的有 、 和韦恩图法三种，有限集常用 ，无限集常用 ，图示法常用于表示集合之间的相互关系．<2>.元素与集合的关系4．元素与集合是属于和 的从属关系，若a 是集合A 的元素，记作 ，若a 不是集合B 的元素，记作 ．但是要注意元素与集合是相对而言的．<3>.集合与集合的关系5．集合与集合的关系用符号 表示．6．子集：若集合A 中 都是集合B 的元素，就说集合A 包含于集合B （或集合B 包含集合A ），记作 ．7．相等：若集合A 中 都是集合B 的元素，同时集合B 中 都是集合A 的元素，就说集合A 等于集合B ，记作 ．8．真子集：如果 就说集合A 是集合B 的真子集，记作 ．9．若集合A 含有n 个元素，则A 的子集有 个，真子集有 个，非空真子集有 个．10．空集∅是一个特殊而又重要的集合，它不含任何元素，∅是任何集合的 ，∅是任何非空集合的 ，解题时不可忽视∅．二、典型例题例1. 已知集合8|6A x N N x ⎧⎫=∈∈⎨⎬-⎩⎭，试求集合A 的所有子集.变式训练1.若a,b ∈R,集合{}1,,0,,,b a b a b a ⎧⎫+=⎨⎬⎩⎭求b-a 的值.例2. 设集合2{2,3,23}U a a =+-，{|21|,2}A a =-，{5}U C A =，求实数a 的值.变式训练2：（1）P ＝{x|x2－2x －3＝0}，S ＝{x|ax ＋2＝0}，S ⊆P ，求a 取值？（2）A ＝{－2≤x ≤5}，B ＝{x|m ＋1≤x ≤2m －1}，B ⊆A,求m 。

第1讲集合的概念与运算[考纲解读] 1.了解集合的含义．体会元素与集合的关系，能用自然语言、图形语言、集合语言(列举法或描述法)描述具体问题．2.理解集合间的相等与包含关系，会求集合的子集，了解全集与空集的含义．(重点)3.在理解集合间的交、并、补的含义的基础上，会求两个集合的并集与交集，会求给定子集的补集．(重点、难点)4.能使用Venn图表达集合间的基本关系及基本运算．[考向预测] 从近三年高考情况来看，本讲一直是高考中的热点．预测2020年高考会以考查集合交、并、补的运算为主，结合不等式的解法，求函数的定义域、值域等简单综合命题，试题难度不大，以选择题形式呈现.1．集合与元素02互异性、□03无序性．(1)集合中元素的三个特征：□01确定性、□07∉表示．(2)元素与集合的关系有□04属于或□05不属于两种，用符号□06∈或□09描述法、□10图示法．(3)集合的表示法：□08列举法、□(4)常见数集的记法2．集合间的基本关系3．集合的基本运算4．集合的运算性质(1)并集的性质：A ∪∅＝A ；A ∪A ＝A ；A ∪B ＝B ∪A ；A ∪B ＝A ⇔□01B ⊆A . (2)交集的性质：A ∩∅＝∅；A ∩A ＝A ；A ∩B ＝B ∩A ；A ∩B ＝A ⇔□02A ⊆B . (3)补集的性质：A ∪(∁U A )＝□03U ；A ∩(∁U A )＝□04∅；∁U (∁U A )＝□05A ；∁U (A ∪B )＝(∁U A )∩(∁UB )；∁U (A ∩B )＝(∁U A )∪(∁U B )．(4)若有限集A 中有n 个元素，则A 的子集个数为□062n 个，非空子集个数为□072n －1个，真子集有□082n －1个，非空真子集的个数为□092n －2个．1．概念辨析(1)若1∈{x ，x 2}，则x ＝±1.( )(2){x |y ＝x 2}＝{y |y ＝x 2}＝{(x ，y )|y ＝x 2}．( ) (3){x |x ≥2}＝{t |t ≥2}．( )(4)对于任意两个集合A ，B ，总有(A ∩B )⊆A ，A ⊆(A ∪B )．( ) 答案 (1)× (2)× (3)√ (4)√2．小题热身(1)若集合A ＝{x |－2<x <1}，B ＝{x |x <－1或x >3}，则A ∩B ＝( ) A ．{x |－2<x <－1} B ．{x |－2<x <3} C ．{x |－1<x <1} D ．{x |1<x <3}答案 A解析 A ∩B ＝{x |－2<x <－1}．(2)设全集U ＝{x |x ∈N *，x <6}，集合A ＝{1,3}，B ＝{3,5}，则∁U (A ∪B )等于( ) A ．{1,4} B ．{1,5} C ．{2,5} D ．{2,4} 答案 D解析 ∵U ＝{1,2,3,4,5}，A ∪B ＝{1,3,5}，∴∁U (A ∪B )＝{2,4}． (3)已知集合A ＝{1,3，m }，B ＝{1，m }，若B ⊆A ，则m ＝________. 答案 0或3解析 ∵A ＝{1,3，m }，B ＝{1，m }，B ⊆A ， ∴m ＝3或m ＝m ，∴m ＝3或0或1，经检验m ＝0或3.(4)已知集合A ＝⎩⎨⎧⎭⎬⎫8x ，y ，B ＝{0，x 2}，且A ＝B ，则集合A 的子集为________． 答案 ∅，{0}，{4}，{0,4}解析 由题意得8x＝x 2，y ＝0，解得x ＝2，所以A ＝{0,4}，其子集为∅，{0}，{4}，{0,4}．题型 一 集合的基本概念1．若集合A ＝{x ∈R |ax 2－3x ＋2＝0}中只有一个元素，则a 等于( ) A.92 B.98 C ．0 D ．0或98 答案 D解析 当a ＝0时，A ＝⎩⎨⎧⎭⎬⎫23，符合题意；当a ≠0时，Δ＝(－3)2－4×a ×2＝0，解得a ＝98，此时A ＝⎩⎨⎧⎭⎬⎫43，符合题意．综上知a ＝0或98.2．(2018·全国卷Ⅱ)已知集合A ＝{(x ，y )|x 2＋y 2≤3，x ∈Z ，y ∈Z }，则A 中元素的个数为( )A ．9B ．8C ．5D ．4 答案 A解析 ∵x 2＋y 2≤3，∴x 2≤3，∵x ∈Z ，∴x ＝－1,0,1，当x ＝－1时，y ＝－1,0,1；当x ＝0时，y ＝－1,0,1；当x ＝1时，y ＝－1,0,1，所以A 中元素共有9个，故选A.3．若集合A ＝{a －3,2a －1，a 2－4}，且－3∈A ，则实数a ＝________. 答案 0或1解析 因为－3∈A ，所以a －3＝－3或2a －1＝－3或a 2－4＝－3， 解得a ＝0或a ＝－1或a ＝1.当a ＝0时，A ＝{－3，－1，－4}，符合题意；当a ＝－1时，2a －1＝a 2－4＝－3，不满足集合中元素的互异性，故舍去； 当a ＝1时，A ＝{－2,1，－3}，符合题意． 综上知a ＝0或1.1．用描述法表示集合的两个关键点(1)搞清楚集合中的代表元素是什么．如举例说明1,3是数，举例说明2是有序数对(或平面内的点)．(2)看这些元素满足什么限制条件．如举例说明1，关于x 的方程只有一个实根．举例说明2，x ，y 是整数且满足x 2＋y 2≤3.2．两个易错点(1)忽视集合中元素的互异性．如举例说明3，求出a 值后应注意检验． (2)忽视分类讨论．如举例说明1，要分a ＝0与a ≠0两种情况讨论．1．设集合A ＝{0,1,2,3}，B ＝{x |－x ∈A,1－x ∉A }，则集合B 中元素的个数为( ) A ．1 B ．2 C ．3 D ．4 答案 A解析 若x ∈B ，则－x ∈A ，所以x 只可能取0，－1，－2，－3.逐一检验可知B ＝{－3}，只有1个元素．2．已知集合A ＝{x |x ＝3k －1，k ∈Z }，则下列表示正确的是( )A ．－1∉AB ．－11∈AC ．3k 2－1∈A D ．－34∉A答案 C解析 令k ＝0得x ＝－1，故－1∈A ； 令－11＝3k －1，解得k ＝－103∉Z ，故－11∉A ； 令－34＝3k －1，解得k ＝－11∈Z ，故－34∈A ； 对于3k 2－1，因为k ∈Z 时，k 2∈Z ， 所以3k 2－1∈A .所以C 项正确． 题型 二 集合间的基本关系1．已知a ，b ∈R ，若⎩⎨⎧⎭⎬⎫a ，b a ，1＝{a 2，a ＋b,0}，则a 2018＋b 2018为( ) A ．1 B ．0 C ．－1 D ．±1 答案 A解析 ∵⎩⎨⎧⎭⎬⎫a ，b a，1＝{a 2，a ＋b,0}，∴a ≠0.∴b ＝0，a 2＝1，又∵a ≠1，∴a ＝－1，∴a2018＋b2018＝1.2．已知集合M ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＝k π4＋π4，k ∈Z，集合N ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＝k π8－π4，k ∈Z，则( )A ．M NB ．N MC ．M ＝ND ．以上都不对答案 A 解析 ∵k π4＋π4＝k ＋8π，k ∈Z ，k π8－π4＝k －28π，k ∈Z ， ∴任取x ∈M ，有x ∈N ，且π8∈N ，但π8∉M ，∴MN .3．已知集合A ＝{x |－2≤x ≤5}，B ＝{x |m ＋1≤x ≤2m －1}，若B ⊆A ，则实数m 的取值范围为________．答案 (－∞，3]解析 因为B ⊆A ，所以①若B ＝∅，则2m －1<m ＋1，此时m <2. ②若B ≠∅，则⎩⎪⎨⎪⎧2m －1≥m ＋1，m ＋1≥－2，2m －1≤5.解得2≤m ≤3.由①②可得，符合题意的实数m 的取值范围为m ≤3.条件探究1 举例说明3中的集合B 改为“B ＝{x |m ≤x ≤m ＋1}”，其余不变，该如何求解？解 B ＝{x |m ≤x ≤m ＋1}≠∅，为使B ⊆A ，m 须满足⎩⎪⎨⎪⎧m ≥－2，m ＋1≤5，解得－2≤m ≤4.条件探究2 举例说明3中的集合A 改为“A ＝{x |x <－2或x >5}”，如何求解？ 解 因为B ⊆A ，所以①当B ＝∅时，即2m －1<m ＋1时，m <2，符合题意．②当B ≠∅时，⎩⎪⎨⎪⎧m ＋1≤2m －1，m ＋1>5或⎩⎪⎨⎪⎧m ＋1≤2m －1，2m －1<－2，解得⎩⎪⎨⎪⎧m ≥2，m >4或⎩⎪⎨⎪⎧m ≥2，m <－12，即m >4.综上可知，实数m 的取值范围为(－∞，2)∪(4，＋∞)．1．判断集合间关系的三种方法2．根据集合间的关系求参数的策略 (1)注意对集合是否为空集进行分类讨论因为∅⊆A 对任意集合A 都成立．如举例说明3中2m －1<m ＋1时，B ＝∅，B ⊆A 也成立． (2)借助Venn 图和数轴使抽象问题直观化．(3)注意检验区间端点值，如举例说明3，若将两个集合改为A ＝{x |－2<x ≤5}，B ＝{x |m＋1≤x <2m －1}，若B ≠∅，为使B ⊆A ，m 须满足⎩⎪⎨⎪⎧2m －1>m ＋1，m ＋1>－2，2m －1≤5.1．已知集合A ＝{x |x 2－3x ＋2＝0，x ∈R }，B ＝{x |0<x <5，x ∈N }，则( ) A ．B ⊆A B ．A ＝B C ．A B D ．B A 答案 C解析 由题意得A ＝{1,2}，B ＝{1,2,3,4}，∴AB .2．已知集合A ＝{x |x 2－2x ≤0}，B ＝{x |x ≤a }，若A ⊆B ，则实数a 的取值范围是( ) A ．a ≥2 B．a >2 C ．a <0 D ．a ≤0 答案 A解析 ∵A ＝{x |0≤x ≤2}，B ＝{x |x ≤a }，∴为使A ⊆B ，a 须满足a ≥2.3．满足A ⊆{0,1,2,3,4,5}的集合A 的个数为________．答案 7解析 集合A 除含元素0,1,2外，还至少含有3,4,5中的一个元素，所以集合A 的个数等于{3,4,5}的非空子集的个数，即为23－1＝7.题型 三 集合的基本运算角度1 集合的并、交、补运算1．(2018·天津高考)设集合A ＝{1,2,3,4}，B ＝{－1,0,2,3}，C ＝{x ∈R |－1≤x <2}，则(A ∪B )∩C ＝( )A ．{－1,1}B ．{0,1}C ．{－1,0,1}D ．{2,3,4}答案 C解析 因为集合A ＝{1,2,3,4}，B ＝{－1,0,2,3}，A ∪B ＝{－1,0,1,2,3,4}，所以(A ∪B )∩C ＝{－1,0,1}．2．(2018·皖北协作区联考)已知集合A ＝{y |y ＝x 2－1}，B ＝{x |y ＝lg (x －2x 2)}，则∁R (A ∩B )＝( )A.⎣⎢⎡⎭⎪⎫0，12 B ．(－∞，0)∪⎣⎢⎡⎭⎪⎫12，＋∞ C.⎝ ⎛⎭⎪⎫0，12 D ．(－∞，0]∪⎣⎢⎡⎭⎪⎫12，＋∞ 答案 D解析 因为A ＝{y |y ＝x 2－1}＝[0，＋∞)，B ＝{x |y ＝lg (x －2x 2)}＝⎝ ⎛⎭⎪⎫0，12，所以A ∩B ＝⎝ ⎛⎭⎪⎫0，12，所以∁R (A ∩B )＝(－∞，0]∪⎣⎢⎡⎭⎪⎫12，＋∞.角度2 知集合的运算结果求参数3．设U ＝R ，集合A ＝{x |x 2＋3x ＋2＝0}，B ＝{x |x 2＋(m ＋1)x ＋m ＝0}，若(∁U A )∩B ＝∅，则m ＝________.答案 1或2解析 A ＝{－2，－1}，由(∁U A )∩B ＝∅，得B ⊆A .x 2＋(m ＋1)x ＋m ＝0可化为(x ＋1)(x ＋m )＝0，当m ＝1时，B ＝{－1}，符合题意；当m ≠1时，B ＝{－1，－m }，为使B ⊆A 成立，须有－m ＝－2，即m ＝2. 综上知m ＝1或2.1．求集合交集、并集或补集的步骤2．知集合的运算结果求参数问题的两个关键点(1)分析运算结果并进行恰当转换．如举例说明3中，由(∁U A)∩B＝∅，知B⊆A.(2)化简集合为求参数创造有利条件．如举例说明3中，A＝{－2，－1}．当m＝1时，B＝{－1}；当m≠1时，B＝{－1，－m}．1．已知全集U＝R，集合M＝{x|(x－1)(x＋3)<0}，N＝{x||x|≤1}，则阴影部分(如图)表示的集合是( )A．[－1,1)B．(－3,1]C．(－∞，－3)∪[－1，＋∞)D．(－3，－1)答案 D解析由题意可知，M＝(－3,1)，N＝[－1,1]，所以阴影部分表示的集合为M∩(∁U N)＝(－3，－1)．2．(2018·全国卷Ⅰ)已知集合A＝{x|x2－x－2>0}，则∁R A＝( )A．{x|－1<x<2} B．{x|－1≤x≤2}C．{x|x<－1}∪{x|x>2} D．{x|x≤－1}∪{x|x≥2}答案 B解析解不等式x2－x－2>0得x<－1或x>2，所以A＝{x|x<－1或x>2}，所以∁R A＝{x|－1≤x≤2}，故选B.3．(2019·辽宁五校模拟)已知集合P＝{x|x2－2x－8>0}，Q＝{x|x≥a}，P∪Q＝R，则a 的取值范围是( )A ．(－2，＋∞)B ．(4，＋∞)C ．(－∞，－2]D ．(－∞，4]答案 C解析 集合P ＝{x |x 2－2x －8>0}＝{x |x <－2或x >4}，Q ＝{x |x ≥a }，若P ∪Q ＝R ，则a ≤－2，即a 的取值范围是(－∞，－2]．题型 四 集合的新定义问题已知集合M ＝{(x ，y )|y ＝f (x )}，若对于任意实数对(x 1，y 1)∈M ，都存在(x 2，y 2)∈M ，使得x 1x 2＋y 1y 2＝0成立，则称集合M 是“垂直对点集”．给出下列四个集合：①M ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ，y ⎪⎪⎪y ＝1x； ②M ＝{(x ，y )|y ＝log 2x }； ③M ＝{(x ，y )|y ＝e x－2}； ④M ＝{(x ，y )|y ＝sin x ＋1}． 其中是“垂直对点集”的序号是( ) A ．①④ B ．②③ C ．③④ D ．②④ 答案 C解析 记A (x 1，y 1)，B (x 2，y 2)，则由x 1x 2＋y 1y 2＝0得OA ⊥OB .对于①，对任意A ∈M ，不存在B ∈M ，使得OA ⊥OB .对于②，当A 为(1,0)时，不存在B ∈M 满足题意．对于③④，对任意A ∈M ，过原点O 可作直线OB ⊥OA ，它们都与函数y ＝e x－2及y ＝sin x ＋1的图象相交，即③④满足题意．与集合相关的新定义问题的解题思路(1)紧扣“新”定义：分析新定义的特点，把新定义所叙述的问题的本质弄清楚，并能够应用到具体的解题过程之中，这是破解新定义型集合问题的关键所在．(2)把握“新”性质：集合的性质(概念、元素的性质、运算性质等)是破解新定义型集合问题的基础，也是突破口，在解题时要善于从试题中发现可以使用集合性质的一些因素，在关键之处用好集合的性质．(3)遵守“新”法则：准确把握新定义的运算法则，将其转化为集合的交集、并集与补集的运算．如果集合A 满足：若x ∈A ，则－x ∈A ，那么就称集合A 为“对称集合”．已知集合A ＝{2x,0，x 2＋x }，且A 是对称集合，集合B 是自然数集，则A ∩B ＝________.答案 {0,6}解析 由题意可知－2x ＝x 2＋x ，所以x ＝0或x ＝－3.而当x ＝0时不符合元素的互异性，所以舍去．当x＝－3时，A＝{－6,0,6}，所以A∩B＝{0,6}．11。

§1.1高考数学第一轮复习讲义集合1．集合与元素(1)集合元素的三个特征：____________、______________、____________.(2)元素与集合的关系是________或__________关系，用符号______或______表示．(3)集合的表示法：____________、__________、__________、__________.(4)常用数集：自然数集N；正整数集N*(或N＋)；整数集Z；有理数集Q；实数集R.(5)集合的分类：按集合中元素个数划分，集合可以分为__________、__________、________.2．集合间的基本关系(1)子集、真子集及其性质对任意的x∈A，都有x∈B，则A⊆B(或B⊇A)．若A⊆B，且在B中至少有一个元素x∈B，但x∉A，则________(或________)．∅____A；A____A；A⊆B，B⊆C⇒A____C.若A含有n个元素，则A的子集有______个，A的非空子集有______个，A的非空真子集有______个．(2)集合相等若A⊆B且B⊆A，则A＝B.3．集合的运算及其性质(1)集合的交、并、补运算交集：A∩B＝________________；并集：A∪B＝{x|x∈A，或x∈B}；补集：∁U A＝________________.U为全集，∁U A表示A相对于全集U的补集．(2)集合的运算性质并集的性质：A∪∅＝A；A∪A＝A；A∪B＝B∪A；A∪B＝A⇔B⊆A.交集的性质：A∩∅＝∅；A∩A＝A；A∩B＝B∩A；A∩B＝A⇔A⊆B.补集的性质：A∪(∁U A)＝U；A∩(∁U A)＝∅；∁U(∁U A)＝A.[难点正本疑点清源]1．正确理解集合的概念正确理解集合的有关概念，特别是集合中元素的三个特征，尤其是“确定性和互异性”在解题中要注意运用．在解决含参数问题时，要注意检验，否则很可能会因为不满足“互异性”而导致结论错误． 2．注意空集的特殊性空集是不含任何元素的集合，空集是任何集合的子集．在解题时，若未明确说明集合非空时，要考虑到集合为空集的可能性．例如：A ⊆B ，则需考虑A ＝∅和A ≠∅两种可能的情况．3．正确区分∅，{0}，{∅}∅是不含任何元素的集合，即空集．{0}是含有一个元素0的集合，它不是空集，因为它有一个元素，这个元素是0.{∅}是含有一个元素∅的集合．∅⊆{0}，∅⊆{∅}，∅∈{∅}，{0}∩{∅}＝∅.1．(课本改编题)已知全集U ＝{1,2,3,4,5,6,7}，A ＝{2,4,5}，B ＝{1,3,5,7}，则A ∩(∁U B )＝________.2．若全集U ＝R ，集合A ＝{x |x ≥1}∪{x |x ≤0}，则∁U A ＝________.3．(课本改编题)已知集合A ＝{－1,2}，B ＝{x |mx ＋1＝0}，若A ∪B ＝A ，则m 的可能取值组成的集合为________．4．已知A 、B 均为集合U ＝{1,3,5,7,9}的子集，且A ∩B ＝{3}，(∁U B )∩A ＝{9}，则A 等于( ) A ．{1,3} B ．{3,7,9} C ．{3,5,9}D ．{3,9}5．已知R 是实数集，M ＝{x |2x <1}，N ＝{y |y ＝x －1}，则N ∩(∁R M )等于( )A ．(1,2)B ．[0,2]C ．∅D ．[1,2]题型一 集合的基本概念例1 (1)已知A ＝{a ＋2，(a ＋1)2，a 2＋3a ＋3}，且1∈A ，求实数2 013a 的值；(2)x ，x 2－x ，x 3－3x 能表示一个有三个元素的集合吗？如果能表示一个集合，说明理由；如果不能表示，则需要添加什么条件才能使它表示一个有三个元素的集合．探究提高 (1)加强对集合中元素的特征的理解，互异性常常容易忽略，求解问题时要特别注意．(2)分类讨论的思想方法常用于解决集合问题．若集合A ＝{x |ax 2－3x ＋2＝0}的子集只有两个，则实数a ＝________.题型二 集合间的基本关系例2 已知集合A ＝{x |0<ax ＋1≤5}，集合B ＝⎩⎨⎧⎭⎬⎫x |－12<x ≤2.(1)若A ⊆B ，求实数a 的取值范围；(2)若B⊆A，求实数a的取值范围；(3)A、B能否相等？若能，求出a的值；若不能，试说明理由．探究提高在解决两个数集关系问题时，避免出错的一个有效手段是合理运用数轴帮助分析与求解，另外，在解含有参数的不等式(或方程)时，要对参数进行分类讨论．分类时要遵循“不重不漏”的分类原则，然后对每一类情况都要给出问题的解答．分类讨论的一般步骤：①确定标准；②恰当分类；③逐类讨论；④归纳结论．已知集合A＝{x|log2x≤2}，B＝(－∞，a)，若A⊆B，则实数a的取值范围是(c，＋∞)，其中c＝________.题型三集合的基本运算例3设U＝R，集合A＝{x|x2＋3x＋2＝0}，B＝{x|x2＋(m＋1)x＋m＝0}．若(∁U A)∩B＝∅，则m的值是________．探究提高本题的主要难点有两个：一是集合A，B之间关系的确定；二是对集合B中方程的分类求解．集合的交并补运算和集合的包含关系存在着一些必然的联系，这些联系通过Venn图进行直观的分析不难找出来，如A∪B＝A⇔B⊆A，(∁U A)∩B＝∅⇔B⊆A 等，在解题中碰到这种情况时要善于转化，这是破解这类难点的一种极为有效的方法．设全集是实数集R，A＝{x|2x2－7x＋3≤0}，B＝{x|x2＋a<0}．(1)当a＝－4时，求A∩B和A∪B；(2)若(∁R A)∩B＝B，求实数a的取值范围．题型四集合中的新定义问题例4在集合{a，b，c，d}上定义两种运算和如下：那么d(a c)等于()A．a B．b C．c D．d探究提高本题新定义了两种运算，看似复杂，但事实上运算结果可以通过题目中的表格得出．借助于集合定义新运算是高考中命制创新试题的一个良好素材．已知集合S＝{0,1,2,3,4,5}，A是S的一个子集，当x∈A时，若有x－1∉A，且x＋1∉A，则称x为A的一个“孤立元素”，那么S中无“孤立元素”的4个元素的子集共有________个，其中的一个是____________．1.忽略空集致误试题：(1)(5分)若集合P＝{x|x2＋x－6＝0}，S＝{x|ax＋1＝0}，且S⊆P，则由a的可取值组成的集合为__________．(2)(5分)若集合A＝{x|－2≤x≤5}，B＝{x|m＋1≤x≤2m－1}，且B⊆A，则由m的可取值组成的集合为_____________________________________________________________．学生答案展示审题视角 (1)从集合的关系看，S ⊆P ，则S ＝∅或S ≠∅.(2)从集合元素看，第(1)小题S ≠∅时，S 中元素为－1a ＝－3或－1a ＝2，即a ＝13或a ＝－12.第(2)小题B ≠∅，必有⎩⎪⎨⎪⎧m ＋1≤2m －1m ＋1≥－22m －1≤5.正确答案 (1)⎩⎨⎧⎭⎬⎫0，13，－12 (2){m |m ≤3}解析 (1)P ＝{－3,2}．当a ＝0时，S ＝∅，满足S ⊆P ；当a ≠0时，方程ax ＋1＝0的解集为x ＝－1a，为满足S ⊆P 可使－1a ＝－3或－1a＝2，即a ＝13或a ＝－12.故所求集合为⎩⎨⎧⎭⎬⎫0，13，－12.(2)当m ＋1>2m －1，即m <2时，B ＝∅，满足B ⊆A ； 若B ≠∅，且满足B ⊆A ，如图所示，则⎩⎪⎨⎪⎧m ＋1≤2m －1，m ＋1≥－2，2m －1≤5，即⎩⎪⎨⎪⎧m ≥2，m ≥－3，m ≤3，∴2≤m ≤3.故m <2或2≤m ≤3，即所求集合为{m |m ≤3}．批阅笔记 本题考查的重点是集合间的关系及集合元素的特征．在解答本题时，存在两个突 出错误．一是忽略对∅的讨论．例如在(1)(2)需讨论S ＝∅和B ＝∅的情况；二是忽视对元素 的讨论，如(1)中，－1a ＝－3或－1a＝2两种情况.方法与技巧1．集合中的元素的三个特征，特别是无序性和互异性在解题时经常用到．解题后要进行检验，要重视符号语言与文字语言之间的相互转化．2．对连续数集间的运算，借助数轴的直观性，进行合理转化；对已知连续数集间的关系，求其中参数的取值范围时，要注意单独考察等号．3．对离散的数集间的运算，或抽象集合间的运算，可借助Venn 图．这是数形结合思想的又一体现． 失误与防范1．空集在解题时有特殊地位，它是任何集合的子集，是任何非空集合的真子集，时刻关注对空集的讨论，防止漏解．2．解题时注意区分两大关系：一是元素与集合的从属关系；二是集合与集合的包含关系．3．解答集合题目，认清集合元素的属性(是点集、数集或其他情形)和化简集合是正确求解的两个先决条件．4．Venn图示法和数轴图示法是进行集合交、并、补运算的常用方法，其中运用数轴图示法要特别注意端点是实心还是空心．5．要注意A⊆B、A∩B＝A、A∪B＝B、∁U A⊇∁U B、A∩(∁U B)＝∅这五个关系式的等价性．课时规范训练(时间：60分钟) A 组 专项基础训练题组一、选择题1．已知集合A ＝{(x ，y )|x ，y 为实数，且x 2＋y 2＝1}，B ＝{(x ，y )|x ，y 为实数，且y ＝x }，则A ∩B 的元素个数为( )A ．0B ．1C ．2D ．3 2．已知集合M ＝{x |xx －1≥0，x ∈R }，N ＝{y |y ＝3x 2＋1，x ∈R }，则M ∩N 等于 ( )A ．∅B ．{x |x ≥1}C ．{x |x >1}D ．{x |x ≥1或x <0}3．如果全集U ＝R ，A ＝{x |2<x ≤4}，B ＝{3,4}，则A ∩(∁U B )等于( )A ．(2,3)∪(3,4)B ．(2,4)C ．(2,3)∪(3,4]D ．(2,4]二、填空题4．已知集合A ＝{1,3，a }，B ＝{1，a 2－a ＋1}，且B ⊆A ，则a ＝__________.5．已知集合A ＝{(0,1)，(1,1)，(－1，2)}，B ＝{(x ，y )|x ＋y －1＝0，x ，y ∈Z }，则A ∩B ＝__________.6．定义集合运算：A ⊙B ＝{z |z ＝xy (x ＋y )，x ∈A ，y ∈B }，设集合A ＝{0,1}，B ＝{2,3}，则集合A ⊙B 的所有元素之和为________． 三、解答题7．已知集合A ＝{x |x 2－2x －3≤0}，B ＝{x |x 2－2mx ＋m 2－4≤0，x ∈R ，m ∈R }． (1)若A ∩B ＝[0,3]，求实数m 的值； (2)若A ⊆∁R B ，求实数m 的取值范围．8．对任意两个集合M 、N ，定义：M －N ＝{x |x ∈M 且x ∉N }，M *N ＝(M －N )∪(N －M )，设M ＝{y |y ＝x 2，x ∈R }，N ＝{y |y ＝3sin x ，x ∈R }，求M *N .B 组 专项能力提升题组一、选择题1．设集合A ＝{1,2,3,5,7}，B ＝{x ∈Z |1<x ≤6}，全集U ＝A ∪B ，则A ∩(∁U B )等于 ( )A ．{1,4,6,7}B ．{2,3,7}C ．{1,7}D ．{1} 2．设集合A ＝{1,2,3,4,5,6}，B ＝{4,5,6,7,8}，则满足S ⊆A 且S ∩B ≠∅的集合S 的个数是( ) A ．57B ．56C ．49D ．8 3．已知U ＝{y |y ＝log 2x ，x >1}，P ＝{y |y ＝1x，x >2}，则∁U P 等于( )A.⎣⎡⎭⎫12，＋∞B.⎝⎛⎭⎫0，12C ．(0，＋∞)D ．(－∞，0]∪⎣⎡⎭⎫12，＋∞ 4．已知集合A ＝{x |log 2x ＋1>0}，B ＝{y |y ＝3－2x －x 2}，则(∁R A )∩B 等于( )A.⎣⎡⎦⎤0，12B.⎝⎛⎦⎤0，12 C ．(－3,2] D.⎣⎡⎦⎤－3，12 二、填空题5．已知集合A ＝(－∞，0]，B ＝{1,3，a }，若A ∩B ≠∅，则实数a 的取值范围是________． 6．设U ＝{0,1,2,3}，A ＝{x ∈U |x 2＋mx ＝0}，若∁U A ＝{1,2}，则实数m ＝________. 7．设A ＝{x ||x |≤3}，B ＝{y |y ＝－x 2＋t }，若A ∩B ＝∅，则实数t 的取值范围是__________． 三、解答题8．已知集合A ＝{x |x －5x ＋1≤0}，B ＝{x |x 2－2x －m <0}，(1)当m ＝3时，求A ∩(∁R B )；(2)若A ∩B ＝{x |－1<x <4}，求实数m 的值． 答案 要点梳理1．(1)确定性 互异性 无序性 2)属于 不属于 ∈ ∉ (3)列举法 描述法 图示法 区间法 (5)有限集 无限集 空集2．(1)A B B A ⊆ ⊆ ⊆ 2n 2n －1 2n －2 3．(1){x |x ∈A ，且x ∈B } {x |x ∈U ，且x ∉A } 基础自测1．{2,4} 2.{x |0<x <1}3.⎩⎨⎧⎭⎬⎫0，1，－12 4.D 5.B 题型分类·深度剖析例1 解 (1)当a ＋2＝1，即a ＝－1时， (a ＋1)2＝0，a 2＋3a ＋3＝1与a ＋2相同， ∴不符合题意．当(a ＋1)2＝1，即a ＝0或a ＝－2时， ①a ＝0符合要求．②a ＝－2时，a 2＋3a ＋3＝1与(a ＋1)2相同，不符合题意． 当a 2＋3a ＋3＝1，即a ＝－2或a ＝－1.①当a ＝－2时，a 2＋3a ＋3＝(a ＋1)2＝1，不符合题意． ②当a ＝－1时，a 2＋3a ＋3＝a ＋2＝1，不符合题意． 综上所述，a ＝0. ∴2 013a ＝1.(2)因为当x ＝0时，x ＝x 2－x ＝x 3－3x ＝0. 所以它不一定能表示一个有三个元素的集合． 要使它表示一个有三个元素的集合，则应有⎩⎪⎨⎪⎧x ≠x 2－x ，x 2－x ≠x 3－3x ，x ≠x 3－3x .∴x ≠0且x ≠2且x ≠－1且x ≠－2时，{x ，x 2－x ，x 3－3x }能表示一个有三个元素的集合．变式训练1 0或98例2 解 A 中不等式的解集应分三种情况讨论： ①若a ＝0，则A ＝R ；②若a <0，则A ＝⎩⎨⎧⎭⎬⎫x |4a ≤x <－1a ；③若a >0，则A ＝⎩⎨⎧⎭⎬⎫x |－1a <x ≤4a .(1)当a ＝0时，若A ⊆B ，此种情况不存在． 当a <0时，若A ⊆B ，如图，则⎩⎨⎧4a >－12－1a ≤2，∴⎩⎪⎨⎪⎧a >0或a <－8a >0或a ≤－12，又a <0，∴a <－8.当a >0时，若A ⊆B ，如图，则⎩⎨⎧－1a ≥－124a ≤2，∴⎩⎪⎨⎪⎧a ≥2或a <0a ≥2或a <0.又∵a >0，∴a ≥2.综上知，当A ⊆B 时，a <－8或a ≥2. (2)当a ＝0时，显然B ⊆A ； 当a <0时，若B ⊆A ，如图，则⎩⎨⎧4a ≤－12－1a >2，∴⎩⎪⎨⎪⎧－8≤a <0－12<a <0.又∵a <0，∴－12<a <0.当a >0时，若B ⊆A ，如图，则⎩⎨⎧－1a ≤－124a ≥2，∴⎩⎪⎨⎪⎧0<a ≤20<a ≤2.又∵a >0，∴0<a ≤2.综上知，当B ⊆A 时，－12<a ≤2.(3)当且仅当A 、B 两个集合互相包含时，A ＝B . 由(1)、(2)知，a ＝2. 变式训练2 4 例3 1或2变式训练3 解 (1)∵A ＝{x |12≤x ≤3}，当a ＝－4时，B ＝{x |－2<x <2}，∴A ∩B ＝{x |12≤x <2}，A ∪B ＝{x |－2<x ≤3}．(2)∁R A ＝{x |x <12或x >3}，当(∁R A )∩B ＝B 时，B ⊆∁R A ， 即A ∩B ＝∅.①当B ＝∅，即a ≥0时，满足B ⊆∁R A ；②当B ≠∅，即a <0时，B ＝{x |－－a <x <－a }，要使B ⊆∁R A ，需－a ≤12，解得－14≤a <0.综上可得，实数a 的取值范围是a ≥－14.例4 A变式训练4 6 {0,1,2,3} 课时规范训练 A 组1．C 2.C 3.A4．－1或2 5.{(0,1)，(－1,2)} 6．187．解 由已知得A ＝{x |－1≤x ≤3}，B ＝{x |m －2≤x ≤m ＋2}．(1)∵A ∩B ＝[0,3]，∴⎩⎪⎨⎪⎧m －2＝0，m ＋2≥3.∴m ＝2.(2)∁R B ＝{x |x <m －2或x >m ＋2}， ∵A ⊆∁R B ，∴m －2>3或m ＋2<－1， 即m >5或m <－3.8．解 ∵M ＝{y |y ＝x 2，x ∈R }＝{y |y ≥0}，N ＝{y |y ＝3sin x ，x ∈R }＝{y |－3≤y ≤3}， ∴M －N ＝{y |y >3}， N －M ＝{y |－3≤y <0}， ∴M *N ＝(M －N )∪(N －M ) ＝{y |y >3}∪{y |－3≤y <0} ＝{y |y >3或－3≤y <0}． B 组1．C 2．B 3．A 4．A 5．a ≤0 6．－37．(－∞，－3)8．解 由x －5x ＋1≤0，所以－1<x ≤5，所以A ＝{x |－1<x ≤5}． (1)当m ＝3时，B ＝{x |－1<x <3}， 则∁R B ＝{x |x ≤－1或x ≥3}， 所以A ∩(∁R B )＝{x |3≤x ≤5}． (2)因为A ＝{x |－1<x ≤5}， A ∩B ＝{x |－1<x <4}，所以有42－2×4－m ＝0，解得m ＝8. 此时B ＝{x |－2<x <4}，符合题意， 故实数m 的值为8.。

§1.1集合及其运算1．集合与元素(1)集合中元素的三个特征：确定性、互异性、无序性．(2)元素与集合的关系是属于或不属于，用符号∈或∉表示．(3)集合的表示法：列举法、描述法、图示法．(4)常见数集的记法2.集合间的基本关系A B (或B A )3.集合的基本运算知识拓展1．若有限集合A 中有n 个元素，则集合A 的子集个数为2n ，真子集的个数为2n －1. 2．A ⊆B ⇔A ∩B ＝A ⇔A ∪B ＝B .3．A ∩(∁U A )＝∅；A ∪(∁U A )＝U ；∁U (∁U A )＝A .题组一 思考辨析1．判断下列结论是否正确(请在括号中打“√”或“×”) (1)任何一个集合都至少有两个子集．( × )(2){x |y ＝x 2＋1}＝{y |y ＝x 2＋1}＝{(x ，y )|y ＝x 2＋1}．( × )(3)若{x 2,1}＝{0,1}，则x ＝0,1.( × ) (4){x |x ≤1}＝{t |t ≤1}．( √ )(5)对于任意两个集合A ，B ，关系(A ∩B )⊆(A ∪B )恒成立．( √ ) (6)若A ∩B ＝A ∩C ，则B ＝C .( × ) 题组二 教材改编2．[P11例9]已知U ＝{α|0°＜α＜180°}，A ＝{x |x 是锐角}，B ＝{x |x 是钝角}，则∁U (A ∪B )＝________.答案 {x |x 是直角}3．[P44A 组T5]已知集合A ＝{(x ，y )|x 2＋y 2＝1}，B ＝{(x ，y )|y ＝x }，则A ∩B 中元素的个数为________． 答案 2解析 集合A 表示以(0,0)为圆心，1为半径的单位圆，集合B 表示直线y ＝x ，圆x 2＋y 2＝1与直线y ＝x 相交于两点⎝⎛⎭⎫22，22，⎝⎛⎭⎫－22，－22，则A ∩B 中有两个元素． 题组三 易错自纠4．已知集合A ＝{1,3，m }，B ＝{1，m }，A ∪B ＝A ，则m 等于( ) A ．0或 3 B ．0或3 C ．1或 3 D ．1或3或0答案 B解析 A ＝{1,3，m }，B ＝{1，m }，A ∪B ＝A ，故B ⊆A ，所以m ＝3或m ＝m ，即m ＝3或m ＝0或m ＝1，其中m ＝1不符合题意，所以m ＝0或m ＝3，故选B.5．已知集合A ＝{x |x 2－2x －3≤0}，B ＝{x |x <a }，若A ⊆B ，则实数a 的取值范围是____________． 答案 (3，＋∞)解析 A ＝{x |x 2－2x －3≤0}＝{x |－1≤x ≤3}， ∵A ⊆B ，B ＝{x |x <a }，∴a >3.6．若集合A ＝{x ∈R |ax 2－3x ＋2＝0}中只有一个元素，则a ＝________. 答案 0或98解析 若a ＝0，则A ＝⎩⎨⎧⎭⎬⎫23，符合题意；若a ≠0，则由题意得Δ＝9－8a ＝0，解得a ＝98.综上，a 的值为0或98.题型一集合的含义1．设集合A＝{－1,1,3}，B＝{a＋2，a2＋4}，A∩B＝{3}，则实数a＝________.答案 1解析∵3∈B，又a2＋4≥4，∴a＋2＝3，∴a＝1.经检验，a＝1符合题意．2．若A＝{2,3,4}，B＝{x|x＝n·m，m，n∈A，m≠n}，则集合B中的元素个数是()A．2 B．3 C．4 D．5答案 B解析B＝{x|x＝n·m，m，n∈A，m≠n}＝{6,8,12}．思维升华(1)用描述法表示集合，首先要搞清楚集合中代表元素的含义，再看元素的限制条件，明白集合的类型，是数集、点集还是其他类型的集合．(2)集合中元素的互异性常常容易忽略，求解问题时要特别注意．分类讨论的思想方法常用于解决集合问题．题型二集合的基本关系典例(1)设A，B是全集I＝{1,2,3,4}的子集，A＝{1,2}，则满足A⊆B的集合B的个数是() A．5 B．4 C．3 D．2答案 B解析∵{1,2}⊆B，I＝{1,2,3,4}，∴满足条件的集合B有{1,2}，{1,2,3}，{1,2,4}，{1,2,3,4}，共4个．(2)已知集合A＝{x|x2－2 019x＋2 018<0}，B＝{x|x<a}，若A⊆B，则实数a的取值范围是________________________．答案[2 018，＋∞)解析由x2－2 019x＋2 018<0，解得1<x<2 018，故A＝{x|1<x<2 018}．又B＝{x|x<a}，A⊆B，如图所示，可得a≥2 018.引申探究本例(2)中，若将集合B改为{x|x≥a}，其他条件不变，则实数a的取值范围是____________．答案(－∞，1]解析 A ＝{x |1<x <2 018}，B ＝{x |x ≥a }，A ⊆B ，如图所示，可得a ≤1.思维升华 (1)空集是任何集合的子集，在涉及集合关系时，必须优先考虑空集的情况，否则会造成漏解．(2)已知两个集合间的关系求参数时，关键是将条件转化为元素或区间端点间的关系，进而转化为参数所满足的关系，常用数轴、Venn 图等来直观解决这类问题．跟踪训练 (1)已知集合A ＝{x ∈R |x 2＋x －6＝0}，B ＝{x ∈R |ax －1＝0}，若B ⊆A ，则实数a 的值为( ) A.13或－12 B ．－13或12C.13或－12或0 D ．－13或12或0答案 D解析 由题意知，A ＝{2，－3}． 当a ＝0时，B ＝∅，满足B ⊆A ； 当a ≠0时，ax －1＝0的解为x ＝1a ，由B ⊆A ，可得1a ＝－3或1a ＝2，∴a ＝－13或a ＝12.综上可知，a 的值为－13或12或0.(2)已知集合A ＝{x |－2≤x ≤7}，B ＝{x |m ＋1<x <2m －1}，若B ⊆A ，则实数m 的取值范围是____________． 答案 (－∞，4]解析 当B ＝∅时，有m ＋1≥2m －1，则m ≤2；当B ≠∅时，若B ⊆A ，如图， 则⎩⎪⎨⎪⎧m ＋1≥－2，2m －1≤7，m ＋1<2m －1， 解得2<m ≤4.综上，m 的取值范围是(－∞，4]．题型三集合的基本运算命题点1集合的运算典例(1)(2017·全国Ⅰ)已知集合A＝{x|x<1}，B＝{x|3x<1}，则()A．A∩B＝{x|x<0} B．A∪B＝RC．A∪B＝{x|x>1} D．A∩B＝∅答案 A解析∵B＝{x|3x<1}，∴B＝{x|x<0}．又A＝{x|x<1}，∴A∩B＝{x|x<0}，A∪B＝{x|x<1}．(2)(2018届珠海二中月考)已知集合A＝{x|x2－2x>0}，B＝{x|－5<x<5}，则()A．A∩B＝∅B．A⊆BC．B⊆A D．A∪B＝R答案 D解析∵A＝{x|x>2或x<0}，∴A∪B＝R.命题点2利用集合的运算求参数典例(1)设集合A＝{x|－1≤x<2}，B＝{x|x<a}，若A∩B≠∅，则a的取值范围是() A．－1<a≤2 B．a>2C．a≥－1 D．a>－1答案 D解析因为A∩B≠∅，所以集合A，B有公共元素，作出数轴，如图所示，易知a>－1.(2)集合A＝{0,2，a}，B＝{1，a2}，若A∪B＝{0,1,2,4,16}，则a的值为()A．0 B．1 C．2 D．4答案 D解析由题意可得{a，a2}＝{4,16}，∴a＝4.(3)设集合A＝{0，－4}，B＝{x|x2＋2(a＋1)x＋a2－1＝0，x∈R}．若A∩B＝B，则实数a的取值范围是______．答案(－∞，－1]∪{1}解析因为A＝{0，－4}，所以B⊆A分以下三种情况：①当B＝A时，B＝{0，－4}，由此可知，0和－4是方程x2＋2(a＋1)x＋a2－1＝0的两个根，由根与系数的关系，得⎩⎪⎨⎪⎧Δ＝4(a ＋1)2－4(a 2－1)>0，－2(a ＋1)＝－4，a 2－1＝0，解得a ＝1；②当B ≠∅且B A 时，B ＝{0}或B ＝{－4}， 并且Δ＝4(a ＋1)2－4(a 2－1)＝0， 解得a ＝－1，此时B ＝{0}满足题意； ③当B ＝∅时，Δ＝4(a ＋1)2－4(a 2－1)<0， 解得a <－1.综上所述，所求实数a 的取值范围是(－∞，－1]∪{1}．思维升华 (1)一般来讲，集合中的元素若是离散的，则用Venn 图表示；集合中的元素若是连续的，则用数轴表示，此时要注意端点的情况．(2)运算过程中要注意集合间的特殊关系的使用，灵活使用这些关系，会使运算简化． 跟踪训练 (1)(2017·天津)设集合A ＝{1,2,6}，B ＝{2,4}，C ＝{x ∈R |－1≤x ≤5}，则(A ∪B )∩C 等于( ) A ．{2} B ．{1,2,4}C ．{1,2,4,6}D ．{x ∈R |－1≤x ≤5}答案 B解析 A ∪B ＝{1,2,4,6}．又C ＝{x ∈R |－1≤x ≤5}，则(A ∪B )∩C ＝{1,2,4}．(2)已知集合A ＝{x |x 2－x －12≤0}，B ＝{x |2m －1<x <m ＋1}，且A ∩B ＝B ，则实数m 的取值范围为( ) A ．[－1,2) B ．[－1,3] C ．[2，＋∞) D ．[－1，＋∞)答案 D解析 由x 2－x －12≤0，得(x ＋3)(x －4)≤0， 即－3≤x ≤4，所以A ＝{x |－3≤x ≤4}． 又A ∩B ＝B ，所以B ⊆A .①当B ＝∅时，有m ＋1≤2m －1，解得m ≥2； ②当B ≠∅时，有⎩⎪⎨⎪⎧－3≤2m －1，m ＋1≤4，2m －1<m ＋1，解得－1≤m <2.综上，m 的取值范围为[－1，＋∞)．题型四集合的新定义问题典例若集合E＝{(p，q，r，s)|0≤p<s≤4,0≤q<s≤4,0≤r<s≤4且p，q，r，s∈N}，F＝{(t，u，v，w)|0≤t<u≤4,0≤v<w≤4且t，u，v，w∈N}，用card(X)表示集合X中的元素个数，则card(E)＋card(F)等于()A．200 B．150C．100 D．50答案 A解析在集合E中，当s＝1时，p＝q＝r＝0，此时只有1个元素；当s＝2时，p，q，r∈{0,1}，此时有2×2×2＝8(个)元素；当s＝3时，p，q，r∈{0,1,2}，此时有3×3×3＝27(个)元素；当s＝4时，p，q，r∈{0,1,2,3}，此时有4×4×4＝64(个)元素，故card(E)＝1＋8＋27＋64＝100.在集合F中，(t，u)的取值可能是(0,1)，(0,2)，(0,3)，(0,4)，(1,2)，(1,3)，(1,4)，(2,3)，(2,4)，(3,4)，共10种可能．同理，(v，w)也有10种可能，故card(F)＝10×10＝100，∴card(E)＋card(F)＝200.思维升华解决以集合为背景的新定义问题，要抓住两点：(1)紧扣新定义．首先分析新定义的特点，把新定义所叙述的问题的本质弄清楚，应用到具体的解题过程之中．(2)用好集合的性质．解题时要善于从试题中发现可以使用集合性质的一些因素．跟踪训练定义一种新的集合运算△：A△B＝{x|x∈A，且x∉B}．若集合A＝{x|x2－4x＋3<0}，B＝{x|2≤x≤4}，则按运算△，B△A等于()A．{x|3<x≤4} B．{x|3≤x≤4}C．{x|3<x<4} D．{x|2≤x≤4}答案 B解析A＝{x|1<x<3}，B＝{x|2≤x≤4}，由题意知，B△A＝{x|x∈B，且x∉A}＝{x|3≤x≤4}．1．已知集合A＝{1,2,3}，B＝{2,3}，则()A．A＝B B．A∩B＝∅C．A B D．B A答案 D2．(2017·浙江)已知集合P＝{x|－1＜x＜1}，Q＝{x|0＜x＜2}，则P∪Q等于()A．(－1,2) B．(0,1)C．(－1,0) D．(1,2)答案 A解析∵P＝{x|－1＜x＜1}，Q＝{x|0＜x＜2}，∴P∪Q＝{x|－1＜x＜2}．3．(2016·四川)设集合A＝{x|－2≤x≤2}，Z为整数集，则集合A∩Z中元素的个数是() A．3 B．4C．5 D．6答案 C解析由题意可知，A∩Z＝{－2，－1,0,1,2}，则A∩Z中的元素的个数为5.故选C. 4．(2017·吉林大学附中模拟)若集合A＝{x∈N|5＋4x－x2>0}，B＝{x|x<3}，则A∩B等于() A．∅B．{1,2}C．[0,3) D．{0,1,2}答案 D解析由A中不等式变形，得(x－5)(x＋1)<0，x∈N，解得－1<x<5，x∈N，即A＝{0,1,2,3,4}，∵B＝{x|x<3}，∴A∩B＝{0,1,2}．5．(2018·潍坊调研)已知全集U＝R，集合A＝{1,2,3,4,5}，B＝{x∈R|x≥2}，则图中阴影部分所表示的集合为()A．{0,1} B．{1}C．{1,2} D．{0,1,2}答案 B解析因为A∩B＝{2,3,4,5}，而图中阴影部分为集合A去掉A∩B部分，所以阴影部分所表示的集合为{1}．6．已知集合M＝{1,2,3,4}，则集合P＝{x|x∈M，且2x∉M}的子集的个数为()A．8 B．4C．3 D．2答案 B解析由题意得P＝{3,4}，∴集合P有4个子集．7．(2017·全国Ⅱ)设集合A＝{1,2,4}，B＝{x|x2－4x＋m＝0}．若A∩B＝{1}，则B等于() A．{1，－3} B．{1,0}C．{1,3} D．{1,5}答案 C解析∵A∩B＝{1}，∴1∈B.∴1－4＋m＝0，即m＝3.∴B ＝{x |x 2－4x ＋3＝0}＝{1,3}．故选C.8．已知集合A ＝{x |－1<x <0}，B ＝{x |x ≤a }，若A ⊆B ，则a 的取值范围为( ) A ．(－∞，0] B ．[0，＋∞) C ．(－∞，0) D ．(0，＋∞)答案 B解析 用数轴表示集合A ，B (如图)，由A ⊆B ，得a ≥0.9．已知集合P ＝{x |x 2－2x ≥0}，Q ＝{x |1＜x ≤2}，则(∁R P )∩Q ＝________.答案 (1,2)解析 ∵P ＝{x |x ≥2或x ≤0}，∁R P ＝{x |0＜x ＜2}， ∴(∁R P )∩Q ＝{x |1＜x ＜2}．10．若{3,4，m 2－3m －1}∩{2m ，－3}＝{－3}，则m ＝______. 答案 1解析 由集合中元素的互异性，可得⎩⎪⎨⎪⎧m 2－3m －1＝－3，2m ≠－3，2m ≠3，2m ≠4，所以m ＝1.11．(2018·衡水模拟)若集合A ＝{y |y ＝lg x }，B ＝{x |y ＝x }，则集合A ∩B ＝________.答案 [0，＋∞)解析 集合A ＝{y |y ＝lg x }＝{y |y ∈R }＝R ， B ＝{x |y ＝x }＝{x |x ≥0}，则集合A ∩B ＝{x |x ≥0}＝[0，＋∞)．12．已知集合A ＝{x |y ＝lg(x －x 2)}，B ＝{x |x 2－cx <0，c >0}，若A ⊆B ，则实数c 的取值范围是________． 答案 [1，＋∞)解析 由题意知，A ＝{x |y ＝lg(x －x 2)}＝{x |x －x 2>0}＝(0,1)，B ＝{x |x 2－cx <0，c >0}＝(0，c )．由A ⊆B ，画出数轴，如图所示，得c ≥1.13．(2017·安徽黄山二模)已知集合A ＝{－2，－1,0,1,2}，∁R B ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x －1x ＋2≥0，则A ∩B 等于( )A ．{－1,0,1}B ．{－1,0}C ．{－2，－1,0}D ．{0,1,2} 答案 C解析 ∵集合A ＝{－2，－1,0,1,2}，∁R B ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x －1x ＋2≥0＝{x |x <－2或x ≥1}， ∴B ＝{x |－2≤x <1}，则A ∩B ＝{－2，－1,0}．14．已知集合A ＝{x ∈R ||x ＋2|<3}，集合B ＝{x ∈R |(x －m )(x －2)<0}，且A ∩B ＝(－1，n )，则m ＝______，n ＝________.答案 －1 1解析 A ＝{x ∈R ||x ＋2|<3}＝{x ∈R |－5<x <1}，由A ∩B ＝(－1，n )，可知m <1，则B ＝{x |m <x <2}，画出数轴，可得m ＝－1，n ＝1.15．设A 是整数集的一个非空子集，对于k ∈A ，如果k －1∉A ，且k ＋1∉A ，那么称k 是A 的一个“孤立元”．给定S ＝{1,2,3,4,5,6,7,8}，由S 的3个元素构成的所有集合中，不含“孤立元”的集合共有________个．答案 6解析 依题意可知，由S 的3个元素构成的所有集合中，不含“孤立元”时，这三个元素一定是连续的三个自然数．故这样的集合共有6个．16．已知集合A ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪ 6x ＋1≥1，x ∈R ，B ＝{x |x 2－2x －m <0}，若A ∩B ＝{x |－1<x <4}，则实数m 的值为______．答案 8解析 由6x ＋1≥1，得x －5x ＋1≤0， ∴－1<x ≤5，∴A ＝{x |－1<x ≤5}．又∵B ＝{x |x 2－2x －m <0}，A∩B＝{x|－1<x<4}，∴4是方程x2－2x－m＝0的根，即42－2×4－m＝0，解得m＝8. 此时B＝{x|－2<x<4}，符合题意，故实数m的值为8.。