广东省东莞市2015届高三数学理小综合专题练习：立体几何

专题十 立体几何1.【2015高考安徽，理5】已知m ，n 是两条不同直线，α，β是两个不同平面，则下列命题正确的是（ ）（A ）若α，β垂直于同一平面，则α与β平行（B ）若m ，n 平行于同一平面，则m 与n 平行（C ）若α，β不平行，则在α内不存在与β平行的直线（D ）若m ，n 不平行，则m 与n 不可能垂直于同一平面【答案】D【解析】由A ，若α，β垂直于同一平面，则α，β可以相交、平行，故A 不正确；由B ，若m ，n 平行于同一平面，则m ，n 可以平行、重合、相交、异面，故B 不正确；由C ，若α，β不平行，但α平面内会存在平行于β的直线，如α平面中平行于α，β交线的直线；由D 项，其逆否命题为“若m 与n 垂直于同一平面，则m ，n 平行”是真命题，故D 项正确.所以选D.【考点定位】1.直线、平面的垂直、平行判定定理以及性质定理的应用.【名师点睛】空间直线、平面平行或垂直等位置关系命题的真假判断，常采用画图（尤其是画长方体）、现实实物判断法（如墙角、桌面等）、排除筛选法等；另外，若原命题不太容易判断真假，可以考虑它的逆否命题，判断它的逆否命题真假，原命题与逆否命题等价.2.【2015高考北京，理4】设α，β是两个不同的平面，m 是直线且m α⊂．“m β∥”是“αβ∥”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件 【答案】B【解析】因为α，β是两个不同的平面，m 是直线且m α⊂．若“m β∥”，则平面、αβ可能相交也可能平行，不能推出//αβ，反过来若//αβ，m α⊂，则有m β∥，则“m β∥”是“αβ∥”的必要而不充分条件.考点定位：本题考点为空间直线与平面的位置关系，重点考察线面、面面平行问题和充要条件的有关知识.【名师点睛】本题考查空间直线与平面的位置关系及充要条件，本题属于基础题，本题以空间线、面位置关系为载体，考查充要条件．考查学生对空间线、面的位置关系及空间面、面的位置关系的理解及空间想象能力，重点是线面平行和面面平行的有关判定和性质.3.【2015高考新课标1，理6】《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺。

三、解答题1. 【2015高考天津，理17】（本小题满分13分）如图，在四棱柱1111ABCD A B C D -中，侧棱1A A ABCD ⊥底面,AB AC ⊥,1AB =,12,5AC AA ADCD ====,且点M 和N 分别为11C D B D 和的中点.(I)求证：//MN 平面ABCD ； (II)求二面角11D AC B --的正弦值；(III)设E 为棱11A B 上的点，若直线NE 和平面ABCD 所成角的正弦值为13，求线段1A E 的长 【答案】(I)见解析； (II)31010； (III) 72-. 【解析】如图，以A 为原点建立空间直角坐标系，依题意可得(0,0,0),(0,1,0),(2,0,0),(1,2,0)A B C D -，NMC 1B 11DABD 1NM C 1B 1A 1DABCD 1(III)依题意，可设111A E A B λ=u u u r u u u u r ，其中[0,1]λ∈，则(0,,2)E λ，从而(1,2,1)NE λ=-+u u u r ，又(0,0,1)n =r为平面ABCD 的一个法向量，由已知得2221cos ,3(1)(2)1NE n NE n NE n λ⋅===⋅-+++u u u r ru u u r r u u u r r ，整理得2430λλ+-=， 又因为[0,1]λ∈，解得72λ=-，所以线段1A E 的长为72 .【考点定位】直线和平面平行和垂直的判定与性质，二面角、直线与平面所成的角，空间向量的应用.4. 【2013天津，理17】如图，四棱柱ABCD －A 1B 1C 1D 1中，侧棱A 1A ⊥底面ABCD ，AB ∥DC ，AB ⊥AD ，AD ＝CD ＝1，AA 1＝AB ＝2，E 为棱AA 1的中点．(1)证明B 1C 1⊥CE ；(2)求二面角B 1－CE －C 1的正弦值；(3)设点M 在线段C 1E 上，且直线AM 与平面ADD 1A 1所成角的正弦值为26，求线段AM 的长． 【答案】（Ⅰ）详见解析；（Ⅱ）217；（Ⅲ）2易得11B C u u u u r ＝(1,0，－1)，CE u u u r ＝(－1,1，－1)，于是11B C u u u u r ·CE u u u r＝0，所以B1C1⊥CE.(2)1B C u u u r＝(1，－2，－1)．设平面B1CE 的法向量m ＝(x ，y ，z),则10,0,B C CE ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r m m 即20,0.x y z x y z --=⎧⎨-+-=⎩(3)AE u u u r＝(0,1,0)，1EC u u u u r ＝(1,1,1)．设EM u u u u r ＝λ1EC u u u u r ＝(λ，λ，λ)，0≤λ≤1，有AM u u u u r ＝AE u u u r ＋EM u u u u r＝(λ，λ＋1，λ)．可取AB u u u r＝(0,0,2)为平面ADD1A1的一个法向量．设θ为直线AM 与平面ADD1A1所成的角，则sin θ＝|cos 〈AM u u u u r ，AB u u u r〉|＝AM AB AM AB⋅⋅u u u u r u u u r u u u ur u u u r 2222(1)2321λλλλλ=+++⨯++.22321λλ=++，解得13λ=,所以AM 2. (方法二)(1)证明：因为侧棱CC1⊥底面A1B1C1D1，B1C1⊂平面A1B1C1D1， 所以CC1⊥B1C1.经计算可得B1E ＝5，B1C1＝2，EC1＝3， 从而B1E2＝22111B C EC +， 所以在△B1EC1中，B1C1⊥C1E ，又CC1，C1E ⊂平面CC1E ，CC1∩C1E ＝C1， 所以B1C1⊥平面CC1E ，又CE ⊂平面CC1E ，故B1C1⊥CE.(3)连接D1E ，过点M 作MH ⊥ED1于点H ，可得MH ⊥平面ADD1A1，连接AH ，AM ，则∠MAH 为直线AM 与平面 ADD1A1所成的角．设AM ＝x ，从而在Rt △AHM 中，有MH ＝26x ，AH ＝346x . 在Rt △C1D1E 中，C1D1＝1，ED1＝2，得EH ＝123MH x.5. 【2014天津，理17】如图，在四棱锥P ABCD -中，PA ^底面ABCD ，AD AB ^，//AB DC ，2AD DC AP ===，1AB =，点E 为棱PC 的中点．E PDC（Ⅰ）证明：BE DC ^；（Ⅱ）求直线BE 与平面PBD 所成角的正弦值；（Ⅲ）若F 为棱PC 上一点，满足BF AC ^，求二面角F AB P --的余弦值． 【答案】（Ⅰ）详见试题分析；（Ⅱ）直线BE 与平面PBD 3；310． 【解析】试题分析：（Ⅰ）可以建立空间直角坐标系，利用向量数量积来证明BE DC ^。

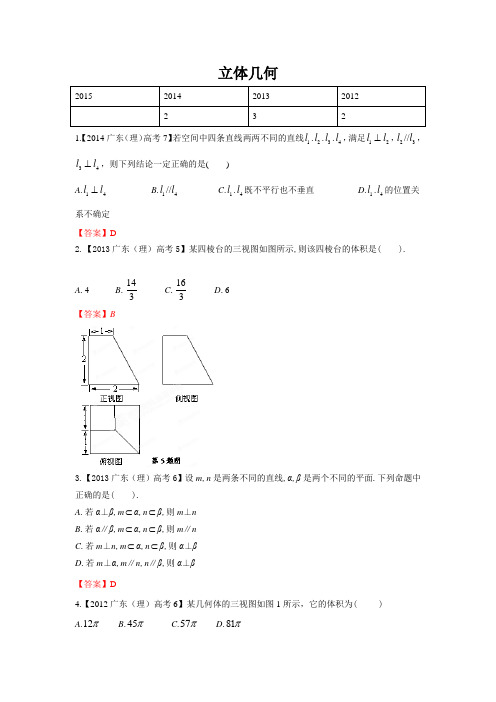
立体几何1.【2014广东（理）高考7】若空间中四条直线两两不同的直线1l .2l .3l .4l ，满足12l l ⊥，23//l l ，34l l ⊥，则下列结论一定正确的是( )A .14l l ⊥B .14//l lC .1l .4l 既不平行也不垂直D .1l .4l 的位置关系不确定 【答案】D2.【2013广东（理）高考5】某四棱台的三视图如图所示,则该四棱台的体积是( ).A .4B .143C .163D .6 【答案】B3.【2013广东（理）高考6】设m ,n 是两条不同的直线,α,β是两个不同的平面.下列命题中正确的是( ).A .若α⊥β,m ⊂α,n ⊂β,则m ⊥nB .若α∥β,m ⊂α,n ⊂β,则m ∥nC .若m ⊥n ,m ⊂α,n ⊂β,则α⊥βD .若m ⊥α,m ∥n ,n ∥β,则α⊥β 【答案】D4.【2012广东（理）高考6】某几何体的三视图如图1所示，它的体积为( ) A .12π B .45π C .π57 D .π81【答案】C5.【2014广东（理）高考18】 (本小题满分13分)如图4，四边形ABCD 为正方形，PD ⊥平面ABCD ，30DPC ∠=，AF PC ⊥于点F ，//FE CD ，交PD 于点E . (1)证明：CF ADF ⊥平面； (2)求二面角D AF E --的余弦值.【答案】(1)详见解析；(2)19. （１）PD ⊥平面ABCD ，PD AD ∴⊥，又CD AD ⊥，PD CD D =， AD ∴⊥平面PCD ，AD PC ∴⊥，又AF PC ⊥，PC ∴⊥平面ADF ，即CF ADF ⊥平面；（２）设1AB =，则Rt PDC ∆中，1CD =，又DPC ∠=2PC ∴=，PD =，由（１）知CF DF ⊥ DF ∴=AF ==12CF ∴==，又//FE CD ，14DE CF PD PC ∴==，DE ∴=，同理3344EF CD ==，如图所示，以D 为原点，建立空间直角坐标系，则(0,0,1)A ，E，3,0)4F，P ，(0,1,0)C ，设(,,)m x y z =是平面AEF 的法向量，则m AE m EF ⎧⊥⎨⊥⎩，又3(3(0,,0)4AE EF ⎧=⎪⎨=⎪⎩，所以304304m AE x z m EFy ⎧⋅=-=⎪⎨⋅==⎪⎩，令4x =，得z =，m =，由（１）知平面ADF 的一个法向量(,0)PC =， 设二面角D AF E --的平面角为θ，可知θ为锐角，||cos |cos ,|||||mPC m PC m PC ⋅=<>==⋅θ=，即所求．6.【2013广东（理）高考18】 (本小题满分14分)如图(1),在等腰直角三角形ABC 中,∠A ＝90°,BC ＝6,D ,E 分别是AC ,AB 上的点,CD ＝BEO为BC 的中点.将△ADE沿DE 折起,得到如图(2)所示的四棱锥A ′BCDE ,其中A ′O图(1)图(2)(1)证明：A ′O ⊥平面BCDE ；(2)求二面角A ′CDB的平面角的余弦值. 【答案】(1)详见解析 (2)5(Ⅰ) 在图1中,易得3,OC AC AD === 连结,OD OE ,在OCD ∆中,由余弦定理可得OD =由翻折不变性可知A D '=所以222A O OD A D ''+=,所以A O OD '⊥, 理可证A O OE '⊥, 又ODOE O =,所以A O '⊥平面BCDE .(Ⅱ) 传统法:过O 作OH CD ⊥交CD 的延长线于H ,连结A H ', 因为A O '⊥平面BCDE ,所以A H CD '⊥, 所以A HO '∠为二面角A CD B '--的平面角. 结合图1可知,H 为AC 中点,故2OH =,从而2A H '== 所以cos 5OH A HO A H '∠==',所以二面角A CD B '--.向量法:以O 点为原点,建立空间直角坐标系O xyz -则(A ',()0,3,0C -,()1,2,0D -所以(CA '=,(1,DA '=- 设(),,n x y z =为平面A CD '的法向量,则00n CA n DA ⎧'⋅=⎪⎨'⋅=⎪⎩,即3020y x y ⎧=⎪⎨-++=⎪⎩,解得y x z =-⎧⎪⎨=⎪⎩,令1x =,得(1,n =- 由(Ⅰ) 知,(OA '=为平面CDB 的一个法向量,所以cos ,3n OA n OA n OA '⋅'===',即二面角A CD B '--的平面角的余弦值为5.7.【2012广东（理）高考18】 (本小题满分13分)如图所示，在四棱锥P ABCD -中，底面ABCD 为矩形，PA ⊥平面ABCD ，点E 在线段PC 上，PC ⊥平面BDE . (1)证明：BD ⊥平面PAC ；(2)若1,2PA AD ==，求二面角B PC A --的正切值； 【答案】（1）证明：因为P A ⊥平面ABCD ，BD ⊂平面ABCD ，所以BD ⊥P A又因为PC⊥平面BDE，BD⊂平面BDE，BD⊥PC而P A∩PC=P，BD⊥平面P AC.（2）由（1）BD⊥平面P AC，得BD⊥AC，所以矩形ABCD为正方形设AC交BD于点O, 由PC⊥平面BDE,得PC垂直OE和BE所以∠BEO为二面角B－PC－A的平面角1,23PA AD AC BO OC PC==∴===∴==OE COOEPA PC===又所以在直角三角形BEO中，tan∠BEO33BOEO===，即二面角B-PC-A的正切值为3.8．（广东省湛江市湖光中学2014届高三上学期入学考试数学（理）试题）设三棱锥的三个侧面两两互相垂直,且侧棱长均为则其外接球的表面积为（）A．48πB．36πC．32πD．12π【答案】B9错误！未指定书签。

2015届高考理科数学立体几何一轮练习题-数学试题第1课时立体几何的结构及其三视图和直观图1．认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构．2．能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图，能识别上述三视图所表示的立体模型，会用斜二测画法画出它们的直观图．3．会用平行投影与中心投影两种方法画出简单空间图形的三视图与直观图，了解空间图形的不同表示形式．4．会画某些建筑物的三视图与直观图(在不影响图形特征的基础上，尺寸、线条等没有严格要求)．[对应学生用书P109]【梳理自测】一、空间几何体的结构特征1．(教材改编)下列说法正确的是()A．有两个面平行，其余各面都是四边形的几何体叫棱柱B．有两个面平行，其余各面都是平行四边形的几何体叫棱柱C．有一个面是多边形，其余各面都是三角形的几何体叫棱锥D．棱台各侧棱的延长线交于一点2．如图是一个正方体的展开图，将其折叠起来，变成正方体后的图形是()答案：1.D 2.B◆以上题目主要考查了以下内容：多面体棱柱棱柱的侧棱都平行且相等，上下底面是平行且全等的多边形．棱锥棱锥的底面是任意多边形，侧面是有一个公共顶点的三角形．棱台棱台可由平行于底面的平面截棱锥得到，其上下底面是平行且相似的多边形．旋转体圆柱圆柱可由矩形绕其任意一边所在直线旋转得到．圆锥圆锥可以由直角三角形绕其一条直角边所在直线旋转得到．圆台圆台可由直角梯形绕直角腰或等腰梯形绕上下底中点连线旋转得到，也可由平行于圆锥底面的平面截圆锥得到．球球可以由半圆或圆绕直径所在直线旋转得到.二、三视图1．有一个几何体的三视图如图所示，这个几何体应是一个()A．棱台B．棱锥C．棱柱D．都不对2．一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是()A．球B．三棱锥C．正方体D．圆柱答案：1.A 2.D◆以上题目主要考查了以下内容：名称几何体的三视图有：正视图、侧视图、俯视图画法1.画三视图时，重叠的线只画一条，挡住的线画成虚线. 2.三视图的正视图、侧视图、俯视图分别是从几何体的正前方、左方、正上方观察几何体得到的正投影图．规则1.画法规则：长对正、高平齐、宽相等. 2.摆放规则：侧视图在正视图的右侧，俯视图在正视图的下方.三、直观图及投影1．用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形，则原来的图形是()2．如图，过BC的平面截去长方体的一部分，所得的几何体________棱柱(填“是”或“不是”)．答案：1.A 2.是◆以上题目主要考查了以下内容：直观图空间几何体的直观图常用斜二测画法来画，其规则是：(1)原图形中x轴、y轴、z 轴两两垂直，直观图中，x′轴、y′轴的夹角为45°或135°，z′轴与x′轴和y′轴所在平面垂直. (2)原图形中平行于坐标轴的线段，直观图中仍平行于坐标轴，平行于x轴和z轴的线段长度在直观图中不变，平行于y轴的线段长度在直观图中等于原来的一半．投影1.平行投影：平行投影的投影线互相平行. 2.中心投影：中心投影的投影线相交于一点.【指点迷津】1．一个程序由三视图还原几何体按下面的程序进行定底面根据俯视图确定定棱及侧面根据正视图确定几何体的侧棱与侧面特征，调整实线、虚线对应棱的位置定形状确定几何体的形状2．三个“变”与“不变”斜二测画直观图时“三变”坐标轴的夹角改变，与y轴平行的线段的长度变为原来的一半，图形改变.“三不变”平行性不改变，与x、z轴平行的线段的长度不改变，相对位置不改变.[对应学生用书P110]考向一空间几何体的结构特征给出下列四个命题：①在圆柱的上、下底面的圆周上各取一点，则这两点的连线是圆柱的母线；②底面为正多边形，且有相邻两个侧面与底面垂直的棱柱是正棱柱；③直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥；④棱台的上、下底面可以不相似，但侧棱长一定相等．其中正确命题的个数是()A．0B．1C．2 D．3【审题视点】根据柱、锥、台几何体的结构特征判定．【典例精讲】①不一定，只有这两点的连线平行于轴时才是母线；②正确；③错误．当以斜边所在直线为旋转轴时，其余两边旋转形成的面所围成的几何体不是圆锥．如图所示，它是由两个同底圆锥组成的几何体；④错误，棱台的上、下底面是相似且对应边平行的多边形，各侧棱延长线交于一点，但是侧棱长不一定相等．【答案】B【类题通法】(1)紧扣结构特征是判断的关键，熟悉空间几何体的结构特征，依据条件构建几何模型，在条件不变的情况下，变换模型中的线面关系或增加线、面等基本元素，然后再依据题意判定．(2)通过反例对结构特征进行辨析，即要说明一个命题是错误的，只要举出一个反例即可．1．给出下列四个命题：①有两个侧面是矩形的棱柱是直棱柱；②侧面都是等腰三角形的棱锥是正棱锥；③侧面都是矩形的直四棱柱是长方体；④若有两个侧面垂直于底面，则该四棱柱为直四棱柱．其中不正确的命题的个数是________个．解析：认识棱柱一般要从侧棱与底面的垂直与否和底面多边形的形状两方面去分析，故①③都不准确，②中对等腰三角形的腰是否为侧棱未作说明，故也不正确，④平行六面体的两个相对侧面也可能与底面垂直且互相平行，故④也不正确．答案：4考向二空间几何体的三视图(2014&#8226;陕西省高三质检)如图是由若干个相同的小立方体组成的几何体的俯视图，其中小立方体中的数字表示相应位置的小立方体的个数，则该几何体的左视图为()【审题视点】从左侧看这个几何体中小立方体组成的几何体的高度．【典例精讲】由俯视图知左视图从左到右最高的小立方体个数分别为2，3，1，选C.【答案】C【类题通法】(1)由实物图画三视图或判断选择三视图，此时需要注意“长对正、高平齐、宽相等”的原则；(2)由三视图还原实物图，这一题型综合性较强，解题时首先对柱、锥、台、球的三视图要熟悉，再复杂的几何体也是由这些简单的几何体组合而成的；其次，要遵循以下三步：①看视图，明关系；②分部分，想整体；③综合起来，定整体．2．(2014&#8226;山西高考训练)某几何体的三视图均为直角三角形，如图所示，则围成该几何体的各面中，直角三角形的个数为()A．1B．2C．3 D．4解析：选D.依题意得，该几何体是一个底面为直角三角形、一条侧棱垂直于底面的三棱锥，其四个面均为直角三角形，选D.考向三空间几何体的直观图已知正三角形ABC的边长为a，那么◆ABC的平面直观图◆A′B′C′的面积为()A.34a2B.38a2C.68a2D.616a2【审题视点】画出正三角形◆ABC的平面直观图◆A′B′C′，求◆A′B′C′的高即可．【典例精讲】先画出正三角形ABC，然后再画出它的水平放置的直观图，如图所示，由斜二测画法规则知B′C′＝a，O′A′＝34a.过A′作A′M◆x′轴，垂足为M，则A′M＝O′A′&#8226;sin 45°＝34a×22＝68a.◆S◆A′B′C′＝12B′C′&#8226;A′M＝12a×68a＝616a2.【答案】D【类题通法】对于直观图，除了了解斜二测画法的规则外，还要了解原图形面积S与其直观图面积S′之间的关系S′＝24S，能进行相关问题的计算．3．如图所示，四边形A′B′C′D′是一平面图形的水平放置的斜二测画法的直观图，在斜二测直观图中，四边形A′B′C′D′是一直角梯形，A′B′◆C′D′，A′D′◆C′D′，且B′C′与y′轴平行，若A′B′＝6，D′C′＝4，A′D′＝2.求这个平面图形的实际面积．解析：根据斜二测直观图画法规则可知该平面图形是直角梯形，且AB＝6，CD＝4保持不变．由于C′B′＝2A′D′＝22.所以CB＝42.故平面图形的实际面积为12×(6＋4)×42＝202.[对应学生用书P111]忽视几何体的放置与特征致误在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为()【正解】由正视图和俯视图可以推测几何体为半圆锥和三棱锥的组合体(如图所示)，且顶点在底面的射影恰是底面半圆的圆心，可知侧视图为等腰三角形，且轮廓线为实线，故选D.【答案】D【易错点】(1)根据正视图和俯视图确定原几何体的形状时出现错误，误把半圆锥看成半圆柱，不能准确判断出几何体的形状而误选A.(2)对实线与虚线的画法规则不明确而误选C.【警示】 1.首先确定几何体，面对读者是怎么放置的．2．要分清三视图中的虚线是被哪部分挡住的．3．要明确三视图中三角形的高度是不是几何体的高度．1．(2013&#8226;高考四川卷)一个几何体的三视图如图所示，则该几何体的直观图可以是()解析：选D.先观察俯视图，再结合主视图和侧视图还原为空间几何体．由俯视图是圆环可排除A，B，C，进一步将已知三视图还原为几何体，可得选项D. 2．(2013&#8226;高考湖南卷)已知正方体的棱长为1，其俯视图是一个面积为1的正方形，侧视图是一个面积为2的矩形，则该正方体的正视图的面积等于()A.32B．1C.2＋12D.2解析：选D.根据正方体的俯视图及侧视图特征想象出其正视图后求面积．由于该正方体的俯视图是面积为1的正方形，侧视图是一个面积为2的矩形，因此该几何体的正视图是一个长为2，宽为1的矩形，其面积为2.3．(2012&#8226;高考陕西卷)将正方体(如图(1)所示)截去两个三棱锥，得到如图(2)所示的几何体，则该几何体的左视图为()解析：选B.还原正方体后，将D1，D，A三点分别向正方体右侧面作垂线．D1A的射影为C1B，且为实线，B1C被遮挡应为虚线．4．(2012&#8226;高考湖南卷)某几何体的正视图和侧视图均如图所示，则该几何体的俯视图不可能是()解析：选C.若为C选项，则主视图为：故不可能是C选项．。

2015届高三理科数学小综合专题练习——解析几何一、选择题1．已知两直线03:1=++my x l ，()0221:2=++-m my x m l ，若21//l l ，则m 的值为（ ）A ． 0B ． 1-或21C ．3D ．0或32．直线012=++y x 被圆25)1()2(22=-+-y x 所截得的弦长等于（ ） A.52 B.53 C.54 D.553．设P 是椭圆1162522=+y x 上的一点，21,F F 是焦点，若︒=∠3021PF F ，则21PF F ∆的面积为（ ）A.3316 B.)32(16- C. )32(16+ D.164．与曲线1492422=+y x 共焦点，且与曲线1643622=-y x 共渐近线的双曲线方程为（ ） A ．191622=-x y B ．191622=-y x C ．116922=-x y D ．116922=-y x5．设椭圆的两个焦点分别为1F 、2F ，过2F 作椭圆长轴的垂线交椭圆于点M ，若M F F 21∆为等腰直角三角形，则椭圆的离心率为（ ）A.22B.12-C.22-D.212-二、填空题6．直线210kx y k +++=必经过的点是 ．7．P 为圆122=+y x 上的动点，则点P 到直线01043=--y x 的距离的最小值为 ．8．已知抛物线)0(22>=p px y 的准线与直线03=-+y x 以及x 轴围成三角形面积为8，则p ＝__________________.9．若动圆M 与圆2)4(:221=++y x C 外切，且与圆2)4(:222=+-y x C 内切，则动圆圆心M 的轨迹方程________．10．已知双曲线)0,0(12222>>=-b a b y a x 和椭圆191622=+y x 有相同的焦点，且双曲线的离心率是椭圆离心率的两倍，则双曲线的方程为 _________ ．三、解答题11．已知椭圆)0,0(1:2222>>=+b a b y a x E 的离心率3 e =，并且经过定点1 (3,)2P （1）求椭圆 E 的方程；（2）问是否存在直线m x y +-=，使直线与椭圆交于B A , 两点，满足OA OB ⊥,若存在求 m 值，若不存在说明理由．12．椭圆2222:1(0)x y C a b a b +=>>过点3(1,)2A ，离心率为12，左、右焦点分别为12,F F ，过1F 的直线交椭圆于,A B 两点．（1）求椭圆C 的方程；（2）当2F AB∆的面积为27时，求直线的方程.13．无论m 为任何实数，直线m x y l +=:与双曲线)0(12:222>=-b b y x C 恒有公共点.（1）求双曲线C 的离心率e 的取值范围；（2）若直线l 过双曲线C 的右焦点F ，与双曲线交于Q P ,两点，并且满足→→=FQFP 51，求双曲线C 的方程.14．已知椭圆2222:1(0)x y C a b a b +=>>的两焦点与短轴的一个端点的连线构成等腰直角三角形，直线01=++y x 与以椭圆C 的右焦点为圆心，以b 2为半径的圆相切． （1）求椭圆的方程．（2）若过椭圆C 的右焦点F 作直线l 交椭圆C 于B A ,两点，交y 轴于M 点，且21,λλ==求证：21λλ+为定值15．已知抛物线y x C 4:2=的焦点为F ，过点F 作直线l 交抛物线C 于A 、B 两点；椭圆E 的中心在原点，焦点在x 轴上，点F 是它的一个顶点，且其离心率23=e ．（1）求椭圆E 的方程；（2）经过A 、B 两点分别作抛物线C 的切线1l 、2l ，切线1l 与2l 相交于点M ．证明：MF AB ⊥；（3） 椭圆E 上是否存在一点M '，经过点M '作抛物线C 的两条切线M A ''、M B ''（A '、B '为切点），使得直线A B ''过点F ？若存在，求出抛物线C 与切线M A ''、M B ''所围成图形的面积；若不存在，试说明理由．2015届高三理科数学小综合专题练习——解析几何参考答案 1．A【解析】由题，若0:1111=++C y B x A l ,0:2222=++C y B x A l ,当21//l l 时，有212121C C B B A A ≠=,故本题有m m m m 23211≠=-，即3≠m ，又因为当m=0，时，0:,3:21=-=x l x l ，因此，l1∥l2。

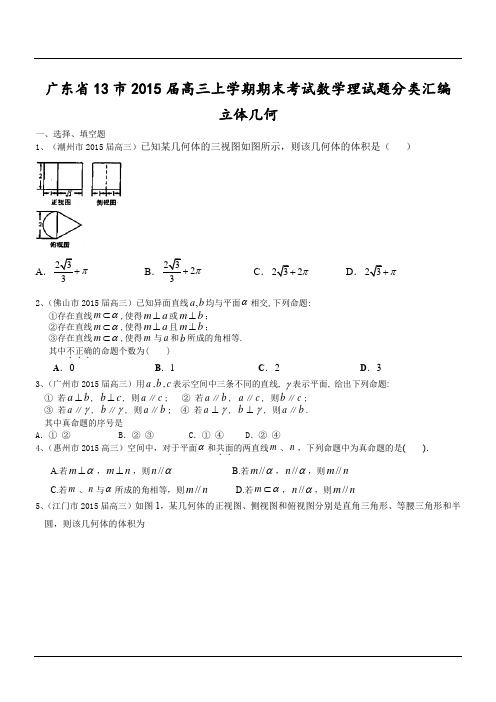
广东省13市2015届高三上学期期末考试数学理试题分类汇编立体几何一、选择、填空题1、（潮州市2015届高三）已知某几何体的三视图如图所示，则该几何体的体积是（ ）ABC ．D ． 2、（佛山市2015届高三）已知异面直线,a b 均与平面α相交,下列命题:①存在直线m α⊂,使得m a ⊥或m b ⊥； ②存在直线m α⊂,使得m a ⊥且m b ⊥；③存在直线m α⊂,使得m 与a 和b 所成的角相等. 其中不正确．．．的命题个数为( ) A ．0 B ．1 C ．2 D ．3 3、（广州市2015届高三）用a ,b ,c 表示空间中三条不同的直线, γ表示平面, 给出下列命题: ① 若a b ⊥, b c ⊥, 则a ∥c ; ② 若a ∥b , a ∥c , 则b ∥c ; ③ 若a ∥γ, b ∥γ, 则a ∥b ; ④ 若a ⊥γ, b ⊥γ, 则a ∥b . 其中真命题的序号是A ．① ②B ．② ③ C．① ④ D ．② ④4、（惠州市2015高三）空间中，对于平面和共面．．的两直线、，下列命题中为真命题的是( )． A.若，，则 B.若，，则 C.若、与所成的角相等，则 D.若，，则5、（江门市2015届高三）如图1，某几何体的正视图、侧视图和俯视图分别是直角三角形、等腰三角形和半圆，则该几何体的体积为π+2π+2ππαm n m α⊥m n ⊥//n α//m α//n α//m n m n α//m n m α⊂//n α//m nA ．4B ．8C ．π2D ．π46、（揭阳市2015届高三）一几何体的三视图如图3示, 则该几何体的体积为________7、（清远市2015届高三）某几何体的三视图如下图所示：其中正视图和侧视图都是上底为3，下底为9，高为4的等腰梯形，则该几何体的全面积为＿＿＿＿ 8、（汕头市2015届高三）给出下列命题，其中错误命题的个数为( ) （1）直线a 与平面不平行，则a 与平面内的所有直线都不平行； （2）直线a 与平面不垂直，则a 与平面内的所有直线都不垂直； （3）异面直线a 、b 不垂直，则过a 的任何平面与b 都不垂直； （4）若直线a 和b 共面，直线b 和c 共面，则a 和c 共面A ．1 B2 C3 D 4αααα9、（汕尾市2015届高三）已知直线l ⊥平面α，直线m ⊆平面β恒谦网，则下列四个结论：①若//αβ，则l m ⊥ ②若αβ⊥，则//l m③若//l m ，则αβ⊥④若l m ⊥，则//αβ。

立体几何1．一个物体的三视图的排列规则是俯视图放在正(主)视图下面，长度与正(主)视图一样，侧(左)视图放在正(主)视图右面，高度与正(主)视图一样，宽度与俯视图一样，即“长对正，高平齐，宽相等”．在画一个物体的三视图时，一定注意实线与虚线要分明．[问题1] 如图，若一个几何体的正(主)视图、侧(左)视图、俯视图均为面积等于2的等腰直角三角形，则该几何体的体积为________．2．在斜二测画法中，要确定关键点及关键线段．“平行于x 轴的线段平行性不变，长度不变；平行于y 轴的线段平行性不变，长度减半．”[问题2] 如图所示的等腰直角三角形表示一个水平放置的平面图形的直观图，则这个平面图形的面积是________．3．简单几何体的表面积和体积（1）S 直棱柱侧＝c ·h (c 为底面的周长，h 为高)． （2）S 正棱锥侧＝12ch ′(c 为底面周长，h ′为斜高)．（3）S 正棱台侧＝12(c ′＋c )h ′(c 与c ′分别为上、下底面周长，h ′为斜高)．（4）圆柱、圆锥、圆台的侧面积公式S 圆柱侧＝2πrl (r 为底面半径，l 为母线)， S 圆锥侧＝πrl (同上)， S 圆台侧＝π(r ′＋r )l (r ′、r 分别为上、下底的半径，l 为母线)． （5）体积公式V 柱＝S ·h (S 为底面面积，h 为高)， V 锥＝13S ·h (S 为底面面积，h 为高)，V 台＝13(S ＋SS ′＋S ′)h (S 、S ′为上、下底面面积，h 为高)．（6）球的表面积和体积S 球＝4πR 2，V 球＝43πR 3.[问题3] 如图所示，一个空间几何体的正(主)视图和俯视图都是边长为1的正方形，侧(左)视图是一个直径为1的圆，那么这个几何体的表面积为( )A ．4πB ．3πC ．2πD ．32π4．空间直线的位置关系：①相交直线——有且只有一个公共点．②平行直线——在同一平面内，没有公共点．③异面直线——不在同一平面内，也没有公共点．[问题4] 在空间四边形ABCD 中，E 、F 、G 、H 分别是四边上的中点，则直线EG 和FH 的位置关系是________． 5．空间直线与平面、平面与平面的位置关系 （1）直线与平面①位置关系：平行、直线在平面内、直线与平面相交． ②直线与平面平行的判定定理和性质定理：判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行．性质定理：一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行．③直线与平面垂直的判定定理和性质定理：判定定理：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直． 性质定理：垂直于同一个平面的两条直线平行． （2）平面与平面①位置关系：平行、相交(垂直是相交的一种特殊情况)． ②平面与平面平行的判定定理和性质定理：判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行． 性质定理：如果两个平行平面同时和第三个平面相交，那么它们的交线平行．③平面与平面垂直的判定定理和性质定理：判定定理：一个平面过另一个平面的垂线，则这两个平面垂直．性质定理：两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直．[问题5] 已知b ，c 是平面α内的两条直线，则“直线a ⊥α”是“直线a ⊥b ，直线a ⊥c ”的________条件．6．空间向量（1）用空间向量求角的方法步骤①异面直线所成的角若异面直线l 1和l 2的方向向量分别为v 1和v 2，它们所成的角为θ，则cos θ＝|cos 〈v 1，v 2〉|.②直线和平面所成的角利用空间向量求直线与平面所成的角，可以有两种方法：方法一 分别求出斜线和它在平面内的射影直线的方向向量，转化为求两条直线的方向向量的夹角(或其补角)．方法二 通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角，取其余角就是斜线和平面所成的角．③利用空间向量求二面角也有两种方法：方法一 分别在二面角的两个面内找到一个与棱垂直且从垂足出发的两个向量，则这两个向量的夹角的大小就是二面角的平面角的大小．方法二 通过平面的法向量来求，设二面角的两个面的法向量分别为n 1和n 2，则二面角的大小等于〈n 1，n 2〉(或π－〈n 1，n 2〉)．易错警示：①求线面角时，得到的是直线方向向量和平面法向量的夹角的余弦，容易误以为是线面角的余弦． ②求二面角时，两法向量的夹角有可能是二面角的补角，要注意从图中分析． （2）用空间向量求A 到平面α的距离：可表示为d ＝|n ·AB →||n |.[问题6] （1）已知正三棱柱ABC －A 1B 1C 1的侧棱长与底面边长相等，则AB 1与侧面ACC 1A 1所成角的正弦值等于________．（2）正方体ABCD －A 1B 1C 1D 1的棱长为1，O 是底面A 1B 1C 1D 1的中心，则点O 到平面ABC 1D 1的距离为________．易错点1 三视图认识不清致误例1 一个空间几何体的三视图如图所示，则该几何体的表面积为()A ．48B ．32＋817C ．48＋817D ．80找准失分点 不能准确把握三视图和几何体之间的数量关系，根据正视图可知，侧视图中等腰梯形的高为4，而错认为等腰梯形的腰为4.易错点2 对几何概念理解不透致误例2 给出下列四个命题：①有两个平面互相平行，其余各面都是平行四边形的多面体是棱柱； ②若两个过相对侧棱的截面都垂直于底面，则该四棱柱为直四棱柱； ③底面是平行四边形的四棱柱是平行六面体； ④底面是矩形的平行六面体是长方体．其中正确的命题是__________(写出所有正确命题的序号)．找准失分点 ①是错误的，因为棱柱的侧棱要都平行且相等；④是错误的，因为长方体的侧棱必须与底面垂直．易错点3 对线面关系定理条件把握不准致误例3 已知m 、n 是不同的直线，α、β、γ是不同的平面．给出下列命题： ①若α⊥β，α∩β＝m ，n ⊥m ，则n ⊥α，或n ⊥β； ②若α∥β，α∩γ＝m ，β∩γ＝n ，则m ∥n ；③若m 不垂直于α，则m 不可能垂直于α内的无数条直线； ④若α∩β＝m ，n ∥m ，且n ⊄α，n ⊄β，则n ∥α，且n ∥β； ⑤若m 、n 为异面直线，则存在平面α过m 且使n ⊥α. 其中正确的命题序号是________． 找准失分点 ③是错误的；⑤是错误的．1．已知三条不同直线m ，n ，l 与三个不同平面α，β，γ，有下列命题： ①若m ∥α，n ∥α，则m ∥n ； ②若α∥β，l ⊂α，则l ∥β；③α⊥γ，β⊥γ，则α∥β； ④若m ，n 为异面直线，m ⊂α，n ⊂β，m ∥β，n ∥α，则α∥β. 其中正确命题的个数是( ) A ．0 B ．1 C ．2 D ．32．设m ，n 是空间两条直线，α，β是空间两个平面，则下列选项中不正确的是( ) A ．当m ⊂α时，“n ∥α”是“m ∥n ”的必要不充分条件 B ．当m ⊂α时，“m ⊥β”是“α⊥β”的充分不必要条件 C ．当n ⊥α时，“n ⊥β”是“α∥β”成立的充要条件 D ．当m ⊂α时，“n ⊥α”是“m ⊥n ”的充分不必要条件3．一个几何体的三视图如图所示，则该几何体的体积是()A ．64B ．72C ．80D ．1124．如图所示，在正方体ABCD －A 1B 1C 1D 1中，M ，N ，P ，Q 分别是AA 1，A 1D 1，CC 1，BC 的中点，给出以下四个结论：①A 1C ⊥MN ；②A 1C ∥平面MNPQ ；③A 1C 与PM 相交；④NC 与PM 异面．其中不正确的结论是( ) A ．① B ．② C ．③ D ．④5．一个几何体的三视图如图所示，则该几何体的表面积为()A ．2＋ 2B ．3＋ 2C ．1＋2 2D ．56．如图，已知六棱锥P —ABCDEF 的底面是正六边形，P A ⊥平面ABC ，P A ＝2AB ，则下列结论正确的是( )A ．PB ⊥AD B ．平面P AB ⊥平面PBCC ．直线BC ∥平面P AED ．直线PD 与平面ABC 所成的角为45° 7．对于四面体ABCD ，给出下列四个命题：①若AB ＝AC ，BD ＝CD ，则BC ⊥AD ； ②若AB ＝CD ，AC ＝BD ，则BC ⊥AD ； ③若AB ⊥AC ，BD ⊥CD ，则BC ⊥AD ； ④若AB ⊥CD ，AC ⊥BD ，则BC ⊥AD . 其中正确的是________．(填序号)8.如图，四面体ABCD 中，AB ＝1，AD ＝23，BC ＝3，CD ＝2，∠ABC ＝∠DCB ＝π2，则二面角A －BC －D 的大小为________．9．已知直线l ，m ，平面α，β，且l ⊥α，m ⊂β，给出四个命题：①若α∥β，则l ⊥m ；②若l ⊥m ，则α∥β；③若α⊥β，则l ∥m ；④若l ∥m ，则α⊥β. 其中为真命题的是________．(填序号)10．三棱锥D －ABC 及其三视图中的正(主)视图和侧(左)视图如图所示，则棱BD 的长为________．1．43 2．22 3．D 4．相交 5．充分不必要 6．(1)64 (2)24 1．C 2．②③ 3．②④CABCAD 7．①④ 8．π3 9．①④ 10．4 2。

广东省13市2015届高三上学期期末考试数学文试题分类汇编立体几何一、选择题1、（潮州市2015届高三）已知某几何体的三视图如图所示，则该几何体的体积是（）A．B．C．D．2、（东莞市2015届高三）一个侧棱与底面垂直的四棱柱的正视图和俯视图如图所示，该四棱柱的体积为（）A．B．C．D．3、（佛山市2015届高三）在空间中，有如下四个命题：①平行于同一个平面的两条直线是平行直线；②垂直于同一条直线的两个平面是平行平面；③若平面内有不共线的三个点到平面距离相等，则∥；④过平面的一条斜线有且只有一个平面与平面垂直.其中正确的两个命题是( )A．①③B．②④C．①④D．②③4、（广州市2015届高三）用,,表示空间中三条不同的直线, 表示平面, 给出下列命题:①若, , 则∥; ②若∥, ∥, 则∥;③若∥, ∥, 则∥; ④若, , 则∥.其中真命题的序号是A．①②B．②③C．①④D．②④5、（惠州市2015届高三）下列命题正确的是（）A．若两条直线和同一个平面所成的角相等，则这两条直线平行B．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D．若两个平面都垂直于第三个平面，则这两个平面平行6、（江门市2015届高三）某三棱锥的三视图如图1所示，这个三棱锥最长棱的棱长是A．B．C．D．7、（清远市2015届高三）一几何体三视图如图所示，则该几何体的体积是（）A、32－B、32－C、32－D、32－8、（汕头市2015届高三）如图是某几何体的三视图，其中正视图和侧视图是半径为的半圆，俯视图是个圆，则该几何体的全面积为（）A．B．C．D．9、（汕尾市2015届高三）某空间几何体的三视图如图（1）所示，则该几何体的体积为（）A．180 B．144 C．48 D．60www10、（韶关市2015届高三）已知两条直线，两个平面．给出下面四个命题：（）①；②；③；④．其中正确的命题序号为（）A．①②B．②③C．①④D．②④11、（深圳市2015届高三）如图2，三棱锥A－BCD中，AB平面BCD，BCCD，若AB＝BC ＝CD＝2，则该三棱锥的侧视图（投影线平行于BD）的面积为（）A、B、2 C、D、12、（肇庆市2015届高三）设l为直线，a，b是两个不同的平面，下列命题中正确的是A．若l//a，l//b，则a//b B．若a//b，l//a，则l//bC．若l^a，l//b，则a^b D．若a^b，l//a，则l^b13、（珠海市2015届高三）某几何体的三视图如图所示，则其体积为A、B、C、D、14、（惠州市2015届高三）右图是某个四面体的三视图，该四面体的体积为（）A．72 B．36 C．24 D．1215、（汕头市2015届高三）设，是两条不同直线，，是两个不同平面，则下列命题中正确的是（）A．若，，则B．若，，则C．若，，则D．若，，则16、（汕尾市2015届高三）已知直线平面，直线平面，则下列四个结论：①若，则②若，则③若，则④若，则其中正确的结论的序号是（）A.①④B.②④C.①③D.②③17、（肇庆市2015届高三）一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为A．B．C．D．二、解答题1、（潮州市2015届高三）如图，三棱柱中，，，．证明：；若，，求三棱锥的体积．2、（东莞市2015届高三）在如图所示的多面体中，四边形AB1B 1A 和ACC1 A1 都为矩形，AA1 ＝1，AC ＝，AB ＝2，设D ，E 分别是线段BC ，CC 1的中点.(1)若AC ⊥BC ，证明：直线BC ⊥平面ACC1A1；(2)设点M 为线段AB的中点，证明：直线DE // 平面A 1MC ；(3)在（1）条件下，求点D到平面A 1B1 E的距离.3、（佛山市2015届高三）如图,四棱锥,侧面是边长为的正三角形,且与底面垂直,底面是的菱形,为的中点.(Ⅰ) 求证:；(Ⅱ) 在棱上是否存在一点,使得四点共面?若存在,指出点的位置并证明；若不存在,请说明理由；(Ⅲ) 求点到平面的距离.4、（广州市2015届高三）如图3，在多面体中，平面，∥，平面平面，，，．（1）求证：∥；（2）求三棱锥的体积．5、（惠州市2015届高三）如图，在直三棱柱中，，、分别是，的中点．（1）求证：∥平面；（2）求证：平面平面；（3）若，，求三棱锥的体积．6、（江门市2015届高三）如图3，AB是⊙O的直径，PA垂直于⊙O所在的平面，C是圆周上不同于A、B的一点．⑴求证：平面PAC⊥平面PBC；⑵若PA=AB=2，∠ABC=30°，求三棱锥P-ABC的体积．7、（清远市2015届高三）在等腰直角△BCP中，BC=PC=4,∠BCP=90°,A是边BP的中点，现沿CA把△ACP折起，使PB=4，如图1所示.（1）在三棱锥P-ABC中，求证：直线PA⊥平面ABC；（2）在三棱锥P-ABC中，M、N、F分别是PC、BC、AC的中点,Q为MN上任取一点，求证：直线FQ∥平面PAB；8、（汕头市2015届高三）如图，已知平面，四边形为矩形，四边形为直角梯形，，，，．求证：平面；求证：平面；求三棱锥的体积．9、（汕尾市2015届高三）如图（4），在三棱柱中，侧面均为正方形，，点是棱的中点。

2015广东高考理科数学综合小训练（一）1、(2014广东佛山二模,18)如图所示,在正三棱柱(底面是正三角形的直棱柱)A1B1C1-ABC中,M为A1B1的中点,P∈平面ABC,PA⊥平面ACC1A1,且AB=AA1=4,PA=4.(1)求证:C1M⊥平面PCC1;(2)求二面角A1-PC1-C的余弦值.2、(2010福建,17,13分)已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.(1)求椭圆C的方程;(2)是否存在平行于OA的直线l,使得直线l与椭圆C有公共点,且直线OA与l的距离等于4?若存在,求出直线l的方程;若不存在,说明理由.3、(2014广东肇庆一模,20)设双曲线C:-=1(a>0,b>0)的一个焦点坐标为(,0),离心率e=,A、B是双曲线上的两点,AB的中点为M(1,2).(1)求双曲线C的方程;(2)求直线AB的方程;(3)如果线段AB的垂直平分线与双曲线交于C、D两点,那么A、B、C、D四点是否共圆?为什么?4、(2014山东,18,12分)乒乓球台面被球网分隔成甲、乙两部分,如图,甲上有两个不相交的区域A,B,乙被划分为两个不相交的区域C,D,某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在C上记3分,在D上记1分,其他情况记0分.对落点在A上的来球,队员小明回球的落点在C上的概率为,在D上的概率为;对落点在B上的来球,小明回球的落点在C上的概率为,在D上的概率为.假设共有两次来球且落在A,B上各一次,小明的两次回球互不影响.求:(1)小明两次回球的落点中恰有一次的落点在乙上的概率;(2)两次回球结束后,小明得分之和ξ的分布列与数学期望.5、(2014湖南益阳模拟,7)下列有关命题的说法正确的是()A.命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1”B.“x=-1”是“x2-5x-6=0”的必要不充分条件C.命题“若x=y,则sin x=sin y”的逆否命题为真命题D.命题“∃x∈R使得x2+x+1<0”的否定是“∀x∈R均有x2+x+1<0”答案和解析1、[解析]以A为原点,建立空间直角坐标系A-xyz,如图所示,(1分)则P(4,0,0),M(-,1,4),A1(0,0,4),C(0,4,0),C1(0,4,4).(3分)(1)=(-,-3,0),=(0,0,4),=(-4,4,0),因为·=(-)×0+(-3)×0+0×4=0,·=(-)×(-4)+(-3)×4+0×0=0,所以⊥,⊥,即C1M⊥CC1,C1M⊥PC.又CC1∩PC=C,CC1⊂平面PCC1,PC⊂平面PCC1,所以C1M⊥平面PCC1.(6分)(2)=(0,4,0),=(4,0,-4),设平面A1PC1的法向量为n=(x,y,z),则即解得令x=1,得平面A1PC1的一个法向量为n=(1,0,),(10分)由(1)可知平面PC1C的一个法向量为=(-,-3,0),(11分)因为cos<,n>===-,(13分)由图形可知二面角A1-PC1-C为钝角,所以二面角A1-PC1-C的余弦值为-.(14分)2、[解析]解法一:(1)依题意,可设椭圆C的方程为+=1(a>b>0),且可知左焦点为F'(-2,0).从而有解得又a2=b2+c2,所以b2=12,故椭圆C的方程为+=1.(2)假设存在符合题意的直线l,其方程为y=x+t.由得3x2+3tx+t2-12=0.因为直线l与椭圆C有公共点,所以Δ=(3t)2-4×3(t2-12)≥0,解得-4≤t≤4.另一方面,由直线OA与l的距离d=4可得=4,从而t=±2.由于±2∉[-4,4],所以符合题意的直线l不存在.解法二:(1)依题意,可设椭圆C的方程为+=1(a>b>0),且有解得b2=12或b2=-3(舍去).从而a2=16.所以椭圆C的方程为+=1.(2)同解法一.3、[答案]答案见解析[解析](1)依题意得解得a=1.(1分)所以b2=c2-a2=3-1=2,(2分)故双曲线C的方程为x2-=1.(3分)(2)设A(x1,y1),B(x2,y2),则有两式相减得(x1-x2)(x1+x2)=(y1-y2)(y1+y2),(4分)由题意得x1≠x2,x1+x2=2,y1+y2=4,(5分)所以==1,即k AB=1.(6分)故直线AB的方程为y=x+1.(7分)(3)假设A、B、C、D四点共圆.因为AB为圆的弦,所以圆心在AB的垂直平分线CD上,又CD为圆的弦且垂直平分AB,故圆心为CD的中点N.(8分)下面只需证CD的中点N满足|NA|=|NB|=|NC|=|ND|即可.由得A(-1,0),B(3,4).(9分)结合已知条件可得直线CD的方程为y=-x+3,(10分)由得C(-3+2,6-2),D(-3-2,6+2),(11分)所以CD的中点N(-3,6).(12分)因为|NA|==2,|NB|==2,|NC|==2,|ND|==2,(13分)所以|NA|=|NB|=|NC|=|ND|,即A、B、C、D四点在以N(-3,6)为圆心,2为半径的圆上.(14分)4、[解析](1)记A i为事件“小明对落点在A上的来球回球的得分为i分”(i=0,1,3),则P(A3)=,P(A1)=,P(A0)=1--=;记B i为事件“小明对落点在B上的来球回球的得分为i分”(i=0,1,3),则P(B3)=,P(B1)=,P(B0)=1--=.记D为事件“小明两次回球的落点中恰有1次的落点在乙上”.由题意,D=A3B0+A1B0+A0B1+A0B3,由事件的独立性和互斥性,P(D)=P(A3B0+A1B0+A0B1+A0B3)=P(A3B0)+P(A1B0)+P(A0B1)+P(A0B3)=P(A3)P(B0)+P(A1)P(B0)+P(A0)P(B1)+P(A0)P(B3)=×+×+×+×=,所以小明两次回球的落点中恰有1次的落点在乙上的概率为.(2)由题意,随机变量ξ可能的取值为0,1,2,3,4,6,由事件的独立性和互斥性,得P(ξ=0)=P(A0B0)=×=,P(ξ=1)=P(A1B0+A0B1)=P(A1B0)+P(A0B1)=×+×=,P(ξ=2)=P(A1B1)=×=,P(ξ=3)=P(A3B0+A0B3)=P(A3B0)+P(A0B3)=×+×=,P(ξ=4)=P(A3B1+A1B3)=P(A3B1)+P(A1B3)=×+×=,P(ξ=6)=P(A3B3)=×=.可得随机变量ξ的分布列为:P所以数学期望Eξ=0×+1×+2×+3×+4×+6×=.5、[答案] C[解析]否命题应是否定原命题的条件及结论,所以A不正确;由x=-1,可得x2-5x-6=0;反之,由x2-5x-6=0,得到x=-1或x=6,即“x=-1”是“x2-5x-6=0”的充分不必要条件,B不正确;由命题“若x=y,则sin x=sin y”是真命题知其逆否命题也是真命题,C正确;命题“∃x∈R使得x2+x+1<0”的否定应是“∀x∈R均有x2+x+1≥0”,D不正确.故选C.。

2015广东高考理科数学第一轮强化练习Ⅲ（立体几何）1．已知直线m ，n 及平面α，β，则下列命题正确的是（ ）．A ．m ∥α，m ∥β⇒α∥βB ．m ∥α，m ∥n ⇒n ∥αC ．m ⊥α，α⊥β⇒m ∥βD ．m ⊥α，n ∥α⇒m ⊥n2．设点B 是点A （2，－3，5）关于x Oy 面的对称点，则｜AB ｜＝（ ）．A ．10B ．10C ．38D ．383．如果长方体三个面的面积分别是2，3，6，那么它的外接球的半径为（ ）．A ．223B ．6C ． 26D ．34．如图，四棱锥P －ABCD 中，PD ⊥底面ABCD ，ABCD 为正方形，且PD ＝AB ＝1，G 为△ABC 的重心，则PG 与底面所成角的正切值为（ ）．A ．1B ．423C ．322D ．22 5．已知正方体ABCD －A 1B 1C 1D 1的棱长为1，点P 是AA 1的中点，点E 是BB 1上的点，则PE ＋EC 的最小值为（ ）．A ．2B ．215C ．217D ．36．在正方体ABCD －A 1B 1C 1D 1的侧面ABB 1A 1内有一动点P ，它到A 1B 1与BC 的距离之比为2，则动点P 的轨迹为（ ）．A B C D 7．黑白蚂蚁同时从棱长为a 的正方体的顶点A 出发，以相同的速度沿正方体的棱爬行．若黑蚂蚁沿路线AA 1→A 1D 1→…爬行，满足爬行的第i+2段与第i 段互为异面直线；白蚂蚁沿路线AA 1→A 1B 1→…爬行，满足爬行的第i+2段与第i 段互为异面直线，则黑白蚂蚁爬过2004段后彼此相距（ ）．A ．a 2B ．a 3C ．0D ．a 8．已知向量a ＝（2，3，1），b ＝（1，2，m ），且a ⊥b ，则实数m 等于 ．9．将边长为1的正三角形ABC 沿高AD 折叠成直二面角B-AD-C ，则直线AC 与直线AB 所成角的余弦值为 ．10．在长方体ABCD －A 1B 1C 1D 1中，AB=AD=0.5AA 1，点G 为CC 1上的点，且CG=0.25CC 1，则二面角C-AG-D 的余弦值为 ． P G D C B A1 1 1 1。