当前位置：文档之家 › 数学物理方程第三章幂级数展开PPT课件

数学物理方程第三章幂级数展开PPT课件

  • 格式：ppt
  • 大小：1.04 MB
  • 文档页数：42

下载文档原格式

  / 42

合集下载

北京大学数学物理方法经典课件第三章-幂级数展开

北京大学数学物理方法经典课件第三章-幂级数展开

泰勒级数的定义及性质
泰勒级数是幂级数的一种特殊形式，它将函数展开为一系列的非负整数次幂函数的和。泰勒级数在解析学中起 着重要的作用，具有一些重要的性质。
泰勒展开的应用
通过泰勒展开，我们可以将复杂的函数近似为一个多项式，从而简化计算和分析。泰勒展开在数学和物理领域 中有广泛的应用，包括数值计算、数值解微分方程等。
幂级数展开的基本思想和方法
幂级数展开的基本思想是将待展开的函数表示为幂级数的形式，然后通过求 解系数的方式得到展开式。常用的展开方法包括泰勒展开和洛朗展开。
幂级数展开的典型例题
通过具体的例题，我们可以更好地理解和应用幂级数展开。这些例题涉及到各种函数的展开，以及如何利用展 开式求解问题。
幂级数练习题解析
为了加深对幂级数展开的理解提高 解决问题的能力和技巧。
幂级数分析的收敛性问题
在进行幂级数展开时，我们需要考虑展开式的收敛性。这一节将介绍幂级数 在不同区域内的收敛性条件，并给出相应的判别方法。
幂级数收敛半径的计算方法
幂级数的收敛半径是一个重要的概念，它决定了幂级数在哪些点上收敛。我们将介绍几种计算收敛半径的方法， 并通过例题进行实际应用。
经典函数的泰勒级数展开
许多经典函数都可以表示为泰勒级数的形式。在这一节中，我们将重点介绍 几个常见函数的泰勒级数展开，比如指数函数、对数函数、三角函数等。
洛朗级数的定义及性质
洛朗级数是一种特殊的幂级数展开形式，它包含了正幂次和负幂次两部分。 洛朗级数在解析学和复变函数中有重要的应用。
洛朗展开的应用
幂级数展开的误差估计
在实际计算中，我们常常需要估计幂级数展开的误差。这一节将介绍如何使 用剩余项来估计幂级数展开的误差，并给出具体的计算方法。

数学物理方法课件解析函数的幂级数展开

数学物理方法课件解析函数的幂级数展开

幂级数展开求解积分方程
幂级数展开求解积分方程 的步骤
首先将积分方程中的未知函数进行幂级数展 开，然后代入积分方程中求解系数，最后得 到积分方程的解。
举例
求解∫(上限1下限0) (x^2+y^2)^(-3/2) * y dx = 1。将y(x)进行幂级数展开，得到
y(x)=∑(n=0,∞) a_n * x^(n+1)，然后代入 积分方程中求解系数a_n，得到解。
THANKS
感谢观看
幂级数展开的收敛半径
幂级数展开的收敛半径是指函数在一定区间内可以展开成幂 级数的范围。
收敛半径的大小取决于各项系数的变化规律，可以通过比较 相邻项系数的方法来确定收敛半径。
幂级数展开的收敛区间
幂级数展开的收敛区间是指函数可以精确展开成幂级数的区间，通常是一个闭区 间或者半开半闭区间。
在收敛区间内，幂级数展开可以无限逼近原函数，但在收敛区间的外延，误差会 逐渐增大。
数学物理方法课件解析函 数的幂级数展开
• 幂级数展开的概述 • 幂级数展开的原理 • 幂级数展开的应用 • 幂级数展开的实例解析
01
幂级数展开的概述
幂级数展开的定义
幂级数展开是指将一个函数表示为无 穷级数的方式，其中每一项都是该函 数的幂次与系数的乘积。
幂级数展开的一般形式为：$f(x) = a_0 + a_1x + a_2x^2 + cdots + a_nx^n + cdots$，其中 $a_0, a_1, ldots, a_n$ 是常数，$x$ 是自变量。
幂级数展开求解微分方程
幂级数展开求解微分方程的步骤
首先将微分方程中的未知函数进行幂级数展开，然后代入微分方程中求解系数，最后得 到微分方程的解。

高数-幂级数的展开-PPT课件

高数-幂级数的展开-PPT课件

n 1 f n 1 R x x x , 介 x 于 与 x 之 ， 间 n 0 0 n 1 !
——拉格朗日余项
2.级数收敛的必要条件 3.幂级数及其和函数的性质
1
一、泰勒级数 问题：给定函数 f x, 是否能找到一个幂级数，它在某个区间 内收敛，且其和恰好是给定的函数 f x? 若能找到这样的幂级数，则说函数f (x)在该区间内能展开成 幂级数. 泰勒公式： 若函数 f x在 x 0 某邻域内有直到 n1 阶的导数，则 n f x f x 2 n 0 0 (1) f x f x f x x x x x x x R x 0 0 0 0 0 n 2 ! n ! n 1 f n 1 R x x x , 介 x 与 于 x 之 ， 间 n 0 0 n 1 ! ——拉格朗日余项
2 n 0 f x a a x a x a x a 0 f 0 1 2 n 2 n 1 f 0 f x a 2 a x 3 a x na x a 1 1 2 3 n
即
f n 0 n ! a n 1 n n 1 2 a x f x an n n 1 n! n f 0 f 0 2 n f x f 0 f 0 x x x 得证 2 ! n !
问题: （1）x x0 时, 级数(3)是否收敛? （2）若级数(3)收敛, 是否收敛于 f x?
n f x f x 2 n 0 0 x f x 则 f x 设 在 定理 : 在该邻域内能展 f x f x f x x x x x x x 某邻域内有任意阶导数， 0 0 0 0 0 0 2 ! n ! 成泰勒级数(3)的充分必要条件是

chenpc文件数理方法第三章幂级数展开精品文档PPT课件

chenpc文件数理方法第三章幂级数展开精品文档PPT课件

= 2 1 iC R 1 ' f b 1 z 1 b bd 2 1 iC R 2 ' fz b 1 z 1 b bd
CR1' CR2'
::zzbb= bb 2 1 iC R 1 ' f b k 0 z b b k d 2 1 iC R 2 ' f z b k 0 z b b k d
= k 0 2 1 i C R 1 'f b k 1 d z b k k 0 2 1 i C R 2 ' f b k d z b k 1
1、达朗贝尔判别法：
k充 分 大 时 ， w w kk 1q 1 k 1w kz绝 对 收 敛
证明：k N N p 1 w kz= k N N p 1 w 1zq k 1 w 1zq N 1 q q N p N
wkz收敛 k1
wkz绝 对 收 敛 k1
k = N + 1 k = N + 1
1
1
z 1时，zk收敛 k=1
z 1时， zk绝对收敛 k=1
二、绝对收敛性的判别法：
wk z 收敛
k=1
wk z绝对收敛
k=1
Np
Np
wkz wkz
k=N+1
k=N+1
w kz收 敛 w kz绝 对 收 敛
k = 1
k = 1
二、绝对收敛性的判别法：
第三章 幂级数展开
§3.1 幂级数的收敛性
一、基本概念：
N :任意大正整数
不存在 发 散
n
p :任意正整数 ：任意小正数
wk
k1
z
lni m k1wk
z
存
在

函数的幂级数展开(精选)PPT37页

函数的幂级数展开(精选)PPT37页

26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者，好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
函数的幂级数展开（精选）
1、 舟 遥 遥 以 轻飏， 风飘飘 而吹衣 。 2、 秋 菊 有 佳 色，裛 露掇其 英。 3、 日 月 掷 人 去，有 志不获 骋。 4、 未 言 心 相 醉，不 再接杯 酒。 5、 黄 发 垂 髫 ，并怡 然自乐 。 Nhomakorabea▪
谢谢！
37

-幂级数优秀PPT

-幂级数优秀PPT

对端点 x =－1, 级数为 故收敛域为 (1, 1] .
发散 .
收敛;
14
例2. 求下列幂级数的收敛域 :
规定: 0 ! = 1
解: (1)
1
R lim an lim n an1 n
n! 1
(n 1)!
所以收敛域为 ( , ) .
(2) R lim an lim n ! n an1 n (n 1) !
于是存在
常数 M > 0, 使
发散
收敛 发散
收O 敛
发散x
9
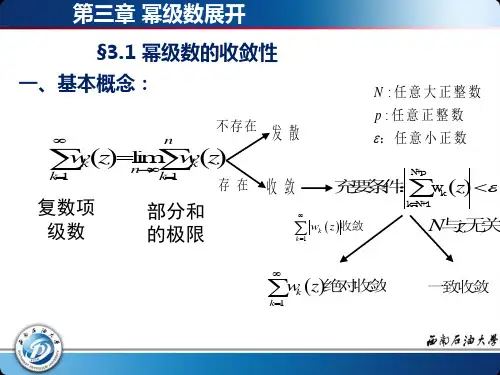
阿贝尔
an xn
an x0n
xn x0n
an x0n
x x0
n
当 x x0 时,
收敛,
也收敛,
故原幂级数绝对收敛 .
反之, 若当 x x0 时该幂级数发散 ,下面用反证法证之.
假设有一点 x1 满足 x1 x0 且使级数收敛 , 则由前 面的证明可知, 级数在点 x0 也应收敛, 与所设矛盾,
求收敛半径时直接用比值法或根值法,
例3
也可通过换元化为标准型再求 .
例4
2. 幂级数的性质
1) 两个幂级数在公共收敛区间内可进行加、减与
乘法运算. 30
常用已知和函数的幂级数
(1) xn
1
;
n0
1 x
(2)
(1)n
n0
x2n
1 1 x2
;
(3)
n0
x2n
1
1 x2
;
(4) xn e x;
n1
n1
记 s( x) n(n 1)xn1 1 x 1
则
n1 x
s1( x) s( x)dx (n 1)xn

数学物理方法课件解析函数的幂级数展开

n 0
1 (l 0, l ) l , R 0, (l ) , (l 0)
3.幂级数的解析性
定理：幂级数 cn ( z a ) n的和函数f ( z )是收敛圆内的一个解析
n 0
函数，且其各阶导数为 f
( p)
( z ) cn n(n 1) (n p 1)( z a ) n p
k 0

在圆 z b z1 b 的外部处处发散.
42
幂级数的收敛圆及其收敛半径
由 Abel 定理及其推论易知，幂级数的收敛区域和发散区 域是不可能相间的。所以对于幂级数 ak ( z b) ，必定
k k 0 k
存在一以 b 为圆心，R 为半径的圆，在圆内该级数绝对 收敛（而且在较小的圆内一致收敛） ，而在圆外发散。这 个圆称为该幂级数的收敛圆，R 称为它的收敛半径。
n
Cn z 称作f ( z )在点的主要部分或无限部分. 而C1
n
1
尤为重要, 称作残数或留数.
定义 : 设为f ( z )的孤立奇点，则 i ) 如果f ( z )在点的主要部分为0，则称为f ( z )的可去奇点. ii) 如果f ( z )在点的主要部分为有限多项，设为 C( m 1) C m C 1 ( z ) m ( z ) ( m 1) z (C m 0)
§3.5 孤立奇点的分类及其性质
若为f ( z )的孤立奇点，则f ( z )在点的某去心邻域K 内可展开成罗朗级数 f ( z)
n n
C z
n

n
其中， Cn z 称作f ( z )在点的正则部分或解析部分.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
z
z0
() a 0 a 1 ( z 0 ) a 2 ( z 0 )2
而
1
1
2i z
有界，
利用柯西公式得
2 1 iC ' ( z )d 2 1 iC 'a 0z0 d 2 1 iC 'a 1 ( z z0 )d 2 1 iC 'a 2 ( z z0 )2 d
a 0 a 1 (z z0 ) a 2 (z z0 )2
Np
k (z1) .
N 1
05.12.2020
N(z2)
阜师院数科院
k (z2) k (z1) k (z2)
3.2 幂级数 幂函数的复变项级数
1. 定义 对于各复常数 z0,a1,a2, ,ak, , 级数
a k ( z z 0 ) k a 0 a 1 ( z z 0 ) a 2 ( z z 0 ) 2 a k ( z z 0 ) k (3.2.1)
故当 z z0 R 当 z z0 R
，(3.2.1) 绝对收敛。 ，(3.2.1) 可能发散。
R 叫收敛半径，以 z 0 为圆心，R 为半径的圆叫
幂级数的 收敛圆
最简单的收敛区域。保证幂级数在圆内的点上绝 对收敛，而在圆外可能发散。圆外仍有区域是收 敛的。
根值判别法
lk i m k ak zz0 1, (3.2.2) 收敛，(3.2.1) 绝对收敛。
lk i m k ak zz0 1, (3.2.2) 发散，(3.2.1) 发散。
05.12.2020
阜师院数科院
故 R lim 1
a k k k
例 (1) 1tt2 tk
解： ak 1
收敛半径:
R lim ak 1 a k
k 1
收敛圆内部为 t 1
其实， tk 1 t t2 tk li1 m tk 1
zz0
1
则实幂级数 (3.2.2) 收敛，且复幂级数 (3.2.1) 绝对 收敛。
3. 收敛圆
记 有 R lim ak
a k k 1
lk im a k a k 1z z z z0 0k k 1lk i a m a kk 1zz0lk i a m a kk 1R 1
05.12.2020
阜师院数科院
柯西判据：复数项级数收敛的充要条件是，
对于一小的正整数 ，必存在一 N 使得
n>N 时有
n p
k ,
k n1
式中 p 为任意正整数。
05.12.2020
阜师院数科院
2. 绝对收敛
k uk2vk2 收敛。
k1
k1
则原级数 k 收敛。 k 1
两个绝对收敛的和，积，仍绝对收敛。
3. 复变项级数
ak (z z0) k
k0
(3.2.2)
满足
lim ak1 a k
k
zz zz0 0kk1lk i m aakk1
zபைடு நூலகம்0
1
则实幂级数 (3.2.2) 收敛，且复幂级数 (3.2.1) 绝对
收敛。 05.12.2020
阜师院数科院
lim ak1 a k
k
zz zz0 0kk1lk i m aakk1
实际上对于 z 1 1 z2 z4 ( 1 )kz2 k 1
1 z2
4. 幂级数的积分表示 利用柯西公式
在一个比收敛圆 C 内稍小的圆 C’ 中幂级数绝对 05.一12.2致020 收敛，故可沿这个阜师圆院数逐科院项积分。
记 C’上点为 ，而C’内任一点为 z，
则圆上的幂级数为
C' C
函数有精确表示和近似表示。 精确表示（解析表示）： 表示为初等函数通过四则运算 近似表示：
逼近 近似表示为初等函数通过四则运算 级数表示 表示为一个函数级数
05.12.2020
阜师院数科院
第三章 幂级数展开
复数项级数；
变项级数（函数级数）；
幂级数；
幂级数对复变函数研究的应用：
泰勒级数；
洛朗级数，函数的奇异性研究。
k(z)1 (z)2 (z) k(z) ,
k 1
的每一项都是复变函数。
实际上，对于 z 的一个确定值，复变项级数变成
一个复数项级数。
05.12.2020
阜师院数科院
复变项级数有一个定义域 B 。它的收敛的概 念应当是相对于这个定义域而言的。
收敛 复变项级数在其定义域 B 中每一点都收 敛，则称在 B 中收敛。
05.12.2020
阜师院数科院
3.1 复数项级数 1. 级数的收敛和柯西判据 级数是无穷项的和
复无穷级数 k 12 k , k 1
每一项为 k ukivk
收敛：
如果极限
收敛 05.12.2020
n
n
n
lim
n k1
kln i m k1ukiln i m k1vk
存在并有限
阜师院数科院
充要条件是其实部与虚部都收敛
绝对一致收敛 在区域 B 中，复数项级数的各项
满足 k(z) mk,
而数项级数 m k k 1
05.12.2020
收敛。 即在各点都绝对收敛
阜师院数科院
给定
N(z1)
Np
k (z1) .
N 1
k (z1)
N(z2)
收敛，但与 z 的位置有关。
N ' p
k (z2 ) .
N '1
N(z1)
k 0
k 1 t
对于 t 1
05.12.2020
tk lim 1tk1 1
k0
k 1t
阜师院数科院
1t
但对于 t 1 显然级数发散。
(2) ( 1 )kz2 k 1 z2 z4 ( 1 )kz2 k k 0
a (1) 解： k
k R lim ak 1 a k
k 1
收敛圆 z 1
k 0
叫以 z 0 为中心的幂级数。
05.12.2020
z0
阜师院数科院
a k ( z z 0 ) k a 0 a 1 ( z z 0 ) a 2 ( z z 0 ) 2 a k ( z z 0 ) k
k 0
2. 收敛的达朗贝尔判据
(3.2.1)
研究(3.2.1) 的 模的如下级数
它满足柯西判据：
复数项级数收敛的充要条件是，对于一小
正整数 ，必存在一 N(z)
使得 n>N(z) 时有
05.12.2020
n p
k (z) ,
k n阜1师院数科院
一致收敛 当 N 与 z 无关时。
即对 B 中所有点 给定 ，就有一个统一的 N
使判据得到满足。
一致收敛的级数的每一项若为连续函数，级 数也将是连续函数。在一条曲线上可以逐项积 分。
05.12.2020
阜师院数科院
又乘以
n!
1
2i ( z)n1
n ! 2iC '(
(z) )k 1 2 n !iC '(