下载文档原格式
离散小波变换(dwt
离散小波变换（Discrete Wavelet Transform，DWT）是一种数学工具，用于信号分析和处理。
它将信号分解成不同的频率子带，可以有效地提取信号的特征。
DWT在许多领域中得到广泛应用，如图像处理、音频编码和生物医学工程等。
离散小波变换使用小波函数对信号进行分解和重构。
小波函数是一种特殊的函数，可以在时域和频域之间进行变换。
DWT将信号分解成低频和高频子带，低频子带包含信号的大部分能量，而高频子带则包含信号的细节信息。
通过多级分解，可以得到不同尺度的子带，从而实现对信号的多层分析。
在DWT中，信号经过分解后，可以进行特征提取、去噪和压缩等操作。
通过对高频子带进行阈值处理，可以实现信号的去噪。
而对低频子带进行压缩，可以减少信号的冗余信息。
DWT还可以用于图像处理中的边缘检测、纹理分析和图像融合等任务。
DWT的优势在于它能够提供多分辨率分析，能够同时捕捉信号的时域和频域特征。
与傅里叶变换相比，DWT可以更好地处理非平稳信号，因为小波函数可以自适应地适应信号的局部特性。
离散小波变换是一种强大的信号分析和处理工具。
它在各个领域中都有广泛的应用，能够提取信号的特征、去除噪声和压缩数据等。
通过合理地使用DWT，可以更好地理解和处理信号，为各种应用提
供支持。
离散小波变换(dwt
离散小波变换（Discrete Wavelet Transform，DWT）是一种常用的信号处理方法，可以将信号在不同尺度上进行分解和重构。
它利用一组基函数，通过对信号进行多尺度分解，提取出信号中的不同频率成分，从而实现信号的特征提取和压缩。
离散小波变换的核心思想是将信号分解为低频和高频部分。
低频部分包含信号中的趋势信息，而高频部分则包含信号中的细节信息。
通过不断进行分解，可以得到不同尺度上的低频和高频部分，从而实现信号的多尺度表示。
离散小波变换具有多尺度、局部性和良好的时频局部性等特点。
它可以有效地处理非平稳信号，对于图像压缩、噪声去除、边缘检测等应用具有重要意义。
离散小波变换的算法基于滤波和下采样操作。
首先，信号经过低通滤波器和高通滤波器，得到低频和高频部分。
然后，低频部分经过下采样操作，得到更低尺度上的低频部分。
这个过程可以迭代地进行，直到达到所需的尺度。
离散小波变换具有很多变种，如离散小波包变换、二维离散小波变换等。
它们在信号处理领域广泛应用，具有很高的实用价值。
总结一下，离散小波变换是一种有效的信号处理方法，可以实现信号的多尺度分解和重构。
它具有多种应用，能够处理非平稳信号并
提取出信号的特征信息。
离散小波变换在图像处理、音频处理、视频压缩等领域有广泛的应用前景。
离散小波变换原理离散小波变换（Discrete Wavelet Transform，DWT）是一种信号分析方法，它将信号分解成不同尺度和频率的子信号。
离散小波变换可以应用于信号处理、图像压缩、声音压缩等领域。
1. 离散小波变换的基本原理离散小波变换是一种多分辨率分析技术，它将信号分解为多个尺度和频率的子信号。
这些子信号可以进一步进行处理或合成为原始信号。
离散小波变换的基本过程是：首先将原始信号通过低通滤波器和高通滤波器进行滤波，并对滤波后的结果进行下采样（即降采样），得到两个子信号——近似系数和细节系数。
然后，对近似系数进行相同的处理，直到得到所需的尺度和频率。
具体地说，假设有一个长度为N的原始信号x[n]，我们要将其分解为J个尺度（scale）和频率（frequency）上不同的子信号。
首先，定义一个长度为L的低通滤波器h[n]和一个长度为H的高通滤波器g[n]，其中L+H=N。
然后，在第j级分解中，将输入信号x[n]分别通过低通滤波器和高通滤波器进行滤波，得到近似系数Aj-1和细节系数Dj-1：Aj-1 = x[n]*h[n]Dj-1 = x[n]*g[n]其中，“*”表示卷积运算。
然后，对近似系数Aj-1进行下采样，得到长度为N/2的新信号：Vj = Aj-1[0], Aj-1[2], ..., Aj-1[N-2]同样地，对细节系数Dj-1也进行下采样，得到长度为N/2的新信号：Wj = Dj-1[0], Dj-1[2], ..., Dj-1[N-2]这样就得到了第j级分解的近似系数Vj和细节系数Wj。
然后，对Vj进行相同的处理，直到得到所需的尺度和频率。
最后，可以将所有尺度和频率上的子信号合成为原始信号x[n]。
具体地说，在第j级合成中，将长度为N/2的近似系数Vj和细节系数Wj上采样（即插值）并通过低通滤波器h[n]和高通滤波器g[n]进行卷积运算，并将结果相加即可：Aj = Vj+1*h[n] + Wj+1*g[n]其中，“+”表示上采样后的加法运算。
第三章 离散小波变换3.1 尺度与位移的离散化方法减小小波变换系数冗余度的做法是将小波基函数⎪⎭⎫ ⎝⎛-=a t a t a τψψτ1)(,的τ,a 限定在一些离散点上取值。
1. 尺度离散化：一种最通常的离散方法就是将尺度按幂级数进行离散化，即取mm a a 0=（m 为整数，10≠a ，一般取20=a ）。
如果采用对数坐标，则尺度a的离散取值如图3.1所示。
图3.1 尺度与位移离散方法2. 位移的离散化：当120==a 时，()τψψτ-=t t a )(,。
（1）通常对τ进行均匀离散取值，以覆盖整个时间轴。
（2）要求采样间隔τ满足Nyquist 采样定理，即采样频率大于该尺度下频率通带的2倍。
3. )(,t a τψ=？当m 增加1时，尺度增加一倍，对应的频带减小一半（见图2.2），可见采样频率可以降低一半，即采样间隔可以增大一倍。
因此，如果尺度0=m 时τ的间隔为s T ，则在尺度为m 2时，间隔可取s m T 2。
此时)(,t a τψ可表示为);(2212221,t T n t T n t n m s m m m s m m ψψψ记作⎪⎭⎫ ⎝⎛⋅-=⎪⎪⎭⎫ ⎝⎛⋅- Z n m ∈, 为简化起见，往往把t 轴用s T 归一化，这样上式就变为()n t t m m n m -=--22)(2,ψψ （3.1）4. 任意函数)(t f 的离散小波变换为⎰⋅=Rn m f dt t t f n m WT )()(),(,ψ （3.2）DWT 与CWT 不同，在尺度—位移相平面上，它对应一些如图3.1所示的离散的点，因此称之为离散小波变换。
将小波变换的连续相平面离散化，显然引出两个问题：（1）离散小波变换>=<)(),(),(,t t f n m W T n m f ψ是否完全表征函数)(t f 的全部信息，或者说，能否从函数的离散小波变换系数重建原函数)(t f 。
（2）是否任意函数)(t f 都可以表示为以)(,t n m ψ为基本单元的加权和∑∈=Zn m n m nm t Ct f ,,,)()(ψ？如果可以，系数n m C ,如何求？上述两个问题可以归结为一个。
长期以来，离散小波变换(Discrete Wavelet Transform)在数字信号处理、石油勘探、地震预报、医学断层诊断、编码理论、量子物理及概率论等领域中都得到了广泛的应用。
各种快速傅氏变换(FFT)和离散小波变换(DWT)算法不断出现，成为数值代数方面最活跃的一个研究领域，而其意义远远超过了算法研究的范围，进而为诸多科技领域的研究打开了一个崭新的局面。
本章分别对FFT 和DWT 的基本算法作了简单介绍，若需在此方面做进一步研究，可参考文献[2]。
1.1 离散小波变换DWT1.1.1 离散小波变换DWT 及其串行算法先对一维小波变换作一简单介绍。
设f (x )为一维输入信号，记)2(2)(2/k x x j j jk -=--φφ，)2(2)(2/k x x j j jk -=--ψψ，这里)(x φ与)(x ψ分别称为定标函数与子波函数，)}({x jk φ与)}({x jk ψ为二个正交基函数的集合。
记P 0f =f ，在第j 级上的一维离散小波变换DWT(Discrete Wavelet Transform)通过正交投影P j f 与Q j f 将P j -1f 分解为：∑∑+=+=-kkjk j k jk j k j j j d c f Q f P f P ψφ1其中：∑=-=-+112)(p n j n k jk c n h c ，∑=-=-+112)(p n j n k j k c n g d )12,...,1,0,,...,2,1(-==j N k L j ，这里，{h (n )}与{g (n )}分别为低通与高通权系数，它们由基函数)}({x jk φ与)}({x jkψ来确定，p 为权系数的长度。
}{0n C 为信号的输入数据，N 为输入信号的长度，L 为所需的级数。
由上式可见，每级一维DWT 与一维卷积计算很相似。
所不同的是：在DWT 中，输出数据下标增加1时，权系数在输入数据的对应点下标增加2，这称为“间隔取样”。
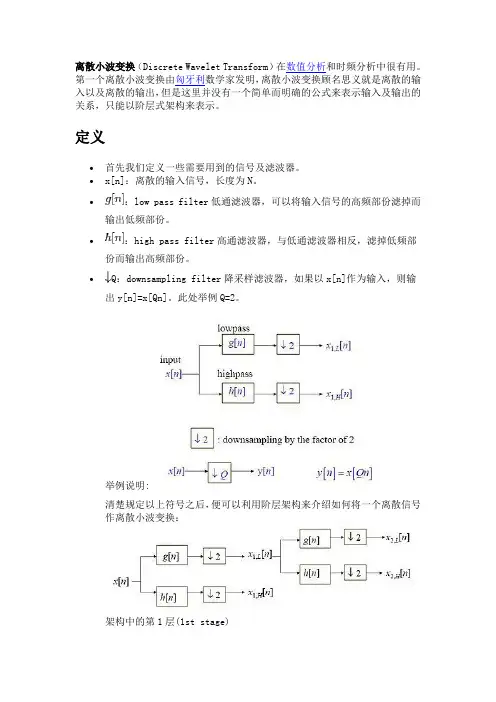
离散小波变换（Discrete Wavelet Transform）在数值分析和时频分析中很有用。
第一个离散小波变换由匈牙利数学家发明，离散小波变换顾名思义就是离散的输入以及离散的输出，但是这里并没有一个简单而明确的公式来表示输入及输出的关系，只能以阶层式架构来表示。
定义∙首先我们定义一些需要用到的信号及滤波器。
∙x[n]：离散的输入信号，长度为N。
∙：low pass filter低通滤波器，可以将输入信号的高频部份滤掉而输出低频部份。
∙：high pass filter高通滤波器，与低通滤波器相反，滤掉低频部份而输出高频部份。
∙Q：downsampling filter降采样滤波器，如果以x[n]作为输入，则输出y[n]=x[Qn]。
此处举例Q=2。
举例说明:清楚规定以上符号之后，便可以利用阶层架构来介绍如何将一个离散信号作离散小波变换：架构中的第1层(1st stage)架构中的第2层(2nd stage)可继续延伸架构中的第层( stage)则第的长度为二维离散小波转换此时的输入信号变成，而转换过程变得更复杂，说明如下：首先对n方向作高通、低通以及降频的处理接着对与延著m方向作高低通及降频动作经过(1)(2)两个步骤才算完成2-D DWT的一个stage。
[编辑]实际范例以下根据上述2-D DWT的步骤，对一张影像作二维离散小波变换(2D Discrete Wavelet Transform)原始影像2D DWT的结果[编辑]复杂度(Complexity)在讨论复杂度之前，先做一些定义，当x[n]*y[n]时，x[n]之长度为N，y[n]之长度为L：其中，为(N+L-1)点离散傅里叶反转换(inverse discrete Fourier transform)为(N+L-1)点离散傅里叶转换(discrete Fourier transform)(1)一维离散小波变换之复杂度(没有分段卷积(sectioned convolution))：(2)当 N >>> L 时，使用“分段卷积(sectioned convolution)”的技巧：将x[n]切成很多段，每段长度为，总共会有段，其中。
