一维无限深势阱 (2)

格式：doc
大小：60.00 KB
文档页数：4

下载文档原格式

一维无限深势阱 (2)

论文题目：一维无限深势阱简述制作人：刘子毅（应用物理（1））学号：09510113一维无限深势阱一、引言Hu = Eu,,2222Eu Vu dxu d m =+- (1) 在图中Ⅰ区，-a/2<x<a/2,式中的V=0；在图中Ⅱ区，x<-a/2和x>a/2, V=∞. 现在解Ⅰ区情况的方程，V=0，（1）式成为.2,22222mEk u k u mE dx u d =-=-= 设axe u =，那么u a u n2=，代入上式，u k u a 22-= ik a ±=所以ikx ikx Be Ae u -++=kx D kx C u sin cos += （2）（2）式是Ⅰ区的通解。

2、一维无限深阱电子的基态222222282n mdh n md E n == π n=1、2、3…… 无量纲处理：以波尔半径2200m e a ε=里德伯20242ε me R y =分别为长度和能量单位能量可化为21d E π3、数值模拟当n=1时，1E 和d 的一组数值用计算机编程模拟如下：设d 从0.3 3.0 include ‹stdio.h › include ‹math.h ›main() { double e,d,c; int i; c=3.14,d=0.3; for(i=0;i ‹10;i++) { e=c/(d*d); printf(“%lf ”，&e)； d=d+0.3;} }d 的取值利用画图软件描绘出横坐标为d ，纵坐标为E 的曲线设d 从0.3 3.0，能量化简为：21dE π=模拟如下：。

高二物理竞赛课件一维无限深势阱

满足归一化条件,另外
z
和
1 me
z
z
还要满足边界条件.
有限深势阱能带
有限
无限
有效质量
En k
E n,0
2k 2 2m 0
2
m
2 0
nn
un0 k p un0 2 En0 En0
E n,0
2k 2
2
1
m
0
m 022k2
nn
un0
k
p
un0
En0 En0
2
E n,0
2k 2 2me
2 2
z
1
me z z
nz
zV
z nz
z
Enz
nz
z,
波函数形式为
B expz,z lz 2
nz
Acoskz, lz A sinkz, lz
B exp z
2
2
,
z z z
lz
lz lz 2
2 2
其中 k
2meI Enz 2
,
2meII V0 Enz 2
,
nz z
一维无限深势阱
一维无限深势阱
E nz
2 2 2me ,hLz2
nz2 ,nz
1,2,3,
有限深真实势阱,仅存在着几个束缚态，
E nz nz2, 系数变小,能级降低.这是由于
势垒降低,电子产生贯穿（Δx↑→ Δ p↓
→ p↓）.当 lz 0,Enz (发散)电子态接近于势垒中的布洛赫态.
.
1
me1m0 Nhomakorabeam 022k2
nn
un0 k p un0 En0 En0

16-3一维势阱和势垒问题解读

n4
x a
a x
第k激发态(n=k+1)有k个节点。
（2）一维无限深势阱的粒子位置概率密度分布
1
2
n 1
0 2 2 n 2 a
2
x
0 无数峰：量子经典均匀分布 0
a a n 1，x 处，几率最大 0 3 2 b n ，峰数，当n 时，
4
U0
II
III
o
a
x
而在微观粒子的情形，却会发生反射。
ቤተ መጻሕፍቲ ባይዱ
（2）E<U0 从解薛定谔方程的结果来看，在势垒内部存在波函数2。即在势垒内部找出粒子的概率不为零，同时，在 x>a区域也存在波函数，所以粒子还 I 可能穿过势垒进入x>a区域。
V
V0
II
III
o
a
x
粒子在总能量E小于势垒高度时仍能贯穿势垒的现象称为隧道效应。
式中 A和α是待定常数，由边界条件和归一化条件确定。
( x) A sin( kx )
从物理上考虑，粒子不可能透过阱壁，因而按照波函数的统计诠释，要求在阱壁上和阱外波函数为0。考虑波函数在阱壁上等于零的情况，即
(0) 0, (a) 0
————边界条件
(0) 0
这说明：并非任何 E值所对应的波函数都能满足一维无限深方势阱所要求的边界条件，只有当能量取上式给出的那些分立的值 En（体系的能量本征值）时，相应的波函数才是物理上有意义的，即本问题中体系的能量是量子化的，亦即体系的能谱是分立的。
2
2
2 2 2
( x) A sin kx
nx n ( x) A sin( ) a

2无限深势阱

是奇函数
(odd function)
l =1 时， = /2，e Acos kx
是偶函数
(even function)
l 为其他整数值时，给出相同结果
（可能差正负号，但不影响| |2 ）
由 o (a / 2) Asin(ka / 2) 0
ka n , n 2，4，6，
一维无限深方形势阱中的波函数与能量
U(x)
U(x)
U=U0
U=U0
U→∞
U→∞
E
极
U=0 限
0
x
金属
a
E
U=0
a /2 0 a /2 x
无限深方势阱（potential well）
x a / 2 U( x) ， 0
x

a / 2 U(x)

0 ，Hˆ

2 2m
d2 d x2
a
所以有能量本征函数：
on
a sin n x 2a
en
a n cos x
2a
0
xa 2
x a 2
（2）全部波函数
考虑振动因子有
n
(
x,
t
)

n
(
x)

e
i
Ent
“能量本征波函数”，“能量本征态”
（3）概率密度：|n( x, t) |2 |n( x) |2
无限深方势阱中的粒子
定态薛定谔方程
[
2
2
U (r )] (r )
E (r )
2m
从数学上来讲：E 不论为何值该方程都有解从物理上来讲： E只有取某些特定值，该方

量子力学一维势阱

III
(x)
2
2
(U
E )
III
(x)
0
xa
方程可简化为：
d2
dx
2
I
2 I
0
d2
dx
2
II
2 II
0
d2
dx
2
III
2 III
0
U(x)
I
II
-a 0
III a
U(x)
I
II
-a 0
III
a
1 单值，成立； 2 有限：
当x - ∞ ， ψ 有限条件要求
C2=0。
d2
(x)
2
2
[U ( x)
E ]
(x)
0
β2
势V(x)分为三个区域，用 I 、II 和 III 表达，其上旳波函数分别为 ψI(x),ψII(x) 和 ψIII (x)。则方程为：
d2
dx 2
I
(x)
2
2
(U
E )
I
(x)
0
x a
d2 dx 2
II
(x)
2
2
E
II
(x)
0
a xa
d2
dx 2
(r , t) (r , t)
称波函数具有偶宇称；
(r , t) (r , t)
称波函数具有奇宇称；
（3）假如在空间反射下，
(r , t) (r , t)
则波函数没有拟定旳宇称
（四）讨论
一维无限深势阱中粒子旳状态
（1）n = 1, 基态，
0
n
1
n
sin

2.6 一微无限深势阱

由归一化条件

a
0
( x, t ) dx ( x) dx
0
2
a
2

可得 A 2 a
a
0
n A sin x dx 1 a
2
0 x 0, x a n ( x) n 1,2, n 2 a sin a x 0 x a
2mE k 2
a a
m n m n m n 1 sin x sin x cos x cos x a a 2 a a
可得若
a 2

a
0
m n dx 0
mn
2
a 1 n 2n 2 A sin xdx A 1 cos x dx 0 0 2 a a 1 A2 a 2
x
所以,系数A必须为零,则Байду номын сангаас由于
e x
x

当
Be e
x
x0

0
所以,系数B必须为零,则
d ( x) E ( x) 阱内 2 2m dx
2
令
k 2mE
2
2
2
d ( x) 2 k ( x) 0 2 dx
其通解为 ( x) Asin kx
a
| ( x) | dx 1
2
1 , a
（与n无关）
最后，波函数是：
1 n n (x) sin ( x a ). 2a a
A和为待定常数
根据波函数的连续、单值的条件有
(0) 0 0

sin ka 0
0

16-3 一维势阱和势垒问题

ψ(x) = Asinkx
nπx ψn(x) = Asin ( ) a
ka = nπ , n = 1,2,3,......
(0< x < a) n =12,3 , ,...
与能量本征值E 与能量本征值 n相对应的本征波函数ψn (x)为：
利用归一化条件
∫
2
ψn(x) dx = ∫ ψn(x) dx =1 0 −∞
ψ2 =0
理由:因为势壁无限高所以粒子不能穿透势壁理由因为势壁无限高,所以粒子不能穿透势壁故势因为势壁无限高所以粒子不能穿透势壁,故势阱外的波函数为零
定态薛定谔方程为
d ψ 2µ E + 2 ψ =0 2 dx ℏ
2
E是粒子的总能量，E > 0，令是粒子的总能量，是粒子的总能量，定态薛定谔方程变为
ℏ
V
U0
0≤ x≤a
I II III
O a
x
ℏ
d2ψ1(x) 2 + k ψ1(x) = 0, x ≤0 2 dx 三个区间的薛定 2 谔方程简化为：谔方程简化为： d ψ 2 ( x) − γ 2ψ ( x) = 0, 0≤ x≤a 2 2 dx d 2ψ3 (x) 2 + k ψ3 (x) = 0, x≥a 2 dx
一维无限深方势阱的数学表达形式：
U (x ) =
0
(0 < x < a )
∞ ( x ≤ 0 及x ≥ a )
一维无限深方势阱的图形表达形式： ∞
U(x)
∞ 粒子只能在宽为 a 的两个无限高势壁间运动，限高势壁间运动，这种势称为一维无限深方势阱。
0
a
x
因为系统的势能与时间无关，因为系统的势能与时间无关，因此这是一个定态问题，可以用定态薛定谔方程进行求解。态问题，可以用定态薛定谔方程进行求解。

一维无限深势阱ppt课件

n个节点。
四.几率分布:
在经典力学中,在ξ到ξ+dξ之间的区域内找到质点的 11
几率ω (ξ) dξ与质点在此区域内逗留的时间dt成
比例:
( )d dt
T
T是振动周期。因此有
( )
T
1
d
dt
1 vt
即几率密度与质点的速度成反比。对于经典的线性谐振子，ξ= a sin(ωt+δ ) ,在ξ点的速度为
J
i
2
[
i
d dx
* i
* i
d dx
i
]
k1
|
A |2
JD
k1
| c |2 ,
JR
k1
|
A |2
16
透射系数与反射系数为：
D
JD J
(k12
4k12k22 k22 )2 sin 2 k2a 4k12k22
R
JR J
(k12
(k12 k22 )2 sin 2 k2a k22 )2 sin 2 k2a 4k12k22
13
如果将此问题推广到三维，显然它是散射问题。
二、方势垒的穿透 (1)E>U0 的情况：
薛定谔方程为
d 2
dx 2
2
2
(E
U
0
)
0
令 k1 2E / 2
则其解为
k2 2 (E U 0 ) / 2
1 Aeik1x Ae ik1x
x0
2 Beik2x Beik2x 0 x a
3 Ceik1x C e ik1x
数为：
2 2[U ( x)E ]dx
D D0e
贯穿势垒U(x)的透射系数应等于贯穿所有这些方形势垒的透射系数之积，即

一维无限深势阱薛定谔方程求解

一维无限深势阱薛定谔方程求解一维无限深势阱是量子力学中最经典的问题之一，其求解对于理解基本的量子力学原理以及波函数的性质具有重要的意义。

薛定谔方程是描述量子力学体系中粒子的行为的基本方程，通过求解薛定谔方程，我们可以获得系统的波函数及其相应的能级。

让我们来考虑一个无限深势阱，这个系统可以简单地用一个势能函数来描述。

在这个系统中，粒子只能在一个有限的空间区域内运动，而且势能在这个区域内是常数为零的。

首先，我们需要写出薛定谔方程。

对于一维情况，薛定谔方程可以写成：-ħ²/2m * d²ψ(x)/dx²+ V(x)ψ(x) = Eψ(x)。

其中，ψ(x)是系统的波函数，V(x)是势能函数，E是波函数对应的能量。

对于无限深势阱，势能函数在阱内为零，在阱外为无穷大。

因此，V(x)在阱外的值可以视为一个很大的正数。

接下来，我们需要考虑边界条件。

在无限深势阱中，粒子是被约束在一个有限空间内的。

因此，在边界处，粒子的波函数必须为零。

对于一个无限深势阱，边界条件可以写为ψ(0)=ψ(a)=0，其中，a是阱的宽度。

现在，让我们尝试求解薛定谔方程。

由于系统的势能在阱内为零，薛定谔方程可以简化为：-d²ψ(x)/dx² = k²ψ(x)，其中，k=√(2mE/ħ²)。

这是一个常微分方程，我们可以通过分离变量和积分来求解。

假设ψ(x)可以分解为两个函数的乘积：ψ(x) = X(x)Y(y)。

将这个假设代入方程中，并整理得：1/X(x) * d²X(x)/dx² = -1/Y(y) * dY(y)/dy = -k²。

我们可以分别对X(x)和Y(y)进行求解，然后将两个解再组合起来得到系统的波函数。

针对常微分方程1/X(x) * d²X(x)/dx² = -k²，我们可以得到其解为X(x) = Asin(kx) + Bcos(kx)，其中，A和B是常数。

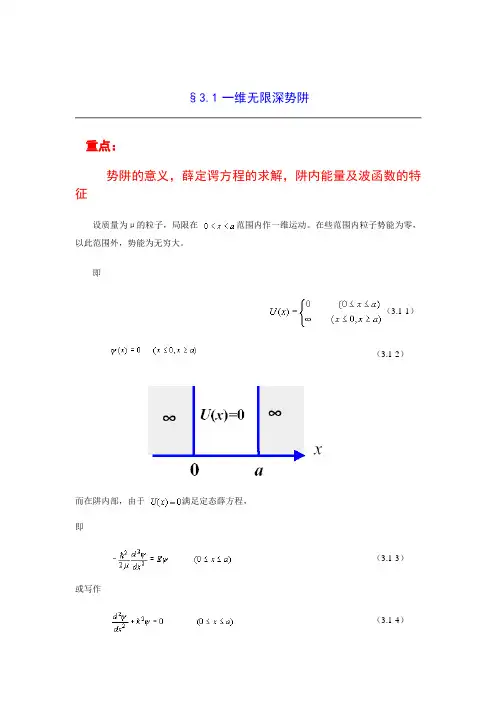
§3.1一维无限深势阱

§3.1 一维无限深势阱重点：势阱的意义，薛定谔方程的求解，阱内能量及波函数的特征设质量为μ的粒子，局限在范围内作一维运动。

在些范围内粒子势能为零，以此范围外，势能为无穷大。

即（3.1-1）（3.1-2）满足定态薛方程，而在阱内部，由于即（3.1-3）或写作（3.1-4）其中（3.1-5）常系数二阶微分方程（3.1-4）的通解为（3.1-6）为待定常数，合并（3.1-2）,（3.1-6）式得（3.1-7）和处，必须为零，由于波涵数在势阱边界上发须为连续的条件，所以在即，（3.1-8）（3.1-9）这就是解方程（3.1-4）时需要用到的边界条件。

由（3.1-8）式，则式（3.1-6）为到处为零，这在物理上是没有意义的，不能为零，否则所以必须这样就有（3.1-10）再利用条件（3.1-9）得因而必须满足下面条件（3.1-11）给出被函数无物理意义，而取负数时给不出新的波函数）。

（将（3.1-11）式代入（3.1-5）式得到体系的能量（3.1-12）由此可见，粒子束缚在势阱中时，能量只能取一系列分立的数值，即它的能量是量子化的。

的粒子将（3.1-11）式代入（3.1-10）式，并重写（3.1-7）式，我们就得到能量为有波函数（3.1-13）应用归一化条件（3.1-14）可求得的粒子的归一化波函数为这样，最后得到能量为（3.1-15）一维无限深势阱中粒子的定态波函数是（3.1-16）利用公式我们可以把定态波函数写成（3.1-17）是由两个沿相反方向上式与弦振动的驻波函数形式相同。

由此可见定态波函数传播的平面波迭加而成的驻波。

下面讨论几个问题，并与宏观粒子作比较。

（1）束缚态和基态在时，波函数，粒子被束缚于阱内，故通常把无穷远处为零的波函数所描写的状态称为束缚状态，一般来说，束缚态的能级是分立的。

体系最低能量的态称为基态，在一维无限深势阱中的基态是的基本征态。

这与经典理论结果完全不同，经典理论认为粒子最低能量必须为零。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

论文题目：一维无限深势阱简述
制作人：刘子毅（应用物理（1））
学号：09510113
一维无限深势阱
一、引言
Hu = Eu,
,2222Eu Vu dx
u d m =+- (1) 在图中Ⅰ区，-a/2<x<a/2,式中的V=0；在图中Ⅱ区，x<-a/2和x>a/2, V=∞. 现在解Ⅰ区情况的方程，V=0，（1）式成为
.2,22
2
22
mE
k u k u mE dx u d =-=-= 设ax
e u =，那么u a u n
2
=，代入上式，
u k u a 22-= ik a ±=
所以
ikx ikx Be Ae u -++=
kx D kx C u sin cos += （2）
（2）式是Ⅰ区的通解。

2、一维无限深阱电子的基态
2
2
22
22
282n md
h n md E n == π n=1、2、3…… 无量纲处理：以波尔半径2
2
00m e a ε=
里德伯2024
2ε me R y =分别为长度和能量单位
能量可化为2
1
d E π
3、数值模拟
当n=1时，1E 和d 的一组数值用计算机编程模拟如下：设d 从0.3 3.0 include ‹stdio.h › include ‹math.h ›
main() { double e,d,c; int i; c=3.14,d=0.3; for(i=0;i ‹10;i++) { e=c/(d*d); printf(“%lf ”，&e)； d=d+0.3;} }
d 的取值利用画图软件描绘出横坐标为d ，纵坐标为E 的曲线设d 从0.3 3.0，能量化简为：2
1d
E π
=
模拟如下：。

一维无限深势阱 (2)

合集下载